基礎圖論
Graph Theory
author: __Shioko
先備知識
- C++基本語法
- C++ STL
- 遞迴
- 複雜度估計
- Disjoint-Set
- 數學歸納法(?
圖論在研究什麼?
研究名叫"圖"的結構
而圖是由點集和邊集所構成的
點(vertex)
代表事物
邊(edge)
代表事物之間的關係

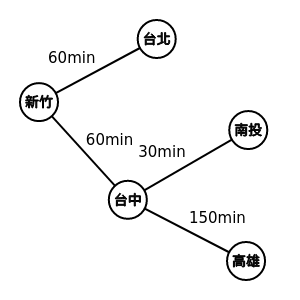
例子-交通圖
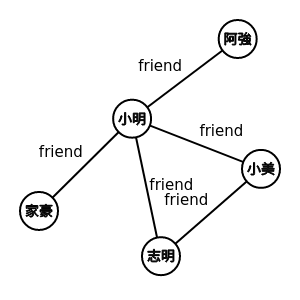
例子-朋友關係圖
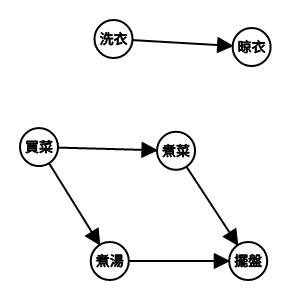
例子-流程圖
基本定義/名詞
邊的種類
無向邊
undirected edge
(u, v) = (v, u)
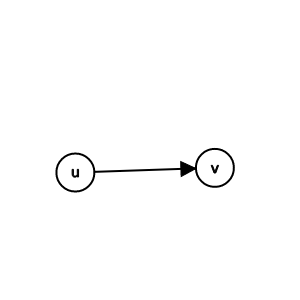
有向邊
directed edge
(u, v) != (v, u)
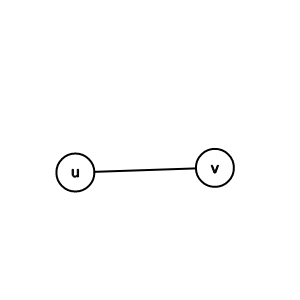
無向圖(undirected graph)
只有無向邊的圖
有向圖(directed graph)
只有有向邊的圖
混合圖(mixed graph)
同時有有向/無向邊的圖
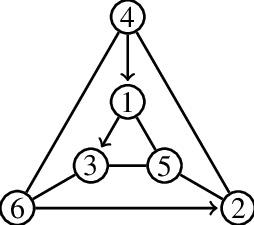
相鄰(adjacent)
在無向圖中
如果存在邊E(u, v)
我們就稱節點u和節點v相鄰
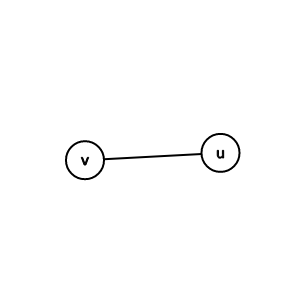
點度(degree)
在無向圖中
一個節點v的點度為和v相連的邊數
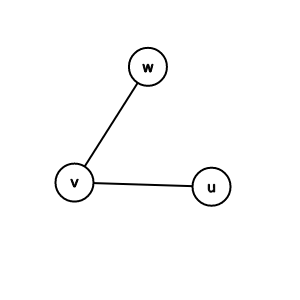
v的點度: 2
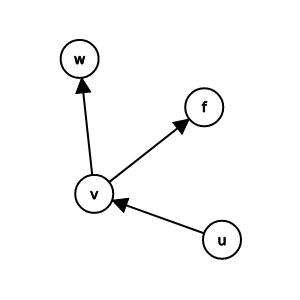
入度(indegree)/
出度(outdegree)
在有向圖中又可以分成入度和出度
v的入度: 指出v的邊數
v的出度: 指到v的邊數
v的入度: 1, v的出度: 2
邊權(weight)
有時候邊可以帶有一些數字
稱為邊權
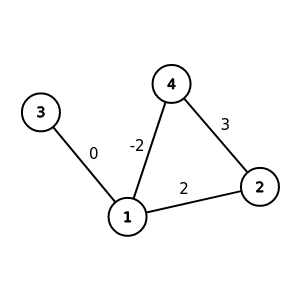
帶權圖(weighted graph)
當圖上的邊有邊權時
這個圖就稱為帶權圖

無權圖(unweighted graph)
當圖上的邊沒有邊權時
這個圖就稱為無權圖
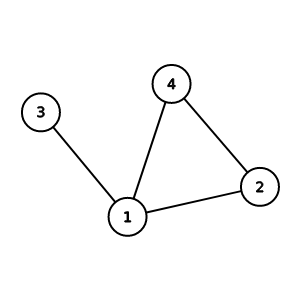
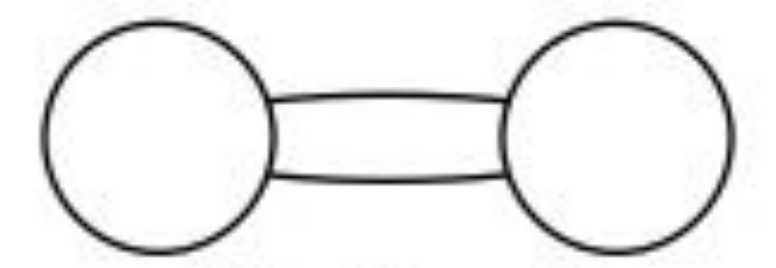
重邊(multiple edge)
當兩個節點u, v之間有多於一條邊時
就稱為重邊
路徑(path)
當我們從節點u沿著邊隨便走到v
則途中經過的節點構成的序列就稱為路徑
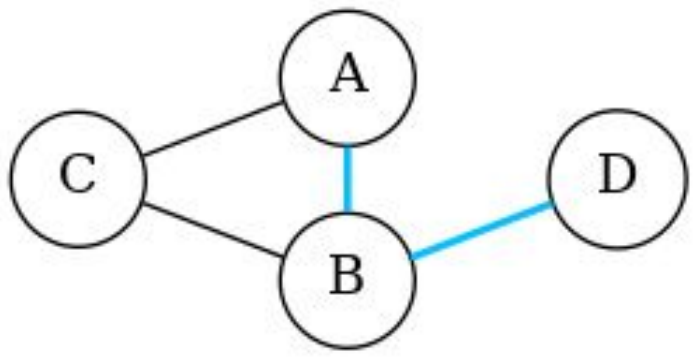
一條A到D的路徑(A, B, D)
簡單路徑(simple path)
當路徑上經過的點不重複時
就稱為簡單路徑

路徑(A, B, D)是簡單路徑
路徑(B, A, C, B, D)不是簡單路徑
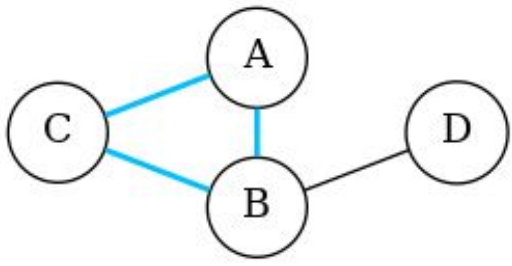
環(cycle)
當路徑只有起點和終點一樣且不走同一條邊時
就稱為環
路徑(A, B, C, A)是一個環
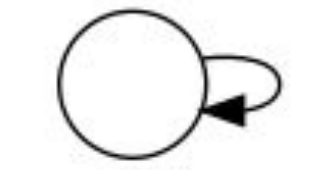
自環(loop)
當一條邊連向自己時
就稱為自環
連通(connect)
當節點u, v之間存在路徑時
我們就稱u和v連通
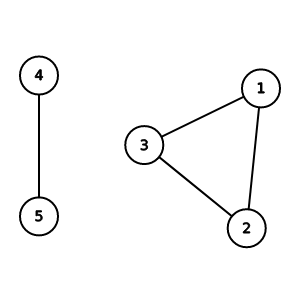
(4, 5)連通, (1, 2, 3)連通
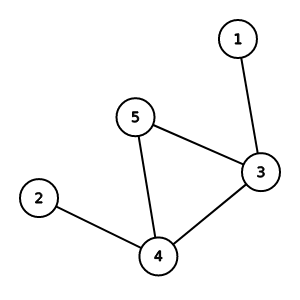
連通塊(connected component)
滿足點集內所有點互相連通的最大點集
稱為連通塊

(4, 5)是一個連通塊, (1, 2, 3)是一個連通塊
簡單圖(simple graph)
當一個圖沒有重邊和自環時
就稱為簡單圖
子圖(subgraph)
把一個圖G(V, E)拔掉一些點和邊
且剩餘的邊的端點都還在圖上
產生的新圖G'就稱為G的子圖

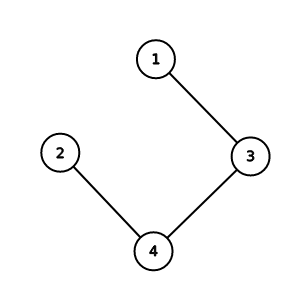
原圖 子圖
圖的儲存方式
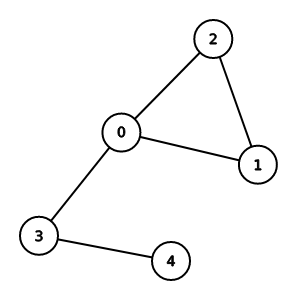
鄰接矩陣(adjacency matrix)
對於一個V個節點的圖
開一個V * V的布林陣列G[V][V]
G[i][j]為true代表有一條邊連接i和j, 反之
| G | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | F | T | T | T | F |
| 1 | T | F | T | F | F |
| 2 | T | T | F | F | F |
| 3 | T | F | F | F | T |
| 4 | F | F | F | T | F |
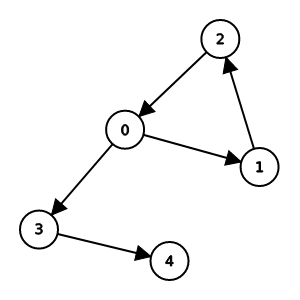
有向圖的狀況
G[i][j] = true代表有邊從i連到j
G[j][i] = true代表有邊從j連到i
| G | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | F | T | F | T | F |
| 1 | F | F | T | F | F |
| 2 | T | F | F | F | F |
| 3 | F | F | F | F | T |
| 4 | F | F | F | F | F |
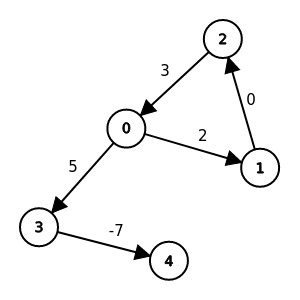
帶權圖的狀況
開一個V * V的整數陣列G[V][V]
G[i][j] = INF的時候代表沒有邊
G[i][j] != INF時代表有條邊權G[i][j]的邊從i連到j
| G | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | INF | 2 | INF | 5 | INF |
| 1 | INF | INF | 0 | INF | INF |
| 2 | 3 | INF | INF | INF | INF |
| 3 | INF | INF | INF | INF | -7 |
| 4 | INF | INF | INF | INF | INF |
實作
const int V = 2000;
bool G[V][V];
void addEdge(int u, int v) {
G[u][v] = G[v][u] = true;
}
void deleteEdge(int u, int v) {
G[u][v] = G[v][u] = false;
}
bool findEdge(int u, int v) {
return G[u][v];
}複雜度
增加一條邊: O(1)
刪除一條邊: O(1)
查詢(i, j)之間是否有邊: O(1)
空間複雜度: O(V^2)
鄰接串列(adjacency list)
對於一個V個節點的圖
開V個整數動態陣列G[V]
當(i, j)之間有邊時
陣列G[i]會有元素j, 陣列G[j]會有元素i
| G | |
|---|---|
| 0 | 1, 2, 3 |
| 1 | 0, 2 |
| 2 | 0, 1 |
| 3 | 0, 4 |
| 4 | 3 |

有向圖的狀況
當有邊從i連到j時
陣列G[i]會有元素j

| G | |
|---|---|
| 0 | 1, 3 |
| 1 | 2 |
| 2 | 0 |
| 3 | 4 |
| 4 |
帶權圖的狀況
對於一個V個節點的圖
開V個存pair<int, int>的動態陣列G[V]
當(i, j)之間有邊權w的邊時
陣列G[i]會有元素(j, w)

| G | |
|---|---|
| 0 | (1, 2), (3, 5) |
| 1 | (2, 0) |
| 2 | (0, 3) |
| 3 | (4, -7) |
| 4 |
實作
const int V = 200000;
vector<int> G[V];
void addEdge(int u, int v) {
G[u].push_back(v);
G[v].push_back(u);
}
void deleteEdge(int u, int v) {
for(int i = 0; i < G[u].size(); i++) {
if (G[u][i] == v) {
G[u].erase(&G[u][i]);
break;
}
}
}
bool findEdge(int u, int v) {
for(int i = 0; i < G[u].size(); i++) {
if (G[u][i] == v)
return true;
}
return false;
}複雜度
增加一條邊: O(1)
刪除一條邊: O(E)
查詢(i, j)之間是否有邊: O(E)
空間複雜度: O(V + E)
鄰接串列
增加一條邊: O(1)
刪除一條邊: O(E)
查詢(i, j)之間是否有邊: O(E)
空間複雜度: O(V + E)
鄰接矩陣
增加一條邊: O(1)
刪除一條邊: O(1)
查詢(i, j)之間是否有邊: O(1)
空間複雜度: O(V^2)
複雜度比較
鄰接串列
增加一條邊: O(1)
刪除一條邊: O(E)
查詢(i, j)之間是否有邊: O(E)
空間複雜度: O(V + E)
鄰接矩陣
增加一條邊: O(1)
刪除一條邊: O(1)
查詢(i, j)之間是否有邊: O(1)
空間複雜度: O(V^2)
複雜度比較
可以發現鄰接矩陣除了耗費空間以外
操作的速度都很快 適合點數少的圖
而鄰接串列比較適合點數多的圖
圖的遍歷方式
深度優先搜尋
Depth-First Search
深度優先搜尋
從一個節點開始 先看到的路先走
直到沒有路可以走之後再退回去找其他路
遍歷的時候同時記錄哪些節點走過
以免走到重複的節點
過程
電腦畫圖不好畫 還是用白板吧┐(´д`)┌
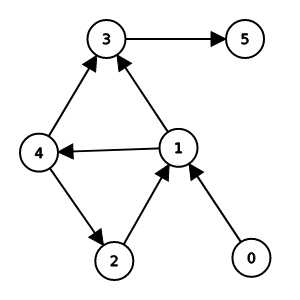
實作
const int V = 200000;
vector<int> G[V];
bool vis[V];
void DFS(int now) {
vis[now] = true;
for(int i = 0; i < G[now].size(); i++) {
if (!vis[G[now][i]])
DFS(G[now][i]);
}
}const int V = 200000;
vector<int> G[V];
bool vis[V];
void DFS(int now) {
vis[now] = true;
for(int X : G[now]) {
if (!vis[X])
DFS(X);
}
}複雜度
由於每個節點都會被走過一次
每條邊也都會被看過一次
時間複雜度為O(V + E)
應用-找連通塊數量
由於每次DFS都會走過一個連通塊的所有節點
所以只要對每個沒走過的節點DFS
並計算DFS的次數
就可以知道一張圖的連通塊數量
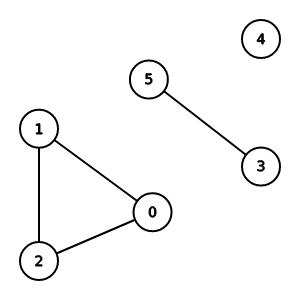
CSES-Building Roads
位元國有n個城市及m條雙向道路
你的任務是在一些城市之間建造道路
使任兩個城市都存在到對方的路徑
請你找出最少需要蓋幾條路才能滿足上述條件
且這些路應該要蓋在哪些節點之間
link: https://cses.fi/problemset/task/1666/
CSES-Building Roads
首先 蓋邊(i, j)可以分成兩種情況:
1. i和j原本在同一個連通塊, 連通塊數量不變
2. i和j原本不在同一個連通塊, 連通塊減少一個
CSES-Building Roads
首先 蓋邊(i, j)可以分成兩種情況:
1. i和j原本在同一個連通塊, 連通塊數量不變
2. i和j原本不在同一個連通塊, 連通塊減少一個
所以需要蓋的邊數會是原圖的連通塊數量 - 1
且這些邊都是不同連通塊的隨便一個點
廣度優先搜尋
Breadth-First Search
廣度優先搜尋
從一個源點S開始
掃過所有與S相鄰的點 加入待尋訪的清單
再依序走訪清單上的點 掃過所有與它相鄰的點...
換種角度看的話就是以源點為起點
依序尋訪距源點1的點, 距離源點2的點...
過程
白板again!
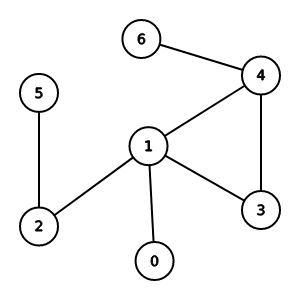
實作
const int V = 200000;
vector<int> G[V];
int dis[V];
queue<int> q;
void BFS(int S) {
for(int i = 0; i < V; i++)
dis[i] = -1;
q.push(S);
dis[S] = 0;
while(!q.empty()) {
int now = q.front();
q.pop();
for(int i = 0; i < G[now].size(); i++) {
if (dis[G[now][i]] == -1) {
dis[G[now][i]] = dis[now] + 1;
q.push(G[now][i]);
}
}
}
}const int V = 200000;
vector<int> G[V];
int dis[V];
queue<int> q;
void BFS(int S) {
for(int i = 0; i < V; i++)
dis[i] = -1;
q.push(S);
dis[S] = 0;
while(!q.empty()) {
int now = q.front();
q.pop();
for(int X : G[now]) {
if (vis[X] == -1) {
dis[X] = dis[now] + 1;
q.push(X);
}
}
}
}複雜度
同樣的分析
執行BFS時每個節點都會被看過一次
每條邊也都會被看過一次
複雜度O(V + E)
應用-無權圖單點源最短路徑
剛才提到BFS其實就是
依照離源點距離由近到遠進行尋訪
因此在無權圖上可以用BFS尋找每個點跟源點的最短距離
(前面實作的vis陣列就是在維護這個東西)
CSES-Message Route
小明的網路有n台電腦和m條網路線分別連接兩台電腦
請問使用電腦1的阿強能不能傳送訊息給使用電腦n的小美呢?
如果可以, 它們經過的路徑上最少會有幾台電腦?
會經過哪些電腦?
link: https://cses.fi/problemset/task/1667
CSES-Message Route
從節點1做BFS
如果能走到節點n就有(最短)路徑
至於最短路徑上會經過哪些節點
只要在BFS完之後從終點往距離比它小1的點走
再往距離比它小1的點走
直到走到起點就會是最短路徑上的節點
深度優先搜尋
時間複雜度:O(V + E)
實作難度: 超好寫
找連通塊數量: Yes
找最短路徑: No
更多其他變體...
廣度優先搜尋
時間複雜度:O(V + E)
實作難度: 好寫
找連通塊數量: Yes
找最短路徑: Yes
比較
延伸的演算法
- Flood Fill(方格上的BFS)
- 0-1BFS(在權重只有0和另一個數字時的BFS)
Link: https://hackmd.io/tZitG_PfT622QxSAdc7YOA
Link: https://codeforces.com/blog/entry/22276
最短路徑問題
基本定義
在最短路徑問題裡 我們會有一張帶權有向圖
定義一個路徑p = <v0, v1, ..., vk>的權重w(p)為路徑上的邊權總和
並定義δ(u, v)為節點u到節點v的最短路徑權重
只要滿足w(p) = δ(u, v), p = <u, ..., v>的路徑p, 就稱為最短路徑
例子
w(<0, 1, 3>) = 4, w(<0, 2, 3>) = 5
δ(0, 3) = 4
所以路徑<0, 1, 3>是一條最短路徑
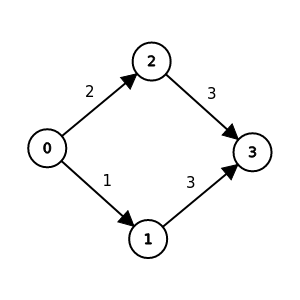
問題本體
在這裡我們只會討論單點源最短路徑問題
也就是給定一張圖G(V, E)和一個源點S
我們想要找到源點到每個點的最短路徑
問題本體
在這裡我們只會討論單點源最短路徑問題
也就是給定一張圖G(V, E)和一個源點S
我們想要找到源點到每個點的最短路徑
而以下這些問題也都可以被轉換成單點源最短路徑問題
1. 單一終點最短路徑問題
2. 單一點對最短路徑問題
3. 全點對最短路徑問題
單一終點最短路徑問題
給定一個終點
求所有點到終點的最短路徑
單一終點最短路徑問題
給定一個終點
求所有點到終點的最短路徑
只要把所有邊反向, 以終點為源點
就變成單點源最短路徑問題了
單一點對最短路徑問題
給定一個點對(u, v)
求u到v的最短路徑
單一點對最短路徑問題
給定一個點對(u, v)
求u到v的最短路徑
以u當源點做單點源最短路徑問題時
就已經解決單一點對最短路徑問題了
全點對最短路徑問題
對於所有的點對
求出它們之間的最短距離
全點對最短路徑問題
對於所有的點對
求出它們之間的最短距離
把每個點都當成源點各做一次單點源最短路徑問題就解決了
全點對最短路徑問題
對於所有的點對
求出它們之間的最短距離
把每個點都當成源點各做一次單點源最短路徑問題就解決了
值得一提的是全點對最短路徑問題其實有自己的演算法
ex. Floyd-Warshall/Johnson's
時間複雜度會比跑V次單點源還要快
不過礙於篇幅 這邊暫時不會提到
關於負權邊
在討論最短路徑時
最短路徑上是可以有負權邊的
但是不可以有負環(i.e.權重和為負的環)
不然就可以透過一直繞負環來得到更短的路徑
關於負權邊
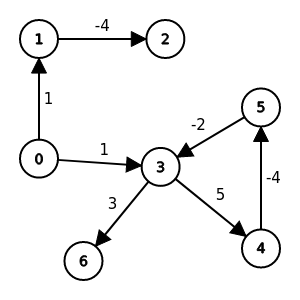
源點為0, 終點為2的最短路徑是<0, 1, 2>
源點為0, 終點為6的點對並沒有最短路徑
關於環
除了負環, 最短路徑上也不可以有正環
因為我們可以把正環從路徑上拔掉來得到更短的路徑
關於環
路徑<0, 1, 2, 3, 1, 4>不會是最短路徑
路徑<0, 1, 4>是最短路徑
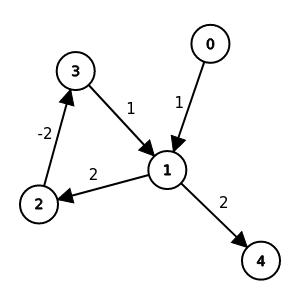
關於環
最短路徑上可以有零環
但把零環拔掉後也能產生最短路徑
關於環
路徑<0, 1, 2, 3, 1, 4>是最短路徑
路徑<0, 1, 4>也是最短路徑
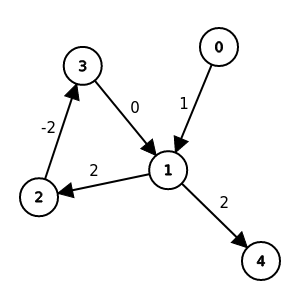
關於環
所以在處理最短路徑時
可以不考慮任何形式的環
因此一條最短路徑最多只會經過V個點, V - 1條邊
鬆弛(relaxtion)
接下來的演算法會先對每個點v設"估計最短路徑權重"v.d為INF
源點則設s.d = 0
並透過"鬆弛"來降低"估計最短路徑權重"
最後使得"估計最短路徑權重" = "最短路徑權重", 即
鬆弛(relaxtion)
而所謂的"鬆弛"就是當一條邊(u, v)滿足下列不等式時
就將v.d設為u.d + w(u, v)
白話來說就是
當我看到一條邊(u, v) 並且從u走這條邊到v時
會比目前我找到的v的"估計最短距離"還要短
那我就更新v的"估計最短距離"為
u的"估計最短距離" + 走過這條邊的權重
鬆弛(relaxtion)
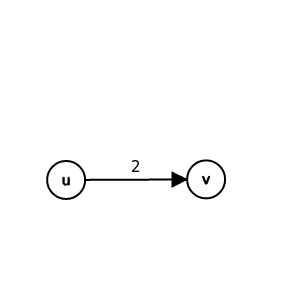
鬆弛前:
鬆弛條件:
鬆弛後:
鬆弛(relaxation)

鬆弛前:
鬆弛條件:
無法鬆弛
最短路徑及鬆弛的性質
三角不等式(triangle inequality):
對於圖上所有邊(u, v), 我們有
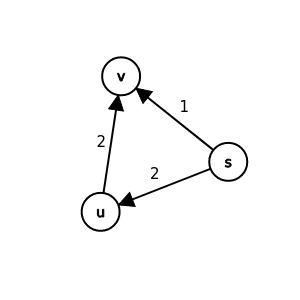
最短路徑及鬆弛的性質
三角不等式(triangle inequality):
對於圖上所有邊(u, v), 我們有
簡單的證明:
假設上述式子不成立, 即
那我們就可以從s走到u再走這條邊到v
使得s到v的最短路徑權重比δ(s, v)還小
那麼δ(s, v)就不是最短路徑權重
與δ的定義矛盾 因此假設錯誤
最短路徑及鬆弛的性質
上界性質(upper-bound property):
對於圖上的每個節點v, 我們有
最短路徑及鬆弛的性質
上界性質(upper-bound property):
證明:
設鬆弛次數為x
首先, 在一開始(x = 0)時此性質必滿足, 因為
最短路徑及鬆弛的性質
上界性質(upper-bound property):
證明:
假設在x次鬆弛之後保持這個性質,
證明第(x + 1)次鬆弛也會保持這個性質
假設鬆弛的邊是(u, v), 則我們有
(假設條件)
(三角不等式)
最短路徑及鬆弛的性質
上界性質(upper-bound property):
證明:
我們已經證明當x = 0時, 此性質滿足
當x是任意非負整數時滿足, 則x + 1時也滿足
因此 以數學歸納法得證
最短路徑及鬆弛的性質
收斂性質(convergence property):
假設任一條最短路徑(s, ..., u, v)
只要在relax(u, v)之前 u.d = δ(s, u)
那麼在relax(u, v)之後 v.d = δ(s, v)
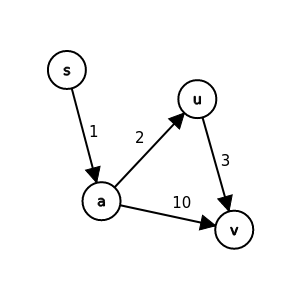
最短路徑及鬆弛的性質
收斂性質(convergence property):
假設任一條最短路徑(s, ..., u, v)
只要在relax(u, v)之前 u.d = δ(s, u)
那麼在relax(u, v)之後 v.d = δ(s, v)
這東西應該蠻直覺的
就先不證明了(´・ω・`)
最短路徑及鬆弛的性質
路徑鬆弛性質(path relaxation property):
考慮一條最短路徑p = <v0, v1, ..., vk>
只要在relax的順序中有
relax(v0, v1), relax(v1, v2), ..., relax(vk - 1, vk)
那麼就會滿足vk.d = δ(s, vk)
(即使中間穿插其他邊的relax也沒關係)
最短路徑及鬆弛的性質
證明:
用數學歸納法證明當第i條邊(vi - 1, vi)被relax時會滿足
首先, i = 0時滿足
(s = v0)
假設relax第i條邊後滿足vi.d = δ(s, vi)
那麼在relax(vi, vi+1)後
根據convergence property 必定會滿足
最短路徑及鬆弛的性質
證明:
證明完i = 0時滿足條件
假設relax第i條邊後滿足條件, 則relax第i + 1條邊也滿足條件
因此 以數學歸納法得證

Bellman-Ford
Algorithm
啟發
回想一下剛剛的path relaxation property
白話來說就是假設任意一條最短路徑s -> v
只要我們依照路徑上邊的順序relax
就可以算出v的最短路徑
那如果隨便亂relax呢?
每一輪都把所有的邊relax一遍
最差會需要relax幾輪才能算出所有點的最短路徑權重?
啟發
剛剛有提到每個點的最短路徑最長都只會經過V個點
所以當我們一口氣relax所有邊之後
每條最短路徑都至少多一個點算出最短路徑權重
因此只要relax V - 1輪所有邊就可以得到全部點的最短路徑權重
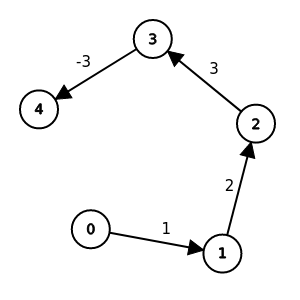
啟發
那如果圖上有源點可以走到的負環呢?
那麼就會有路徑可以藉由多繞幾圈負環得到更短的路徑
也就意味著在第V輪relax時會發現還有邊可以relax
核心想法
Bellman-Ford的核心想法就是這樣
對所有邊relax V - 1輪就可以得到所有點的最短路徑
如果在第V輪relax還有邊可以relax時
就代表圖上有源點可以走到的負環
過程
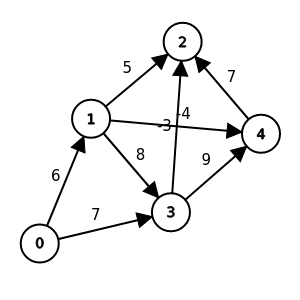
畫圖時間again!
實作
vector<pair<int, int> > G[2500];
int d[2500];
bool BellmanFord(int S) {
for(int i = 0; i < n; i++)
d[i] = INT_MAX / 2;
d[S] = 0;
for(int i = 0; i < n - 1; i++) {
for(int j = 0; j < n; j++) {
if (d[j] == INT_MAX / 2)
continue;
for(auto [to, w] : G[j])
if (d[j] + w < d[to])
d[to] = d[j] + w;
}
}
for(int i = 0; i < n; i++) {
if (d[i] == INT_MAX / 2)
continue;
for(auto [to, w] : G[i])
if (d[i] + w < d[to])
return false;
}
return true;
}實作
vector<pair<int, int> > G[2500];
int d[2500];
bool BellmanFord(int S) {
for(int i = 0; i < n; i++)
d[i] = INT_MAX / 2;
d[S] = 0;
for(int i = 0; i < n - 1; i++) {
for(int j = 0; j < n; j++) {
if (d[j] == INT_MAX / 2)
continue;
for(int k = 0; k < G[j].size(); k++)
if (d[j] + G[j][k].second < d[G[j][k].first])
d[G[j][k].first] = d[j] + G[j][k].second;
}
}
for(int i = 0; i < n; i++) {
if (d[i] == INT_MAX / 2)
continue;
for(int j = 0; j < G[i].size(); j++)
if (d[i] + G[i][j].second < d[G[i][j].second])
return false;
}
return true;
}複雜度
我們會對每條邊relax V次
一共有E條邊
所以Bellman-Ford的時間複雜度是O(VE)
UVA558-wormholes
在宇宙中有n個星系m個蟲洞
人類可以透過連接兩個星系的蟲洞來穿梭星系之間
且你所在的太陽系一定可以走到任何其他星系
這些蟲洞都是單向, 連接不同星系
有些蟲洞可能會讓你跑到未來的x年後
有些可能會讓你跑到過去的x年前
而有個聰明科學家想知道能不能穿梭形成環的一些蟲洞
讓他可以一直回到過去 親眼見證宇宙大霹靂呢?
UVA558-wormholes
就是圖上判負環的裸題
Bellman-Ford砸下去就好了
link: https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=680&page=show_problem&problem=499
Dijkstra's
Algorithm
啟發
這個演算法是Dijkstra在咖啡館喝咖啡的時候想到的
所以多喝咖啡應該就會懂Dijkstra's演算法了
啟發
從鹿特丹到格羅寧根的最短路徑是什麽?
實際上,這就是對於任意兩座城市之間的最短路問題。
解決這個問題大概只花了我20分鐘:
一天早上,我和我的未婚妻在阿姆斯特丹購物,
累了,我們便坐在咖啡館的露台上喝咖啡,
然後我就試了一下能否用一個算法解決最短路問題。

核心想法
Dijkstra's演算法的核心想法是
對一個沒有負權邊的圖維護一個空的點集S
和一個有所有點的點集Q
然後執行以下步驟直到點集Q是空的
1. 從Q中拿出一個"估計最短路徑權重"最小的點v
2. relax所有從v開始的邊
3. 把v從Q刪除, 並加到S裡面
Dijkstra's演算法可以保證在S裡面的所有點都已經找到最短路徑
所以當Q中的點都跑到S時
所有點就都找到最短路徑了
證明
現在要證明的是
只要一個點v進入點集S時 必定已找到最短路徑, 即
(然後根據upper bound property, v到結束前都會滿足這個條件)
證明
首先
我們假設某個點u是第一個進入點集S但沒有找到最短路徑的點
這個點不可能是源點, 因為
也不可能是源點走不到的點, 因為
只要一個點v進入點集S時 必定已找到最短路徑, 即
證明
所以這個點的最短路徑一定是<s, ..., u>
既然s不會是第一個不滿足條件的點, 又是第一個被丟進S的點
那當u要丟進S時, s一定在S裡, u一定在Q裡
所以我們可以把到v的最短路徑分解成
只要一個點v進入點集S時 必定已找到最短路徑, 即
其中y是路徑上第一個不在S的點
x則是y的前一個點
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
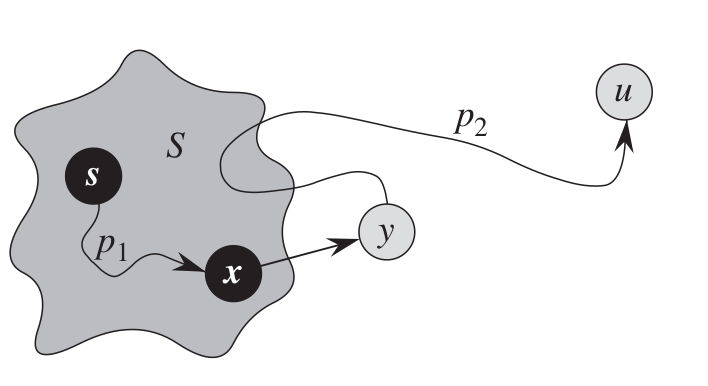
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
由於x在S裡, u又是第一個不符合條件的點
x一定滿足條件
而當x丟進S時會relax(x, y)
根據convergence property, y也會滿足條件
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
由於x在S裡, u又是第一個不符合條件的點
x一定滿足條件
而當x丟進S時會relax(x, y)
根據convergence property, y也會滿足條件
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
然後因為所有邊的邊權都是非負的
那y到u的最短路徑至少會是0
所以我們有
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
接下來根據upper bound property
我們有
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
最後
因為現在要丟進S的點是u, 而y還不在u裡面
加上我們是選Q中"估計最短路徑權重"最小的點
所以我們有
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
把我們有的所有式子串在一起
就會有
把式子簡化一下會變成
證明
只要一個點v進入點集S時 必定已找到最短路徑, 即
推導到最後可以發現u丟進S時就已經找到最短路徑
跟假設產生矛盾
因此不存在任何點丟進S時會還沒找到最短路徑
從想法到實作
空的點集S, 有所有點的點集Q
執行以下步驟直到點集Q是空的
1. 從Q中拿出一個"估計最短路徑權重"最小的點v
2. relax所有從v開始的邊
3. 把v從Q刪除, 並加到S裡面
證明完Dijkstra's演算法的正確性後
來回想一下演算法本身
從想法到實作
空的點集S, 有所有點的點集Q
執行以下步驟直到點集Q是空的
1. 從Q中拿出一個"估計最短路徑權重"最小的點v
2. relax所有從v開始的邊
3. 把v從Q刪除, 並加到S裡面
要如何從一個點集中有效率的找出
"估計最短路徑權重"最小的點?
從想法到實作
空的點集S, 有所有點的點集Q
執行以下步驟直到點集Q是空的
1. 從Q中拿出一個"估計最短路徑權重"最小的點v
2. relax所有從v開始的邊
3. 把v從Q刪除, 並加到S裡面
將問題再抽象化一下
不就是要從一堆元素中找最小值嗎?
從想法到實作
空的點集S, 有所有點的點集Q
執行以下步驟直到點集Q是空的
1. 從Q中拿出一個"估計最短路徑權重"最小的點v
2. relax所有從v開始的邊
3. 把v從Q刪除, 並加到S裡面
有沒有什麼資料結構能夠很快的找一堆元素中的最小值呢?
從想法到實作
空的點集S, 有所有點的點集Q
執行以下步驟直到點集Q是空的
1. 從Q中拿出一個"估計最短路徑權重"最小的點v
2. relax所有從v開始的邊
3. 把v從Q刪除, 並加到S裡面
有沒有什麼資料結構能夠很快的找一堆元素中的最小值呢?
priority queue!
實作
由於STL的priority_queue沒辦法在點被relax時
直接更動pq裡面對應點的值
所以我們把一個點v和它丟進去當下的"估計最短路徑權重"綁起來丟進去
如果從pq拿出來時 它身上帶的值和目前的"估計最短路徑權重"不一樣的話
就判定這個資料是過時的 直接無視並丟掉
實作
const int N = 100000;
vector<pair<int, int> > G[N];
int d[N];
priority_queue<pair<int, int>, vector<pair<int, int> >,
greater<pair<int, int> > > pq;
void Dijkstra(int s) {
for(int i = 0; i < N; i++)
d[i] = INT_MAX / 2;
d[s] = 0;
for(int i = 0; i < N; i++)
pq.push(make_pair(d[i], i));
while(!pq.empty()) {
auto [dis, now] = pq.top();
pq.pop();
if (dis != d[now])
continue;
for(auto [to, w] : G[now]) {
if (dis + w < d[to]) {
d[to] = dis + w;
pq.push(make_pair(d[to], to));
}
}
}
}實作
const int N = 100000;
vector<pair<int, int> > G[N];
int d[N];
priority_queue<pair<int, int>, vector<pair<int, int> >,
greater<pair<int, int> > > pq;
void Dijkstra(int s) {
for(int i = 0; i < N; i++)
d[i] = INT_MAX / 2;
d[s] = 0;
for(int i = 0; i < N; i++)
pq.push(make_pair(d[i], i));
while(!pq.empty()) {
int dis = pq.top().first, now = pq.top().second;
pq.pop();
if (dis != d[now])
continue;
for(int i = 0; i < G[now].size(); i++) {
int to = G[now][i].first, w = G[now][i].second;
if (dis + w < d[to]) {
d[to] = dis + w;
pq.push(make_pair(d[to], to));
}
}
}
}複雜度
最差情況下每條邊都會鬆弛一次
所以最多對pq插入移除O(E)次
而pq最多會有O(E)個元素
所以時間複雜度是O(ElgE)
CSES Shortest Route I改
發財國有n個城市和m條單向道路
每條道路各自不同的長度是c
請問從城市1到每個城市的最短距離各是多少?
CSES Shortest Route I改
Dijkstra's裸題?
CSES Shortest Route I改
Dijkstra's裸題?
Wrong Answer!
CSES Shortest Route I改
Dijkstra's裸題?
Wrong Answer!
切記Dijkstra's的正確性是建立在圖沒有負權邊的前提下
CSES Shortest Route I改
題目的限制砸O(VE)的Bellman-Ford即可
CSES Shortest Route I
發財國有n個城市和m條單向道路
每條道路各自不同的長度是c
請問從城市1到每個城市的最短距離各是多少?
Link: https://cses.fi/problemset/task/1671
CSES Shortest Route I
這次就是Dijkstra's裸題了
110北二區學科能力競賽 pD

110學科能力競賽-資訊科 pD
看起來像是單點源最短路徑問題
但是多了"轉乘"的概念
110學科能力競賽-資訊科 pD
看起來像是單點源最短路徑問題
但是多了"轉乘"的概念
要怎麼處理"最多轉乘1次"這個限制?
110學科能力競賽-資訊科 pD
首先先把情況分兩種
1. 我到節點v時還沒轉乘過
2. 我到節點v時已經轉乘過了
110學科能力競賽-資訊科 pD
首先先把情況分兩種
1. 我到節點v時還沒轉乘過
2. 我到節點v時已經轉乘過了
對於第1種狀況我們可以選擇要轉乘或不轉乘
對於第2種狀況我們只能走原本所在的路線上
110學科能力競賽-資訊科 pD
如果把圖也依照狀況分成兩層呢?
110學科能力競賽-資訊科 pD
如果把圖也依照狀況分成兩層呢?
分成沒轉乘過的部份
和轉乘過的部份
沒轉乘過的部份在可以轉乘的點上
都往轉乘過的圖上同個點蓋一條邊權0的邊
走過這條邊就意謂轉乘過了
且不能再轉乘了
110學科能力競賽-資訊科 pD
拿範例來畫個圖應該會比較了解
再次召喚白板!

110學科能力競賽-資訊科 pD
最後再對每個節點分別維護
"目前走1號線的估計最短路徑權重"和
"目前走2號線的估計最短路徑權重"
就可以開心的砸Dijkstra's了
AC!
延伸的演算法
- Dijkstra's Algorithm(稠密圖上O(V^2)的實作)
- Floyd-Warshall(O(V^3)全點對最短路徑演算法)
- Johnson's Algorithm(O(VElgV)全點對最短路徑演算法)
- topological sort(O(V + E)有向無環圖上最短路徑演算法)
Link: https://cp-algorithms.com/graph/dijkstra.html
Link: https://csacademy.com/lesson/topological_sorting/
樹
基本定義
所謂的樹指的是一張連通無環的圖
擁有V個節點和V - 1個邊
由於樹擁有很多圖沒有的性質
在樹上有更多的演算法可以發掘
基本定義
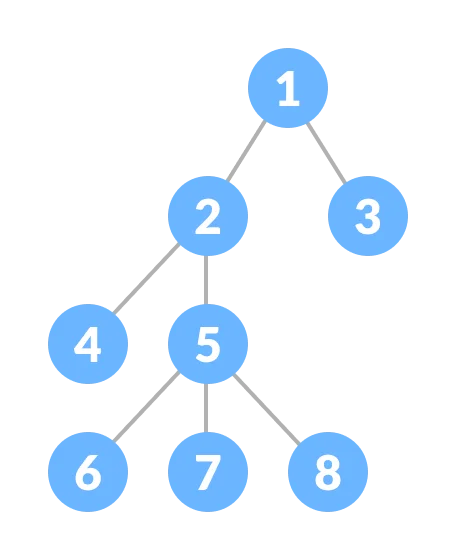
根(root)/深度(depth)

根是樹上任意選定的一個點
以它當成深度0的基準
而每個點的深度就是和根的距離
根(root)/深度(depth)

ex.
以節點1為根的話
節點1深度 = 0
節點2, 3深度 = 1
節點4, 5深度 = 2
節點6, 7, 8深度 = 3
父節點(parent)/子節點(child)

對於兩個相鄰的節點
深度較大的節點是深度較小節點的子節點
深度較小的節點是深度較大節點的父節點
父節點(parent)/子節點(child)

ex.
以節點1為根的話
節點6, 7, 8是節點5的子節點
節點2是節點5的父節點
兄弟(sibling)

擁有相同父節點的節點互為兄弟
兄弟(sibling)

ex.
以節點1為根的話
節點6, 7, 8為兄弟
因為它們有共同的父節點5
祖先(ancestor)/子孫(descendant)

如果一個節點在節點v到根的簡單路徑上
那個節點就是節點v的祖先
反之, v是那些節點的子孫
祖先(ancestor)/子孫(descendant)

ex.
以節點1為根的話
節點5的祖先有節點1, 2, 5
節點2的子孫有節點2, 4, 5, 6, 7, 8
子樹(subtree)

一個節點的子樹是只包含它所有子孫的樹
子樹(subtree)

ex.
以節點1為根的話
節點5的子樹有節點5, 6, 7, 8
葉子(leaf)

葉子是指沒有任何子節點的節點
葉子(leaf)

ex.
以節點1為根的話
節點3, 4, 6, 7, 8是葉子
樹的一些性質

1. 樹上任兩點只會有一條簡單路徑
2. 在樹上隨便加一條邊就會產生環
3. 在樹上隨便拔一條邊樹就會變得不連通
CSES Subordinates
一家公司有n個員工
給你公司所有的上司下屬關係
請問每個員工各自有多少個下屬(除了自己的子孫)
保證關係圖會形成一棵樹
Link: https://cses.fi/problemset/task/1674
CSES Subordinates
就是數每個節點的子樹大小-1是多少的問題
我們可以在DFS的時候開一個變數儲存當前的子樹大小
並讓DFS回傳該節點的子樹大小
而一個子樹的大小就是1+所有子節點的子樹大小
所以只要把1加上所有往下DFS時回傳的值
就會是當前節點的子樹大小
最小生成樹
Minumum Spanning Tree
前沿
假設你開了一家電力公司要提供一些住家或是商家電力
且已知在任意兩個服務對象之間牽電纜所需的資金
由於牽電纜會需要龐大的資金
所以你想要找到最便宜的方式牽電纜
使得發電廠可以將電送到每個服務的對象
(發電廠和所有服務對象連通)
前沿
如果把服務對象看成節點
每條可以牽的電纜看成連接節點之間的邊
牽電纜所需的資金看成邊權的話
我們其實就是在找到一種挑邊的方法
使得每個節點都互相連通
同時最小化挑到的邊的邊權總和
(結果一定是一棵樹)
(不然拔掉一些邊還是可以連通, 且權重和更小)
最小生成樹問題
把問題抽象化再重新定義一次
最小生成樹問題想要解決的是
給定一張圖
我們想從中挑出V-1條邊
讓所有節點形成一棵樹
並最小化這些邊的邊權總和
最小生成樹問題
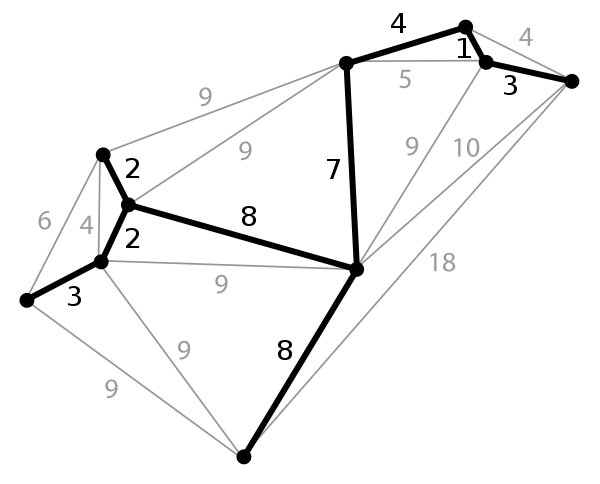
最小生成樹相關定理
在說明定理之前先定義一些事情
給定一張帶權無向圖G(V, E)
如果將節點分成兩個集合S和V-S
那這就叫這張圖的一個割(cut)
最小生成樹相關定理
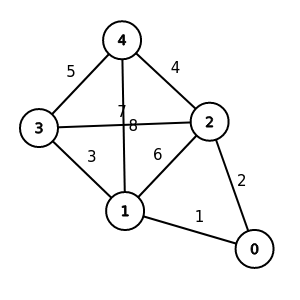
一個cut(S, V-S)
S = {0, 1}, V-S = {2, 3, 4}
最小生成樹相關定理

一個cut(S, V-S)
S = {0, 1, 4}, V-S = {2, 3}
最小生成樹相關定理
假設我們已經挑好一些邊是某個生成樹邊集的子集
這些邊形成的邊集叫A
(這些邊會形成一些較小的生成樹)
那我們稱一個cut(S, V-S) respect to A
如果我們挑的邊集A當中
沒有邊連接S中的點和V-S中的點
(我真的不知道respect怎麼翻成中文qq)
最小生成樹相關定理
假設我們有一個cut(S, V-S)
那我們說一條邊跨過這個cut
如果它連接S中的某個點到V-S中的某個點
而在所有跨過cut的邊當中
權重最小的那條邊被稱作"輕邊"
最小生成樹相關定理
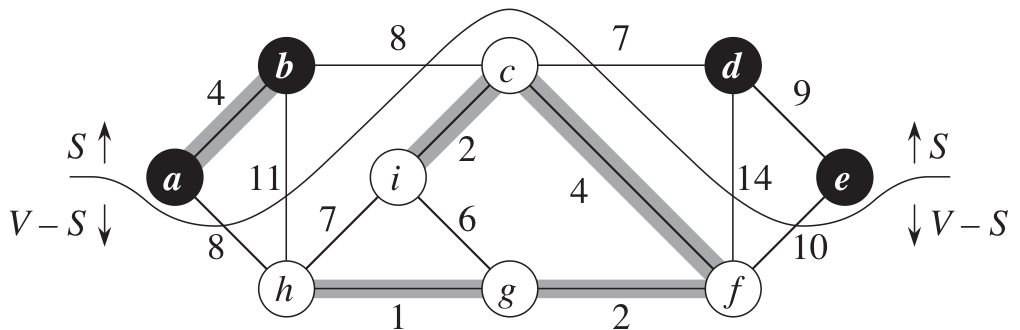
這個cut respect to A
因為A裡面的邊都沒有跨過這個cut
(輕邊邊權為7)
最小生成樹相關定理
這個cut也respect to A
因為A裡面的邊都沒有跨過這個cut
(輕邊邊權為7)
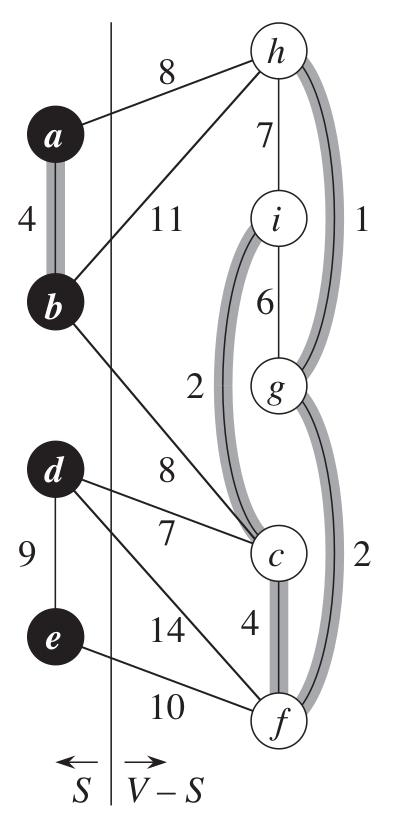
最小生成樹相關定理
定理:
給定一個無向連通圖G(V, E)
和屬於這張圖的最小生成樹的邊集的子集A
並隨便找一個cut respect to A
那麼把跨過這個cut中的輕邊(u, v)
加入邊集A產生邊集A'
A'還是某個最小生成樹的邊集的子集
最小生成樹相關定理
證明:
假設有個最小生成樹T不包含這個輕邊(u, v)
那麼由於(u, v)跨過cut
T上節點u到v的簡單路徑上
至少有一條邊也跨過cut
我們稱這條邊為(x, y)
最小生成樹相關定理
證明:
將這條邊從T移除會使其分成2個連通塊
再將(u, v)加上去就會讓它重新連通
產生新的生成樹T'
最小生成樹相關定理
證明:
由於加上去的邊(u, v)是輕邊
所以我們有
最小生成樹相關定理
證明:
而T根據假設是一個最小生成樹
所以把(x, y)拔掉並加上(u, v)不會使生成樹更小, 即
最小生成樹相關定理
證明:
最後合併兩式
可以得到
所以拔掉(x, y)加上(u, v)會得到權重跟T一樣的生成樹
即最小生成樹
最小生成樹相關定理
證明:
所以即使有最小生成樹T不包含我們挑的輕邊
我們還是可以把T的某條邊拔掉換成這條輕邊
所以把這條輕邊加進A產生的A'還是最小生成樹的邊集的子集
Kruskal's Algorithm
核心想法
Kruskal's的想法很簡單
就是在所有邊中
從權重小到大的順序去看邊
如果當前這條邊的兩端目前不在同一個連通塊
就將這條邊加進邊集
反之無視這條邊
(否則會產生環, 違反最小生成樹的定義)
證明
為什麼一直選最小可以加進生成樹的邊就能產生最小生成樹呢?
證明
為什麼一直選最小可以加進生成樹的邊就能產生最小生成樹呢?
不會因為選到某些邊連接連通塊使得某些更好的邊不能選嗎?
證明
為什麼一直選最小可以加進生成樹的邊就能產生最小生成樹呢?
不會因為選到某些邊連接連通塊使得某些更好的邊不能選嗎?
透過剛剛的定理, 可以很清楚的告訴你
不會!
證明
回顧一下剛剛的定理:
給定一個無向連通圖G(V, E)
和屬於這張圖的最小生成樹的邊集的子集A
並隨便找一個cut respect to A
那麼把跨過這個cut中的輕邊(u, v)
加入邊集A產生邊集A'
A'還是某個最小生成樹的邊集的子集
證明
當我們選一條邊(u, v)加進生成樹A前
節點u, v會在不同的連通塊
那我們可以做一個cut(S, V-S)
使得S包含所有跟節點u同個連通塊的節點
那麼根據cut的方式, cut respect to A且v一定在V-S
那麼(u, v)就跨過這個cut
加上(u, v)是不在生成樹內最小權重的邊
所以(u, v)是個輕邊
證明
所以只要原本邊集是最小生成樹邊集的子集
加進新的邊也會是最小生成樹邊集的子集
聽起來很數歸...
證明
證明:
設邊集A是目前維護的生成樹邊集
當我們加入i = 0條邊時, A是空集合
所以A是某個最小生成樹的邊集的子集
假設加入i條邊後A是某個最小生成樹邊集的子集
那麼加入第i+1條邊之後A還是某個最小生成樹邊集的子集
(根據剛剛的推論)
證明
證明:
因此, 由數學歸納法得證
加完V - 1條邊之後A還是最小生成樹邊集的子集
由於最小生成樹邊集會有V - 1條邊
A是最小生成樹的邊集
從想法到實作
所以證明告訴我們Kruskal's的想法一定會產生最小生成樹
那我們來回想一下Kruskal是怎麼說的
從想法到實作
在所有邊中
從權重小到大的順序去看邊
如果當前這條邊的兩端目前不在同一個連通塊
就將這條邊加進邊集
反之無視這條邊
怎麼做?
從想法到實作
在所有邊中
從權重小到大的順序去看邊
如果當前這條邊的兩端目前不在同一個連通塊
就將這條邊加進邊集
反之無視這條邊
先把邊依照邊權排序就好了
從想法到實作
在所有邊中
從權重小到大的順序去看邊
如果當前這條邊的兩端目前不在同一個連通塊
就將這條邊加進邊集
反之無視這條邊
怎麼判斷兩個節點是不是在同個連通塊?
從想法到實作
在所有邊中
從權重小到大的順序去看邊
如果當前這條邊的兩端目前不在同一個連通塊
就將這條邊加進邊集
反之無視這條邊
DFS? 太慢了!
從想法到實作
在所有邊中
從權重小到大的順序去看邊
如果當前這條邊的兩端目前不在同一個連通塊
就將這條邊加進邊集
反之無視這條邊
我們需要一個能快速確認兩點是否連通的資料結構...
從想法到實作
在所有邊中
從權重小到大的順序去看邊
如果當前這條邊的兩端目前不在同一個連通塊
就將這條邊加進邊集
反之無視這條邊
我們需要一個能快速確認兩點是否連通的資料結構...
並查集!!!
實作
const int N = 100000;
int Kruskal(vector<pair<int, pii> > edge) {
sort(edge.begin(), edge.end());
int cost = 0;
disjointSet DSU(N);
for(auto [w, e] : edge) {
if (DSU.query(e.first) != DSU.query(e.second)) {
cost += w;
DSU.merge(e.first, e.second);
}
}
return cost;
}實作
const int N = 100000;
int Kruskal(vector<pair<int, pii> > edge) {
sort(edge.begin(), edge.end());
int cost = 0;
disjointSet DSU(N);
for(int i = 0; i < edge.size(); i++) {
int w = edge.first;
int u = edge.second.first, v = edge.second.second;
if (DSU.query(u) != DSU.query(v)) {
cost += w;
DSU.merge(u, v);
}
}
return cost;
}複雜度
會做O(E)次查詢
O(V)次合併
還有一次O(ElgE)的排序
如果並查集有做路徑壓縮+啟發式合併的話
查詢/合併一次是O(α(V))
加起來是ElgE + (V+E)(α(V))
所以時間複雜度是O(ElgE)
CSES Road Reparation
某個國家有n個城市和m條雙向道路
可是這些路實在太爛了
都沒辦法讓車子通行
告訴你每條路修好所需的價錢
你需要修好一些路使得每個城市之間都有路徑能抵達對方
請問最少需要多少錢呢?還是不可能辦到呢?
Link: https://cses.fi/problemset/task/1675/
CSES Road Reparation
最小生成樹裸題, 一樣Kruskal's砸下去就過了
唯一需要想的部份是要怎麼判定能不能產生最小生成樹?
CSES Road Reparation
最小生成樹裸題, 一樣Kruskal's砸下去就過了
唯一需要想的部份是要怎麼判定能不能產生最小生成樹?
只要它給你的邊能讓原圖連通就一定有最小生成樹
反之沒有
所以只要在做完Kruskal's時
用並查集檢查是不是每個點都在同個連通塊就好了
延伸的演算法
- Prim's Algorithm(稠密圖上O(V^2)最小生成樹演算法)
一些有趣的問題
不知道有沒有時間講(´・ω・`)
AtCoder Regular Contest 076 problem D
Link: https://atcoder.jp/contests/arc076/tasks/arc076_b
CSES Flight Discount
Link: https://cses.fi/problemset/task/1195
Codeforce 1513D
GCD and MST
Link: https://codeforces.com/problemset/problem/1513/D
參考資料
1. Introduction to algorithms, third edition
(俗稱CLRS, 很好的演算法教科書)
2. USACO guide
(https://usaco.guide/)
3. Competitive Programmer's Handbook
(https://usaco.guide/CPH.pdf)
4. 維基百科
(https://en.wikipedia.org/wiki/Main_Page)
題目來源
1. CSES problem set
(https://cses.fi/)
2. Codeforces
(https://codeforces.com/)
3. AtCoder
(https://atcoder.jp/)
4. Online Judge
(https://onlinejudge.org/index.php)
Basic Graph Theory
By shioko
Basic Graph Theory
- 89


