1.8 Representation Power of functions
Why do we need complex functions ?
Recap: Six jars
What we saw in the previous chapter?
(c) One Fourth Labs
None of them handle non-linear separable data
Why do we care about continuous functions ?
(c) One Fourth Labs
Recap: Continuous Functions
\(w_{t+1} = w_{t} - \eta \Delta w_{t} \)
\(b_{t+1} = b_{t} - \eta \Delta b_{t} \)
\( \Delta w_{t} = \frac{\partial L}{\partial w} \)
\( \Delta b_{t} = \frac{\partial L}{\partial b} \)
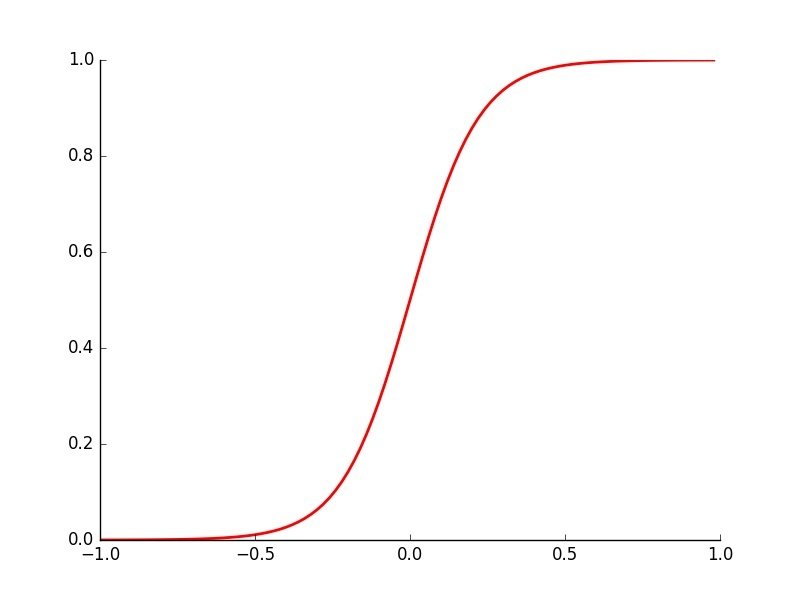
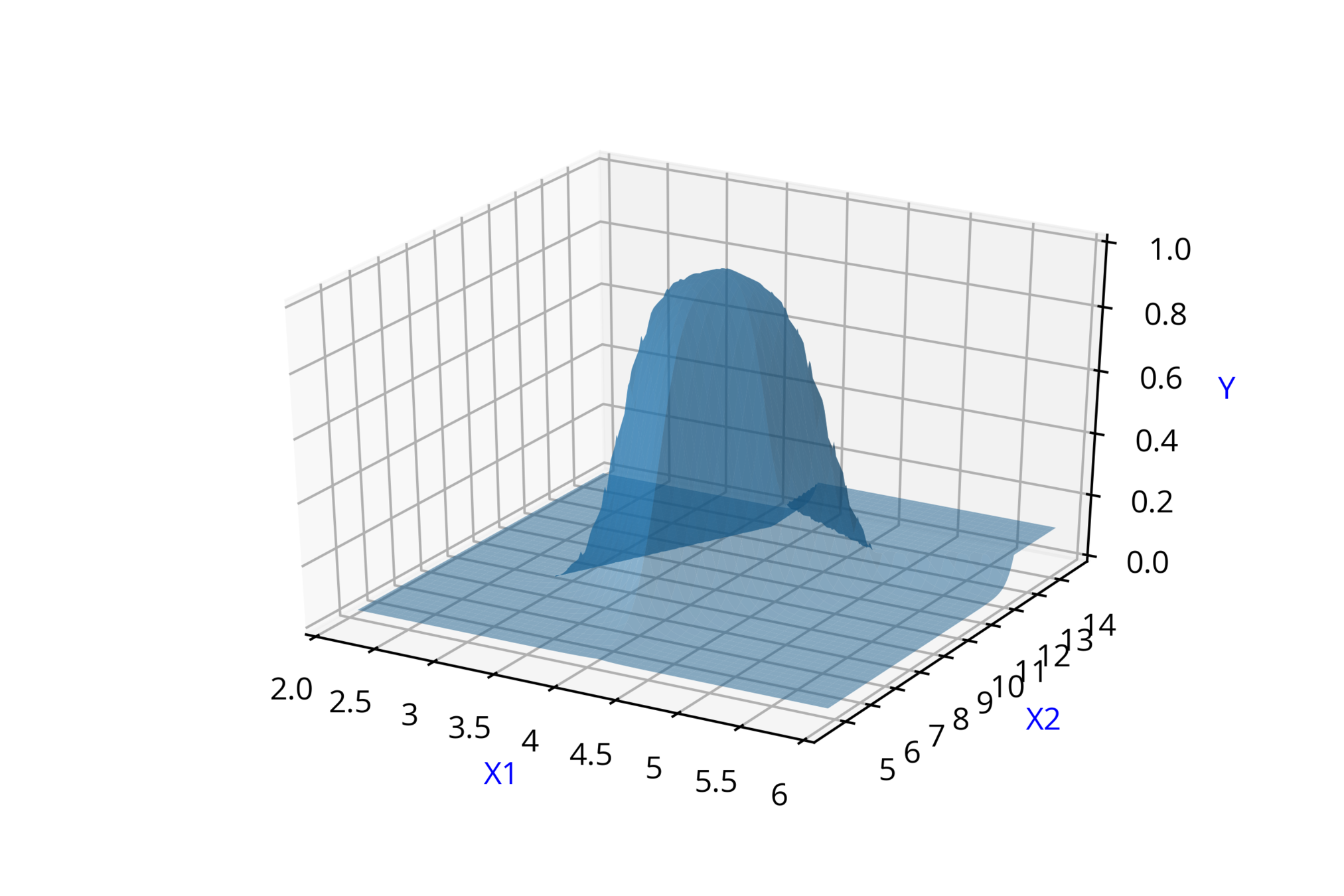
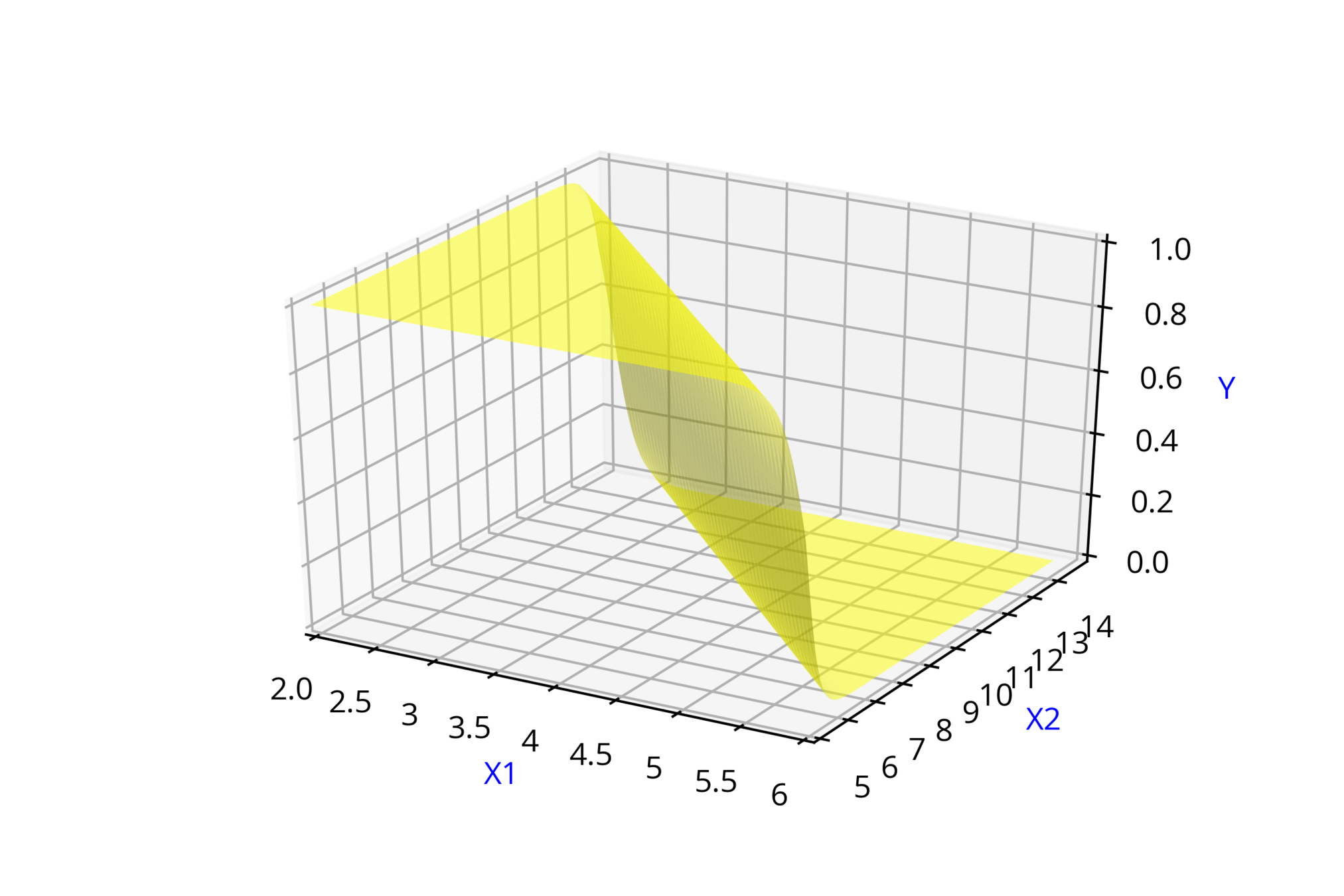
\( \hat{y} = \frac{1}{1+e^{-(2* x_1 +5)}} \)
\( \hat{y} = \frac{1}{1+e^{-(-2* x_1 + 2*x_2+20)}} \)
\( \hat{y} = sig_1(sig_2(x_1,x_2),sig_3(x_1,x_2),sig_4(x_1,x_2)) \)
*sig == sigmoid
Modeling Complex Relations
Why do we need complex functions ?
(c) One Fourth Labs
\( x_1 \)
\(x_2\)
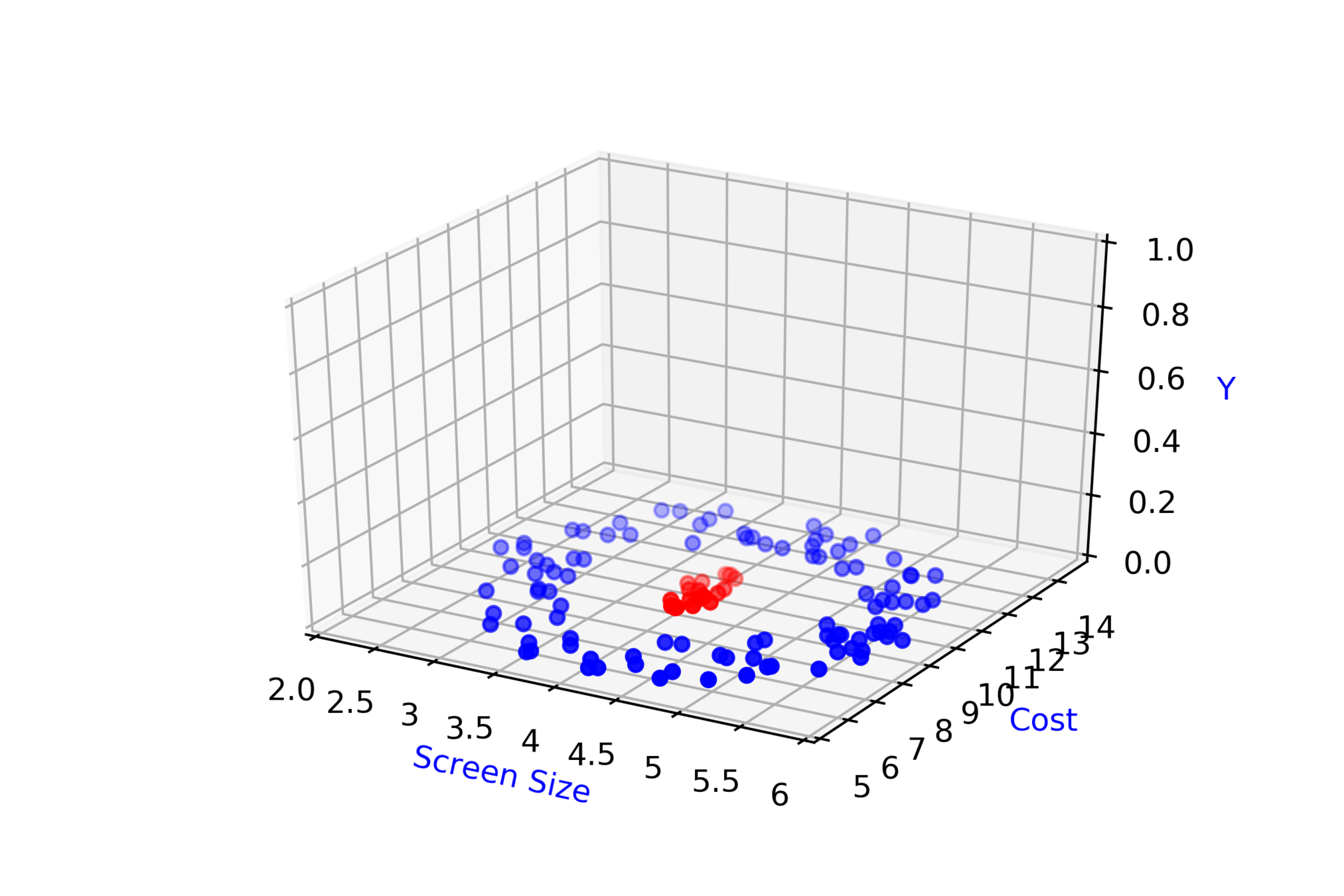
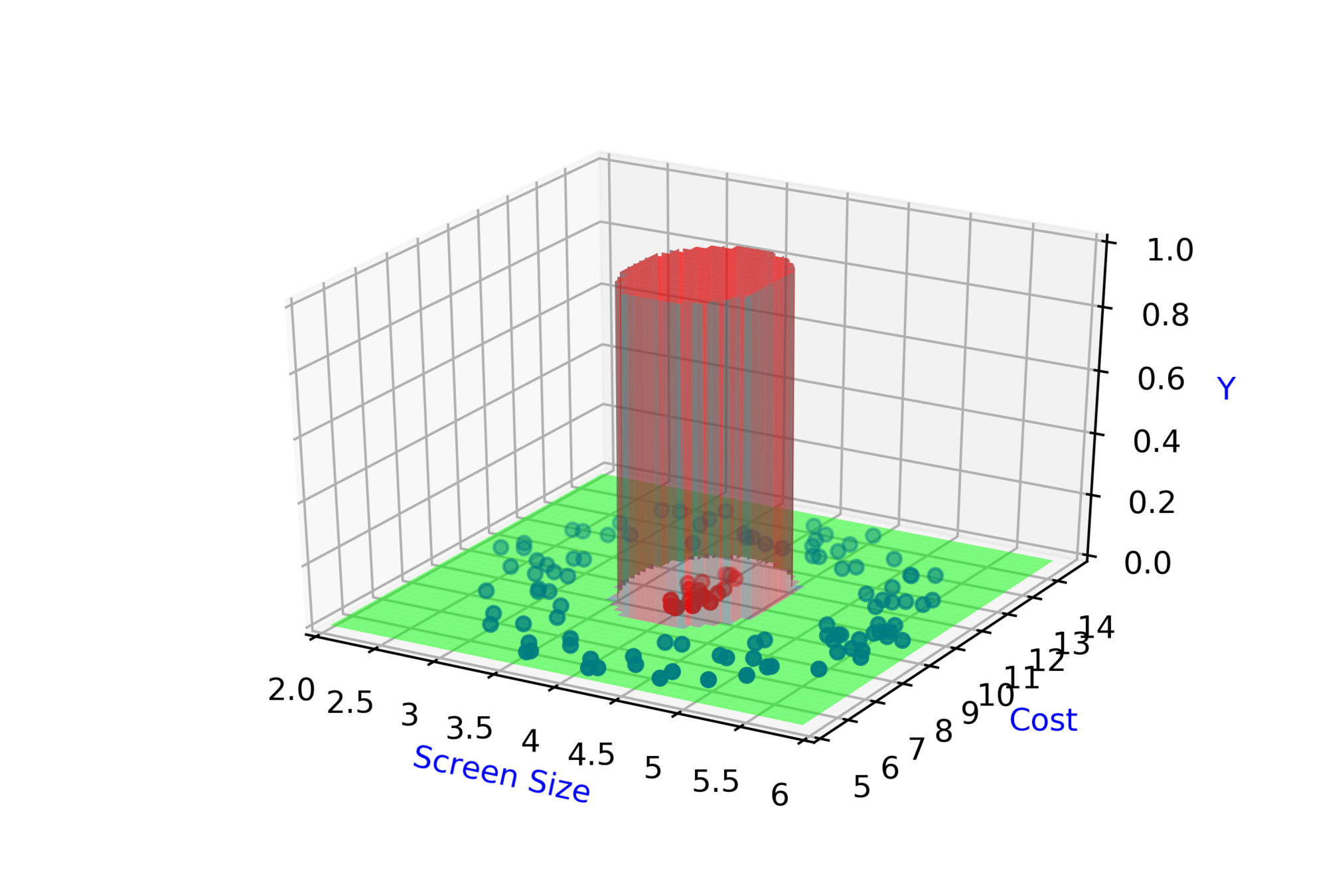
Screen Size
Cost
3.5
4.5
8k
12k
\( \hat{y} = \hat{f}(x_1,x_2) \)
\( \hat{y} = 1\)
\( \hat{y} = 0 \)
\( \hat{y} =\hat{f}(\hat{y_1},\hat{y_2},\hat{y_3},\hat{y_4}, w_9, w_{10}, w_{11},w_{12}, b_{5} )\)
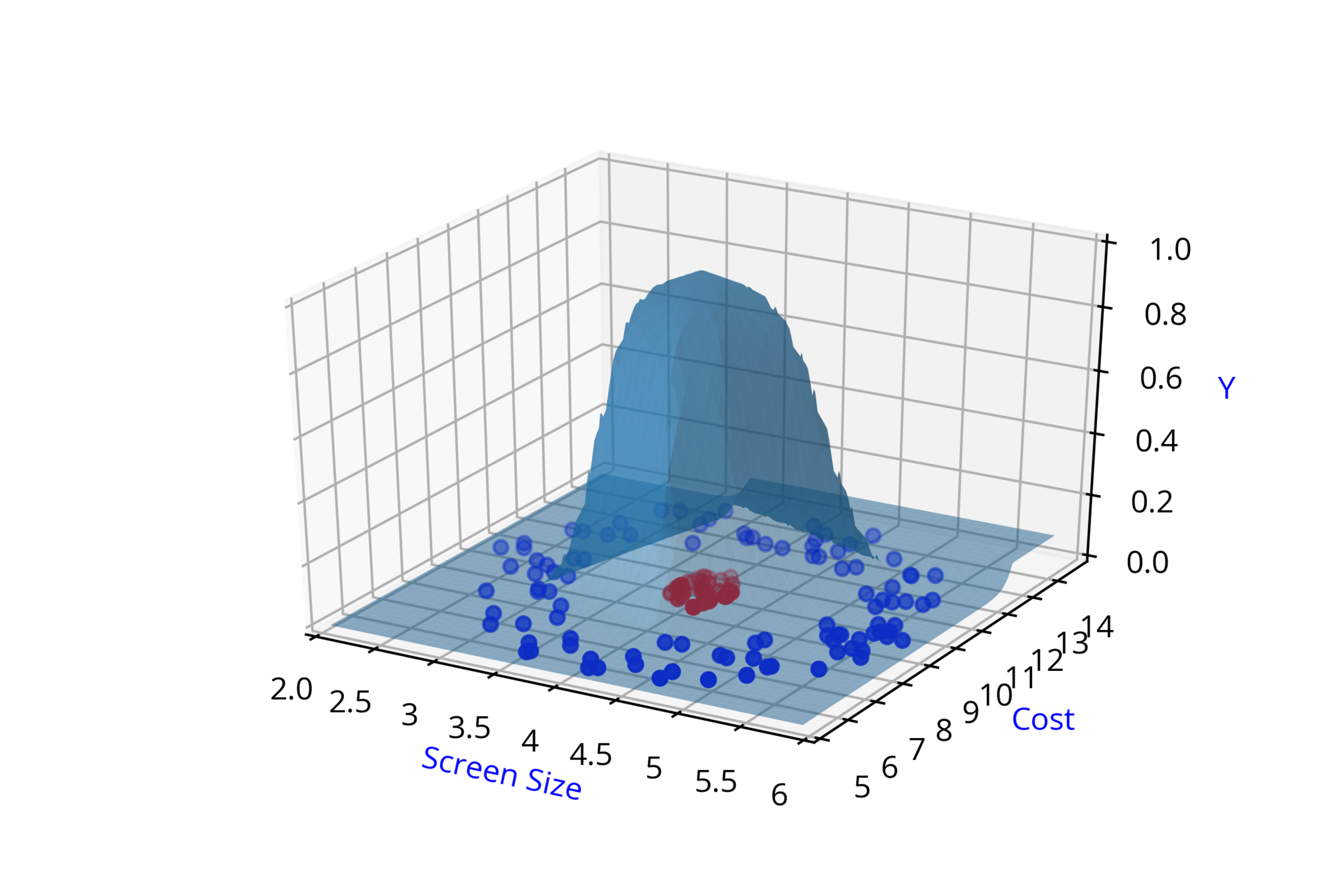
\( \hat{y_2} = \hat{f}(x_1,x_2,w_3,w_4,b_2) \)
\( \hat{y_1} = \hat{f}(x_1,x_2,w_1,w_2,b_1) \)
\( \hat{y_3} = \hat{f}(x_1,x_2,w_5,w_6,b_3) \)
\( \hat{y_4} = \hat{f}(x_1,x_2,w_7,w_8,b_4) \)
Modeling Complex Relations
Why do we need complex functions ?
(c) One Fourth Labs
\( \hat{y} = \hat{f}(x_1,x_2) \)
\( \hat{y} =\hat{f}(\hat{y_1},\hat{y_2},\hat{y_3},\hat{y_4}, w_9, w_{10}, w_{11},w_{12}, b_{5} )\)
\( \hat{y_2} = \hat{f}(x_1,x_2,w_3,w_4,b_2) \)
\( \hat{y_1} = \hat{f}(x_1,x_2,w_1,w_2,b_1) \)
\( \hat{y_3} = \hat{f}(x_1,x_2,w_5,w_6,b_3) \)
\( \hat{y_4} = \hat{f}(x_1,x_2,w_7,w_8,b_4) \)
\( \hat{y} = \frac{1}{1+e^{-(w_1* x_1 + w_2*x_2+b)}} \)
\(w_1\)
\(w_2\)
\(x_2\)
\(x_1\)
\( \hat{y} \)
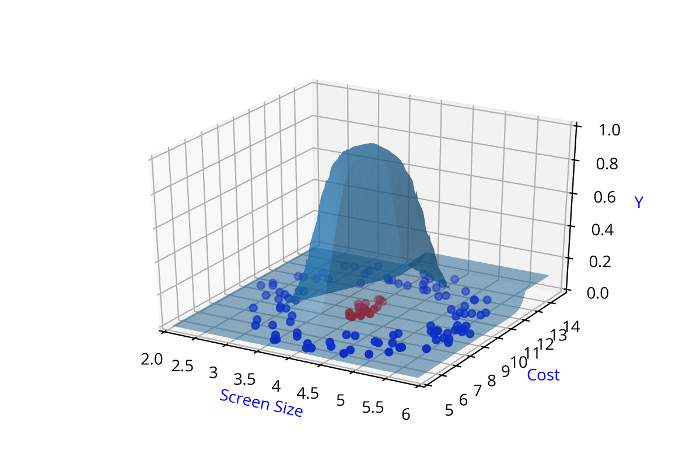
Are such complex functions seen in most real world examples ?
If so, how do I even come up with such complex functions?
Modeling Complex Relations
Are such complex functions seen in most real world examples ?
(c) One Fourth Labs
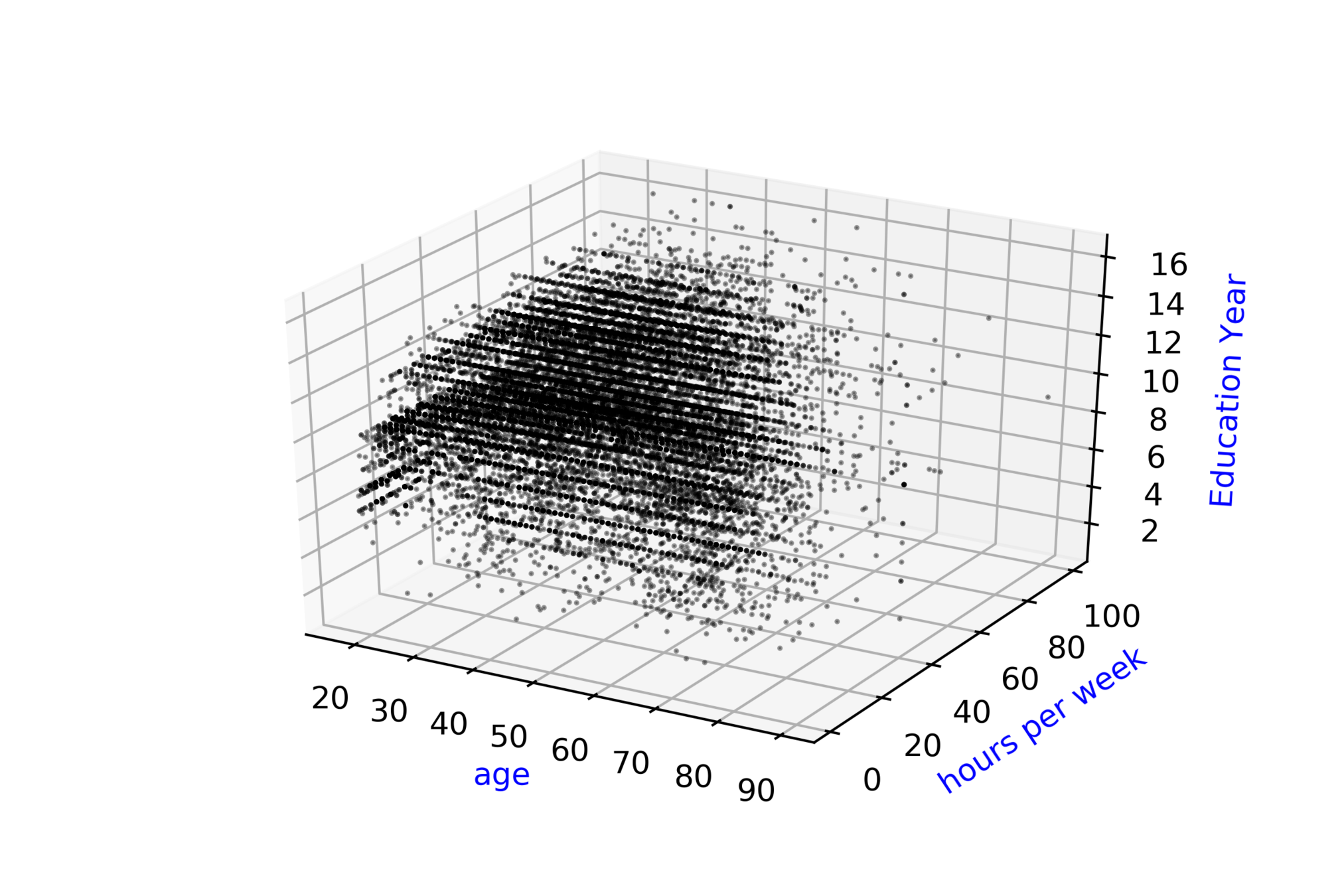
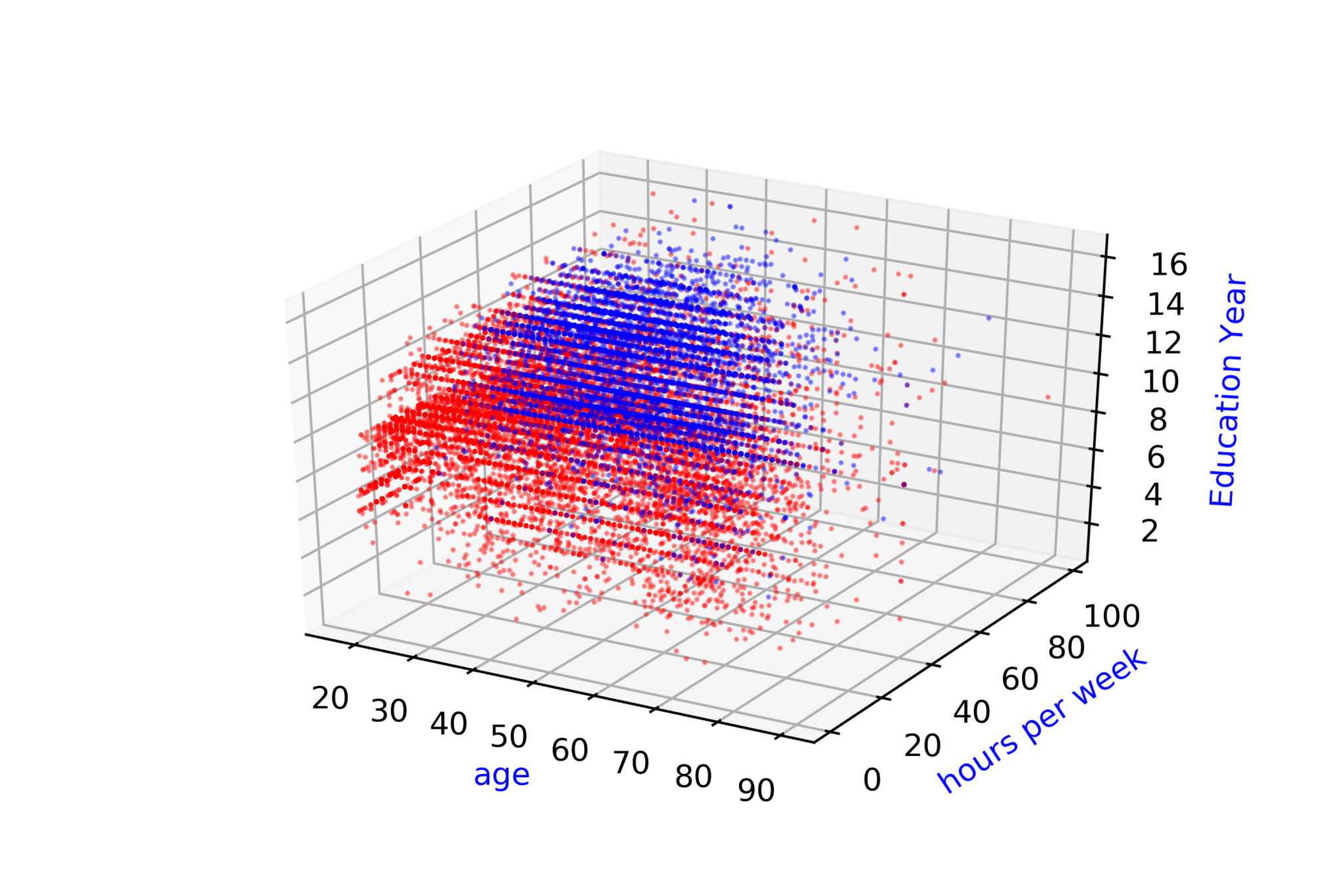
Adult Census Income\( ^{*} \)
Whether Annual Income of person \( \geq \) 50k or \( < \) 50k ?
| Age |
| 90 |
| 54 |
| 74 |
| 45 |
| hour/week |
| 40 |
| 40 |
| 20 |
| 35 |
| Education year |
| 9 |
| 4 |
| 16 |
| 16 |
| Income |
| 0 |
| 0 |
| 1 |
| 1 |
\( \hat{y} = \hat{f}(x_1, x_2, .... ,x_{14}) \)
\( \hat{income} = \hat{f}(age,hour, ...,education) \)
Modeling Complex Relations
Are such complex functions seen in most real world examples ?
(c) One Fourth Labs
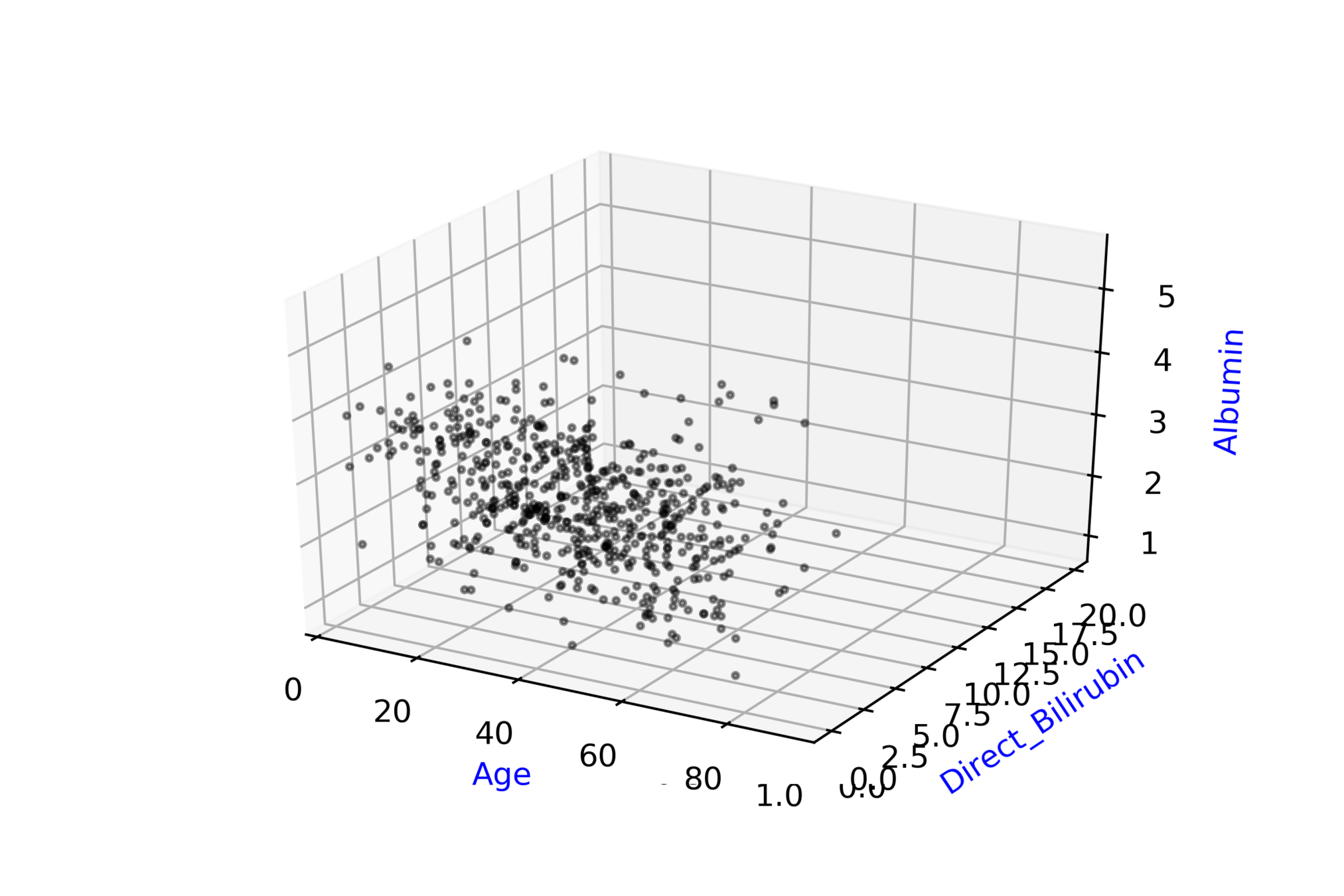
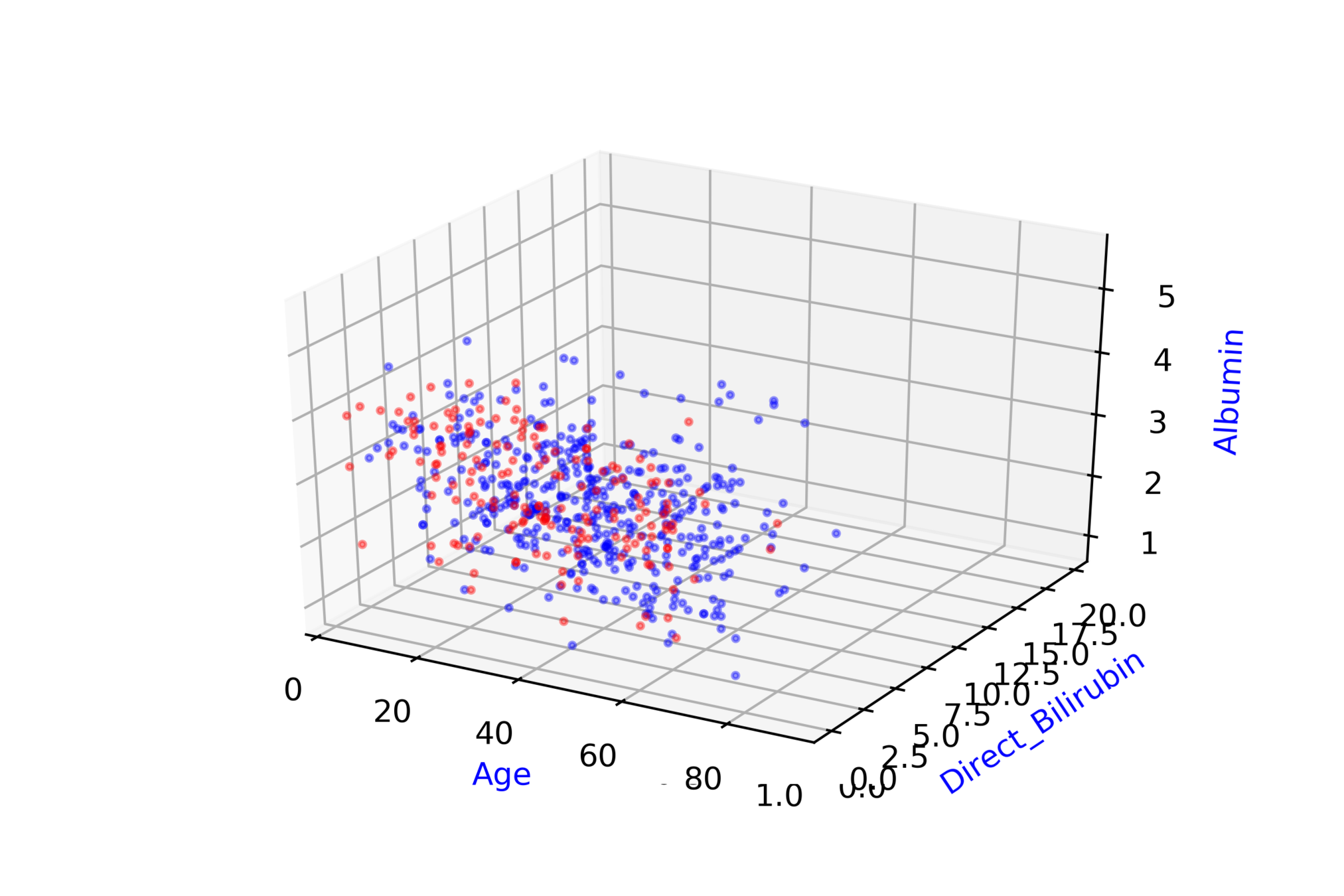
Indian Liver Patient Records\( ^{*} \)
whether person needs to be diagnosed or not ?
| Age |
| 65 |
| 62 |
| 20 |
| 84 |
| Albumin |
| 3.3 |
| 3.2 |
| 4 |
| 3.2 |
| T_Bilirubin |
| 0.7 |
| 10.9 |
| 1.1 |
| 0.7 |
| D |
| 0 |
| 0 |
| 1 |
| 1 |
\( \hat{y} = \hat{f}(x_1, x_2, .... ,x_{10}) \)
\( \hat{D} = \hat{f}(Age, Albumin, .... ,T\_Bilirubin) \)
Modeling Complex Relations
Are such complex functions seen in most real world examples ?
(c) One Fourth Labs
*https://www.kaggle.com/c/titanic/data
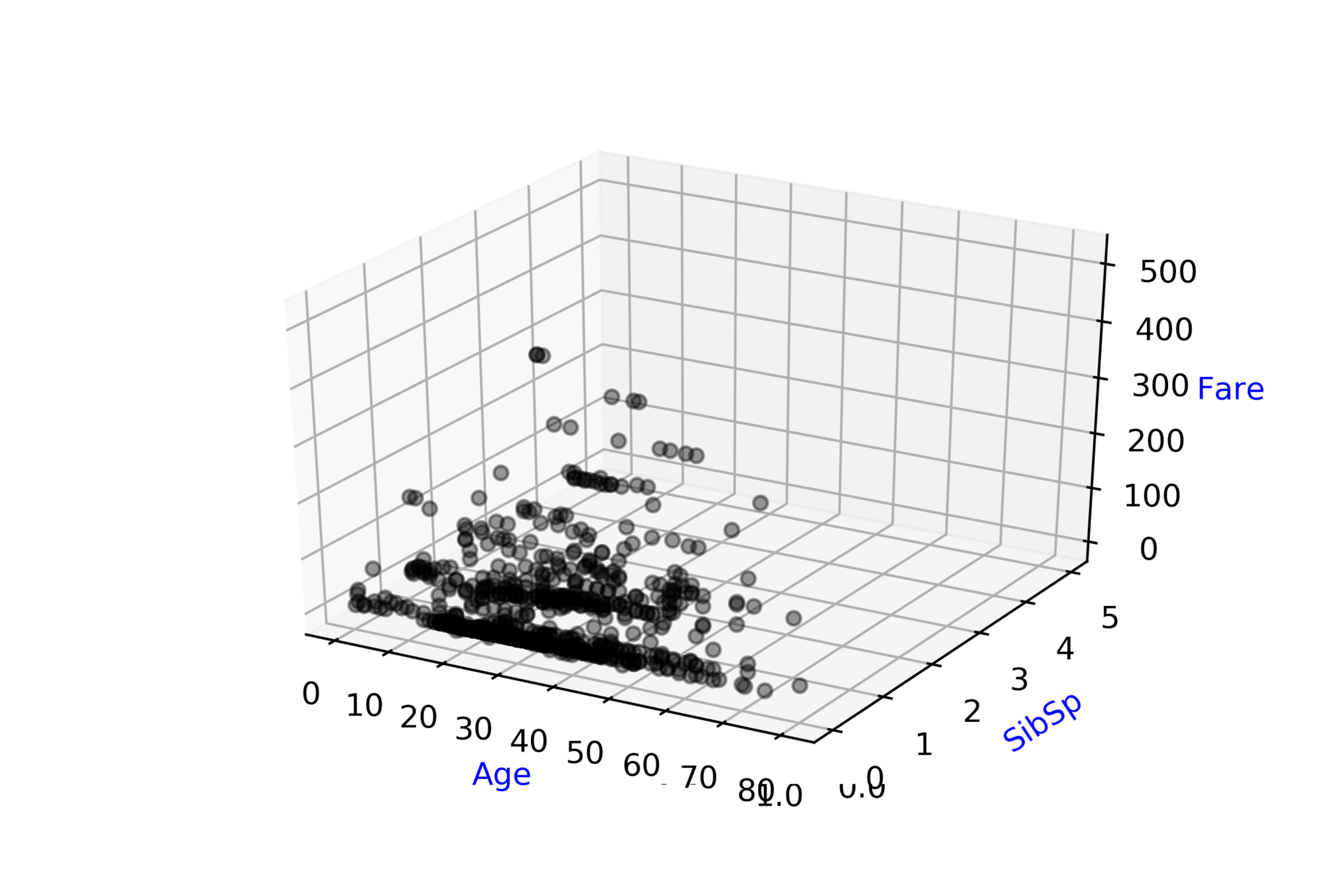
Titanic: Machine Learning from Disaster\( ^{*} \)
Predict survival on the Titanic
| Ticket class |
| 93.85 |
| -141.22 |
| -65.2 |
| 142.4 |
| # of siblings |
| 83.81 |
| -81.79 |
| -76.33 |
| 137.03 |
| Fare |
| 20.1 |
| -52.28 |
| -76.23 |
| 93.65 |
| Survived ? |
| 0 |
| 1 |
| 0 |
| 1 |
\( \hat{y} = \hat{f}(x_1, x_2, .... ,x_{9}) \)
\( \hat{D} = \hat{f}(ticket\_class, fare, .... ,age) \)
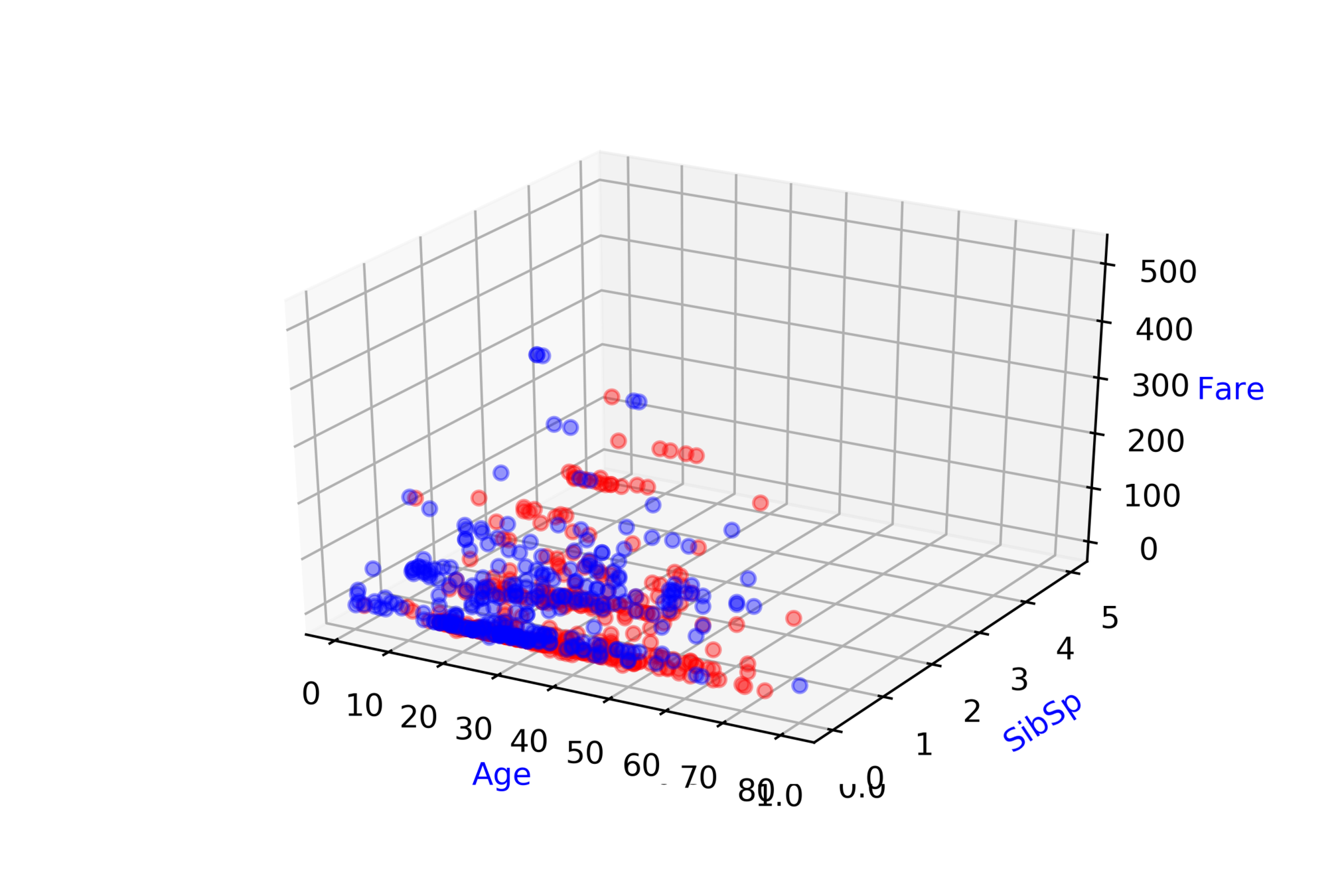
Modeling Complex Relations
How do we even come up with such complex functions ?
(c) One Fourth Labs
Class 1
Class 1
Class 1
Class 2
Class 2
Class 2
Class 1 : \( y^2 - x^2 + x^3/8 - y^3/6 > 0 \)
Class 2 : \( y^2 - x^2 + x^3/8 - y^3/6 \leq 0 \)
Class 1 : \( x^2*y + y^3*x > 0 \)
Class 2 : \( x^2*y + y^3*x \leq 0\)
Class 1: \( y - x*sin(x) > 0 \)
Class 2 : \( y - x*sin(x) \leq 0 \)
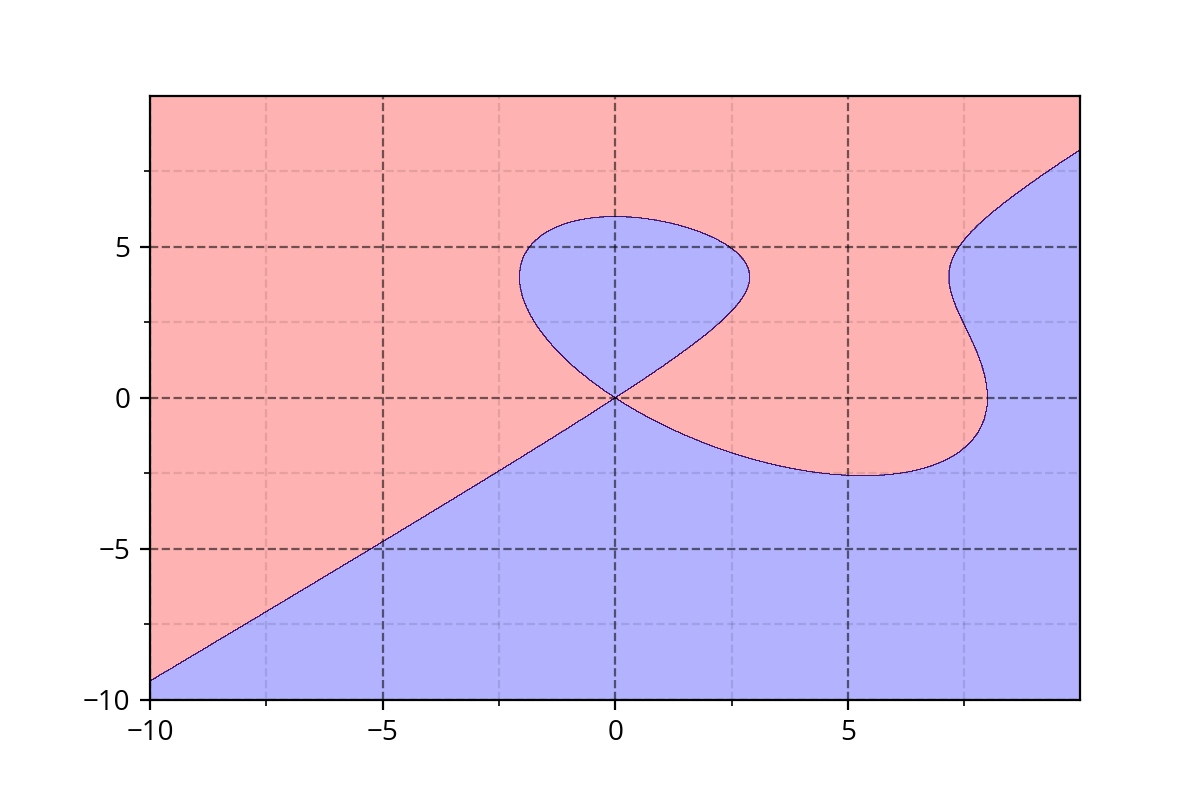
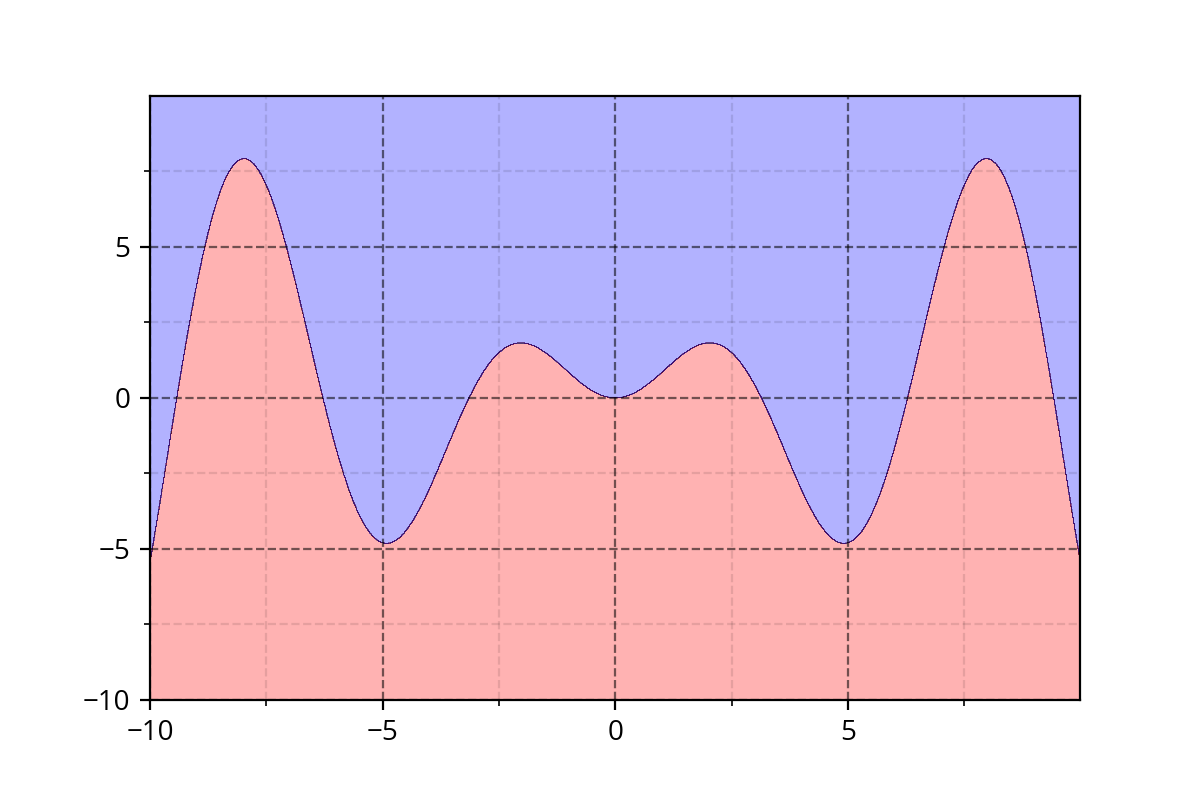
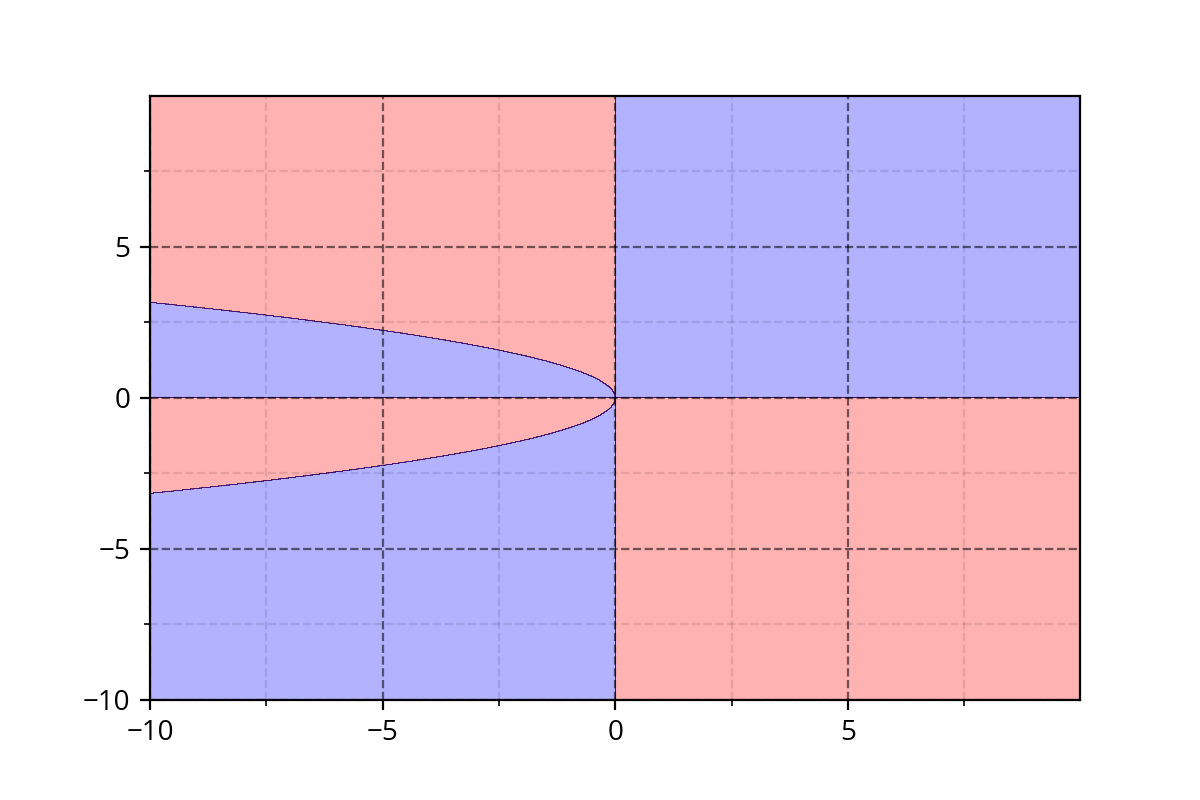
It's hard to come up with such functions. We need a simple approach!
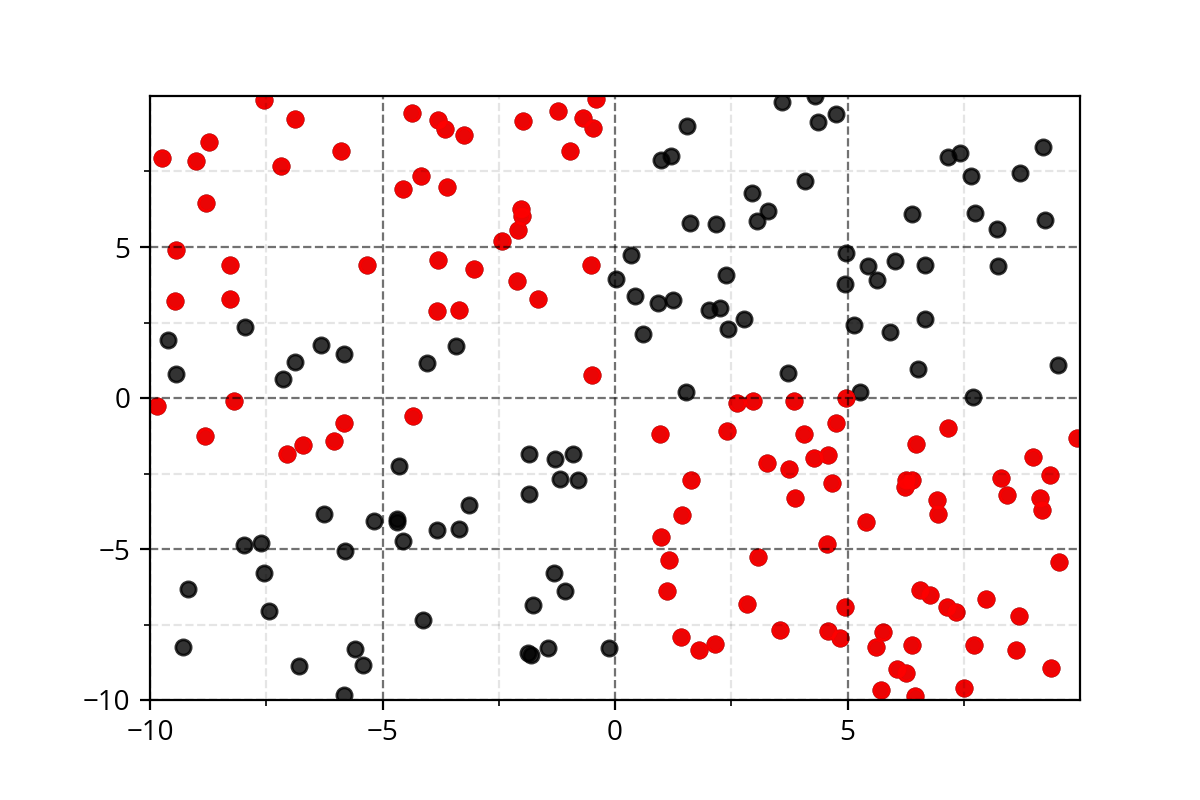
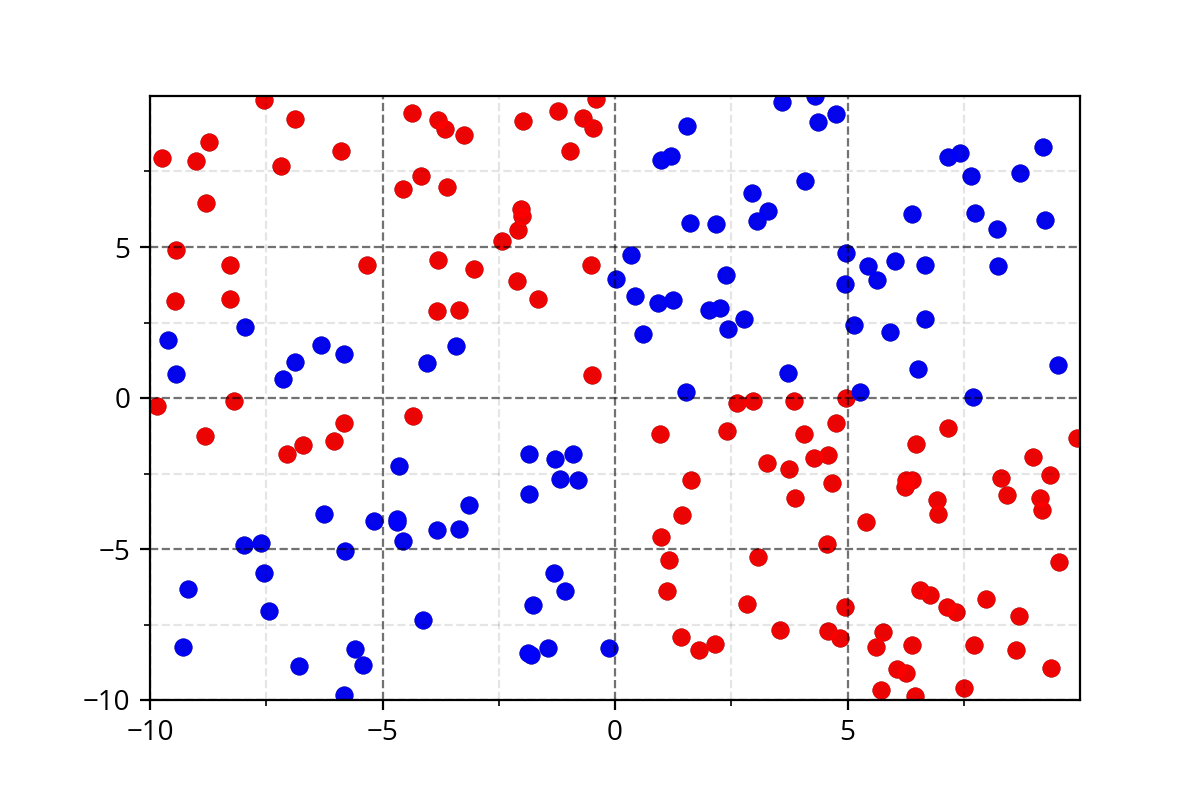
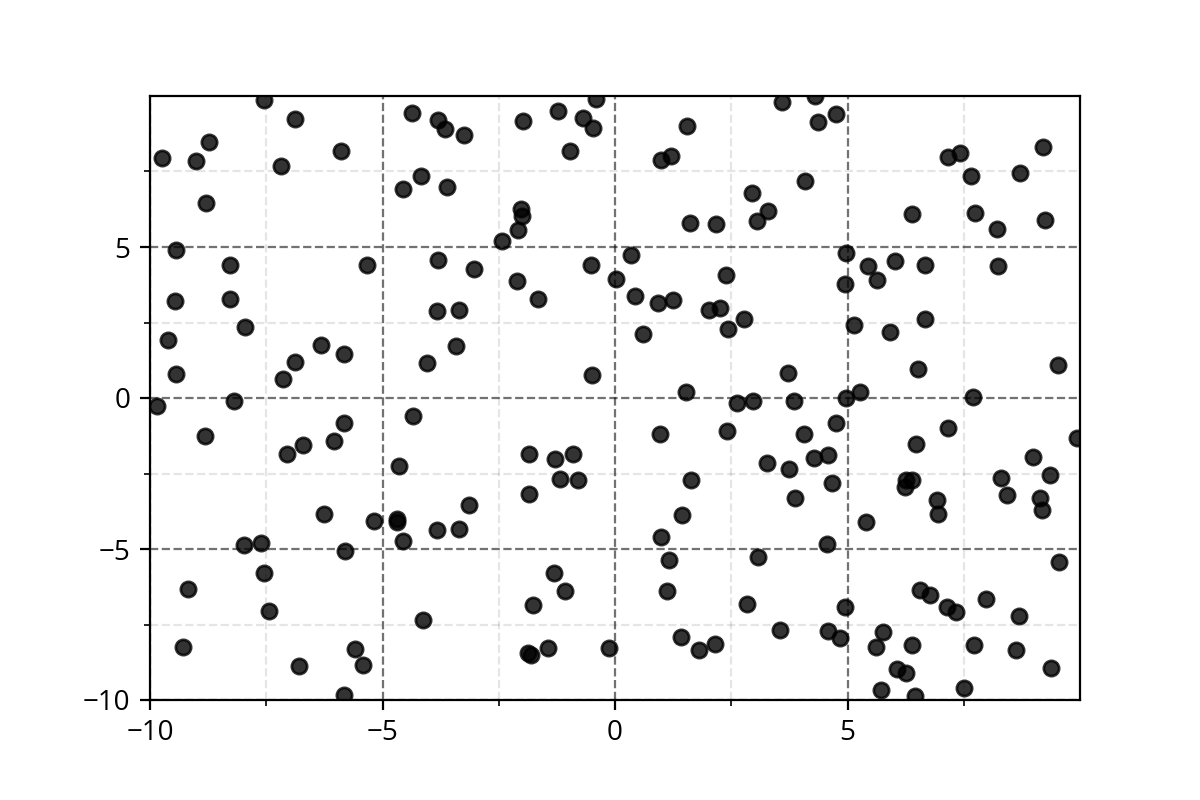
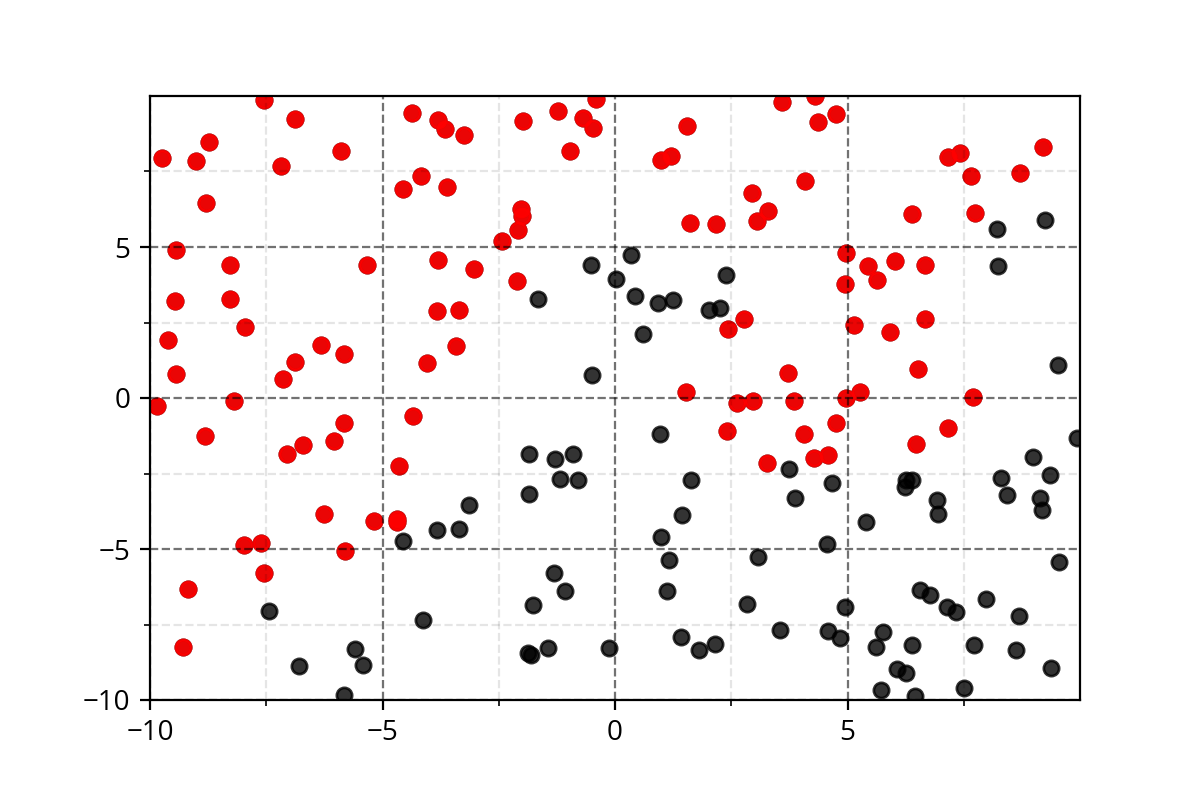
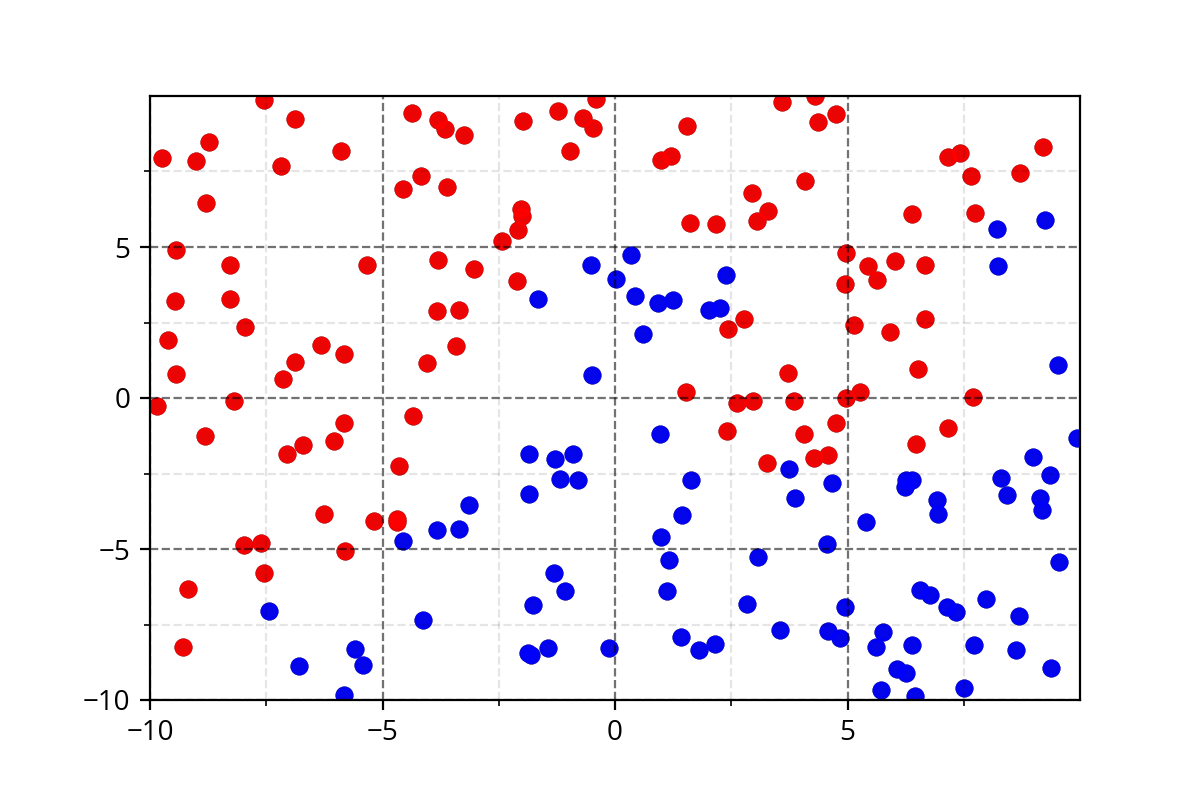
Modeling Complex Relations
How do we even come up with such complex functions ?
(c) One Fourth Labs
Class 1
Class 1
Class 1
Class 2
Class 2
Class 2
Modeling Complex Relations
How do we even come up with such complex functions ?
Class 1
Class 2
\( f(x_1,..,x_n) = \frac{1}{1+e^{-(w_1*x_1 + ... + w_n*x_n + b)}} \)
\( f(\bold{x},\bold{w}) = \frac{1}{1+e^{-(w*x + b)}} \)
\(w_1\)
\(w_n\)
\(x_n\)
\(x_1\)
\( f(\bold{x},\bold{w}) \)
\(x_1\)
\(x_n\)
\(\bold{h}\)
Modeling Complex Relations
How do we even come up with such complex functions ?
Class 1
Class 1
Class 1
Class 2
Class 2
Class 2
\( f(x_1,..,x_n) = \frac{1}{1+e^{-(w_1*x_1 + ... + w_n*x_n + b)}} \equiv \)
\( f(\bold{x},\bold{w}) = \frac{1}{1+e^{-(w*x + b)}} \equiv \)
(c) One Fourth Labs
Take-aways
How to distribute your work through the six jars?
(c) One Fourth Labs
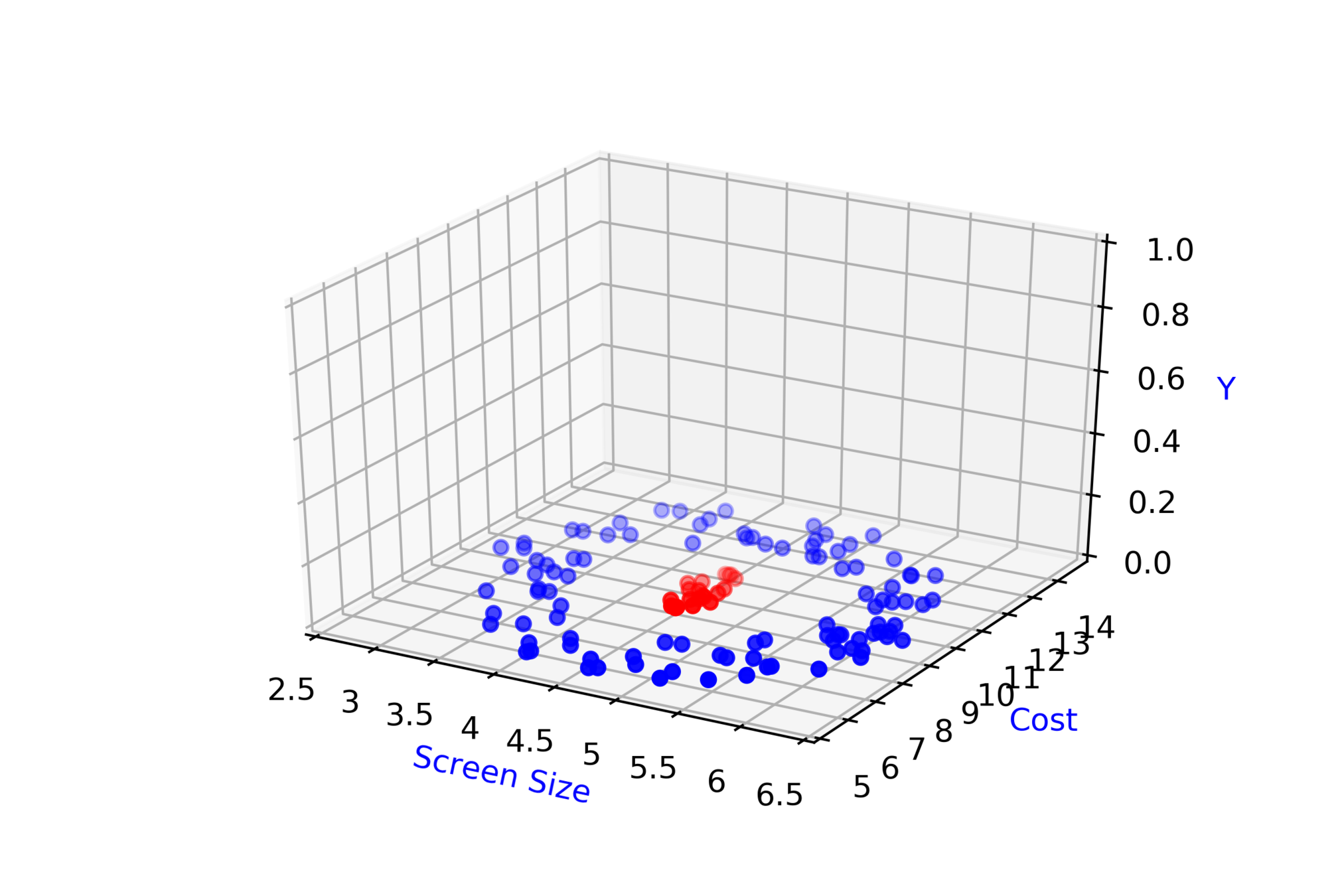
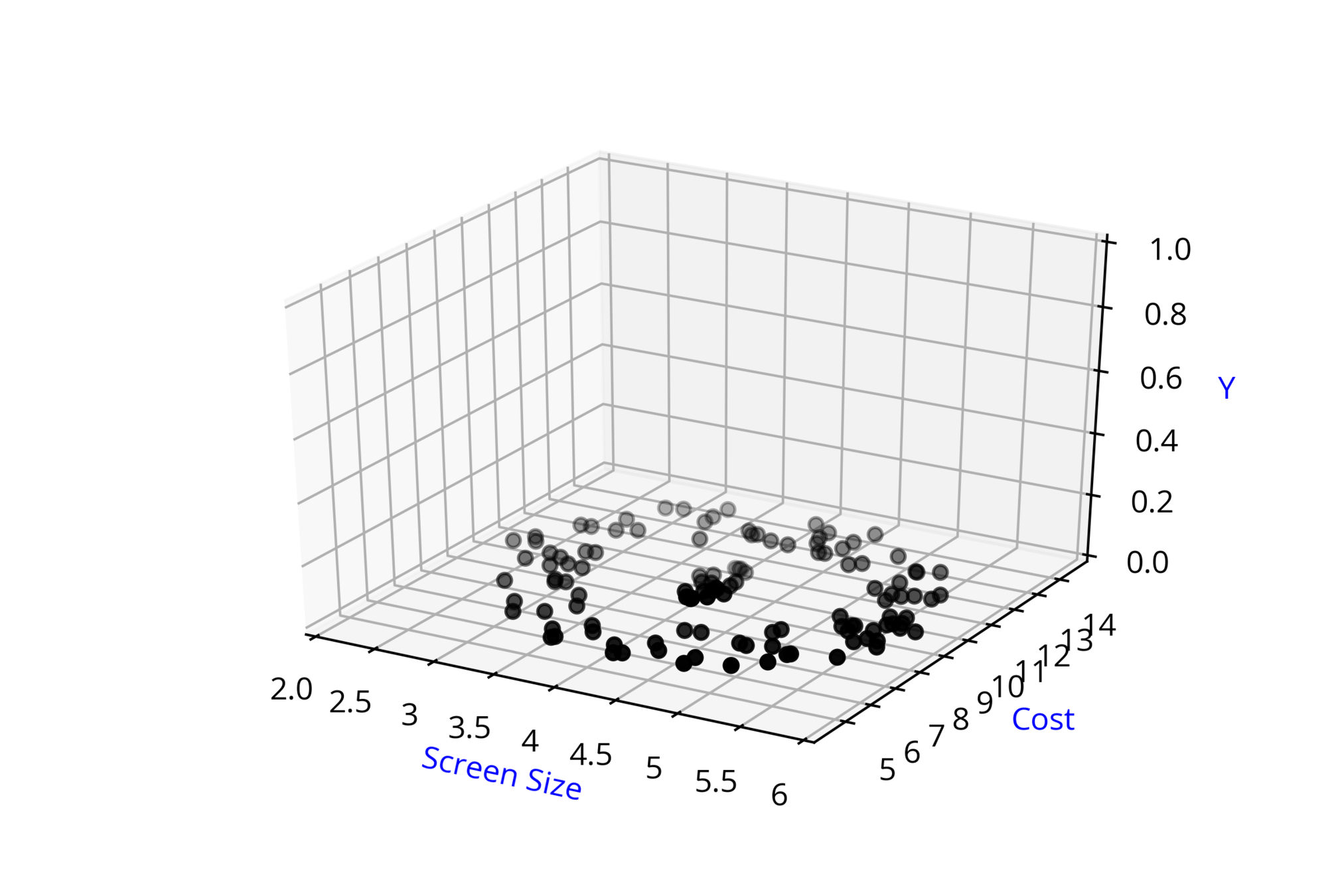
\( \in \mathbb{R} \)
loss = \sum_i (y_i-\hat{y_i})^2
Accuracy=\frac{\text{Number of correct predictions}}{\text{Total number of predictions}}
Loss
Model
Data
Task
Evaluation
Learning
Real inputs
\( w = w + \eta \frac{\partial L}{\partial w} \)
\( b = b + \eta \frac{\partial L}{\partial b} \)
Classification
Take-aways
What was all this leading up to ?
(c) One Fourth Labs
Accuracy
Data
\( w = w + \eta \frac{\partial L}{\partial w} \)
\( b = b + \eta \frac{\partial L}{\partial b} \)
Task
Model
Loss
Learning
Evaluation
1.8 Final Draft
By Shubham Patel
