COMP2521
Data Structures & Algorithms
Week 5.2
Graph Implementations
Author: Hayden Smith 2021
In this lecture
Why?
- Different graph implementations have different pros and cons, and we should try and understand the difference
What?
- Array of edges graph
- Adjacency Matrix graph
- Adjacency List graph
Properties of Graphs
Terminology: |V| and |E| (cardinality) normally written just as V and E
A graph with V vertices has at most V(V - 1) / 2 edges
The ratio E:V can vary considerably:
- If E is closer to V^2, the graph is dense
- If E is closer to V, the graph is sparse
Thinking about these things may help us decide on an appropriate data structure
Graph Representations
There are many ways to represent the same graph. E.G. The same graph could be represented these ways:
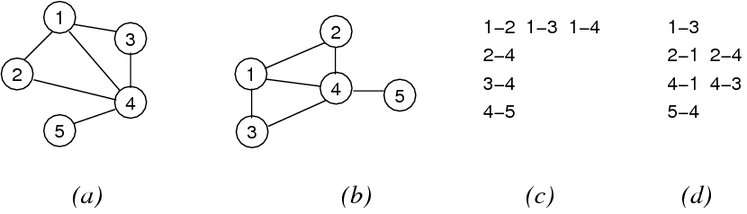
Graph Representations
There are 3 key different graph implementations we will discuss:
Array of Edges
Explicit representation as list of (v,w) vertex pairs
Adjacency Matrix
Edges defined by presence value in V*V matrix
Adjacency List
Edges defined by entries in array of V lists
Array-of-edges
Stored as an array of Edges (i.e. array of vertex pairs)
- Space efficient
- Adding/deleting: Mildly complex
- Lookup: Mildly complex
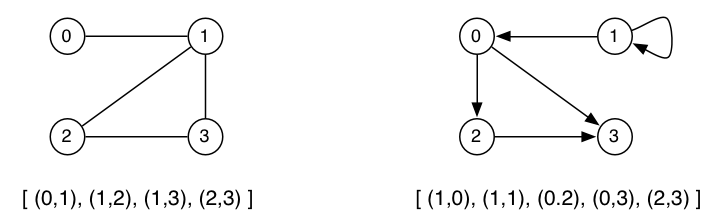
For directed graphs, the ordering of vertices within an edge pair denote direction
Array-of-edges Implementation
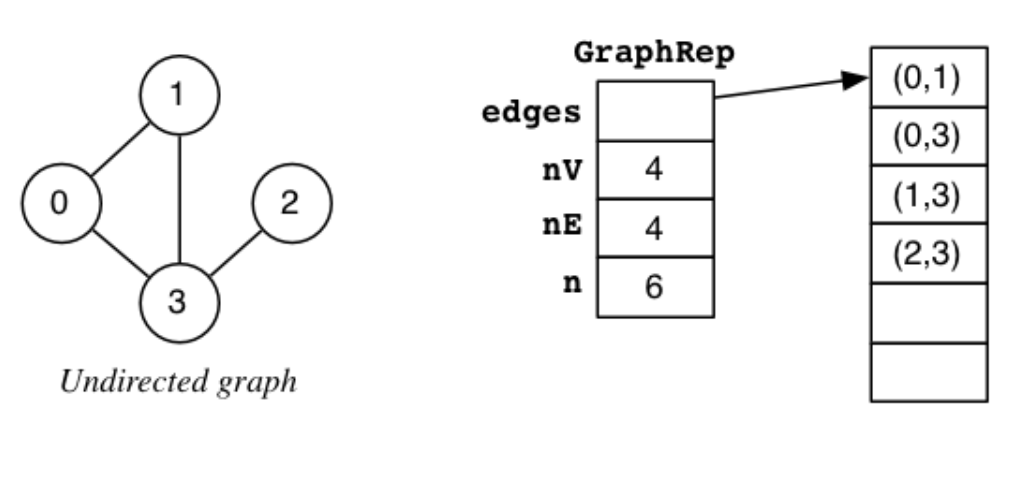
typedef struct GraphRep {
Edge *edges; // array of edges
int nV; // #vertices (numbered 0..nV-1)
int nE; // #edges
int n; // size of edge array
} GraphRep;Array-of-edges Pseudocode
newGraph(V):
g = new Graph with V verticies
g.nV = V // #vertices (numbered 0..V-1)
g.nE = 0 // #edges
allocate enough memory for g.edges[]
return ginsertEdge(g,(v,w)):
i=0
while i < g.nE ∧ g.edges[i] ≠ (v,w):
i = i + 1
if i = g.nE: // (v,w) not found
g.edges[i] = (v,w)
g.nE = g.nE + 1removeEdge(g,(v,w)):
i = 0
while i < g.nE ∧ g.edges[i] ≠ (v,w):
i = i + 1
if i < g.nE: // (v,w) found
g.edges[i] = g.edges[g.nE-1]
g.nE = g.nE - 1showEdges(g):
for all i=0 to g.nE-1:
(v,w) = g.edges[i]
print v"—"w
Array-of-edges Implementation
Full implementation in Graph-array-edges.c
Array-of-edges, Cost Analysis
- Storage: O(E)
-
Operations:
- Initialisation: O(1)
- Insert edge: O(E)
- Delete edge: O(E)
- Search: O(E)
-
Other factors:
- If array is full on insert, realloc - still O(E) amortized
- Maintaining edges in order will allow for O(log(E)) binary search lookup
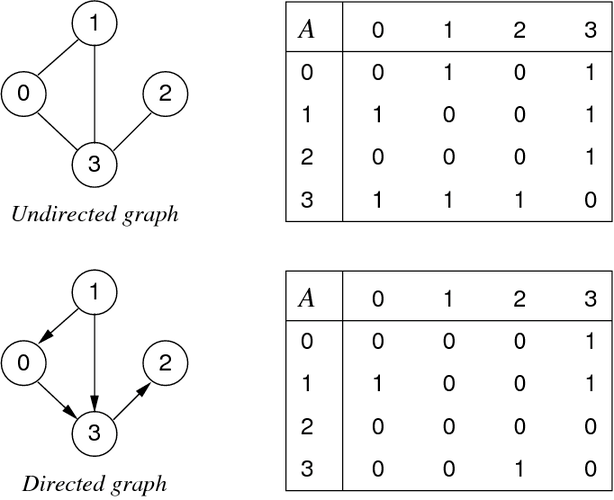
Adjacency Matrix
Stored as a 2D array (i.e. table) of edges. Easy to implement. Not memory efficient for sparse graphs.
For undirected graphs, the table is a mirror about the diagonal
Adjacency Matrix Implementation

typedef struct GraphRep {
int **edges; // adjacency matrix
int nV; // #vertices
int nE; // #edges
} GraphRep;Adjacency Matrix Pseudocode
newGraph(V):
g.nV = V // #vertices (numbered 0..V-1)
g.nE = 0 // #edges
allocate memory for g.edges[][]
for all i,j=0..V-1:
g.edges[i][j] = 0 // false
return ginsertEdge(g,(v,w)):
if g.edges[v][w] = 0: // (v,w) not in graph
g.edges[v][w]=1 // set to true
g.edges[w][v]=1
g.nE=g.nE+1
removeEdge(g,(v,w)):
if g.edges[v][w] ≠ 0: // (v,w) in graph
g.edges[v][w]=0 // set to false
g.edges[w][v]=0
g.nE=g.nE - 1showEdges(g):
for all i=0 to g.nV-1:
for all j=i+1 to g.nV-1:
if g.edges[i][j] ≠ 0 then
print i"—"j
Adjacency Matrix Implementation
Full implementation in Graph-adj-matrix.c
Adjacency Matrix, Cost Analysis
-
Storage: O(V^2)
- If the graph is sparse, most space is wasted
-
Operations:
- Initialisation: O(V^2)
- Insert edge: O(1)
- Delete edge: O(1)
- Search: O(1)
-
Other factors:
- For undirected graphs, the matrix is repeated about a diagonal axis. We can have a coefficient improvement in time complexity if we only store on one half of the diagonal
Adjacency List
Stored as an array of linked lists. Each element of the array corresponds to a vertex, each node on that linked list is an edge connected to that vertex.
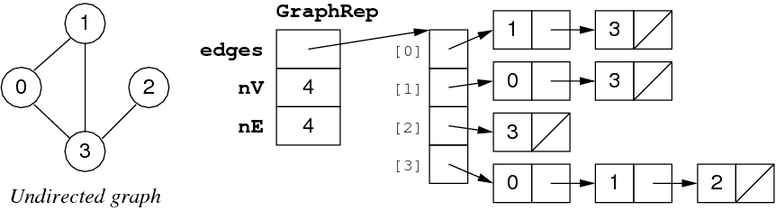
Adjacency List Implementation
typedef struct GraphRep {
Node **edges; // array of lists
int nV; // #vertices
int nE; // #edges
} GraphRep;
// Assumes we also have
typedef struct Node {
Vertex v;
struct Node *next;
} Node;
// with operations inLL, insertLL, deleteLL, freeLL
Adjacency List Pseudocode
newGraph(V):
g.nV = V // #vertices (numbered 0..V-1)
g.nE = 0 // #edges
allocate memory for g.edges[]
for all i=0..V-1:
g.edges[i]=newList() // empty list
return ginsertEdge(g,(v,w)):
if not ListMember(g.edges[v],w):
// (v,w) not in graph
ListInsert(g.edges[v],w)
ListInsert(g.edges[w],v)
g.nE=g.nE+1
removeEdge(g,(v,w)):
if ListMember(g.edges[v],w):
// (v,w) in graph
ListDelete(g.edges[v],w)
ListDelete(g.edges[w],v)
g.nE=g.nE-1showEdges(g):
for all i=0 to g.nV-1:
for all v in g.edges[i]:
if i < v:
print i"—"v
Adjacency List Implementation
Full implementation in Graph-adj-list.c
Adjacency List, Cost Analysis
- Storage: O(V + E)
-
Operations:
- Initialisation: O(V)
- Insert edge: O(V)
- Delete edge: O(V)
- Search: O(V)
-
Other factors:
- Sorting vertex lists has no benefit
Comparison of Graph Implementations
Terminology: |V| and |E| (cardinality) normally written just as V and E
A graph with V vertices has at most V(V - 1) / 2 edges
| Array of edges | Adjacency Matrix | Adjacency List | |
|---|---|---|---|
| Space usage | E | V^2 | V + E |
| Initialise | 1 | V^2 | V |
| Insert edge | E | 1 | V |
| Remove edge | E | 1 | V |
| isPath(x,y) | E*log(V) | V^2 | V + E |
| Copy graph | E | V^2 | V + E |
| Destroy Graph | 1 | V | V + E |
| Search | E | 1 | V |
Copy of COMP2521 21T2 - 5.2 - Graph Implementations
By Sim Mautner
Copy of COMP2521 21T2 - 5.2 - Graph Implementations
- 799



