Effet Faraday
Description du phénomène
Type d'anisotropie
Visualisation du phénomène
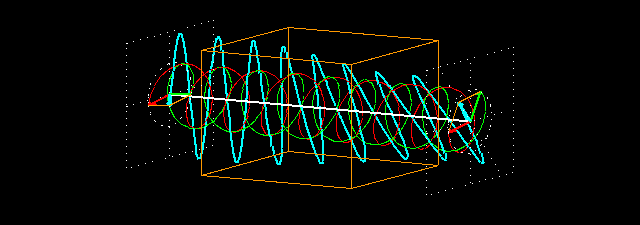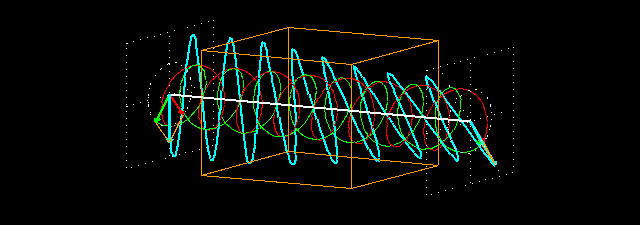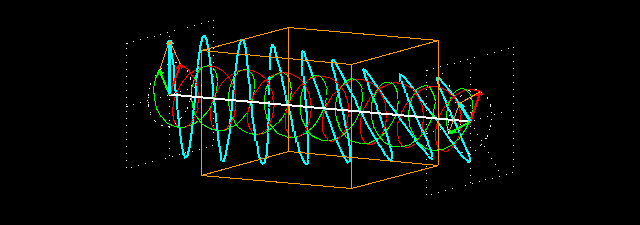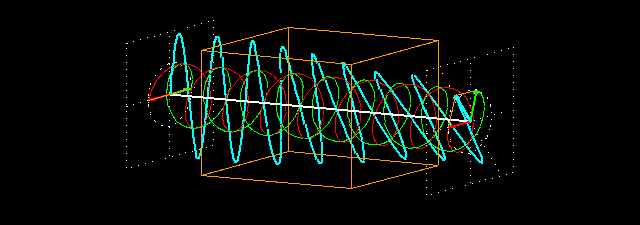
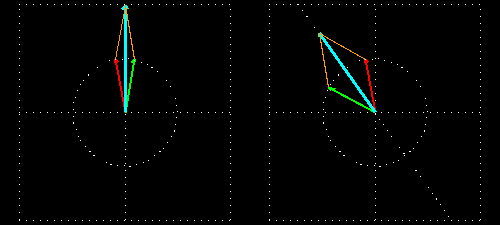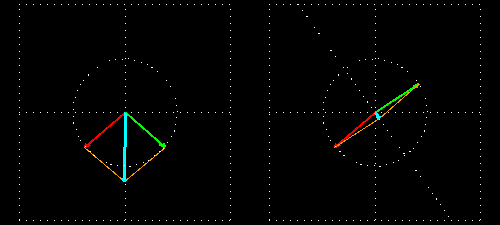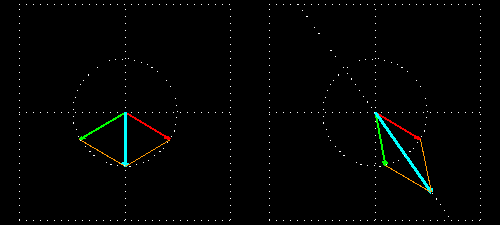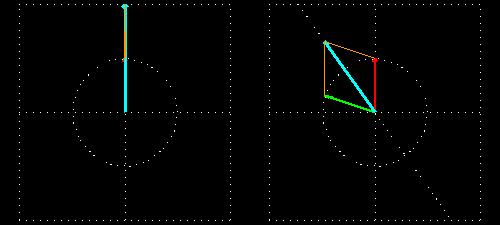
Description du phénomène
Relation de Verdet
\alpha =\nu l B
Résumé
Rotation du plan de polarisation
Indices différents pour deux ondes circulaires
Quelques matériaux
Les exemples de la vie "courante"
Grenats ferrimagnétiques
Les matériaux présentant l'effet Faraday
Orthoferrites
Cristaux rhomboédriques
Description mathématique
Shit about to get real"
Hypothèses
Les deux ondes circulaires se propagent avec deux indices différents :
n_G
n_D
, pour l'onde circulaire gauche
, pour l'onde circulaire droite
Hypothèses
On écrit la polarisation rectiligne comme superposition de deux ondes circulaires de sens inverse et de même amplitude :
{u}_{1}=\frac{\mathrm{exp}\left(i\alpha \right)}{\sqrt 2} \left( \begin{array}{c}1\\ +i\end{array} \right)
{u}_{2}=\frac{\mathrm{exp}\left(i \beta \right)}{\sqrt 2} \left( \begin{array}{c}1\\ -i\end{array} \right)
On définit aussi :
\sigma =\beta +\alpha \text{ et }\delta =\beta -\alpha
Onde rectiligne résultante
Ainsi l'onde rectiligne s'écrit :
u=\sqrt{2} \,\mathrm{exp}\left(\frac{i\sigma }{2}\right)\left(\begin{array}{c}\mathrm{cos}\left(\frac{\delta }{2}\right)\\ \mathrm{sin}\left(\frac{\delta }{2}\right)\end{array}\right)
C'est une onde polarisée rectilignement d'angle
\frac{\delta}{2}
Retard pour les ondes circulaires
Les deux ondes accumulent un retard différent !
En sortie, en z = L :
L'onde gauche fait un angle :
L'onde droite fait un angle :
2 \pi \nu_0 \left( t- \frac{n_G L}{c}\right) - \alpha
2 \pi \nu_0 \left( t- \frac{n_D L}{c}\right) + \alpha
Ainsi, en utilisant le même raisonnement, l'onde résultante fera avec (Ox) l'angle :
\frac{\pi \nu_0}{c} \left( n_D - n_G \right) l
Applications
Modulateurs d'intensité
Stockage magnéto-optique
Isolateur optique
Applications
Applications
Isolateur optique
Présentation Lumière Polarisée - effet Faraday
By Claude-Alban RANÉLY-VERGÉ-DÉPRÉ
