Системы типов

в двух словах

Вячеслав Шебанов

Disclaimer

Зачем нужны типы?

Слово (Word)

1011010001001010100011110101010

Слова имеют смысл

Но этот смысл задается внешней системой

Типы появляются естественным образом

лорд Бертран Рассел

“Пусть в некой деревне живёт  брадобрей, который бреет всех жителей деревни, которые не бреются сами, и только их.

 

Бреет ли брадобрей сам себя?

Парадокс Брадобрея

Теория типов Рассела

Примитивные типы


let isDone: boolean = false;


let someNumber: number = 10;

Зачем нужны типы?

Чтобы в вашей программе не было парадоксов (ошибок)

Давид Гильберт

Entscheidungsproblem

Проблема разрешимости

Можем ли мы, описав некое утверждения специальным образом, ответить на вопрос с помощью общего метода является ли это утверждение истиной всегда

Алонзо Черч

λ-исчисление

  • x, y, a-z — переменная
  • M, N, A-Z — терм (выражение)
  • λx.M — абстракция (анонимная функция)
  • (M N) — применение (вызов функции)

λ-исчисление

(λx . x) z
(λx . x) z → z
(λx. x) (λx. x)
(λx. x) (λx. x) → (λx. x)

Identity function

function identity(x) {
  return x;
}

А как же типы?

Простое типизированное λ-исчисление

λ→

(λx:Bool . x):Bool

Simply-Typed Lamda Calculus

function identity(x: number): number {
  return x;
}
(λx:Int y:Int . x * y): Int
function mult(x: number, y: number): number {
  return x * y;
}

Полиморфизм

function saySomething(cat: Cat) {
  return 'Meow';
}

function saySomething(dog: Dog) {
  return 'Woof';
}
function saySomething(cat: Cat) {
  return 'Meow';
}

function saySomething(dog: Dog) {
  return 'Woof';
}

> saySomething(cat);
"Meow"

> saySomething(dog);
"Woof"
function identity<T>(arg: T): T {
    return arg;
}

System F

Жирар 1972, Рейнольдс 1974

Абстракция на типах

λx:Bool . x

λX. λx:X. x

Абстракция на типах

id = λX. λx:X. x

Абстракция на типах

|> id : ∀X. X → X

Абстракция на типах

(λX. λx:X. x) Bool

Абстракция на типах

λx:Bool. x

Дженерики в Go

func Print[T any](s []T) {
	for _, v := range s {
		fmt.Println(v)
	}
}

Print[int](arrayOfInts)

*вы находитесь здесь*

Расширения

(Records)

struct Person
{
    char name[50];
    int age;
    float salary;
};

Как понять, что в самой системе типов нет ошибок?

Soundness

  • Прогресс
  • Сохранение типов

Прогресс

(λx:Int y:Int . x * y) a b

Если a и b это Int

Сохранение типов

(λx:Int y:Int . x * y) a b 
→ 
a * b

Когда добавляешь новую фичу в язык

Java and Scala’s Type Systems are Unsound 

(2016 Amin, Tate)

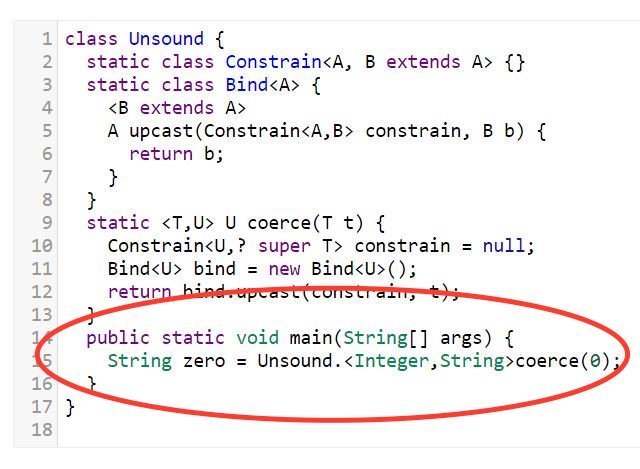
Вернемся в 1937

Алан Тьюринг

Проблема останова

Даны описание процедуры и её начальные входные данные, требуется определить, завершится ли когда-либо выполнение процедуры с этими данными.

Тезис Черча-Тьюринга

Любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга

Тьюринг-полнота

Строгая нормализация

Простое типизированное лямбда-исчисление

System F

Тотальность

Тотальной называется такая функция, которая гарантированно завершается за конечное количество шагов и определена на всех разрешенных входных параметрах

Тотальность

Хенк Барендрехт

λ-куб

Можно типизировать функции

function identity(x: Bool): Bool {
  return x;
}

Можно типизировать полиморфизм

function identity<T>(x: T): T {
  return x;
}

Можно использовать функции на уровне типов

Типы высшего рода (Higher Kinded Types) и семейства типов (Type Families) в Haskell

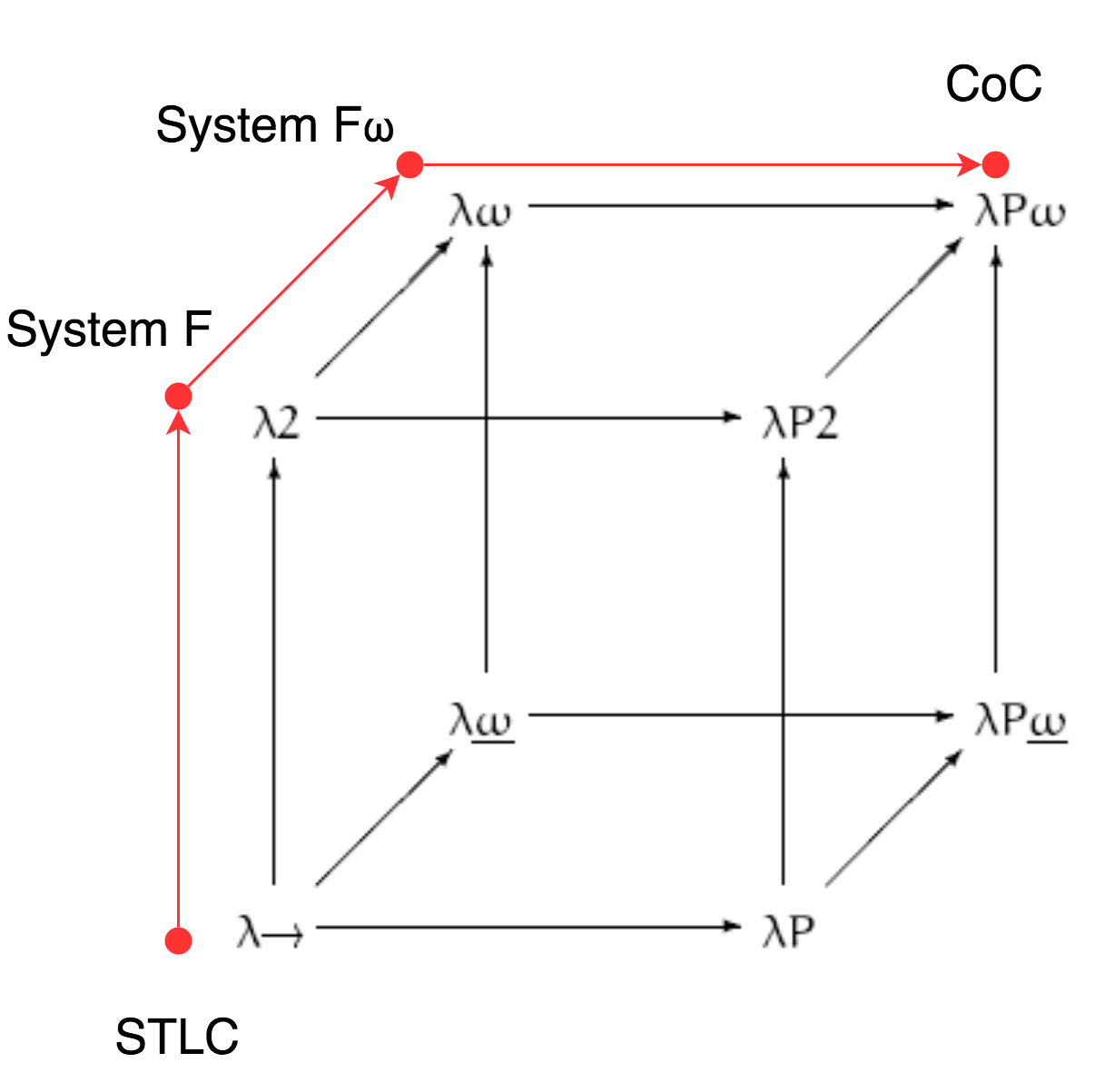
Можно использовать значения переменных на уровне типов

function random(n: Nat) : Fin<n> {
  return ...;
}

Хотите подробнее?

Задавайте вопросы после доклада!

Верификация ПО

Что это значит?..

Можно писать код без ошибок!

CompCert

Project Everest

Соответствие Карри-Говарда

Линейные типы

Продолжаем заимствования из логики

Линейные типы

let x = vec![1, 2, 3];
let y = x;           // NOTE: x moved here
println!("{:?}", x); // ERROR: use of moved value x
pritnln!("{:?}", y); // OK

Еще непонятнее

HoTT и Кубические типы

Послесловие

Ссылки

normal

Ссылки

hard

Ссылки

nightmare

Конец

Twitter: @thought_sync

Зависимые типы

за 5 минут

function zip<T1, T2>(list1: Array<T1>, list2: Array<T2>): Array<Pair<T1, T2>> {
    if (list1.length !== list2.length) {
		throw Error('Arrays lengths are not equal');
    }
    let result = [];
    for (let i = 0; i < list1.length; i++) {
        result[i] = pair(list1[i], list2[i]);
    }

    return result;
}
function zip<T1, T2>(list1: Array<T1>, list2: Array<T2>)
Array<Pair<T1, T2>>
if (list1.length !== list2.length) {
  throw Error('Arrays lengths are not equal');
}
let result = [];
for (let i = 0; i < list1.length; i++) {
    result[i] = pair(list1[i], list2[i]);
}

return result;

Более точный тип

Vect<T, n>

T — тип элемента

n — кол-во элементов

function zip<T1, T2>(v1: Vect<T1, n>, v2: Vect<T2, n>): Vect<Pair<T1, T2>, n> {
    let result = [];
    for (let i = 0; i < n; i++) {
        result[i] = pair(v1[i], v2[i]);
    }
    return result;
}
function zip<T1, T2>(v1: Vect<T1, n>, v2: Vect<T2, n>)
Vect<Pair<T1, T2>, n>

Откуда берутся вектора?

function vectToList<T>(list: Array<T>) : DPair(n: Nat, Vect<T, n>) {
    return dpair(list.length, toVect(list));
}
function vectToList<T>(list: Array<T>)
DPair(n: Nat, Vect<T, n>)

Зависимая пара

return dpair(list.length, toVect(list));

Системы типов в двух словах v2

By Slava Shebanov

Made with Slides.com

Системы типов в двух словах v2

  • 1,375

More from Slava Shebanov