Прагматичные зависимые типы

Обо мне

main :: IO ()
main = putStrLn "Hello, world!"

Это не туториал

Зависимые типы

zipWith : (a -> b -> c) -> Vect n a -> Vect n b -> Vect n c
zipWith f [] [] = []
zipWith f (x :: xs) (y :: ys) = f x y :: zipWith f xs ys
AdderType : (numargs : Nat) -> Type -> Type
AdderType Z numType = numType
AdderType (S k) numType = (next : numType) -> AdderType k numType

adder : Num numType => (numargs : Nat) -> numType -> AdderType numargs numType
adder Z acc = acc
adder (S k) acc = \next => adder k (next + acc)

Глава 6.2.1  TDD with Idris

Тотальность и страдания

Тотальная функция

sum : Int -> List Int -> Int
sum a [] = a
sum a (x :: xs) = sum (a + x) xs

(Не)Тотальная функция

%default total

mutual
  data TLSExpr : Type where
    MkTLSExprType : (type : TLSTypeExpr) -> TLSExpr

  data TLSTypeExpr : Type where
    MkTLSTypeExpr : (type : Int) -> (children : List TLSExpr) -> TLSTypeExpr
    MkTLSTypeVar : (ref : Int) -> TLSTypeExpr

  Show TLSExpr where
    show (MkTLSExprType type) = show type

  Show TLSTypeExpr where
    show (MkTLSTypeExpr type children) = "Type Ref (" ++ (show type) ++ ") " 
                                         ++ (show children)
    show (MkTLSTypeVar ref) = "TypeVar #" ++ (show ref)

(Не)Тотальная функция

11 |   Show TLSExpr where

   |   ~~~~~~~~~~~~

Main.TLSExpr implementation of Prelude.Show.Show is possibly not total due to recursive path Prelude.Show.Main.TLSTypeExpr implementation of Prelude.Show.Show, method show --> Prelude.Show.Main.TLSExpr implementation of Prelude.Show.Show, method show --> Prelude.Show.Main.TLSExpr implementation of Prelude.Show.Show, method show

test.idr:14:3-18:   |

14 |   Show TLSTypeExpr where   |   ~~~~~~~~~~~~~~~~

Main.TLSTypeExpr implementation of Prelude.Show.Show is possibly not total due to: Prelude.Show.Main.TLSExpr implementation of Prelude.Show.Show, method show

TLSExpr

TypeVar

Expr

Взаимная рекурсия

Верификация

Доказанная сортировка массива для разных языков:

Type Language

(https://core.telegram.org/mtproto/TL) 

boolFalse = Bool;
boolTrue = Bool;

TL:

Idris:

data Bool : Type where
  boolFalse : Bool
  boolTrue : Bool

vector {t:Type} n:Nat n*[t] = Vector t;
tuple {t:Type} {n:Nat} [t] = Tuple t n;

vectorInt v:(Vector Int) = VectorInt

user {n:Nat} first_name:string 
  second_name:string middle_name:n.0?string = User n;

userMiddle user:(User 1) = UserMiddle;

TLHydra

Ошибки новичка

public export
data hexFixedStr : (length : Nat) -> 
  (subject : StrList str) -> Type where

    hexStrEmpty : hexFixedStr 0 SNil

    hexNext : (symbol : Char) ->
              (prf : (isHexDigit symbol) = True) ->
              hexFixedStr ln str ->
              hexFixedStr (S ln) (SCons symbol str)

Полезные завтипы

sum : Fin a -> Fin b -> Fin (a + b)
zipWith : (a -> b -> c) -> Vect n a -> Vect n b -> Vect n c
zipWith f [] [] = []
zipWith f (x :: xs) (y :: ys) = f x y :: zipWith f xs ys

Тотальные парсеры

Parsec

Lightyear

Blodwen

Text.Parser

data Grammar : (tok : Type) -> 
  (consumes : Bool) -> Type -> Type where

Empty : (val : ty) -> Grammar tok False ty
Terminal : (tok -> Maybe a) -> Grammar tok True a
NextIs : (tok -> Bool) -> Grammar tok False tok
EOF : Grammar tok False ()
Fail : String -> Grammar tok c ty
Commit : Grammar tok False ()
SeqEat : Grammar tok True a -> Inf (a -> Grammar tok c2 b) ->
         Grammar tok True b
SeqEmpty : {c1, c2 : Bool} ->
           Grammar tok c1 a -> (a -> Grammar tok c2 b) ->
           Grammar tok (c1 || c2) b
Alt : {c1, c2 : Bool} ->
           Grammar tok c1 ty -> Grammar tok c2 ty ->
           Grammar tok (c1 && c2) ty
many : Grammar tok a -> Grammar tok (List a)
many p = option [] (do
  x <- p
  xs <- many p
  pure (x :: xs)
)

many : Grammar tok True a -> Grammar tok False (List a)
many p = option [] (do
  x <- p
  xs <- many p
  pure (x :: xs)
)

# int ? = Int;

parseBuiltin : Rule TLDeclaration
parseBuiltin = do name <- combinatorName
                  expect $ TLTokenChar '?'
                  expect $ TLTokenChar '='
                  type <- parseResultType
                  expect $ TLTokenChar ';'
                  pure $ BuiltInCombinator $ MkTLCombinator name [] type

Минусы

  • Почти полное отсутствие документации и примеров
  • Скорость работы
  • Примеры смотреть в Blodwen

tparsec

Инфраструктура

Профилировка

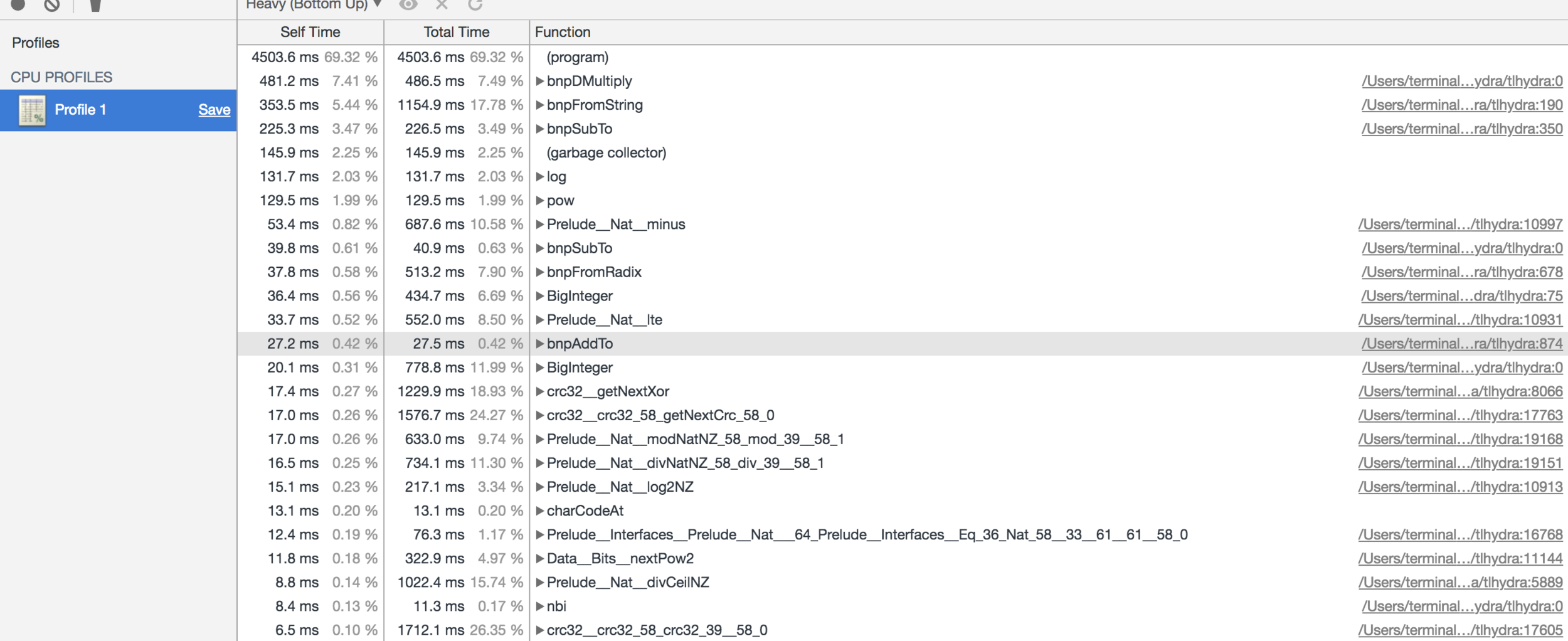
Не хватает

Редакторы

  • VS Code
  • Atom
  • Vim

Документация

  • Документация тут
  • Но лучше смотреть код

Будущее

Конец

Прагматичные зависимые типы

By Slava Shebanov

Made with Slides.com

Прагматичные зависимые типы

  • 2,231

More from Slava Shebanov