Extending active inference to other intrinsic motivations

Martin Biehl

  • focus on technical aspects of discrete version of active inference
  • clarify relations to
    • "standard" Bayesian agents
    • reinforcement learning
    • intrinsic motivations
  • assume free choice of internal dynamics of agent (unlike in the Markov blanket approach)

Preliminary remarks

  1. Formal framework for a Bayesian agent
    1. Perception-action loop
    2. Generative model
    3. Inference (obtaining a complete posterior)
    4. Action selection
  2. Active inference
  3. Some possible intrinsic motivations:
    1. Conditional entropy maximization
    2. Predictive information maximization
    3. Knowledge seeking
    4. Empowerment maximization
    5. Curiosity

Overview

1. Formal framework for a Bayesian agent

  1. Perception-action loop

Similar to reinforcement learning for POMDPs :

  • partially observable environment
  • unknown environment transition dynamics

But we assume no reward

\(E\) : Environment state

\(S\) : Sensor state

\(A\) : Action

\(M\) : Agent memory state

\(\newcommand{\p}{\text{p}} \p(e_0)\) : initial distribution

\(\newcommand{\p}{\text{p}}\p(s|e)\) : sensor dynamics

\(\newcommand{\p}{\text{p}}\p(m'|s,a,m)\) : memory dynamics

\(\newcommand{\p}{\text{p}}\p(a|m)\) : action generation

\(\newcommand{\p}{\text{p}}\p(e'|a',e)\) : environment dynamics

1. Formal framework for a Bayesian agent

  1. Perception-action loop

Assumptions :

  • constant environment and sensor dynamics given $$\newcommand{\p}{\text{p}}\p(e_{t_1}|a_{t_1},e_{t_1-1})=\p(e_{t_2}|a_{t_2},e_{t_2-1})$$ $$\newcommand{\p}{\text{p}}\p(s_{t_1}|e_{t_1})=\p(s_{t_2}|e_{t_2})$$
  • perfect agent memory :  $$\newcommand{\pt}{{\prec t}}m_t := (s_\pt,a_\pt) := sa_\pt \Rightarrow \newcommand{\p}{\text{p}}\p(m'|s,a,m) $$

1. Formal framework for a Bayesian agent

  1. Perception-action loop

Left to be specified:

  • action generation mechanism \(\newcommand{\p}{\text{p}} \p(a|m)\)
    • takes current sensor-action history \(m_t=sa_{\prec t}\) to generate new action \(a_t\)

 

1. Formal framework for a Bayesian agent

  1. Perception-action loop
  • in short, action generation mechanism \(\newcommand{\p}{\text{p}} \p(a|m)\) at each \(t\):
    • takes new sensor-action history \(m_t=sa_{\prec t}\)
    • uses a parameterized model,
    • infers its parameters / updates its beliefs
    • predicts consequences of actions,
    • selects action according to preferences / motivation

 

1. Formal framework for a Bayesian agent

  1. Perception-action loop

1. Formal framework for a Bayesian agent

2. Generative model

  • Internal to the agent
  • For parameters write \(\Theta=(\Theta^1,\Theta^2,\Theta^3)\)
  • \(\xi=(\xi^1,\xi^2,\xi^3)\) are fixed hyperparameters that encode priors over the parameters

1. Formal framework for a Bayesian agent

2. Generative model

Model split up into three parts:

  1. sensor dynamics model \(\newcommand{\q}{\text{q}}\newcommand{\hs}{\hat{s}}\q(\hat{s}|\hat{e},\theta)\)
  2. environment dynamics model \(\newcommand{\q}{\text{q}}\newcommand{\ha}{\hat{a}}\q(\hat{e}'|\ha,\hat{e},\theta)\)
  3. initial environment distribution \(\newcommand{\q}{\text{q}}\newcommand{\hs}{\hat{s}}\q(\hat{e}|\theta)\)

1. Formal framework for a Bayesian agent

2. Generative model

Model split up into three parts:

  1. sensor dynamics model \(\newcommand{\q}{\text{q}}\newcommand{\hs}{\hat{s}}\q(\hat{s}|\hat{e},\theta)\)
  2. environment dynamics model \(\newcommand{\q}{\text{q}}\newcommand{\ha}{\hat{a}}\q(\hat{e}'|\ha,\hat{e},\theta)\)
  3. initial environment distribution \(\newcommand{\q}{\text{q}}\newcommand{\hs}{\hat{s}}\q(\hat{e}|\theta)\)

1. Formal framework for a Bayesian agent

2. Generative model

Model split up into three parts:

  1. sensor dynamics model \(\newcommand{\q}{\text{q}}\newcommand{\hs}{\hat{s}}\q(\hat{s}|\hat{e},\theta)\)
  2. environment dynamics model \(\newcommand{\q}{\text{q}}\newcommand{\ha}{\hat{a}}\q(\hat{e}'|\ha,\hat{e},\theta)\)
  3. initial environment distribution \(\newcommand{\q}{\text{q}}\newcommand{\hs}{\hat{s}}\q(\hat{e}|\theta)\)

1. Formal framework for a Bayesian agent

3. Inference / prediction

As time passes in the perception action loop

  • new sensor values \(S_t=s_t\) and actions \(A_t=a_t\) are generated
  • get stored in \(M_t=m_t=sa_{\prec t}\)

 

As time passes in the perception action loop

  • new sensor values \(S_t=s_t\) and actions \(A_t=a_t\) are generated
  • get stored in \(M_t=m_t=sa_{\prec t}\)

 

1. Formal framework for a Bayesian agent

3. Inference / prediction

So at \(t\) agent can plug \(m_t=sa_{\prec t}\) into model

  • updates the probability distribution to a posterior:
\newcommand{\tT}{{t:T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{{q}} \newcommand{\hT}{{\hat{T}}} \newcommand{\diff}{\text{d}} \q(\hs_\thT,\he_{0:\hT},\ha_\thT,\theta|sa_\pt,\xi)

1. Formal framework for a Bayesian agent

3. Inference / prediction

So at \(t\) agent can plug \(m_t=sa_{\prec t}\) into model

  • updates the probability distribution to a posterior:
\newcommand{\tT}{{t:T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{{q}} \newcommand{\hT}{{\hat{T}}} \newcommand{\diff}{\text{d}} \q(\hs_\thT,\he_{0:\hT},\ha_\thT,\theta|sa_\pt,\xi)

1. Formal framework for a Bayesian agent

3. Inference / prediction

                                        predicts consequences of assumed actions \(\blue{\hat{a}_{t:\hat{T}}}\) for relations between:

\newcommand{\tT}{{t:T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\hT}{{\hat{T}}} \newcommand{\diff}{\text{d}} \q(\hs_\thT,\he_{0:\hT},\theta|\ha_\thT,sa_\pt,\xi)
  • parameters \(\red{\Theta}\)
  • latent variables \(\red{\hat{E}_{0:\hat{T}}}\)
  • future sensor values \(\red{\hat{S}_{t:\hat{T}}}\)

1. Formal framework for a Bayesian agent

3. Inference / prediction

Call \(\text{q}(\hat{s}_{t:\hat{T}},\hat{e}_{0:\hat{T}},\theta|\hat{a}_{t:\hat{T}},sa_{\prec t},\xi)\) the complete posteriors.  

  • This is the result of inference and a prediction at the same time

1. Formal framework for a Bayesian agent

3. Inference / prediction

1. Formal framework for a Bayesian agent

4. Action selection

  • define preferences / motivations as real valued functionals \(\mathfrak{M}\) of a complete posterior and a given sequence \(\hat{a}_{t:\hat{T}}\) of future actions:
\newcommand{\tT}{{t:T}}
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\mot}{\mathfrak{M}} \mot(\q(.,.,.|.,sa_\pt,\xi),\ha_\thT)
  • for a given complete posterior motivations imply optimal sequences:
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \ha^*_\thT(sa_\pt,\xi):=\argmax_{\ha_\thT} \mot(\q(.,.,.|.,sa_\pt,\xi),\ha_\thT)
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\re}{\text{r}} \text{q}(\ha_\thT|sa_\pt,\xi):=\frac{1}{Z} e^{\mot(\q(.,.,.|.,sa_\pt,\xi),\ha_\thT)}
  • and an according softmax policy:

1. Formal framework for a Bayesian agent

4. Action selection

Then either:

  • select the first action from the optimal sequence:
\newcommand{\tT}{{t:T}}
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\p}{\text{p}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \p(a_t|sa_\pt):=\delta_{\ha^*_t(sa_\pt,\xi)}(a_t)
  • or sample the first action from the softmax:
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\re}{\text{r}} \text{p}(a_t|sa_\pt):=\sum_{\ha_{t+1:\hT}} \frac{1}{Z} e^{\mot(\q(.,.,.|.,sa_\pt,\xi),\ha_\thT)}
  1. Formal framework for a Bayesian agent
    1. Perception-action loop
    2. Generative model
    3. Inference (obtaining a complete posterior)
    4. Action selection
  2. Active inference
  3. Some possible intrinsic motivations:
    1. Conditional entropy maximization
    2. Predictive information maximization
    3. Knowledge seeking
    4. Empowerment maximization
    5. Curiosity

Overview

2. Active inference

 

  • Formulates inference and action selection into a single optimization.
  • for this it introduces two main new objects
    • a variational complete posterior \(\text{r}(\hat{s}_{t:\hat{T}},\hat{e}_{0:\hat{T}},\theta|\hat{a}_{t:\hat{T}},\phi)\)
      which automatically has its associated softmax policy
      \(\text{q}(\hat{a}_{t:\hat{T}}|\phi)=e^{\mathfrak{M}(r(...|.,\phi),\hat{a}_{t:\hat{T}})}/Z\)
    • a variational policy \(\text{r}(\hat{a}_{t:\hat{T}}|\pi)\)
  • during optimization
    • the variational complete posterior approaches the true complete posterior (and so the associated softmax approaches the true softmax)
    • the variational policy approaches the associated softmax

2. Active inference

 

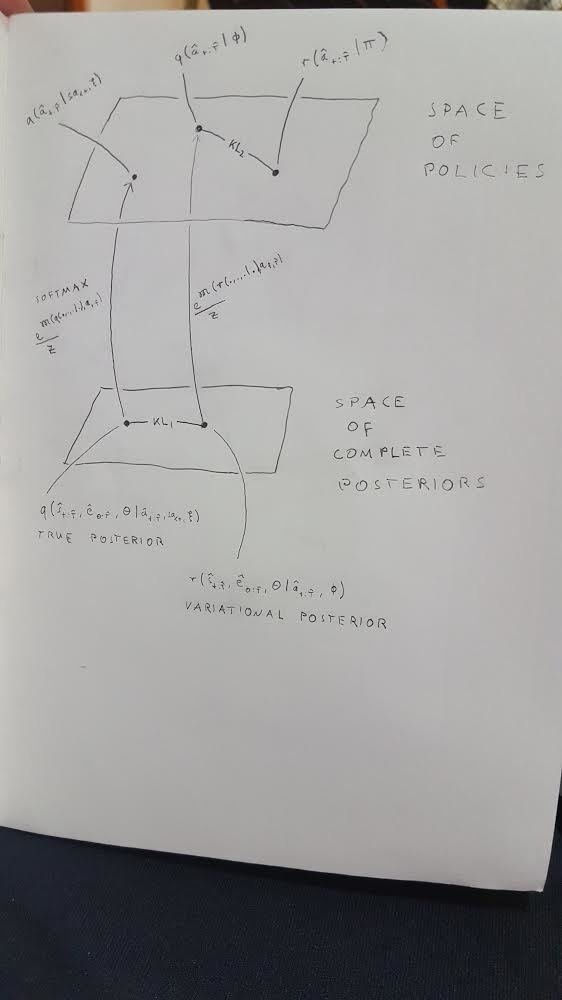
2. Active inference

 

\newcommand{\tT}{{t:T}} \newcommand{\tm}{{t-1}} \newcommand{\hT}{{\hat{T}}} \newcommand{\thT}{{t:\hT}} \newcommand{\allht}{{0:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\hS}{\hat{S}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\hE}{\hat{E}} \newcommand{\hA}{\hat{A}} \newcommand{\q}{\text{q}} \newcommand{\re}{\text{r}} \newcommand{\F}{\mathcal{F}} \newcommand{\diff}{\text{d}} \newcommand{\KL}{\text{KL}} \begin{aligned} \phi^*_{sa_\pt,\xi},\pi^*_{sa_\pt,\xi} : &=\text{argmin}_{\phi,\pi} \left(\sum_{\hs_\thT,\he_\allht,\theta,\ha_\thT}\re(\hs_\thT,\he_\allht,\theta,\ha_\thT|\pi,\phi) \log \frac{\re(\hs_\thT,\he_\allht,\theta,\ha_\thT|\pi,\phi)}{\q(s_\pt,\hs_\thT,\he_\allht,\theta,\ha_\thT|\phi,a_\pt,\xi)}\right) \\ &=\text{argmin}_{\phi,\pi} \left(\underbrace{\KL[\re(\hS_\thT,\hE_\allht,\Theta|\hA_\thT,\phi)||\q(\hS_\thT,\hE_\allht,\Theta|\hA_\thT,sa_\pt,\xi)]}_{\text{difference of complete posteriors}}+\underbrace{\KL[\re(\hA_\thT|\pi)||\q(\hA_\thT|\phi)]}_{\text{difference of policies}}\right) \end{aligned}

The free energy that active inference suggests to minimize is:

  • first term is inference, second is action selection
  • computational effort to minimize this is distributed to both terms
  • "precision" can be introduced to weight the two differently
  1. Formal framework for a Bayesian agent
    1. Perception-action loop
    2. Generative model
    3. Inference (obtaining a complete posterior)
    4. Action selection
  2. Active inference
  3. Some possible intrinsic motivations:
    1. Conditional entropy maximization
    2. Predictive information maximization
    3. Knowledge seeking
    4. Empowerment maximization
    5. Curiosity

Overview

  • We mentioned no restrictions on motivation functional \(\mathfrak{M}\) apart from real-valuedness.
  • both the standard Bayesian agent and the active inference approach work for any such functional
    • can choose the motivation freely!
  • very interesting types of motivations are intrinsic motivations (see e.g. Oudeyer (2008), Schmidhuber (2010))
  • expressions found in active inference literature often qualify as such intrinsic motivations

3. Some possible intrinsic motivations

Intrinsic motivations (roughly):

 

  • think of a motivation function that could drive a robot to learn about the world like human infants (developmental robotics)
  • work in any environment/embodiment (no special "reward sensor")
  • drive open-ended behavior (agents don't get stuck in dark rooms)

3. Some possible intrinsic motivations

In reinforcement learning (RL) the motivation is given by the expected sum over all values of one particular sensor, the "reward sensor" \(s^r\).

\newcommand{\tT}{{t:T}}
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\mot}{{\mathfrak{M}}} \begin{aligned} \mot(\q(.,.,.|.,sa_\pt,\xi),\ha_\thT):&= Q(\hat{a}_{t:\hat{T}},sa_{\prec t}) \\ :&= \sum_{\hs_\thT} \q(\hs^r_\thT|\ha_\thT,sa_\pt,\xi) \sum_{\tau=t}^{\hat{T}} \hs^r_\tau \end{aligned}

3. Some possible intrinsic motivations

0. Reinforcement learning

3. Some possible intrinsic motivations

1. Conditional entropy maximization

Actions should lead to environment states expected to have precise sensor values (e.g. Friston, Parr et al., 2017):

\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \q(\he_\thT|\ha_\thT)= \int \sum_{\hs_\thT,\he_\pt} \q(\hs_\thT,\he_{0:\hT},\theta|\ha_\thT) \diff \theta
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \begin{aligned} \mot(\q(.,.,.|.),\ha_\thT) :&=-\HS_{\q}(\hS_\thT|\hE_\thT,\ha_\thT)\\ &= \sum_{\he_\thT} \q(\he_\thT|\ha_\thT) \sum_{\hs_\thT} \q(\hs_\thT|\he_\thT) \log \q(\hs_\thT|\he_\thT)\\ \end{aligned}

Get \(\text{q}(\hat{e}_{t:\hat{T}}|\hat{a}_{t:\hat{T}})\) frome the complete posterior:

  • random noise sources are avoided
  • will get stuck in known "dark room traps"
    • we know $$\text{H}_{\text{q}}(\hat{S}_{t:\hat{T}}|\hat{a}_{t:\hat{T}})=0\Rightarrow\text{H}_{\text{q}}(\hat{S}_{t:\hat{T}}|\hat{E}_{t:\hat{T}},\hat{a}_{t:\hat{T}})=0$$
    • such an optimal action sequence \(\hat{a}_{t:\hat{T}}\) exists e.g. if there is a "dark room" in the environment
    • even if room cannot be escaped once entered and the agent knows it!

3. Some possible intrinsic motivations

1. Conditional entropy maximization

\newcommand{\hT}{{\hat{T}}} \newcommand{\thT}{{t:\hT}} \newcommand{\hTa}{{\hat{T}_a}} \newcommand{\thTa}{{t:\hTa}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\d}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\I}{\text{I}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \newcommand{\hA}{\hat{A}} \begin{aligned} \mot^{PI}(\d(.,.,.|.),\ha_\thT) :&= \I_{\q}(\hS_{t:t+k-1}:\hS_{t+k:t+2k-1}|\ha_\thT)\\ &=\sum_{\hs_{t:t+2k-1}} \q(\hs_{t:t+2k-1}|\ha_\thT) \log \frac{\q(\hs_{t+k:t+2k-1}|\hs_{t:t+k-1},\ha_\thT)}{\q(\hs_{t:t+k-1}|\ha_\thT)}\\ \end{aligned}

3. Some possible intrinsic motivations

2. Predictive information maximization

Actions should lead to the most complex sensor stream:

  • Next \(k\) sensor values should have max mutual information with the subsequent \(k\).
  • Proposed by Ay et. al (2008)

3. Some possible intrinsic motivations

2. Predictive information maximization

  • random noise source are avoided as they produce no mutual information
  • will not get stuck in known "dark room traps"
    • from $$\text{H}_{\text{q}}(\hat{S}_{t+k:t+2k-1}|\hat{a}_{t:\hat{T}})=0\Rightarrow\text{I}_{\text{q}}(\hat{S}_{t:t+k-1},\hat{S}_{t+k:t+2k-1}|\hat{a}_{t:\hat{T}})=0$$
  • possible long term behavior:
    • ergodic sensor process
    • finds a subset of environment states that allows this ergodicity

3. Some possible intrinsic motivations

2. Predictive information maximization

Georg Martius, Ralf Der

\newcommand{\hT}{{\hat{T}}} \newcommand{\thT}{{t:\hT}} \newcommand{\hTa}{{\hat{T}_a}} \newcommand{\thTa}{{t:\hTa}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\d}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\I}{\text{I}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \newcommand{\hA}{\hat{A}} \begin{aligned} \mot^{KSA}(\q(.,.,.|.),\ha_\thT) :&= \I_{\q}(\hS_\thT:\hE_{0:\hT},\Theta|\ha_\thT)\\ &=\sum_{\hs_\thT} \int \q(\hs_\thT,\he_{0:\hT},\theta|\ha_\thT) \log \frac{\q(\he_{0:\hT},\theta|\hs_\thT,\ha_\thT)}{\q(\theta)} \diff \theta \end{aligned}

3. Some possible intrinsic motivations

3. Knowledge seeking

Actions should lead to sensor values that tell the most about hidden (environment) variables \(\hat{E}_{0:\hat{T}}\) and model parameters \(\Theta\):

  • Also known as information gain maximization
  • Special cases occur in active inference literature (Friston, 2016) and in Orseau (2013)
  • Goes back at least to Lindley (1956) (thanks Thomas Parr!),

3. Some possible intrinsic motivations

3. Knowledge seeking

  • avoids random noise sources once they are known
  • will not get stuck in known "dark room traps"
    • from $$\text{H}_{\text{q}}(\hat{S}_{t:\hat{T}}|\hat{a}_{t:\hat{T}})=0\Rightarrow\text{I}_{\text{q}}(\hat{S}_{t:\hat{T}}:\hat{E}_{0:\hat{T}},\Theta|\hat{a}_{t:\hat{T}})=0$$
  • technical results exist by Orseau et al. (2013) (off-policy prediction!)
  • possible long term behavior:
    • when model is known does nothing / random walk

3. Some possible intrinsic motivations

3. Knowledge seeking

Bellemare et al. (2016)

Bellemare, M. G., Srinivasan, S., Ostrovski, G., Schaul, T., Saxton, D., and Munos, R. (2016). Unifying Count-Based Exploration and Intrinsic Motivation. arXiv:1606.01868 [cs]. arXiv: 1606.01868.

 

\newcommand{\hT}{{\hat{T}}} \newcommand{\thT}{{t:\hT}} \newcommand{\hTa}{{\hat{T}_a}} \newcommand{\thTa}{{t:\hTa}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\d}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\I}{\text{I}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \newcommand{\hA}{\hat{A}} \begin{aligned} \mot^{EM}(\d(.,.,.|.),\ha_\thTa) :&= \max_{\d(\ha_{\hTa+1:\hT})} \; \I_{\d}(\hA_{\hTa+1:\hT}:\hS_\hT|\ha_\thTa) \\ &=\max_{\d(\ha_{\hTa+1:\hT})} \; \sum_{\ha_{\hTa+1:\hT},\hs_\hT} \d(\ha_{\hTa+1:\hT}) \d(\hs_\hT|\ha_\thT) \log \frac{\d(\hs_\hT|\ha_\thT)}{\d(\hs_\hT|\ha_\thTa)}. \end{aligned}

3. Some possible intrinsic motivations

4. Empowerment maximization

Actions should lead to control over as many future experiences as possible:

  • Actions \(\hat{a}_{t:\hat{T}_a}\) are taken such that subsequent actions \(\hat{a}_{\hat{T}_a+1:\hat{T}}\) have control
  • proposed by Klyubin and Polani (2005)

3. Some possible intrinsic motivations

4. Empowerment maximization

  • avoids random noise sources because they cannot be controlled
  • will not get stuck in known "dark room traps"
    • from $$\text{H}_{\text{q}}(\hat{S}_{\hat{T}}|\hat{a}_{t:\hat{T}_a})=0\Rightarrow\text{I}_{\text{q}}(\hat{A}_{\hat{T}_a+1:\hat{T}}\hat{S}_{\hat{T}}:|\hat{a}_{t:\hat{T}_a})=0$$
  • similar to energy and money maximization but more general
  • possible long term behavior:
    • remains in (or maintains) the situation where it expects the most control over future experience
    • exploration behavior not fully understood
    • Belief empowerment may solve it...

3. Some possible intrinsic motivations

4. Empowerment

Guckelsberger et al. (2016)

Guckelsberger, C., Salge, C., & Colton, S. (2016). Intrinsically Motivated General Companion NPCs via Coupled Empowerment Maximisation. 2016 IEEE Conf. Computational Intelligence in Games (CIG’16), 150–157

3. Some possible intrinsic motivations

5a. Curiosity

Actions should lead to surprising sensor values.

\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \begin{aligned} \mot(\q(.,.,.|.),\ha_\thT) :&=+\HS_{\q}(\hS_\thT|\ha_\thT)\\ &= \sum_{\hs_\thT} \q(\hs_\thT|\ha_\thT)(- \log \q(\hs_\thT|\ha_\thT))\\ \end{aligned}
  • Also called Shannon knowledge seeking (Orseau)
  • maximize expected surprise (=entropy)
  • Get density from the complete posterior.

3. Some possible intrinsic motivations

5a. Curiosity

  • will not get stuck in known "dark room traps"
    • it directly pursues the opposite situation
  • will get stuck at random noise sources
  • in deterministic environments not a problem
    • proven to asymptotically drive an agent to the behavior of an agent that knows the environment (under some technical conditions, see Orseau, 2011)

3. Some possible intrinsic motivations

5b. Curiosity

Actions should lead to surprising environment states.

  • I have never seen this explicitly
  • Get density from the complete posterior.
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \begin{aligned} \mot(\q(.,.,.|.),\ha_\thT) :&=+\HS_{\q}(\hE_\thT|\ha_\thT)\\ &= \sum_{\hs_\thT} \q(\he_\thT|\ha_\thT)(- \log \q(\he_\thT|\ha_\thT))\\ \end{aligned}

3. Some possible intrinsic motivations

5b. Curiosity

Actions should lead to surprising embedding of sensor values:

  • Something between the last two
  • Get density from the complete posterior.
\newcommand{\hT}{\hat{T}} \newcommand{\thT}{{t:\hT}} \newcommand{\hs}{\hat{s}} \newcommand{\pt}{{\prec t}} \newcommand{\pet}{{\preceq t}} \newcommand{\set}{{\succeq t}} \newcommand{\ha}{\hat{a}} \newcommand{\he}{\hat{e}} \newcommand{\q}{\text{q}} \newcommand{\diff}{\text{d}} \newcommand{\ptau}{{\prec \tau}} \newcommand{\petau}{{\preceq \tau}} \newcommand{\stau}{{\succ \tau}} \newcommand{\setau}{{\succeq \tau}} \newcommand{\argmax}{\text{argmax}} \newcommand{\mot}{\mathfrak{M}} \newcommand{\HS}{\text{H}} \newcommand{\hS}{\hat{S}} \newcommand{\hE}{\hat{E}} \begin{aligned} \mot(\q(.,.,.|.,\xi),\ha_\thT) :&=+\HS_{\q}(f(\hS_\thT)|\ha_\thT)\\ &= \sum_{\hs_\thT} \q(f(\hs_\thT)|\ha_\thT)(- \log \q(f(\hs_\thT)|\ha_\thT))\\ \end{aligned}

3. Some possible intrinsic motivations

5. Curiosity

Burda et al. (2018) with permission.

Burda, Y., Edwards, H., Pathak, D., Storkey, A., Darrell, T., and Efros, A. A. (2018). Large-Scale Study of Curiosity-Driven Learning.  arXiv:1808.04355 [cs, stat]. arXiv: 1808.04355.

  • active inference converges to standard Bayesian agent (and RL if motivation function is cumulative reward, ignoring the open vs closed loop issue)
  • active inference does not imply a particular motivation function (but maybe in the Markov blanket approach it does?)
  • mutiple intrinsic motivations solve dark room problem without external reward

Conclusions

Ay, N., Bertschinger, N., Der, R., Güttler, F., and Olbrich, E. (2008). Predictive Information and Explorative Behavior of Autonomous Robots. The European Physical Journal B-Condensed Matter and Complex Systems, 63(3):329–339.

 

Biehl, M., Guckelsberger, C., Salge, C., Smith, S. C., and Polani, D. (2018). Expanding the Active Inference Landscape: More Intrinsic Motivations in the Perception-Action Loop. Frontiers in Neurorobotics, 12.

 

Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., O’Doherty, J., and Pezzulo, G. (2016). Active Inference and Learning. Neuroscience & Biobehavioral Reviews, 68(Supplement C):862–879.


Friston, K. J., Parr, T., and de Vries, B. (2017). The Graphical Brain: Belief Propagation and Active Inference. Network Neuroscience, 1(4):381–414.


Klyubin, A., Polani, D., and Nehaniv, C. (2005). Empowerment: A Universal Agent-Centric Measure of Control. In The 2005 IEEE Congress on Evolutionary Computation, 2005, volume 1, pages 128–135.


Orseau, L., Lattimore, T., and Hutter, M. (2013). Universal Knowledge-Seeking Agents for Stochastic Environments. In Jain, S., Munos, R., Stephan, F., and Zeugmann, T., editors, Algorithmic Learning Theory, number 8139 in Lecture Notes in Computer Science, pages 158–172. Springer Berlin Heidelberg.

 

Oudeyer, P.-Y. and Kaplan, F. (2008). How can we define intrinsic motivation? In Proceedings of the 8th International Conference on Epigenetic Robotics: Modeling Cognitive Development in Robotic Systems, Lund University Cognitive Studies, Lund: LUCS, Brighton. Lund University Cognitive Studies, Lund: LUCS, Brighton.


Schmidhuber, J. (2010). Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3):230–247.

 

Guckelsberger, C., Salge, C., & Colton, S. (2016). Intrinsically Motivated General Companion NPCs via Coupled Empowerment Maximisation. 2016 IEEE Conf. Computational Intelligence in Games (CIG’16), 150–157

 

Lindley, D. V. (1956). On a Measure of the Information Provided by an Experiment. The Annals of Mathematical Statistics, 27(4):986–1005.

 

 

 

Copy of The intrinsic motivation in active inference and possible alternatives

By slides_martin

Made with Slides.com

Copy of The intrinsic motivation in active inference and possible alternatives

Actual slides I used for the presentation at CCS 2018 workshop: http://ccs2018.web.auth.gr/fromCellsToConsciousness

  • 698

More from slides_martin