\text{Chapter 19}

\text{Review}

\text{Dr. Adel Abbout}

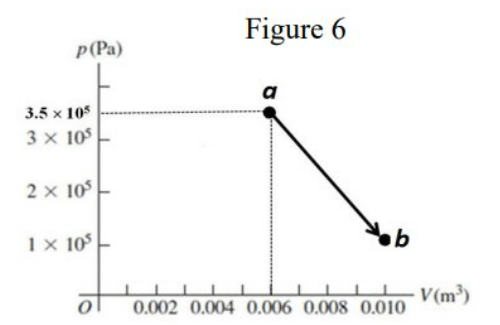
\text{One mole of an ideal monatomic gas is taken along the path $a b$ shown as the solid line in FIGURE 6.}

\text{Find the amount of heat that is transferred into or out of the gas along the path $a b$.}

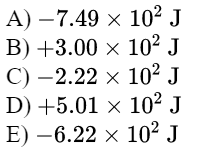
\text{One mole of an ideal monatomic gas is taken along the path $a b$ shown as the solid line in FIGURE 6.}

\text{Find the amount of heat that is transferred into or out of the gas along the path $a b$.}

\begin{aligned} & \Delta E_{a b}=Q_{a b}-W_{a b} \\ & Q_{a b}=\Delta E_{ a b}+W_{a b} \\ & \Delta E_{a b}=n C_v\left(T_b-T_a\right)=n \cdot \frac{3}{2} R\left(\frac{P_b V_b}{n R}-\frac{P_a V_a}{n R}\right) \\ & =\frac{3}{2}\left(P_b V_b-P_a V_a\right)=\frac{3}{2}\left(10^5 \times 0.01-3.5 \times 10^5 \times 0.006\right) \\ & \Delta E_{a b}=-1650 \mathrm{~J} \\ & W_{a b}=10^5 \times(0.01-0.006)+\frac{(0.01-0.006) \times 2.5 \times 10^5}{2}=400+500=900 \mathrm{~J} \\ & Q_{a b}=-1650+900=-750 \mathrm{~J} \\ & \end{aligned}

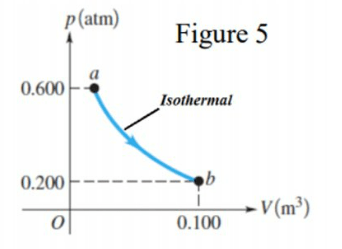
\text{In the isothermal process $\boldsymbol{a} \rightarrow \boldsymbol{b}$ shown in Figure 5, the temperature of an ideal gas remains constant}

\text{at $85.0^{\circ} \mathrm{C}$. Find the magnitude of the work done by the gas during the process $a \rightarrow b$.}

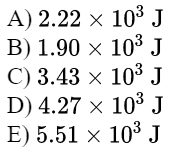
\text{In the isothermal process $\boldsymbol{a} \rightarrow \boldsymbol{b}$ shown in Figure 5, the temperature of an ideal gas remains constant}

\text{at $85.0^{\circ} \mathrm{C}$. Find the magnitude of the work done by the gas during the process $a \rightarrow b$.}

\begin{aligned} & W=n R T \ln \left(\frac{V_f}{V_i}\right)=P_b V_b \ln \left(\frac{P_a}{P_b}\right) \\ & =0.2 \times 1.01 \times 10^5 \times 0.1 \times \ln \left(\frac{0.6}{0.2}\right)=2219.2 \mathrm{~J} \end{aligned}

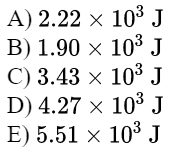
PV=nRT

P_aV_a=P_bV_b

(T=\text{const})

\text{we can keep "atm"}

\text{we need to change "atm" to "Pa"}

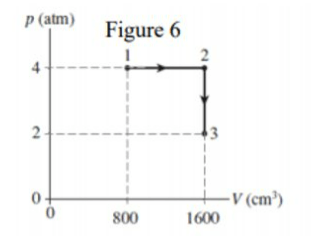
\text{A monatomic ideal gas with 0.10 mol follow the processes $1 \rightarrow 2$ and $2 \rightarrow 3$, as shown in Figure 6.}

\text{Determine the net heat exchanged during these processes $(1 \rightarrow 2$ and 2 $\rightarrow 3$ ).}

\text{A monatomic ideal gas with 0.10 mol follow the processes $1 \rightarrow 2$ and $2 \rightarrow 3$, as shown in Figure 6.}

\text{Determine the net heat exchanged during these processes $(1 \rightarrow 2$ and 2 $\rightarrow 3$ ).}

\begin{aligned} \Delta Q_P & =n C_p \Delta T_{12}=\frac{C_p}{R} P \Delta V=\frac{5}{2} P \Delta V \\ & =\frac{5}{2} \times 4 \times 1.01 \times 10^5 \times 800 \times 10^{-6}=808 \mathrm{~J} \end{aligned}

PV=nRT

C_V=\frac{3}{2}R

C_p=\frac{5}{2}R

\text{monoatomic gas}

T_3-T_2=(P_3V_3-P_2V_2)/nR=V(P_3-P_2)/nR

\text{because } V_3=V_2

T_2-T_1=(P_2V_2-P_1V_1)/nR=P(V_2-V_1)/nR

\text{because } P_2=P_1

\begin{aligned} \Delta Q_V & =n C_V \Delta T_{23}=\frac{C_V}{R} V \Delta P=\frac{3}{2} V \Delta P \\ & =\frac{3}{2} \times 1600 \times 10^{-6} \times\left(-2 \times 1.04 \times 10^5\right)=-484.84 \mathrm{~J} \\ \Delta Q_{\text {net }} & =\Delta Q_P+\Delta Q_V=808-484.8=323.2 \mathrm{~J} \end{aligned}

\text{Problem: (Chapter 19)}

\text{Problem: (Chapter 19)}

\text{1) Ice at }-10^0C\text{ to ice at }0^0C

Q=mc_{ice}\Delta T= 10^{-2} \times2220 \times 10=222 J

\displaystyle \Delta S=m c_{ice}\ln\Big(\frac{T_\text{f}}{T_i}\Big)=10^{-2} \times 2220\times \ln\Big(\frac{273}{263}\Big)=0.828 J/K

\text{Problem: (Chapter 19)}

\text{1) Ice at }-10^0C\text{ to ice at }0^0C

Q=mc_{ice}\Delta T= 10^{-2} \times2220 \times 10=222 J

\displaystyle \Delta S=m c_{ice}\ln\Big(\frac{T_\text{f}}{T_i}\Big)=10^{-2} \times 2220\times \ln\Big(\frac{273}{263}\Big)=0.828 J/K

\text{2) Melting ice }

Q=mL_{F}=10^{-2}=10^{-2}\times 333\times 10^3=3330 J

\displaystyle \Delta S=mL_{F}/T=Q/T=3330/273=12.20 J/K

\text{Problem: (Chapter 19)}

\text{1) Ice at }-10^0C\text{ to ice at }0^0C

Q=mc_{ice}\Delta T= 10^{-2} \times2220 \times 10=222 J

\displaystyle \Delta S=m c_{ice}\ln\Big(\frac{T_\text{f}}{T_i}\Big)=10^{-2} \times 2220\times \ln\Big(\frac{273}{263}\Big)=0.828 J/K

\text{2) Melting ice }

Q=mL_{F}=10^{-2}=10^{-2}\times 333\times 10^3=3330 J

\displaystyle \Delta S=mL_{F}/T=Q/T=3330/273=12.20 J/K

\text{3) Water at }0^0\text{ to water at }15^0C

Q=mc_{w}\Delta T= 10^{-2} \times4190 \times 15=629 J

\displaystyle \Delta S=m c_{w}\ln\Big(\frac{T_\text{f}}{T_i}\Big)=10^{-2} \times 4190\times \ln\Big(\frac{288}{273}\Big)=2.24 J/K

\text{Problem: (Chapter 19)}

Q_{ice}=Q_1+Q_2+Q_3=222+3330+629=4181 J

\Delta S_{ice}=\Delta S_1+\Delta S_2+\Delta S_3=0.828+12.20+2.24=15.27\frac{J}{K}

Q_{lake}=-Q_{ice}=-4181J

\text{The temperature of the lake doesnt change, so, the }\\ \text{change in the entropy is:}

\Delta S_{lake}=\frac{Q}{T}=-\frac{4181}{288}=-14.51 \frac{J}{K}

\Delta S_{total}=\Delta S_{ice}+\Delta S_{lake}=15.27-14.51=0.76 J/K

\Delta S_{total}>0 \text{ as required by the second law of thermodynamics}

\text{Lake system:}