\text{Chapter 23}
\text{Chapter 23}
\text{Chapter 23}
\text{Chapter 23}
\text{Non-conducting}
\sigma
E=\frac{\sigma}{2\epsilon_0}
E=-\frac{\sigma}{2\epsilon_0}
\text{right side}
\text{left side}
\text{valid for any sign of $\sigma$}
E=\frac{\lambda}{2\pi \epsilon_0 r}
E=-\frac{\lambda}{2\pi \epsilon_0 r}
\lambda
\text{right side}
\text{left side}
\text{valid for any sign of $\lambda$}
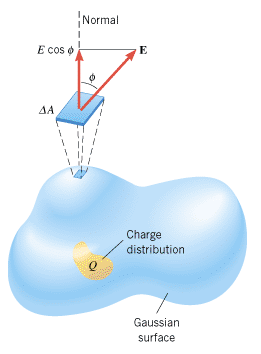
\epsilon_0\phi=q_\text{enc}
\text{(charges inside volume only)}
\text{Rod}
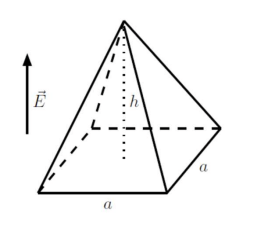
\text{The figure shows a pyramid with horizontal square base, $a=6.00 \mathrm{~m}$ on each side, and a height,}
\text{$h=$ $4.00 \mathrm{~m}$. The pyramid is placed in an upward vertical electric field of magnitude $E=52.0 \mathrm{~N} / \mathrm{C}$.}
\text{If the pyramid does not include any charge inside, calculate the electric flux, in $\mathrm{N} . \mathrm{m}^2 / \mathrm{C}$, through }
\text{its four slanted (inclined) surfaces.}
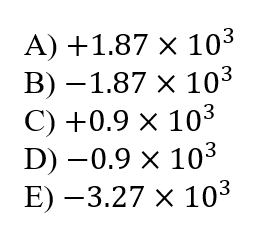
\text{The figure shows a pyramid with horizontal square base, $a=6.00 \mathrm{~m}$ on each side, and a height,}
\text{$h=$ $4.00 \mathrm{~m}$. The pyramid is placed in an upward vertical electric field of magnitude $E=52.0 \mathrm{~N} / \mathrm{C}$.}
\text{If the pyramid does not include any charge inside, calculate the electric flux, in $\mathrm{N} . \mathrm{m}^2 / \mathrm{C}$, through }
\text{its four slanted (inclined) surfaces.}

\text { Gauss' Law: } \varepsilon_0 \phi=q_{\text {enc }}
\text { Since } q_{e n c}=0 \Rightarrow \phi=0
\phi_{\text {base }}+\phi_{\text {sides }}=0
\phi_{\text {base }}=\vec{E} \cdot \vec{A}=E A \cos 180=-E a^2
\text{(because no charge inside)}
\vec{A}
\phi_{\text {sides }}=-\phi_{\text {base }}=E a^2=52\times6^2 \frac{N m^2}{\mathrm{C}}
\phi_{\text {sides }}=1.87 \times 10^3 \frac{\mathrm{Nm^2}}{\mathrm{c}}
\text{(vector area is out of the volume)}
\text{Answer A}
\text{Two very large, non-conducting plastic sheets, each $10 \mathrm{~cm}$ thick, carry uniform surface charge}
\text{densities $\sigma_1, \sigma_2, \sigma_3$, and $\sigma_4$ on their surfaces, as shown in Figure 4 . These surface charge densities}
\text{have values $\sigma_1=-3.5 \mu \mathrm{C} / \mathrm{m}^2, \sigma_2=+3.0 \mu \mathrm{C} / \mathrm{m}^2, \sigma_3=+1.5 \mu \mathrm{C} / \mathrm{m}^2$, and $\sigma_4=-2.5 \mu \mathrm{C} / \mathrm{m}^2$.}
\text{Find the magnitude of the ratio $\left(E_A / E_B\right)$ of the electric field $E_A$ at the points $A$ to that $E_B$ at }
\text{the point B far from the edges of these sheets:}
A
B
\cdot
\cdot
\sigma_1
\sigma_3
\sigma_2
\sigma_4

10\text{ cm}
10\text{ cm}
12\text{ cm}
\text{Two very large, non-conducting plastic sheets, each $10 \mathrm{~cm}$ thick, carry uniform surface charge}
\text{densities $\sigma_1, \sigma_2, \sigma_3$, and $\sigma_4$ on their surfaces, as shown in Figure 4 . These surface charge densities}
\text{have values $\sigma_1=-3.5 \mu \mathrm{C} / \mathrm{m}^2, \sigma_2=+3.0 \mu \mathrm{C} / \mathrm{m}^2, \sigma_3=+1.5 \mu \mathrm{C} / \mathrm{m}^2$, and $\sigma_4=-2.5 \mu \mathrm{C} / \mathrm{m}^2$.}
\text{Find the magnitude of the ratio $\left(E_A / E_B\right)$ of the electric field $E_A$ at the points $A$ to that $E_B$ at }
\text{the point B far from the edges of these sheets:}
A
B
\cdot
\cdot
\sigma_1
\sigma_3
\sigma_2
\sigma_4
10\text{ cm}
10\text{ cm}
12\text{ cm}
\begin{aligned}
E_A & =\frac{1}{2 \varepsilon_0}\left[-\left|\sigma_1\right|-\left|\sigma_2\right|-\left|\sigma_3\right|+\left|\sigma_4\right|\right] \\
& =\frac{1}{2 \varepsilon_0}[-3.5-3.0-1.5+2.5] \times 10^{-6}=-\frac{5.5 \times 10^{-6}}{2 \varepsilon_0} \text{N/C}\\
E_B & =\frac{1}{2 \varepsilon_0}\left[-\left|\sigma_1\right|+\left|\sigma_2\right|+\left|\sigma_3\right|+\left|\sigma_4\right|\right] \\
& =\frac{1}{2 \varepsilon_0}[-3.5+3.0+1.5+2.5] \times 10^{-6}=+\frac{3.5 \times 10^{-6}}{2 \varepsilon_0} \text{N/C}\\
\frac{\left|E_A\right|}{\left|E_B\right|} & =\frac{5.5}{3.5}=1.57
\end{aligned}
\text{Figure 4 shows, in cross section, two solid insulating spheres with uniformly distributed charge}
\text{throughout their volumes. Each sphere has radius $\mathrm{R}=0.600 \mathrm{~m}$. Point $P$ lies on a line connecting }
\text{the centers of the spheres, at radial distance $R / 2$ from the center of sphere 1 which carries }
\text{a charge $\mathrm{q}_1=40.0 \mu \mathrm{C}$. If the net electric field at point $P$ is zero, what is the charge $\mathrm{q}_2$ on the sphere $2 ?$}
\cdot
\cdot
R
R
\cdot
1
2
P
\text{Figure 4 shows, in cross section, two solid insulating spheres with uniformly distributed charge}
\text{throughout their volumes. Each sphere has radius $\mathrm{R}=0.600 \mathrm{~m}$. Point $P$ lies on a line connecting }
\text{the centers of the spheres, at radial distance $R / 2$ from the center of sphere 1 which carries }
\text{a charge $\mathrm{q}_1=40.0 \mu \mathrm{C}$. If the net electric field at point $P$ is zero, what is the charge $\mathrm{q}_2$ on the sphere $2 ?$}
\cdot
\cdot
R
R
\cdot
1
2
\left|E_1\right|=\left|E_2\right|
\begin{aligned}
& \frac{k q_1}{R^3} \times \frac{R}{2}= \frac{k q_2}{\displaystyle\left(\frac{3 R}{2}\right)^2} \\
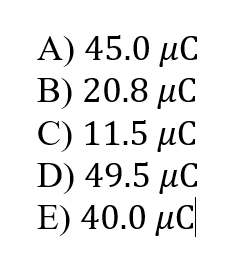
& \frac{q_1}{2 {R}^2}=\frac{4 q_2}{9 {R}^2} \Rightarrow q_2=\frac{9}{8} q_1=\frac{9}{8} \times 40 \times 10^{-6}=45 \times 10^{-6} \mathrm{C}
\end{aligned}
\text{We use superposition theorem}
\vec{E}=\vec{E}_1+\vec{E}_2=0
\text{At P,}
\text{reminder:}
\text{inside a charged sphere}
\text{outside a charged sphere}
E=k\frac{q}{R^3}r
E=k\frac{q}{r^2}
P
\frac{R}{2}
\frac{3R}{2}
\text{Consider two infinitely long thin wires carrying uniform linear charge densities $\lambda_1$ and $\lambda_2$.}
\text{The wires are arranged as shown in the figure and $\lambda_2=+5.50\hspace{1 mm} \mathrm{ nC} / \mathrm{m}$. If the net electric field}
\text{at $P$ is zero, determine the magnitude of $\lambda_1$.}

\cdot
2\text{ cm}
2\text{ cm}
\lambda_1
\lambda_2
P
\text{Consider two infinitely long thin wires carrying uniform linear charge densities $\lambda_1$ and $\lambda_2$.}
\text{The wires are arranged as shown in the figure and $\lambda_2=+5.50\hspace{1 mm} \mathrm{ nC} / \mathrm{m}$. If the net electric field}
\text{at $P$ is zero, determine the magnitude of $\lambda_1$.}

\text{Superposition principle}
\vec{E}=\vec{E}_1+\vec{E}_2
\text{At point P,}
\vec{E}=0
\Rightarrow
E_1=E_2
\text{(magnitudes)}
\Rightarrow
\frac{|\lambda_1|}{2\pi\epsilon_0 r_1}=\frac{|\lambda_2|}{2\pi\epsilon_0 r_2}
\Rightarrow
{|\lambda_1|}=\frac{r_1}{ r_2} |\lambda_1|
\Rightarrow
{|\lambda_1|}=\frac{2 \text{ cm}}{ 4 \text{ cm}} 5.5 \text{ n.C/m}=2.75 \text{ n.C/m}
\cdot
2\text{ cm}
2\text{ cm}
\lambda_1
\lambda_2
P
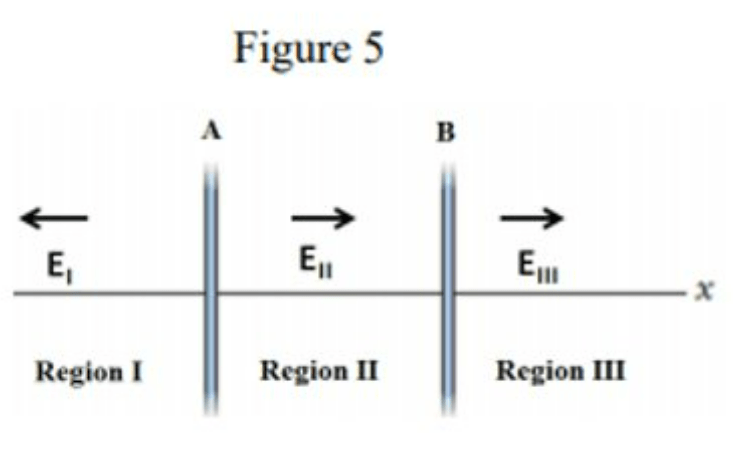
\text{Two vertical insulating charged planes A and B with negligible thickness are parallel. }
\text{The magnitude of the electric field $\overrightarrow{\mathrm{E}}_1$ in region I is $\frac{3 \sigma}{2 \varepsilon_{\mathrm{o}}}$ while the magnitude of electric field $\overrightarrow{\mathrm{E}}_{\mathrm{III}}$ }
\text{in the region III is $\frac{3 \sigma}{2 \varepsilon_{\mathrm{o}}}$, where $\sigma$ is a positive surface charge density. The magnitude of electric }
\text{field $\overrightarrow{\mathrm{E}}_{\mathrm{II}}$ in the region II is $\frac{\sigma}{2 \varepsilon_{\mathrm{o}}}$, Figure 5 shows the directions of the electric field in each of the regions.}
\text{Determine the surface charge density on planes A and B, respectively.}
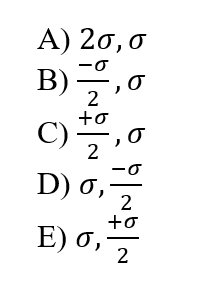
\text{Two vertical insulating charged planes A and B with negligible thickness are parallel. }
\text{The magnitude of the electric field $\overrightarrow{\mathrm{E}}_1$ in region I is $\frac{3 \sigma}{2 \varepsilon_{\mathrm{o}}}$ while the magnitude of electric field $\overrightarrow{\mathrm{E}}_{\mathrm{III}}$ }
\text{in the region III is $\frac{3 \sigma}{2 \varepsilon_{\mathrm{o}}}$, where $\sigma$ is a positive surface charge density. The magnitude of electric }
\text{field $\overrightarrow{\mathrm{E}}_{\mathrm{II}}$ in the region II is $\frac{\sigma}{2 \varepsilon_{\mathrm{o}}}$, Figure 5 shows the directions of the electric field in each of the regions.}
\text{Determine the surface charge density on planes A and B, respectively.}

\begin{aligned}
& \frac{\sigma_A}{2 \epsilon_0}-\frac{\sigma_B}{2 \epsilon_0}=\frac{\sigma}{2 \epsilon_0} \\
& \sigma_A-\sigma_B=\sigma \rightarrow(1)
\end{aligned}
\\
\begin{aligned}
& \frac{\sigma_A}{2 \epsilon_0}+\frac{\sigma_B}{2 \epsilon_0}=\frac{3 \sigma}{2 \epsilon_0} \\
& \sigma_A+\sigma_B=3 \sigma \rightarrow(2)
\end{aligned}
\\
\begin{aligned}
\sigma_A & =2 \sigma \\
\sigma_B & =\sigma
\end{aligned}
\text{In the region II}\\
\text{In the region III}
\text{From (1) and (2) we have}
\text{A $6.0 \mu \mathrm{C}$ charge is placed on a thin spherical conducting shell of radius $\mathrm{R}=5.0 \mathrm{~cm}$. A particle}
\text{with a charge of $-10 \mu \mathrm{C}$ is placed at the center of the shell. The magnitude and direction of the }
\text{electric field at a point 2R from the center of the shell are:}

\text{A $6.0 \mu \mathrm{C}$ charge is placed on a thin spherical conducting shell of radius $\mathrm{R}=5.0 \mathrm{~cm}$. A particle}
\text{with a charge of $-10 \mu \mathrm{C}$ is placed at the center of the shell. The magnitude and direction of the }
\text{electric field at a point 2R from the center of the shell are:}

\mathrm{E}=\frac{k(6.0 \mu C-10 \mu C)}{(2 R)^2}=3.6 \times 10^6 \mathrm{~N} / \mathrm{C}
\text{Superposition principle}
\text{A long, straight wire has fixed negative charge with a linear charge density of magnitude }
\text{$4.5 \mathrm{nC} / \mathrm{m}$. The wire is enclosed by a coaxial, thin walled nonconducting cylindrical shell }
\text{of radius 20 cm . The shell is to have a positive charge on its outside surface }
\text{(with a surface charge density $\sigma$ ) that makes the net electric field at points 30 cm from }
\text{the center of the shell equal to zero. Calculate $\sigma$.}
\text{A) $3.6 \times 10^{-9} \mathrm{C} / \mathrm{m}^2$}
\text{B) $3.0 \times 10^{-10} \mathrm{C} / \mathrm{m}^2$}
\text{C) $1.5 \times 10^{-10} \mathrm{C} / \mathrm{m}^2$}
\text{D) $4.5 \times 10^{-7} \mathrm{C} / \mathrm{m}^2$}
\text{E) $7.8 \times 10^{-5} \mathrm{C} / \mathrm{m}^2$}
\begin{aligned}
& \mathrm{E}=\frac{\lambda_1}{2 \pi \epsilon_0 r}+\frac{\lambda_2}{2 \pi \epsilon_0 r}=0 \\
& \lambda_1=\lambda_2=\frac{\mathrm{q}}{l}=\frac{\sigma \mathrm{A}}{l}=\frac{\sigma 2 \pi \mathrm{R} l}{l} \\
& \Rightarrow \sigma=\frac{\lambda_1}{2 \pi \mathrm{R}}=\frac{4.5 \times 10^{-9}}{2 \pi(0.2)} \\
& =3.6 \times 10^{-9} \mathrm{C}
\end{aligned}
\text{A long, straight wire has fixed negative charge with a linear charge density of magnitude }
\text{$4.5 \mathrm{nC} / \mathrm{m}$. The wire is enclosed by a coaxial, thin walled nonconducting cylindrical shell }
\text{of radius 20 cm . The shell is to have a positive charge on its outside surface }
\text{(with a surface charge density $\sigma$ ) that makes the net electric field at points 30 cm from }
\text{the center of the shell equal to zero. Calculate $\sigma$.}
\text{A point charge is placed at the center of an imaginary cube that has 20\ cm-long edges.}
\text{The electric flux out of one of the cube's sides is $-2.5 $ $ kN.m^2/C$.}
\text{How much charge is at the center?}
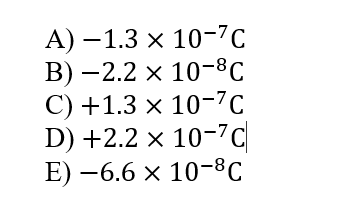
\begin{aligned}
& \text{A) $\Phi_{\mathrm{a}}, \Phi_{\mathrm{b}}$, and $\Phi_{\mathrm{c}}$ tie, $\Phi_{\mathrm{d}}$}\\
& \text{B) $\Phi_{\mathrm{d}}, \Phi_{\mathrm{a}}, \Phi_{\mathrm{b}}, \Phi_{\mathrm{c}}$}\\
& \text{C) $\Phi_{\mathrm{d}}$ than $\Phi_{\mathrm{a}}, \Phi_{\mathrm{b}}$, and $\Phi_{\mathrm{c}}$ tie}\\
& \text{D) $\Phi_{\mathrm{d}}, \Phi_{\mathrm{b}}, \Phi_{\mathrm{c}}, \Phi_{\mathrm{a}}$}\\
& \text{E) $\Phi_{\mathrm{d}}$ and $\Phi_{\mathrm{b}}$ tie, $\Phi_{\mathrm{a}}$ and $\Phi_{\mathrm{c}}$ tie}\\
\end{aligned}
\begin{aligned}
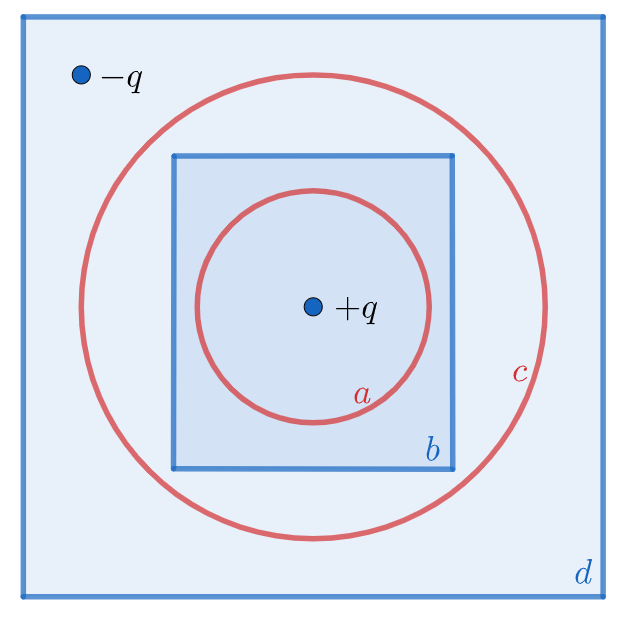
&\text{FIGURE 5 shows, in cross section, two Gaussian spheres and two Gaussian cubes. A positive }\\
&\text{charge +q is placed at the center of inner sphere "a" and a charge of -q is placed between the} \\
&\text{sphere "c" and the cube "d". Rank the net flux $\Phi$ through the four Gaussian }\\
&\text{surfaces, GREATEST FIRST.}
\end{aligned}

\begin{aligned}
&\text{FIGURE 5 shows, in cross section, two Gaussian spheres and two Gaussian cubes. A positive }\\
&\text{charge +q is placed at the center of inner sphere "a" and a charge of -q is placed between the} \\
&\text{sphere "c" and the cube "d". Rank the net flux $\Phi$ through the four Gaussian }\\
&\text{surfaces, GREATEST FIRST.}
\end{aligned}
\text{Gauss law states:}
\epsilon_0\phi=q_\text{enc}
\Phi_a=\Phi_b=\Phi_c=\frac{+q}{\epsilon_0}
\text{We deduce that}
\Phi_d=\frac{+q-q}{\epsilon_0}=0
\text{Answer A}
Chapter 23
By smstry
Chapter 23
- 625



