\text{Chapter 24}
\text{Chapter 24}
\text{Chapter 24}
\text{Chapter 24}
\text{An electron is released from rest at the origin in a uniform electric field that points in the }
\text{positive $x$ direction and has a magnitude of $850 \mathrm{~N} / \mathrm{C}$. What is the change in the electric }
\text{potential energy of the electron-field system when the electron moves a distance of $2.5 \mathrm{~m}$ ?}
\text{B) $+3.4 \times 10^{-16} \mathrm{~J}$}
\text{A) $-3.4 \times 10^{-16} \mathrm{~J}$}
\text{C) $-1.4 \times 10^{-16} \mathrm{~J}$}
\text{D) $+1.4 \times 10^{-16} \mathrm{~J}$}
\text{E) $-5.4 \times 10^{-16} \mathrm{~J}$}
\text{An electron is released from rest at the origin in a uniform electric field that points in the }
\text{positive $x$ direction and has a magnitude of $850 \mathrm{~N} / \mathrm{C}$. What is the change in the electric }
\text{potential energy of the electron-field system when the electron moves a distance of $2.5 \mathrm{~m}$ ?}
\Delta U=-W_{\text {field }}=-\int_{i}^f \vec{F} \cdot d \vec{s}=-\int_i^f q \vec{E} \cdot d \vec{s}
\Delta U=-W_{\text {field }}=-\int_i^f (-e) {E} \cdot d{s}\cdot \cos 180^0=-\int_i^f e E \cdot d{s}=-eEd
\Delta U=-1.6 \times 10^{-19}(850)(2.5)=-3.4 \times 10^{-16} \mathrm{~J}
\cdot
\cdot
d\vec{s}
\vec{E}
-
-
\text{initial}
\text{final}
\text{Answer A}
\text{The figure shows a plot for the electric field $E_x$ as a function of $x$. Find the magnitude of the }
\text{potential difference between the points $x=2.00 \mathrm{~m}$ and $x=6.00 \mathrm{~m}$.}
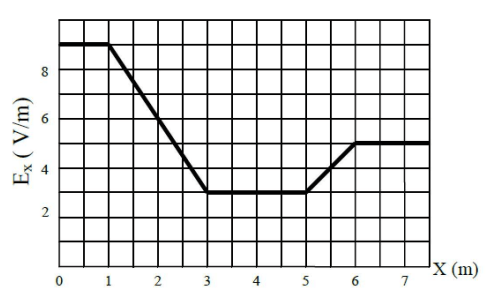
\text{A) 14.5 V}
\text{B) 12.5 V}
\text{C) 10.0 V}
\text{D) 16.5 V}
\text{E) 11.0 V}
\text{The figure shows a plot for the electric field $E_x$ as a function of $x$. Find the magnitude of the }
\text{potential difference between the points $x=2.00 \mathrm{~m}$ and $x=6.00 \mathrm{~m}$.}

\Delta V=-\int_i^{f} \vec{E} \cdot d \vec{s}
\Delta V=-
\text{Area under curve}
\text{Be careful: the area under the curve can be positive or negative}
\Delta V=-\int_{x_1}^{x_2} {E}_x \cdot d{x}
\text{(Warning: The question is incomplete: they need to precise that $E_y=E_z=0$)}
\Delta V=-14.5 V
\text{Answer A}
\text{In the figure, particles with charges $q_1=+10 \mu \mathrm{C}$ and $q_2=-30 \mu \mathrm{C}$ are fixed in place with }
\text{a separation of $d=24 \mathrm{~cm}$. }
\text{What is the value of $Q$ that will make the potential equal zero at point $P$.}
\cdot
\cdot
\cdot
Q
P
d
d
d
q_1
q_2
\times
\text{A) $7.1 \hspace{1mm}\mu \mathrm{C}$}
\text{B) $5.1 \hspace{1mm}\mu \mathrm{C}$}
\text{C) $10 \hspace{1mm}\mu \mathrm{C}$}
\text{D) $3.5 \hspace{1mm}\mu \mathrm{C}$}
\text{E) $4.5 \hspace{1mm}\mu \mathrm{C}$}
\text{In the figure, particles with charges $q_1=+10 \mu \mathrm{C}$ and $q_2=-30 \mu \mathrm{C}$ are fixed in place with }
\text{a separation of $d=24 \mathrm{~cm}$. }
\text{What is the value of $Q$ that will make the potential equal zero at point $P$.}
\cdot
\cdot
\cdot
Q
P
d
d
d
q_1
q_2
\times
V=\frac{k q_1}{r_1}+\frac{k q_2}{r_2}+\frac{k Q}{r_3}=0
\frac{k q_1}{d}+\frac{k q_2}{2d}+\frac{k Q}{\sqrt{2}d}=0
Q=\sqrt{2}(-q_1-\frac{q_2}{2})=\sqrt{2}(-10-(-30)/2)
Q=\sqrt{2}(5)=7.1\mu C
\sqrt{2}d
\text{Answer A}
\text{In a certain region of space, the electric potential is given by: $V=-2.0 x y z^2$, where $\mathrm{V}$ is in volts,}
\text{and $x, y$, and $z$ are in meters.
What is the magnitude of the electric field at the point with position}
\text{vector $(2.0 \hat{\imath}-2.0 \hat{\jmath}+4.0 \hat{k}) ?$}
\text{A) $111 \mathrm{~V} / \mathrm{m}$}
\text{B) $90.8 \mathrm{~V} / \mathrm{m}$}
\text{C) $16.1 \mathrm{~V} / \mathrm{m}$}
\text{D) $743 \mathrm{~V} / \mathrm{m}$}
\text{E) $571 \mathrm{~V} / \mathrm{m}$}
\text{In a certain region of space, the electric potential is given by: $V=-2.0 x y z^2$, where $\mathrm{V}$ is in volts,}
\text{and $x, y$, and $z$ are in meters.
What is the magnitude of the electric field at the point with position}
\text{vector $(2.0 \hat{\imath}-2.0 \hat{\jmath}+4.0 \hat{k}) ?$}
\begin{aligned}
& E_x=-\frac{\partial V}{\partial x}=2 y z^2=2(-2)(4)^2=-64 \mathrm{~N} / \mathrm{C} \\
& E_y=-\frac{\partial V}{\partial y}=2 x z^2=+64 \mathrm{~N} / \mathrm{C} \\
& E_z=-\frac{\partial V}{\partial z}=4 x y z=4(2)(-2)(4)=-64 \mathrm{~N} / \mathrm{C} \\
& E=\sqrt{E_x^2+E_y^2+E_z^2}=111 \mathrm{~V}
\end{aligned}
\text{Answer A}
\text{Four identical charged particles, each of charge $q=30 \mu \mathrm{C}$, are fixed at the corner of a square}
\text{of length $10.0 \mathrm{~cm}$. How much work is required, by an external agent, to move one of them to infinity?}
\text{A) -219 J}
\text{B) +219 J}
\text{C) -510 J}
\text{E) -105 J}
\text{D) +510 J}
\text{Four identical charged particles, each of charge $q=30 \mu \mathrm{C}$, are fixed at the corner of a square}
\text{of length $10.0 \mathrm{~cm}$. How much work is required, by an external agent, to move one of them to infinity?}
\Delta K=-\Delta U+W_{\text {app }}
0
W_{\text {app }}=\Delta U=q\Delta V =q(V_f-V_i)=-q(\frac{kq}{d}+\frac{kq}{d}+\frac{kq}{\sqrt{2}d})
0
W_{\text {app }}=-\frac{kq^2}{d}(2+\frac{1}{\sqrt{2}})=\frac{\left(9 \times 10^9\right)\left(30 \times 10^{-6}\right)^2}{0.1}\left(2+\frac{1}{\sqrt{2}}\right)
W_{\text {app }}=-219 \mathrm{~J}
\cdot
\cdot
\cdot
\cdot
d
d
d
d
\sqrt{2}d
\text{Answer A}
\text{Two metal spheres 1 and 2 with radii $r_1=1.0 \mathrm{~cm}$ and $r_2=2.0 \mathrm{~cm}$ carry charges $q_1=+22 \hspace{1mm}\mathrm{nC}$,}
\text{and $q_2=-10\hspace{1mm} \mathrm{ nC}$, respectively. Initially both spheres are far apart. Then the spheres are connected}
\text{by a thin wire, how much charge is lost by sphere 1 when the electrostatic equilibrium is reached?}
\text{A) $+18 \hspace{1mm}$nC}
\text{B) $-18 \hspace{1mm}$nC}
\text{C) $+12 \hspace{1mm}$nC}
\text{D) $-12 \hspace{1mm}$nC}
\text{E) $+14 \hspace{1mm}$nC}
\text{Two metal spheres 1 and 2 with radii $r_1=1.0 \mathrm{~cm}$ and $r_2=2.0 \mathrm{~cm}$ carry charges $q_1=+22 \hspace{1mm}\mathrm{nC}$,}
\text{and $q_2=-10\hspace{1mm} \mathrm{ nC}$, respectively. Initially both spheres are far apart. Then the spheres are connected}
\text{by a thin wire, how much charge is lost by sphere 1 when the electrostatic equilibrium is reached?}
22 \text{ nC}
q_1
q_2
\text{Connected}
\text{disonnected}
V_1=V_2
\text{since the spheres are conducting (metalic)}
\text{they will have the same electric potential }
\text{when connected}
-10 \text{ nC}
\text{Two metal spheres 1 and 2 with radii $r_1=1.0 \mathrm{~cm}$ and $r_2=2.0 \mathrm{~cm}$ carry charges $q_1=+22 \hspace{1mm}\mathrm{nC}$,}
\text{and $q_2=-10\hspace{1mm} \mathrm{ nC}$, respectively. Initially both spheres are far apart. Then the spheres are connected}
\text{by a thin wire, how much charge is lost by sphere 1 when the electrostatic equilibrium is reached?}
22 \text{ nC}
-10 \text{ nC}
q_1
q_2
\text{Connected}
\text{disonnected}
V_1=V_2
\text{since the spheres are conducting (metalic)}
\text{they will have the same electric potential }
\text{when connected}
\begin{aligned}
\frac{k q_1}{R_1} & =\frac{k q_2}{R_2}
\end{aligned}
V_1 =V_2
\Rightarrow
\text{The total charge is conserved:}
q_1+q_2=22-10=12 \text{ nC}=q_0
\begin{aligned}
\frac{k q_1}{R_1} & =\frac{k q_2}{R_2}
\end{aligned}
\Rightarrow
\begin{aligned}
{q_2} =q_1\frac{ R_2}{R_1}
\end{aligned}
\Rightarrow
\begin{aligned}
{q_2} =(q_0-q_2)\frac{ R_2}{R_1}
\end{aligned}
\Rightarrow
\begin{aligned}
{q_2} =q_0\frac{\frac{ R_2}{R_1}}{1+\frac{ R_2}{R_1}}=q_0\frac{ R_2}{R_1+ R_2}=12 \frac{2}{1+2}=8 \text{ nC},
\end{aligned}
q_1=12-8=4 \text{ nC}
\text{The charge lost by sphere $1$ is: } q_\text{lost}=22-4=18 \text{ nC}
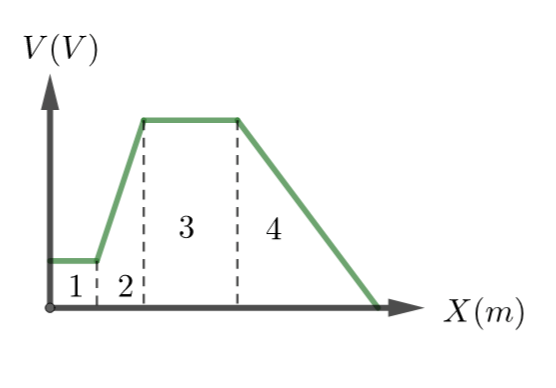
\text{FIG. 10 gives the electric potential V as a function of distance x . Rank the four regions according }
\text{to the magnitude of the x -component of the electric field within them, GREATEST FIRST.}
\text{A) 2, 4, then 1 and 3 tie}
\text{B) 4, 2, then 1 and 3 tie}
\text{C) $4,2,3,1$}
\text{D) $4,3,1,2$}
\text{E) $2,1,3,4$}
\text{FIG. 10 gives the electric potential V as a function of distance x . Rank the four regions according }
\text{to the magnitude of the x -component of the electric field within them, GREATEST FIRST.}
\text{A) 2, 4, then 1 and 3 tie}
\text{B) 4, 2, then 1 and 3 tie}
\text{C) $4,2,3,1$}
\text{D) $4,3,1,2$}
\text{E) $2,1,3,4$}

\text{The electric field component $E_x$ is the slope of $V(x)$}
Text
A) +260 V
B) -260 V
C) -195 V
D) +195 V
E) +325 V
\text{A uniform electric field of magnitude $325 \mathrm{~V} / \mathrm{m}$ is directed in the negative $y$ direction. The }
\text{coordinates of point A are $(-0.200,-0.300) \mathrm{m}$, and those of point B are $(0.400,0.500) \mathrm{m}$.}
\text{Calculate the electric potential difference $V_B-V_A$.}
\begin{aligned}
\Delta \mathrm{V} & =-\overrightarrow{\mathrm{E}} \cdot \Delta \overrightarrow{\mathrm{r}} \\
V_B & -V_A=-\overrightarrow{\mathrm{E}} \cdot\left(\overrightarrow{\mathrm{r}}_{\mathrm{B}}-\overrightarrow{\mathrm{r}}_{\mathrm{A}}\right) \\
& =325 \hat{\jmath} \cdot(0.6 \hat{\imath}+0.8 \hat{\jmath})=+260 \mathrm{~V}
\end{aligned}
Text
A) +260 V
B) -260 V
C) -195 V
D) +195 V
E) +325 V
\text{A uniform electric field of magnitude $325 \mathrm{~V} / \mathrm{m}$ is directed in the negative $y$ direction. The }
\text{coordinates of point A are $(-0.200,-0.300) \mathrm{m}$, and those of point B are $(0.400,0.500) \mathrm{m}$.}
\text{Calculate the electric potential difference $V_B-V_A$.}
\text{Proof:}
\Delta V=-\int \vec{E}\cdot \vec{ds}
\Delta V=-\int \vec{E}\cdot \vec{ds}=- \vec{E}\cdot \int\vec{ds}
=- \vec{E}\cdot \Delta \vec{r}
Chapter 24
By smstry
Chapter 24
- 518



