\displaystyle
\hat{H}_{\mathrm{R}}^{\mathrm{Q} 1 \mathrm{D}}=\frac{\hat{\mathbf{p}}^2}{2 m^*}+\frac{\alpha}{\hbar}(\hat{\boldsymbol{\sigma}} \times \hat{\mathbf{p}}) \cdot \mathbf{z}+V_{\text {conf }}(y),
\hat{H}=\hat{H}_{\mathrm{sb}}+\hat{H}_{\mathrm{mix}}+\hat{H}_{1 \mathrm{D}} \text { (Governale and Zülicke, 2004): }
\displaystyle \begin{aligned}
\hat{H}_{\mathrm{sb}} & =\frac{\hat{p}_y^2}{2 m^*}+V_{\mathrm{conf}}(y), \\
\hat{H}_{\mathrm{mix}} & =-\frac{\hbar k_{\mathrm{so}}}{m^*} \hat{\sigma}_x \hat{p}_y, \\
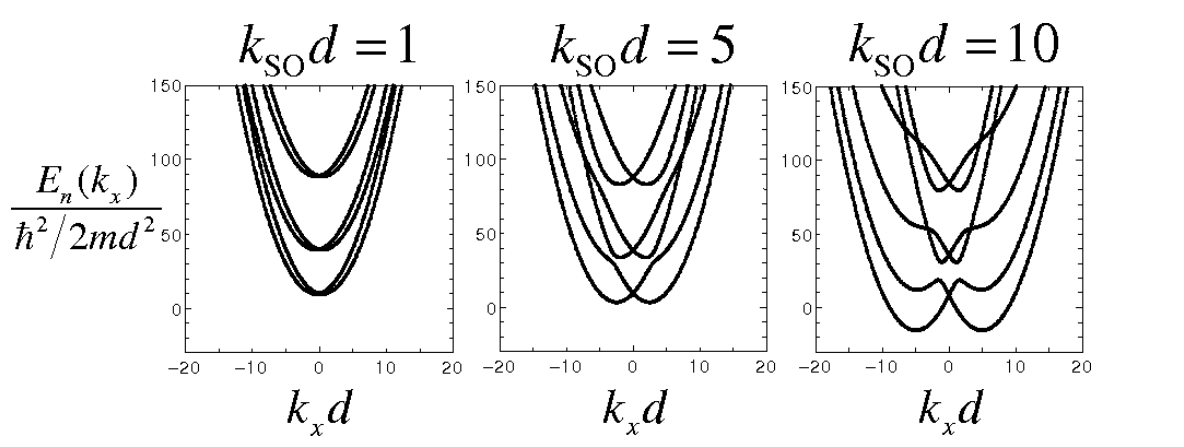
\hat{H}_{1 \mathrm{D}} & =\frac{\hbar^2}{2 m^*}\left(k_x+k_{\mathrm{so}} \hat{\sigma}_y\right)^2-\frac{\hbar^2 k_{\mathrm{so}}^2}{2 m^*} .
\end{aligned}
\displaystyle \alpha=\frac{\hbar^2 k_\text{so}}{m}
\text{for small spin-orbit coupling, we can discard the }\hat{H}_\text{mix} \text{ term.} \text{This equivalent than working }
\text{in a limit where the subands mixing is negligible, which is valid for }\displaystyle \frac{W}{L_\text{SO}}=\frac{k_\text{so}d}{\pi} \text{ is small}
\displaystyle i \frac{\partial}{\partial t} \psi=H \psi .
\psi=\psi_x \psi_y .
\displaystyle \psi_y=e^{-i E_n t} \Phi(y)
H=H_y+H_x
i\dot{\psi}_x \psi_y+i \psi_x \dot{\psi}_y=\left(H_y \psi_y\right) \psi_x+\left(H_x \psi_x\right) \psi_y
i \dot{\psi}_y=\left(H_y \psi_y\right)
\text{but we have}
\displaystyle i \frac{\partial}{\partial t}\psi_x=H_x \psi_x
\displaystyle \hat{H}=\frac{\hbar^2}{2 m^*}\left(k_x+k_{\mathrm{so}} \hat{\sigma}_y\right)^2-\frac{\hbar^2 k_{\mathrm{so}}^2}{2 m^*}
\displaystyle =\frac{\hbar^2k_x^2}{2 m^*}k_x^2+\alpha k_x \hat{\sigma}_y
\hat{H}=\hat{H}_{\mathrm{sb}}+\hat{H}_{\mathrm{mix}}+\hat{H}_{1 \mathrm{D}} \text { (Governale and Zülicke, 2004): }
\displaystyle \begin{aligned}
\hat{H}_{\mathrm{sb}} & =\frac{\hat{p}_y^2}{2 m^*}+V_{\mathrm{conf}}(y), \\
\hat{H}_{\mathrm{mix}} & =-\frac{\hbar k_{\mathrm{so}}}{m^*} \hat{\sigma}_x \hat{p}_y, \\
\hat{H}_{1 \mathrm{D}} & =\frac{\hbar^2}{2 m^*}\left(k_x+k_{\mathrm{so}} \hat{\sigma}_y\right)^2-\frac{\hbar^2 k_{\mathrm{so}}^2}{2 m^*} .
\end{aligned}
\displaystyle \alpha=\frac{\hbar^2 k_\text{so}}{m}
\displaystyle H_x=\frac{\hbar^2k_x^2}{2 m^*}+\alpha k_x \hat{\sigma}_y+J \Bigr(\vec{m}(t).\vec{\sigma}\Bigr)
\text{In the presence of a precessing magnetization, the hamiltonian becomes}
\displaystyle \psi_x(t)=e^{-\displaystyle i\int_0^t H_x(t)dt}\psi_x(0)= e^{-i \vec{a}.\vec{\sigma}}\psi_x(0)e^{-iE t}
\displaystyle \vec{a}=\alpha k_x t {\bf e_y}+J\int_0^t\vec{m}(t')dt'
\text { the velocity operator is } \hat{\mathbf{v}}=\hat{\mathbf{p}} / m^*-(\alpha / \hbar)\left(\hat{\sigma}_y \mathbf{e}_x-\hat{\sigma}_x \mathbf{e}_y\right) \text {. }
\displaystyle {j}^i=\frac{\hbar}{2} \psi^{\dagger}({r}) \frac{\hat{\sigma}_i \hat{{v}}+\hat{{v}} \hat{\sigma}_i}{2} \psi({r})
\text{Let us look at the z-projection of the spin flowing through the }x\text{ direction }
\displaystyle {j}^z=\frac{\hbar}{2} \psi^{\dagger}({r}) \frac{\hat{\sigma}_z \hat{{v}}_x+\hat{{v}}_x \hat{\sigma}_z}{2} \psi({r})
\text{The spin-orbit interaction brings two modifications in the problem:}
\text{1) an additional term in the velociy operator: because of the fact that }\sigma_z\sigma_y+\sigma_y\sigma_z=0
\text{this term doesn not modify the spin current along the z-axis}
\text{2) a modification in the wave function: this is seen in the term }\vec{a}. \\
\text{This modification will change the value of the pumped spin current}
\displaystyle {j}^z=\frac{\hbar}{2} \psi^{\dagger}({r}) \frac{\hat{\sigma}_z \hat{{v}}_x+\hat{{v}}_x \hat{\sigma}_z}{2} \psi({r})
\psi({r})=\Phi(y)e^{-iE_n t }\times e^{-i \vec{a}.\vec{\sigma}}\times u(0)e^{ik_x x}e^{-i Et}
\displaystyle {j}^z=|\Phi(y)|^2\frac{\hbar}{2} \times\frac{\hbar k_x}{m^*}\times u^{\dagger}({0})e^{\displaystyle i\vec{a}\vec{\sigma}} \hat{\sigma}_{z} e^{\displaystyle -i\vec{a}\vec{\sigma}}u({0})
\displaystyle e^{\displaystyle i\vec{a}\vec{\sigma}} \hat{\sigma}_{z} e^{\displaystyle -i\vec{a}\vec{\sigma}}=?
e^{\displaystyle i a(\hat{n} \cdot \vec{\sigma})} \vec{\sigma} e^{\displaystyle -i a(\hat{n} \cdot \vec{\sigma})}=\vec{\sigma} \cos (2a)+(\hat{n} \times \vec{\sigma}) \sin (2a)+\hat{n} (\hat{n} \cdot \vec{\sigma})(1-\cos (2a))
\displaystyle e^{\displaystyle i\vec{a}\vec{\sigma}} \hat{\sigma}_{z} e^{\displaystyle -i\vec{a}\vec{\sigma}}=?
e^{\displaystyle i a(\hat{n} \cdot \vec{\sigma})} {\sigma}_z e^{\displaystyle -i a(\hat{n} \cdot \vec{\sigma})}={\sigma}_z \cos (2a)+\vec{\sigma}\cdot(e_z\times\hat{n} ) \sin (2a)+\hat{n}_z (\hat{n} \cdot \vec{\sigma})(1-\cos (2a))
\displaystyle {j}^z_n=|\Phi_n(y)|^2\frac{\hbar}{2} \times\frac{\hbar k_x}{m^*}\times u^{\dagger}({0})e^{\displaystyle i\vec{a}\vec{\sigma}} \hat{\sigma}_{z} e^{\displaystyle -i\vec{a}\vec{\sigma}}u({0})
e^{\displaystyle i a(\hat{n} \cdot \vec{\sigma})} \vec{\sigma} e^{\displaystyle -i a(\hat{n} \cdot \vec{\sigma})}=\vec{\sigma} \cos (2a)+(\hat{n} \times \vec{\sigma}) \sin (2a)+\hat{n} (\hat{n} \cdot \vec{\sigma})(1-\cos (2a))
e^{\displaystyle i a(\hat{n} \cdot \vec{\sigma})} {\sigma}_z e^{\displaystyle -i a(\hat{n} \cdot \vec{\sigma})}={\sigma}_z \cos (2a)+\vec{\sigma}\cdot(e_z\times\hat{n} ) \sin (2a)+\hat{n}_z (\hat{n} \cdot \vec{\sigma})(1-\cos (2a))
\text{Let us suppose that we prepare the initial state as an eigenstate of }\hat{\sigma}_{z}
u(0)=(1,0)
u^{\dagger}({0})\hat{\sigma}_{z}u({0})=1
u^{\dagger}({0})\vec{\sigma}\cdot(e_z\times\hat{n} )u(0)=0
\text{because }(e_z\times\hat{n} )\text{ is perpendicular to }e_z
u^\dagger(0)\hat{n}_z (\hat{n} \cdot \vec{\sigma})u(0)=n_z^2
u^{\dagger}({0})\hat{\sigma}_{x}u({0})= u^{\dagger}({0})\hat{\sigma}_{y}u({0})=0
\displaystyle {j}^z_n=|\Phi_n(y)|^2\frac{\hbar}{2} \times\frac{\hbar k_x}{m^*}\times [ \hat{n}_z^2+(1-\hat{n}_z^2) \cos(2a)]
\displaystyle {j}^z=\frac{\hbar}{2} \times\frac{\hbar k_x}{m^*}\times [ \hat{n}_z^2+(1-\hat{n}_z^2) \cos(2a)]
\displaystyle {j}^z=\sum_n\displaystyle {j}^z_n
\text{let us express }a \text{ for large times}
\vec{m}(t)=\Big(m_0\sin(\omega t),m_0 \cos(\omega t), m_z\Big)
\displaystyle \int_0^t\vec{m}(t') dt'=\Big(\frac{m_0}{\omega}(1-\cos(\omega t)),\frac{m_0}{\omega} \sin(\omega t), m_z t\Big)
\displaystyle \vec{a}=\alpha k_x t {\bf e_y}+J\int_0^t\vec{m}(t')dt'
\displaystyle a=\sqrt{\Big[(\frac{Jm_0}{\omega}(1-\cos(\omega t)))^2+(\alpha k_x t+\frac{J m_0}{\omega} \sin(\omega t))^2+(Jm_z t)^2\Big]}
\text{at large times:}
\displaystyle a=\tilde{\omega} t+A \sin(\omega t)
\displaystyle \tilde{\omega}=\sqrt{\alpha^2 k_x^2+J^2m_z^2}
\displaystyle A=\frac{\alpha k_x}{\tilde{\omega}}\frac{J m_0}{\omega}
\displaystyle {j}^z=\frac{\hbar}{2} \times\frac{\hbar k_x}{m^*}\times [ \hat{n}_z^2+(1-\hat{n}_z^2) \cos(2a)]
\displaystyle n_z=\frac{J m_z}{\tilde{\omega}}
\displaystyle \cos\Big(2\tilde{\omega} t+2A \sin(\omega t)\Big)
\displaystyle \tilde{\omega}=\sqrt{\alpha^2 k_x^2+J^2m_z^2}
\displaystyle A=\frac{\alpha k_x}{\tilde{\omega}}\frac{J m_0}{\omega}
\displaystyle {j}^z=\frac{\hbar}{2} \times\frac{\hbar k_x}{m^*}\times [ \hat{n}_z^2+(1-\hat{n}_z^2) \cos(2a)]
\displaystyle n_z=\frac{J m_z}{\tilde{\omega}}
\text{Fourier transform of:}
\displaystyle
e^{A \sin x}=I_0(A)+2 \sum_{n \geq 0}(-1)^n I_{2 n+1}(A) \sin ((2 n+1) x)+2 \sum_{n \geq 1}(-1)^n I_{2 n}(A) \cos (2 n x)
\text{The Fourier series of $e^{A \sin x}$ is given by:}\\
\text{https://math.stackexchange.com/questions/1839071/fourier-transform-of-expa-sinx}
I_\alpha(x)=e^{-\alpha \pi i / 2} J_\alpha(i x)
\displaystyle \hat{f}(s)=\int_{-\infty}^\infty e^{is t} \cos[a t+i b \sin(c t)]dt=\frac{1}{2}\int_{-\infty}^\infty e^{i(s+a) t} e^{i b \sin(c t))}dt+\frac{1}{2}\int_{-\infty}^\infty e^{i(s+a) t} e^{i b \sin(c t))}dt
\displaystyle =\frac{1}{2}(\hat{g}(s+a)+\hat{g}(s-a))
\displaystyle \hat{g}(s)=\int_{-\infty}^\infty e^{is t} e^{i b \sin(c t))}dt= \frac{1}{c} \int_{-\infty}^\infty e^{is t'/c} e^{i b \sin( t'))} dt'
\displaystyle =\frac{1}{c}\hat{k}(s/c)
\displaystyle \hat{k}(s)= \int_{-\infty}^\infty e^{is t} e^{i b \sin( t))} dt
\displaystyle
=I_0(ib)-i2\pi \sum_{n \geq 0}(-1)^n I_{2 n+1}(ib) [\delta(s+(2n+1))-\delta(s-(2n+1))]
\displaystyle+2 \pi\sum_{n \geq 1}(-1)^n I_{2 n}(ib) [\delta(s+2n)+\delta(s-2n)]
\displaystyle \text{The frequencies are } nc\pm \text{ a and the amplitudes are }I_n(ib)
n\omega\pm2\tilde{\omega}
I_n(2iA)
\text{frequencies}
Work-with-Ousmane
By smstry
Work-with-Ousmane
- 168



