\text{Chapter 25}
\text{Chapter 25}
\text{Chapter 25}
\text{Chapter 25}


\frac{1}{C_{12}}=\frac{1}{C_1}+\frac{1}{C_2}
C_{12}=\frac{C_1 C_2}{C_1+C_2}
\Rightarrow
C_1, C_2 \text{are in series}
C_{\mathrm{eq}}=C_3+\frac{C_1 C_2}{C_1+C_2}=4.00 \mu \mathrm{F}+\frac{(10.0 \mu \mathrm{F})(5.00 \mu \mathrm{F})}{10.0 \mu \mathrm{F}+5.00 \mu \mathrm{F}}=7.33 \mu \mathrm{F}
\text { The equivalent capacitance is }
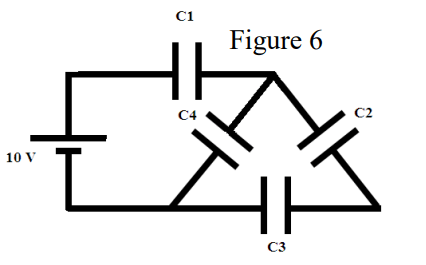
\text{Four capacitors, with capacitances $\mathrm{C}_1=3.0 \mu \mathrm{F}, \mathrm{C}_2=2.0 \mu \mathrm{F}, \mathrm{C}_3=5.0 \mu \mathrm{F}$, and $\mathrm{C}_4=$ $4.0 \mu \mathrm{F}$,}
\text{are connected in a circuit to a $10 \mathrm{~V}$ battery, as shown in Figure 6.}
\text{How much energy is stored by the combination?}
\text{A) $97 \hspace{1mm}\mu \mathrm{J}$}
\text{B) $64 \hspace{1mm}\mu \mathrm{J}$}
\text{C) $53 \hspace{1mm}\mu \mathrm{J}$}
\text{D) $59 \hspace{1mm}\mu \mathrm{J}$}
\text{E) $25 \hspace{1mm}\mu \mathrm{J}$}
\text{Four capacitors, with capacitances $\mathrm{C}_1=3.0 \mu \mathrm{F}, \mathrm{C}_2=2.0 \mu \mathrm{F}, \mathrm{C}_3=5.0 \mu \mathrm{F}$, and $\mathrm{C}_4=$ $4.0 \mu \mathrm{F}$,}
\text{are connected in a circuit to a $10 \mathrm{~V}$ battery, as shown in Figure 6.}
\text{How much energy is stored by the combination?}

C_1
C_2
C_3
C_4
10V
\Rightarrow
\text{Convince yourself that the circuit below }
\text{is equivalent to the original one.}
\text{Four capacitors, with capacitances $\mathrm{C}_1=3.0 \mu \mathrm{F}, \mathrm{C}_2=2.0 \mu \mathrm{F}, \mathrm{C}_3=5.0 \mu \mathrm{F}$, and $\mathrm{C}_4=$ $4.0 \mu \mathrm{F}$,}
\text{are connected in a circuit to a $10 \mathrm{~V}$ battery, as shown in Figure 6.}
\text{How much energy is stored by the combination?}

\text { Series: } C_{23}=\frac{C_2 C_3}{C_2+C_3}=\frac{10}{7} \hspace{1mm}\mu \mathrm{F}
\text { Parallel: } C_{234}=C_{23}+C_4=\frac{10}{7}+4=\frac{38}{7} \hspace{1mm}\mu \mathrm{F}=5.4 \hspace{1mm}\mu \mathrm{F}
C_{e q}=\frac{C_{234} \times C_1}{C_{234}+C_1}=\frac{5.4 \times 3.0}{5.4+3.0}=19.3 \hspace{1mm}\mu \mathrm{F}
\begin{aligned}
U & =\frac{1}{2} C_{e q} \cdot V^2 \\
& =\frac{1}{2} \times 1.93 \times 10^{-6} \times 100 \\
& =9.7 \times 10^{-5} \mathrm{~J}=97 \hspace{1mm}\mu \mathrm{J}
\end{aligned}
C_1
C_2
C_3
C_4
10V
\Rightarrow
\text{Convince yourself that the circuit below }
\text{is equivalent to the original one.}
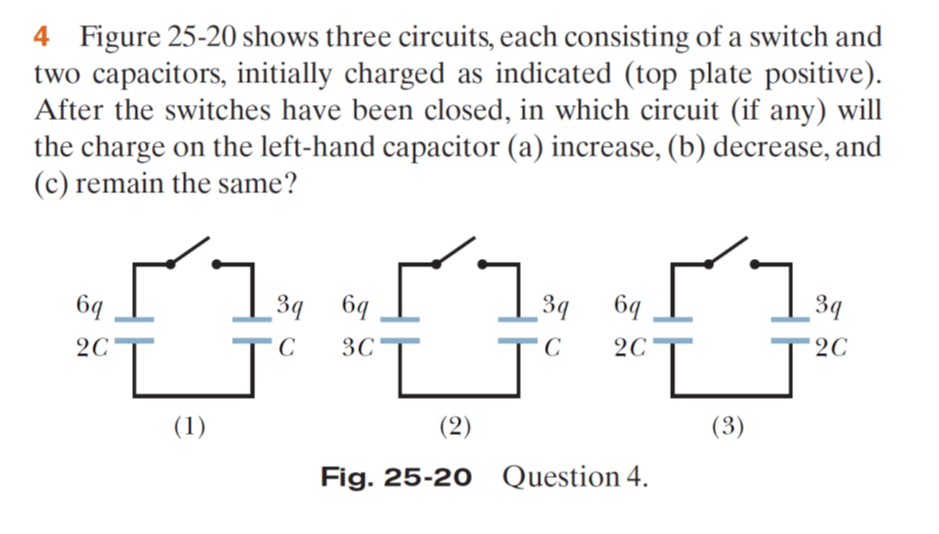
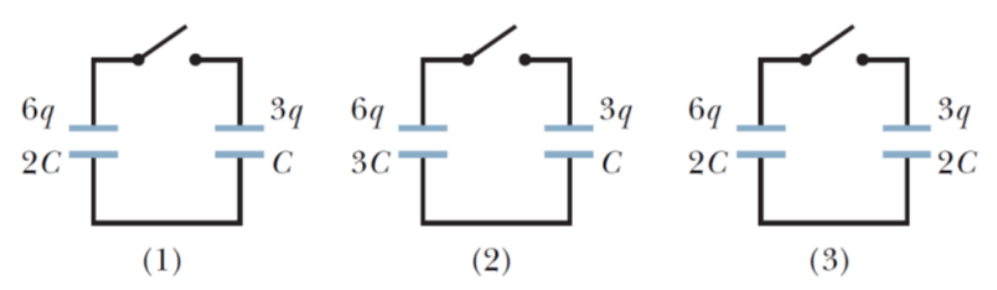
\text{After closing the switch:}
V=\frac{q'_1}{C_1}=\frac{q'_2}{C_2}=\frac{q'_1+q'_2}{C_1+C_2}=\frac{q_0}{C_1+C_2}
{q'_1}=q_0\frac{C_1}{C_1+C_2}
{q'_2}=q_0\frac{C_2}{C_1+C_2}
\text{in 3 cases } q_0=6q+3q=9q
q'_1
q'_2
6q
3q
\frac{27}{4}q
\frac{9}{4}q
\frac{9}{2}q
\frac{9}{2}q
\text{Case 1}
\text{Case 2}
\text{Case 3}
\text{remains the same}
\text{increases}
\text{decreases}

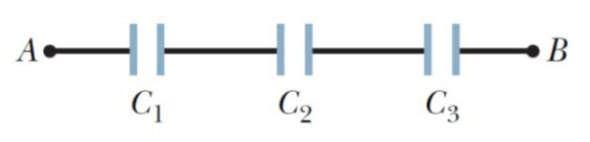
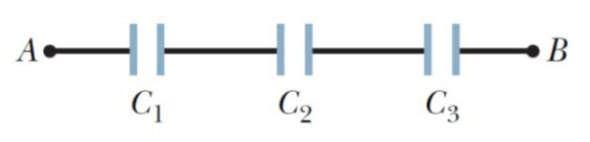
\text{The three capacitors are in series.}
\text{so, they have the same charge $q$}
q
q
q
-q
-q
-q
\text{the voltage on each capacitor is }
V_i=\frac{q}{C_i}
\text{so, the capacitor with the smallest capacitance $C_i$ will have the highest voltage}
\text{so the first to breakdown is $C_1$ when its voltage reaches $V_1=100V$ }
q=C_1V_1=10\times 10^{-6}\times 100=10^{-3}C
V_2=\frac{q}{C_2}=\frac{10^{-3}}{20\times 10^{-6}}=50V
V_3=\frac{q}{C_3}=\frac{10^{-3}}{25\times 10^{-6}}=40V
\text{We then deduce:}
V=V_1+V_2+V_3=100+50+40=190V
b) \text{The maximum energy that can be stored is the sum of energies in each capacitor}
U_\text{tot}=\frac{q^2}{2C_1}+\frac{q^2}{2C_2}+\frac{q^2}{2C_3}=0.095 J
\text{we can also use:}
U_\text{tot}=\frac{q^2}{2C_\text{eq}}
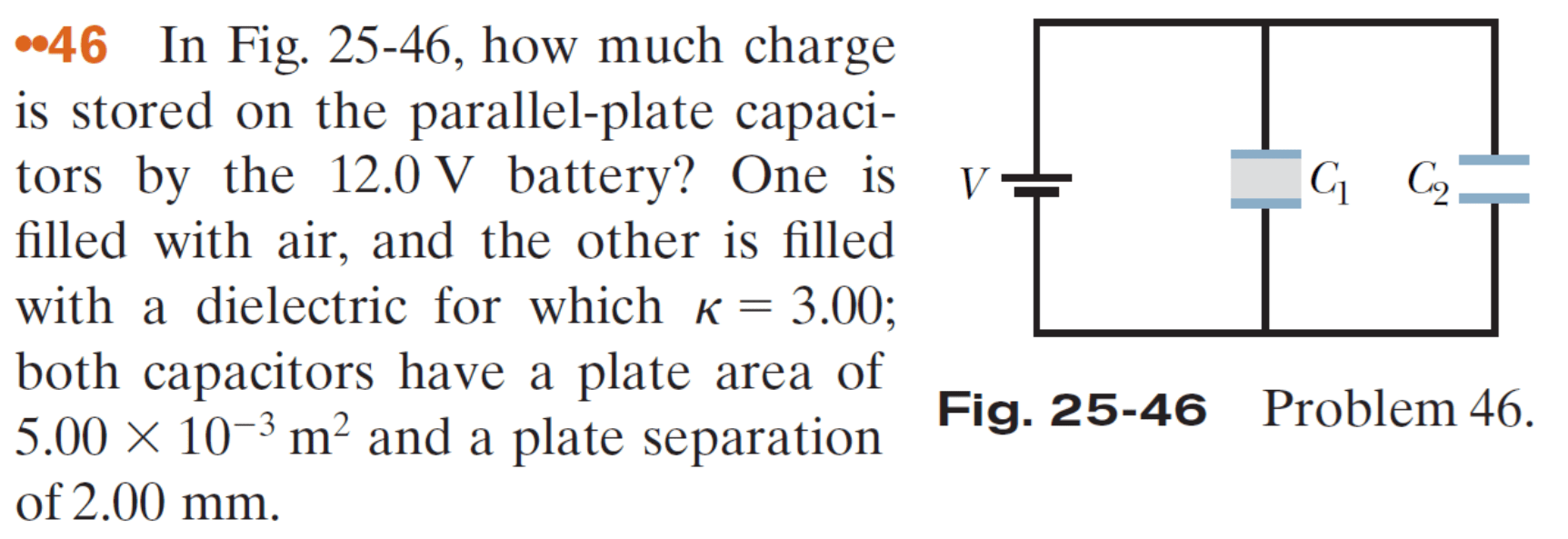
\text{An air-filled parallel-plate capacitor, whose capacitance is $13.5 \mathrm{pF}$, is charged using a battery }
\text{to a potential difference of $12.5 \mathrm{~V}$ across its plates. The charging battery is now disconnected }
\text{and a dielectric slab $(\kappa=6.50)$ is inserted between the plates.}
\text{What is the stored energy in the capacitor after the slab is inserted?}
\text{A) 162 \hspace{1mm} pJ}
\text{B) 154\hspace{1mm} nJ}
\text{C) 222 \hspace{1mm}nJ}
\text{D) 476\hspace{1mm} pJ}
\text{E) 111\hspace{1mm} pJ}
\text{An air-filled parallel-plate capacitor, whose capacitance is $13.5 \mathrm{pF}$, is charged using a battery }
U_f=\frac{Q^2}{2 C_\text{f}}=\frac{\left(168.75 \times 10^{-12}\right)^2}{2 \times 87.75 \times 10^{-12}}=1.62 \times 10^{-10} J=162 \times 10^{-12} J=162 \hspace{1mm}\mathrm{pJ}
\text{to a potential difference of $12.5 \mathrm{~V}$ across its plates. The charging battery is now disconnected }
\text{and a dielectric slab $(\kappa=6.50)$ is inserted between the plates.}
\text{What is the stored energy in the capacitor after the slab is inserted?}
\mathrm{C}_{\mathrm{f}}=\kappa \mathrm{C}_{\mathrm{i}}=6.5 \times 13.5=87.75\hspace{1mm} \mathrm{ pF}
\text{Charge is conserved: $Q=C_i V_i=13.5 \times 12.5=168.75 \hspace{1mm}p C$}
\text{An air filled parallel plate capacitor has capacitance of $\mathrm{C}=20.0 \mu \mathrm{F}$. If the lower half of the }
\text{capacitor is filled with dielectric material $\kappa=10$, as shown in FIGURE 10, find the }
\text{capacitance of the new capacitor.}
\text{A) $110 \hspace{1mm}\mu \mathrm{F}$}
\text{B) $9.09\hspace{1mm} \mu \mathrm{F}$}
\text{C) $440 \hspace{1mm}\mu \mathrm{F}$}
\text{D) $73.5 \hspace{1mm}\mu \mathrm{F}$}
\text{E) $173 \hspace{1mm}\mu \mathrm{F}$}
C=20\hspace{1mm}\mu F
L
\frac{L}{2}
\text{An air filled parallel plate capacitor has capacitance of $\mathrm{C}=20.0 \mu \mathrm{F}$. If the lower half of the }
\text{capacitor is filled with dielectric material $\kappa=10$, as shown in FIGURE 10, find the }
\text{capacitance of the new capacitor.}
\begin{aligned}
C & =20 \mu F=\varepsilon_0 A / d \\
C_\text{eq} & =C_1+C_2 \\
& =\varepsilon_0 \frac{A / 2}{d}+k \varepsilon_0 \frac{A / 2}{d} \\
& =\frac{1}{2} \varepsilon_0 \frac{A}{d}+\frac{k}{2} \varepsilon_0 \frac{A}{d} \\
& =\frac{1}{2} \times 20+\frac{10}{2}(20)=10+100=110 \hspace{1mm}\mu F
\end{aligned}
\text{equivalent to two capacitors}\\
\text{in parallel}
\text{A) $110 \hspace{1mm}\mu \mathrm{F}$}
\text{B) $9.09\hspace{1mm} \mu \mathrm{F}$}
\text{C) $440 \hspace{1mm}\mu \mathrm{F}$}
\text{D) $73.5 \hspace{1mm}\mu \mathrm{F}$}
\text{E) $173 \hspace{1mm}\mu \mathrm{F}$}
C=20\hspace{1mm}\mu F
L
\frac{L}{2}
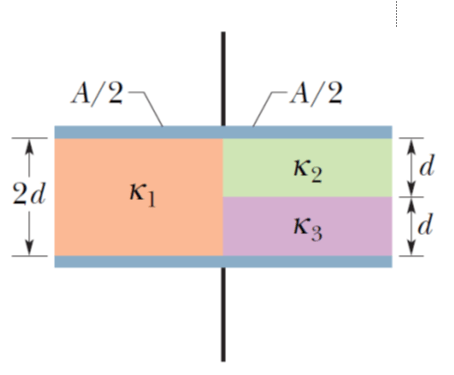
\text{Figure 1 shows a parallel-plate capacitor of plate area $A=10.5 \mathrm{~cm}^2$ and plate separation }
\text{$2 d=7.12 \mathrm{~mm}$. The left half of the gap is filled with material of dielectric constant $\kappa_1=21.0$;}
\text{the top of the right half is filled with material of dielectric constant $\kappa_2=42.0$; the bottom of }
\text{the right half is filled with material of dielectric constant $\kappa_3=$ 58.0. What is the capacitance?}

\text{Figure 1 shows a parallel-plate capacitor of plate area $A=10.5 \mathrm{~cm}^2$ and plate separation }
\text{$2 d=7.12 \mathrm{~mm}$. The left half of the gap is filled with material of dielectric constant $\kappa_1=21.0$;}
\text{the top of the right half is filled with material of dielectric constant $\kappa_2=42.0$; the bottom of }
\text{the right half is filled with material of dielectric constant $\kappa_3=$ 58.0. What is the capacitance?}
\kappa_1
\kappa_2
\kappa_3
\text{The equivalent system is: }

\text{Figure 1 shows a parallel-plate capacitor of plate area $A=10.5 \mathrm{~cm}^2$ and plate separation }
\text{$2 d=7.12 \mathrm{~mm}$. The left half of the gap is filled with material of dielectric constant $\kappa_1=21.0$;}
\text{the top of the right half is filled with material of dielectric constant $\kappa_2=42.0$; the bottom of }
\text{the right half is filled with material of dielectric constant $\kappa_3=$ 58.0. What is the capacitance?}
\kappa_1
\kappa_2
\kappa_3
\text{The equivalent system is: }
C_\text{eq}={C_1+\frac{C
_2C_3}{C_2+C_3}}
\text{$C_2$, $C_3$ are in series and their equivalent capacitor is in parallel with $C_1$}
C_\text{23}= {\frac{C
_2C_3}{C_2+C_3}}
\text{let us put: }C_0=\frac{\epsilon_0 A}{d}
C_1=\kappa_1 \frac{C_0}{4}
C_2=\kappa_2 \frac{C_0}{2}
C_3=\kappa_3 \frac{C_0}{2}
C_\text{eq}={\frac{\kappa_1}{4}C_0+\frac{1}{2}\frac{\kappa_2 C
_0 \kappa_3C_0}{\kappa_2C_0+\kappa_3C_0}}=\left(\frac{\kappa_1}{4}+\frac{1}{2}\frac{\kappa_2 \kappa_3}{\kappa_2+\kappa_3}\right) C_0=4.55\times10^{-11}F
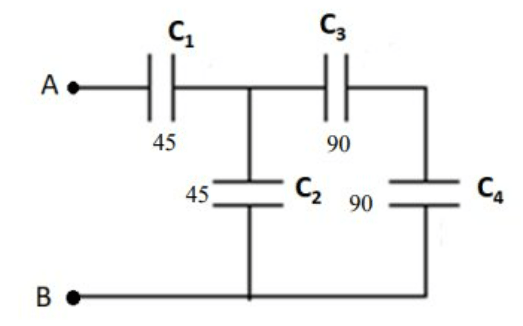
\text{In the circuit diagram shown in Figure 5, the capacitance of the capacitors are $\mathrm{C}_1=$ $\mathrm{C}_2=45 \mu \mathrm{F}$ }
\text{and $\mathrm{C}_3=\mathrm{C}_4=90 \mu \mathrm{F}$.}
\text{Find the potential difference between points $\mathrm{A}$ and $\mathrm{B}$ $\left(\mathrm{V}_{\mathrm{AB}}\right)$ if the charge on capacitor $\mathrm{C}_1$ is $60 \mu \mathrm{C}$.}
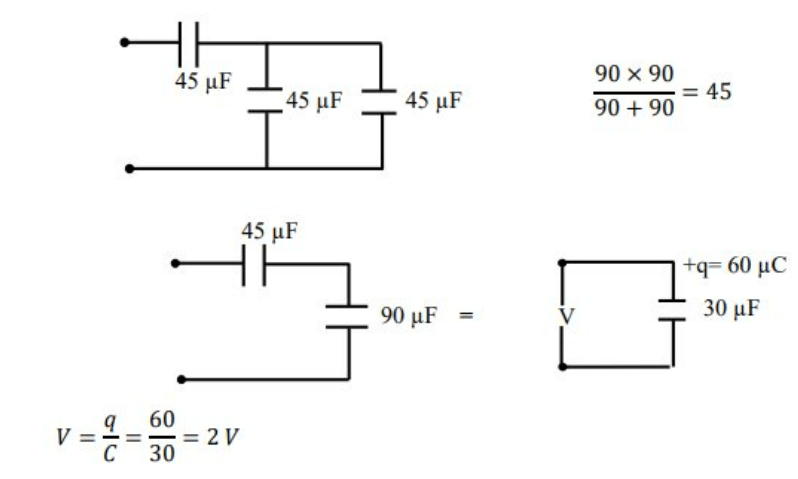
\text{A) 2.0 V}
\text{B) 1.3 V}
\text{C) 4.5 V}
\text{D) 5.4 V}
\text{E) 6.8 V}
\text{In the circuit diagram shown in Figure 5, the capacitance of the capacitors are $\mathrm{C}_1=$ $\mathrm{C}_2=45 \mu \mathrm{F}$ }
\text{and $\mathrm{C}_3=\mathrm{C}_4=90 \mu \mathrm{F}$.}
\text{Find the potential difference between points $\mathrm{A}$ and $\mathrm{B}$ $\left(\mathrm{V}_{\mathrm{AB}}\right)$ if the charge on capacitor $\mathrm{C}_1$ is $60 \mu \mathrm{C}$.}

\text{In the capacitor circuit shown in FIGURE 6, the capacitance of each capacitor is C. }
\text{Find the ratio of $Q_3 / Q_2$.}
C_1
C_2
C_5
V
C_4
C_3
\text{Figure 6}
A) 2
B)1/2
C)1/3
D)3
E)2/3
\text{In the capacitor circuit shown in FIGURE 6, the capacitance of each capacitor is C. }
\text{Find the ratio of $Q_3 / Q_2$.}
\text{We have $\mathrm{V}_3=\mathrm{V} \quad \Rightarrow \mathrm{Q}_3=\mathrm{C_3V}=CV$}
\mathrm{V}=\mathrm{V}_1+\mathrm{V}_2 \quad \Rightarrow \quad V=\frac{Q_1}{C_1}+\frac{Q_2}{C_2}=\frac{Q_1+Q_2}{C}
\text{The capacitors are in series, so: $\mathrm{Q}_1=\mathrm{Q}_2$}
\text{Equation \textcircled{\raisebox{-0.9pt}{2}} becomes: $\displaystyle V=2 \frac{Q_2}{C}$}
\text{$\textcircled{\raisebox{-0.9pt}{1}}$ And \textcircled{\raisebox{-0.9pt}{3}} lead to: $\displaystyle \frac{Q_3}{Q_2}=2$}
\cdots \textcircled{\raisebox{-0.9pt}{1}}
\cdots \textcircled{\raisebox{-0.9pt}{2}}
\cdots \textcircled{\raisebox{-0.9pt}{3}}
C_1
C_2
C_5
V
C_4
C_3
\text{Figure 6}
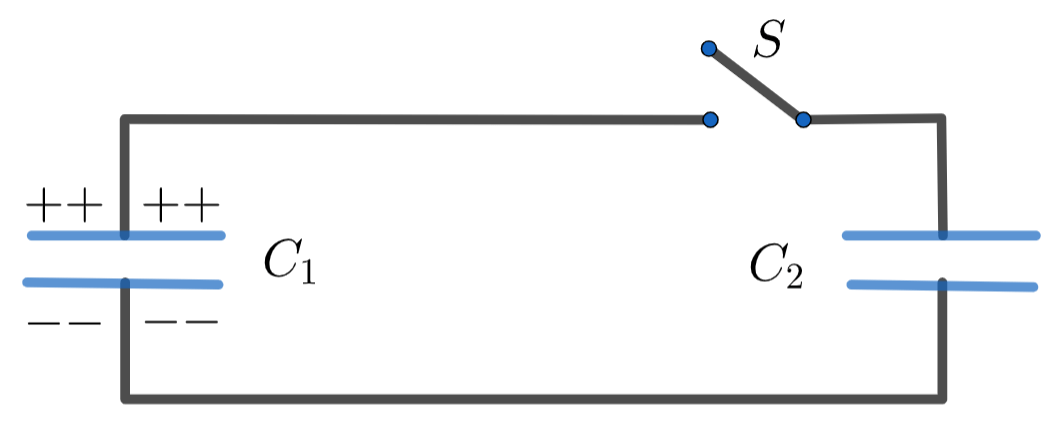
\text{In FIGURE 9, the capacitors $C_1=2.0 \mu \mathrm{F}$ and $C_2=4.0 \mu \mathrm{F}$. The capacitor $\mathrm{C}_1$ is charged to }
\text{a potential difference of 10 V and $C_2$ is initially uncharged. After closing the switch $S$, find }
\text{the total energy stored by the two capacitors.}
A)\hspace{1mm} 3.3 \times 10^{-5}\text{ J}
B)\hspace{1mm} 1.0 \times 10^{-5}\text{ J}
C)\hspace{1mm} 3.0 \times 10^{-5}\text{ J}
D)\hspace{1mm} 1.5 \times 10^{-5}\text{ J}
E)\hspace{1mm} 5.0 \times 10^{-5}\text{ J}
\text{In FIGURE 9, the capacitors $C_1=2.0 \mu \mathrm{F}$ and $C_2=4.0 \mu \mathrm{F}$. The capacitor $\mathrm{C}_1$ is charged to }
\text{a potential difference of 10 V and $C_2$ is initially uncharged. After closing the switch $S$, find }
\text{the total energy stored by the two capacitors.}
\begin{aligned}
& Q_1=C_1 V=2 \times 10^{-6} \times 10=20 \mu \mathrm{C} \\
& Q_T=Q_1=20 \mu \mathrm{C} \\
& E_T=\frac{1}{2} \frac{q^2}{C_T}=\frac{1}{2} \frac{\left(20 \times 10^{-6}\right)^2}{6 \times 10^{-6}}=3.33 \times 10^{-5} \mathrm{~J}
\end{aligned}
A)\hspace{1mm} 3.3 \times 10^{-5}\text{ J}
B)\hspace{1mm} 1.0 \times 10^{-5}\text{ J}
C)\hspace{1mm} 3.0 \times 10^{-5}\text{ J}
D)\hspace{1mm} 1.5 \times 10^{-5}\text{ J}
E)\hspace{1mm} 5.0 \times 10^{-5}\text{ J}

\text{Remark: Although someone might think that the energy is conserved and thus $E=\frac{1}{2} C_1 V^2$}
\text{this is not true because equilibrium can not be reached without a small resistance that }
\text{dessipates energy}

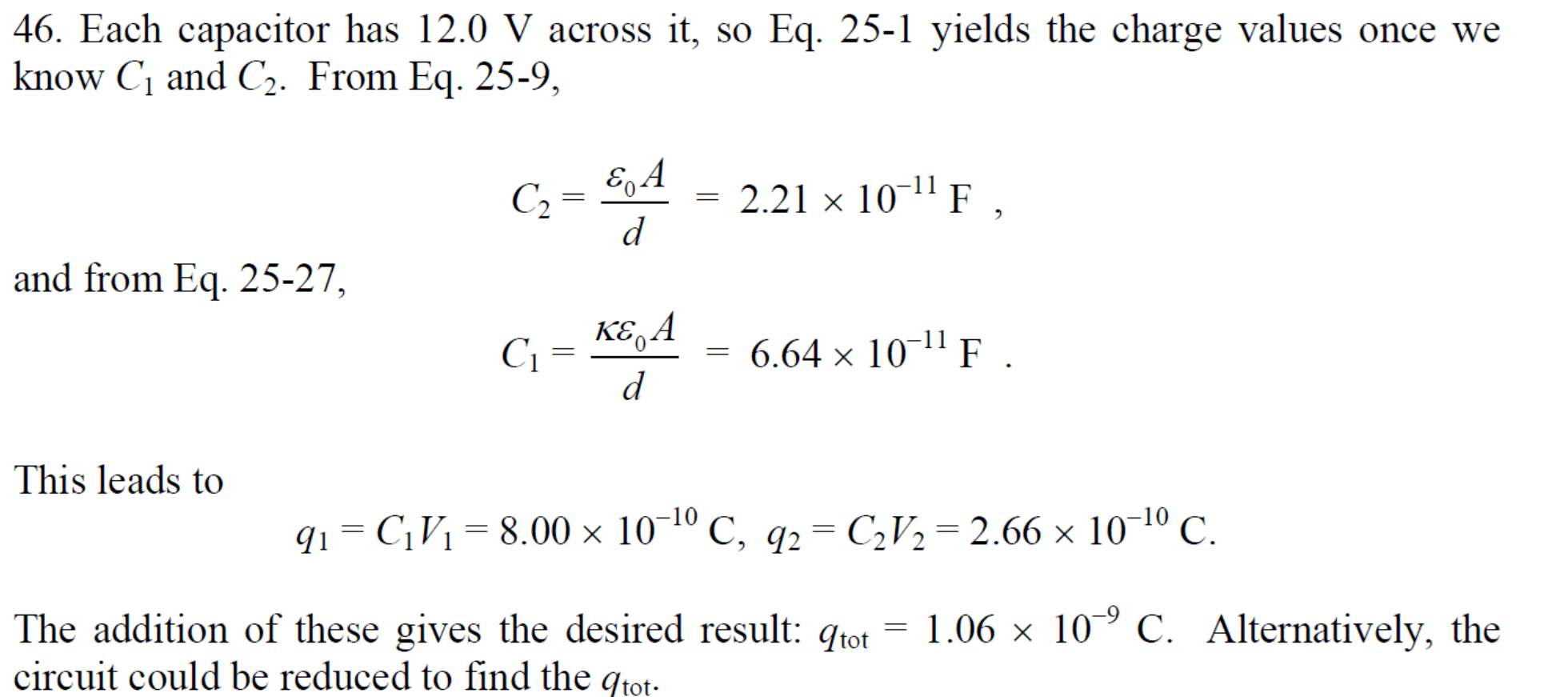
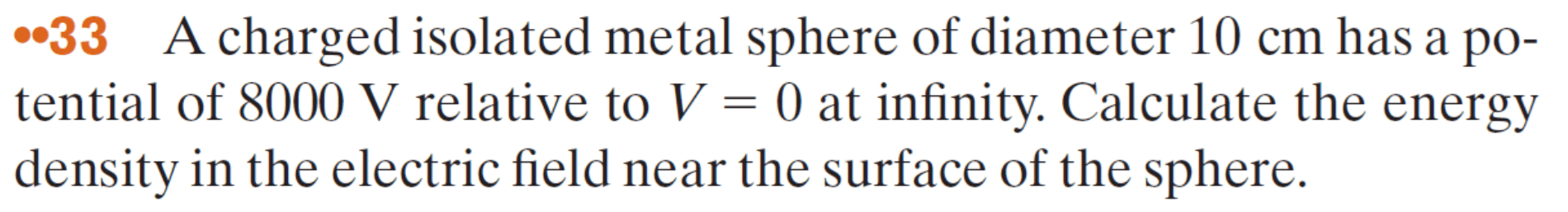
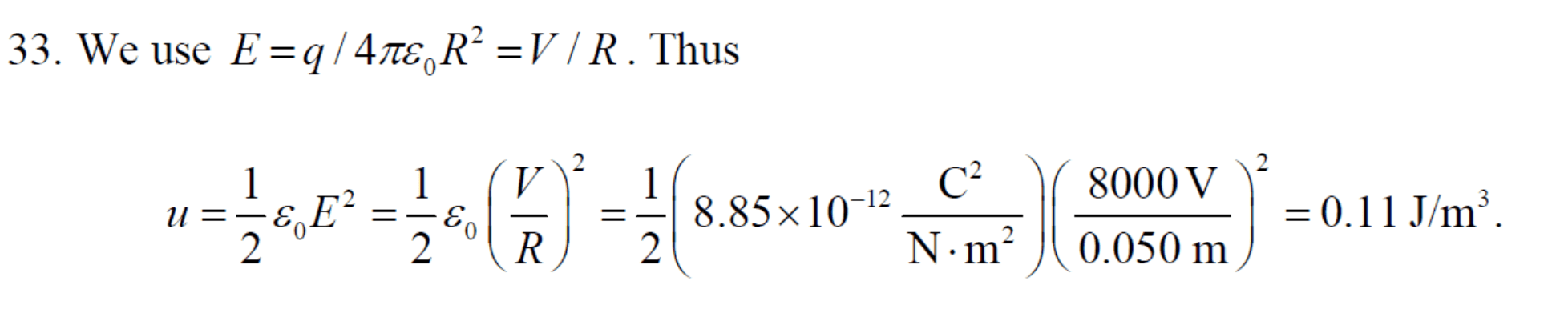
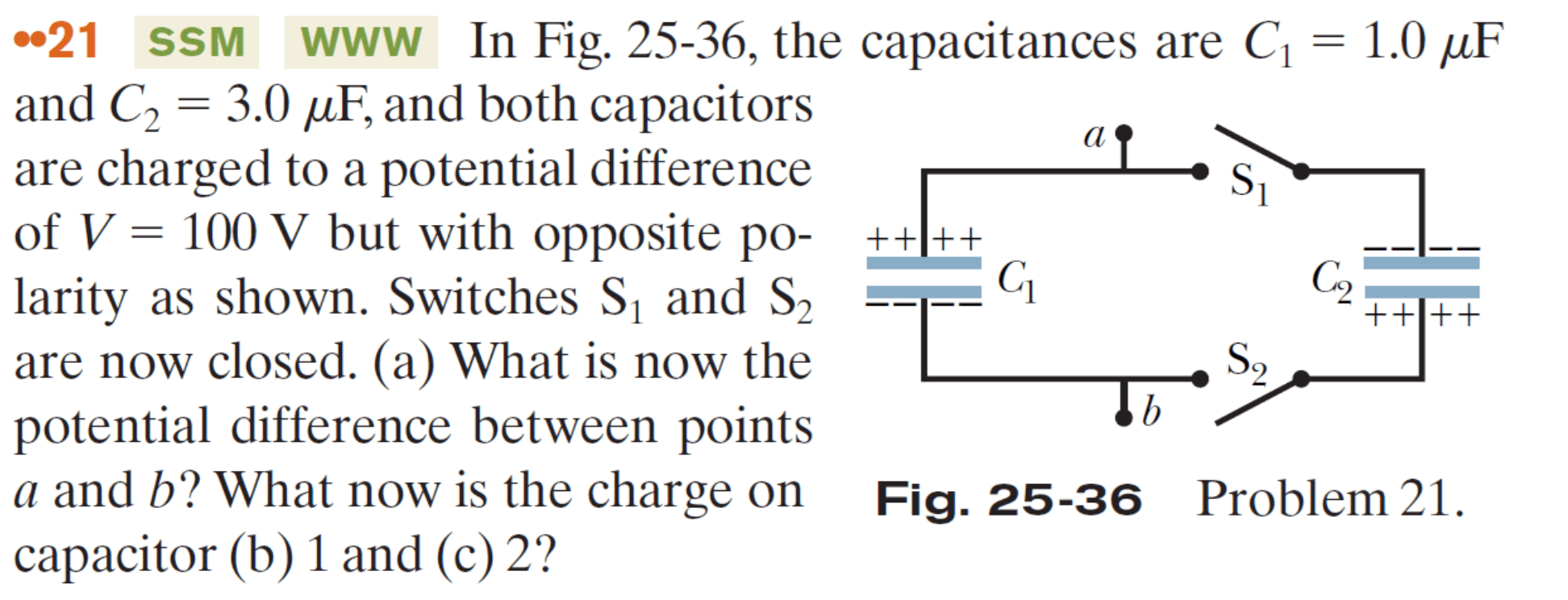

\text{After closing the swithches, we will have the same voltage across the two capacitors}
\text{Let us call the new charges $q'_1$, $q'_2$}
V=\frac{q'_1}{C_1}=\frac{q'_2}{C_2}=\frac{q'_1+q'_2}{C_1+C_2}=\frac{q_0}{C_1+C_2}
q_0=q'_1+q'_2=q_2-q_1
{q'_1}=q_0\frac{C_1}{C_1+C_2}
{q'_2}=q_0\frac{C_2}{C_1+C_2}
=C_2V_0-C_1V_0
=2\times 10^{-4}C
{q'_1}=2\times 10^{-4}\frac{1}{1+3}=50 \mu C
{q'_2}=2\times 10^{-4}\frac{3}{1+3}=150 \mu C
\text{initial}
\text{final}
\text{
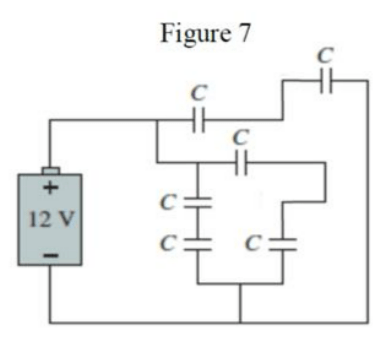
A total of $1.1 \times 10^{-4} \mathrm{~J}$ of energy is stored in six identical capacitors each with capacitance $C$ }
\text{and connected as shown in Figure 7. How much charge is stored in each capacitor?}
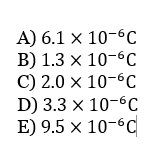
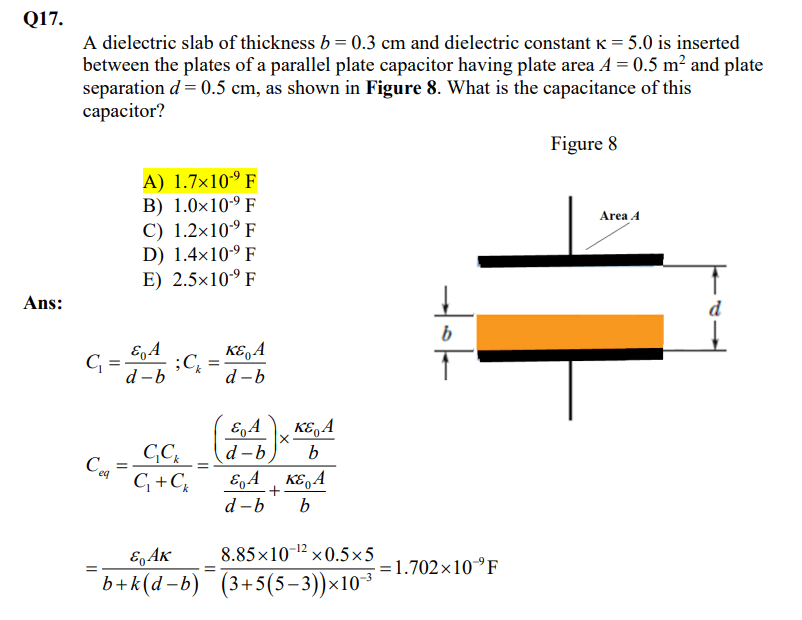
Chapter 25
By smstry
Chapter 25
- 576



