\text{Chapter 27}
\text{Chapter 27}
\text{Chapter 27}
\text{Chapter 27}
\text{Five resistors are connected as shown in FIGURE 5. The potential difference between }
\text{points $\mathbf{A}$ and $\mathbf{B}$ is $25.0 \mathrm{~V}$. What is the current through the $1.80$ $ \Omega$ resistor?}



3.60 \text{ }\Omega
3.50 \text{ }\Omega
1.80 \text{ }\Omega
I


2.40 \text{ }\Omega
5.10 \text{ }\Omega
I_1
I_2
\xi
A
B
\text{A) 2.76 A}
\text{B) 3.34 A}
\text{C) 1.67 A}
\text{D) 0.577 A}
\text{E) 2.09 A}
\text{Five resistors are connected as shown in FIGURE 5. The potential difference between }
\text{points $\mathbf{A}$ and $\mathbf{B}$ is $25.0 \mathrm{~V}$. What is the current through the $1.80$ $ \Omega$ resistor?}
I=\frac{25.0}{3.60+2.40+1.49}=3.34 \mathrm{~A}
\begin{aligned}
& \xi-3.60 \mathrm{I}-1.80 \mathrm{I}_1-2.40 \mathrm{I}=0 \\
& \Rightarrow \mathrm{I}_1=\frac{\varepsilon-6 \mathrm{I}}{1.8}=\frac{25-(6 \times 3.34)}{1.8}=2.76 \mathrm{~A}
\end{aligned}
\text{Now, consider loop 1:}\\
\text{(We used the equivalent resistance)}
\text{Answer A}



3.60 \text{ }\Omega
3.50 \text{ }\Omega
1.80 \text{ }\Omega
I


2.40 \text{ }\Omega
5.10 \text{ }\Omega
I_1
I_2
\xi
A
B


3.60 \text{ }\Omega
I

2.40 \text{ }\Omega
\xi
A
B
1.49 \hspace{1mm}\Omega
\circlearrowright
1
\text{In the circuit shown in FIGURE 6, the current $\boldsymbol{I}=0.36 \mathrm{~A}$.}
\text{What is the potential difference $\boldsymbol{V}_A-\boldsymbol{V}_B$ ?}



5.0 \text{ }\Omega
5.0 \text{ }\Omega
3.0 \text{ }\Omega
8.0 \text{ }V
4.0 \text{ }V
I_x
I
\cdot
\cdot
A
B
\text{A) $+$2.9 V}
\text{B) $+$1.1 V}
\text{C) $-$1.1 V}
\text{D) $-$2.9 V}
\text{E) $-$4.7 V}
\text{In the circuit shown in FIGURE 6, the current $\boldsymbol{I}=0.36 \mathrm{~A}$.}
\text{What is the potential difference $\boldsymbol{V}_A-\boldsymbol{V}_B$ ?}
\begin{aligned}
& +8.0-3.0 \mathrm{I}-5.0 \mathrm{I}_{\mathrm{x}}=0 \\
& \Rightarrow \mathrm{I}_{\mathrm{x}}=\frac{8.0-3.0 \mathrm{I}}{5.0}=\frac{8.0-1.08}{5.0}=1.384 \mathrm{~A}
\end{aligned}
\begin{aligned}
& \mathrm{V}_{\mathrm{A}}+4.0-5.0 \mathrm{I}_{\mathrm{x}}=\mathrm{V}_{\mathrm{B}} \\
& \Rightarrow \mathrm{V}_{\mathrm{A}}-\mathrm{V}_{\mathrm{B}}=5.0 \mathrm{I}_{\mathrm{x}}-4.0=+2.9 \mathrm{~V}
\end{aligned}
\text{Now, proceed from $\mathrm{A} \rightarrow \mathrm{B}$ through the $4.0 \mathrm{~V}$ battery:}
\text{Consider Loop 1:}
\text{Answer A}



5.0 \text{ }\Omega
5.0 \text{ }\Omega
3.0 \text{ }\Omega
8.0 \text{ }V
4.0 \text{ }V
I_x
I
\cdot
\cdot
A
B
\circlearrowright
1
\text { Find the value of the } \operatorname{emf}(\mathrm{E}) \text { of the battery shown in Figure 6, if the current } \mathrm{I}=1.2 \mathrm{~A} \text {. }



5.0 \text{ }\Omega
10 \text{ }\Omega
4.0 \text{ }\Omega
\xi
15 \text{ }V
15 \text{ }V
I
\text{A) 1.8 V}
\text{B) 7.5 V}
\text{C) 3.8 V}
\text{D) 3.2 V}
\text{E) 4.3 V}
\text { Find the value of the } \operatorname{emf}(\mathrm{E}) \text { of the battery shown in Figure 6, if the current } \mathrm{I}=1.2 \mathrm{~A} \text {. }



5.0 \text{ }\Omega
10 \text{ }\Omega
4.0 \text{ }\Omega
\xi
15 \text{ }V
15 \text{ }V
I
\text{loop 3}

\begin{aligned}
& 15-5 \times 1.2+10 i_2-15=0 \Rightarrow i_2=0.6 \mathrm{~A} \\
& i_3=i_1+i_2=1.8 \mathrm{~A}
\end{aligned}
\underline{\text{loop 3}}
\begin{aligned}
& 15-5 \times 1.2-4 \times 1.8-\xi=0 \\
& \xi=1.8 \mathrm{~V}
\end{aligned}
\underline{\text{loop 1}}
i_1
i_2
i_3
\text{Answer A}
\circlearrowright
1
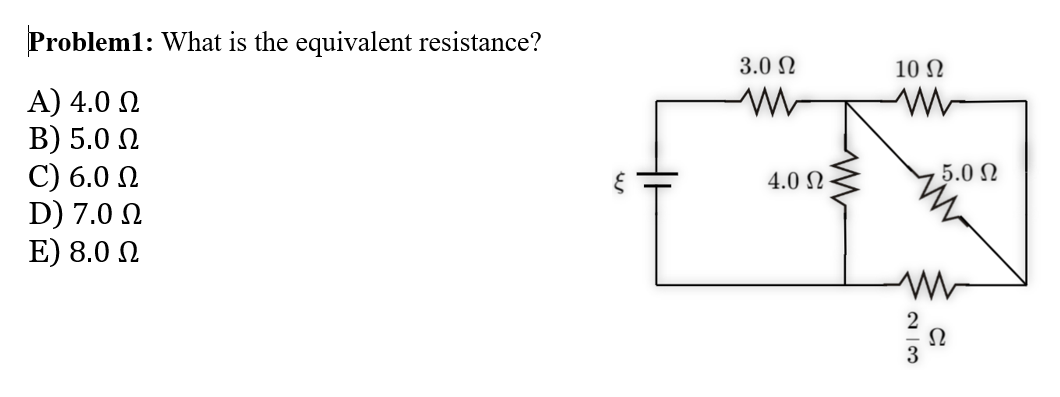
\text{In the circuit shown in Figure 7, what should be the ratio $\xi_3 / \xi_1$ if $\xi_1=\xi_2$ and the electric}
\text{current in the circuit equal to zero?}


\xi_1

\xi_2
\xi_3
+
+
+
-
-
-
R
R
R
\text{A) 2.0}
\text{B) 0.5}
\text{C) 1.0}
\text{D) 4.0}
\text{E) 0.25}
\text{In the circuit shown in Figure 7, what should be the ratio $\xi_3 / \xi_1$ if $\xi_1=\xi_2$ and the electric}
\text{current in the circuit equal to zero?}


\xi_1

\xi_2
\xi_3
+
+
+
-
-
-
R
R
R
\begin{aligned}
& \mathrm{i}=0 \Rightarrow \xi_1-\xi_3+\xi_2=0 \\
& \xi_1=\xi_2 \Rightarrow 2 \xi_1-\xi_3=0 \\
& \frac{\xi_3}{\xi_1}=2
\end{aligned}
\text{Answer A}
\text { Consider the circuit shown in FIGURE 6. Find the potential difference } V_a-V_b \text {. }




25.0\text{ } V
5.00 \text{ }\Omega
10.0 \text{ }\Omega
10.0 \text{ }\Omega
5.00 \text{ }\Omega
20.0\text{ } \Omega

\cdot
\cdot
a
b
\text{A) $-5.68 \hspace{1mm}V$}
\text{B) $+5.68\hspace{1mm} V$}
\text{C) $+44.3 \hspace{1mm}V$}
\text{D) $+19.3 \hspace{1mm}V$}
\text{E) $-19.3\hspace{1mm} V$}
\text { Consider the circuit shown in FIGURE 6. Find the potential difference } V_a-V_b \text {. }
\frac{1}{\mathrm{R}_{\mathrm{eq}}^*}=\frac{1}{25}+\frac{1}{5}+\frac{1}{10}=\frac{17}{50}
{\mathrm{R}_{\mathrm{eq}}^*}=\frac{50}{17}\hspace{1mm} \Omega=2.94 \text{ }\Omega
\Rightarrow
R_\text{eq}=10+2.94=12.94\text{ }\Omega
\mathrm{i}_{\text {Battery }}=\frac{25}{\mathrm{R}_{\mathrm{eq}}}=1.93 A
\begin{aligned}
& \mathrm{V}_{\mathrm{a}}-10 i_{\mathrm{B}}+25=\mathrm{V}_{\mathrm{b}} \\
& \mathrm{V}_{\mathrm{a}}-\mathrm{V}_{\mathrm{b}}=10 i_{\mathrm{B}}-25=-5.68 \mathrm{~V}
\end{aligned}
\text{Answer A}




25.0\text{ } V
5.00 \text{ }\Omega
10.0 \text{ }\Omega
10.0 \text{ }\Omega
5.00 \text{ }\Omega
20.0\text{ } \Omega

\cdot
\cdot
a
b
i_B
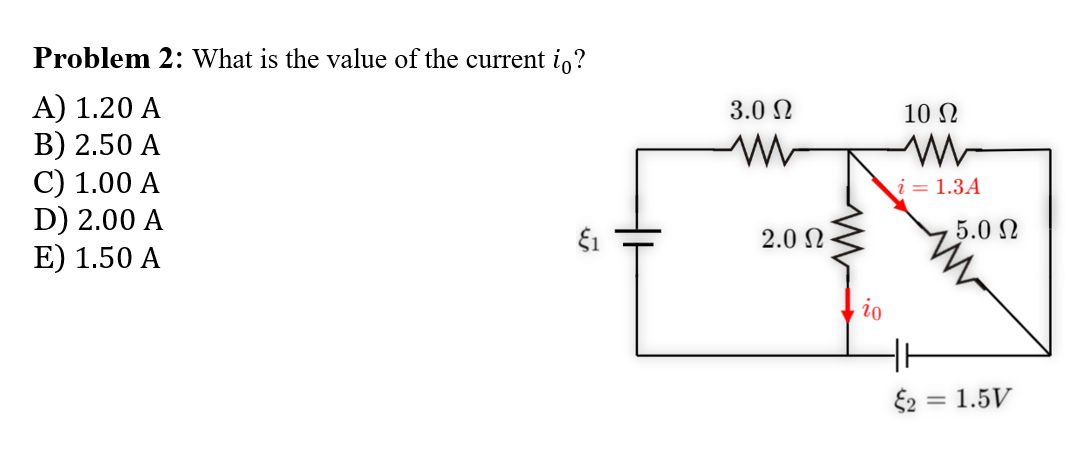
\text { For the circuit shown in FIGURE 7, what is the current in the upper } 20.0 \Omega \text { resistor? }






+
-
5.00 \text{ }\Omega
15.0 \text{ }\Omega
20.0 \text{ }\Omega
10.0 \text{ }\Omega
20.0 \text{ }\Omega
45.0 \text{ }V
10.0\text{ } \Omega
\text{A) 0.571 A}
\text{B) 0.643 A}
\text{C) 0.429 A}
\text{D) 1.290 A}
\text{E) 0.321 A}
\text { For the circuit shown in FIGURE 7, what is the current in the upper } 20.0 \Omega \text { resistor? }






+
-
5.00 \text{ }\Omega
15.0 \text{ }\Omega
20.0 \text{ }\Omega
10.0 \text{ }\Omega
20.0 \text{ }\Omega
45.0 \text{ }V
10.0\text{ } \Omega
\frac{1}{R_p}=\frac{1}{20}+\frac{1}{10}+\frac{1}{20}=\frac{1+2+1}{20}=\frac{4}{20} \Rightarrow R_p=5 \Omega
R_{e q}=5+15+5+10=35 \Omega
\mathrm{i}_{\text {Battery }}=\frac{45}{35}=\frac{9}{7} \mathrm{~A} ;
i_\text{Battery}
i
V=R_p i_\text{Battery}=5\times 9/7=6.43 \text{ V}
i=\frac{V}{20}=\frac{6.43}{20}=0.321\text{ A}
\text{The 3 resistors in parallel have the ssame $V$ as $R_p$:}
\text{The current through the 20 $ \Omega$ resistor is:}
\text{Answer E}
\text{In Figure 6, find the equivalent resistance between points a and b}
A) 7.0\hspace{1mm} \Omega\\
B) 10 \hspace{1mm}\Omega\\
C)45 \hspace{1mm}\Omega\\
D) 40 \hspace{1mm}\Omega \\
E) 17 \hspace{1mm}\Omega


2.0 \text{ }\Omega
6.0\text{ }\Omega




4.0 \text{ }\Omega
10\text{ }\Omega
3.0\text{ }\Omega
12\text{ }\Omega
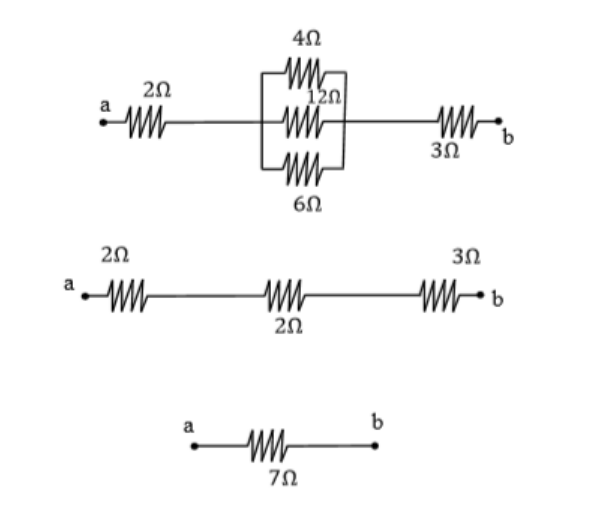
\text{Answer:}
\text{where did go the $10$ $\Omega$ resistor?}

r_1=10\hspace{1mm}\Omega
r_2=0\hspace{1mm}\Omega
\frac{1}{r_\text{eq}}=\frac{1}{r_1}+\frac{1}{r_2}=\frac{1}{r_1}+\frac{1}{0}=\frac{1}{r_1}+\infty=\infty
r_\text{eq}=\frac{1}{\infty}=0
\text{the equivalent resistance =0, }\\
\text{which means it is just a wire!}
\text{In Figure 6, find the equivalent resistance between points a and b}


2.0 \text{ }\Omega
6.0\text{ }\Omega




4.0 \text{ }\Omega
10\text{ }\Omega
3.0\text{ }\Omega
12\text{ }\Omega
\text{For the circuit given in FIGURE 5, if the current through one of the $6.00 \Omega$ is $0.500 \mathrm{~A}$ find }
\text{the current through the $4.00 \Omega$ resistor.}




2.00 \text{ }\Omega
6.00 \text{ }\Omega
6.00 \text{ }\Omega
9.50 \text{ }V
0.50\text{ } A

6.00 \text{ V}
4.00 \text{ }\Omega
i_2
\text{For the circuit given in FIGURE 5, if the current through one of the $6.00 \Omega$ is $0.500 \mathrm{~A}$ find }
\text{the current through the $4.00 \Omega$ resistor.}
\text{since we have the value of $i_1$,}
\text{one loop will be sufficient}
1)\text{choose the directions of $i_1$ and $i_2$}
2)\text{choose the direction of the loop (counter-clockwise)}
3)\text{draw the arrows for the potential increase}
a)\text{at emf: \textcolor{green}{towards the +}}
b)\text{at resistors: \textcolor{green}{opposit to current}}
4)\text{the sum of potentials =0: if with the chosen direction it is + if against it is $-$}
\xi-R_2i_2+R_1i_1=0
\Rightarrow
i_2=\frac{\xi+R_1i_1}{R_2}=\frac{6+6\times0.5}{4}=2.25 A



2.00 \text{ }\Omega
6.00 \text{ }\Omega
6.00 \text{ }\Omega
9.50 \text{ }V
i_1=0.50\text{ } A

6.00 \text{ V}
4.00 \text{ }\Omega
i_2
\circlearrowleft
\xi
R_1 i_1
R_2 i_2
\text{An emf source with $\mathscr{E}=100 \mathrm{~V}$, a resistor with resistance $R=90.0 \Omega$, and a capacitor with}
\text{capacitance $C=5.00 \mu \mathrm{F}$ are connected in series. As the capacitor charges, what is the charge}
\text{on the capacitor when the current in the resistor is $0.800 \mathrm{~A}$ ?}

\text{An emf source with $\mathscr{E}=100 \mathrm{~V}$, a resistor with resistance $R=90.0 \Omega$, and a capacitor with}
\text{capacitance $C=5.00 \mu \mathrm{F}$ are connected in series. As the capacitor charges, what is the charge}
\text{on the capacitor when the current in the resistor is $0.800 \mathrm{~A}$ ?}
\begin{aligned}
& q=\mathrm{q}_m\left(1-e^{-\frac{t}{\tau}}\right)=\mathrm{q}_m-\mathrm{q}_m e^{-\frac{t}{\tau}} \\
& \begin{aligned}
i= & \frac{q_m}{\tau} e^{-\frac{t}{\tau}} \Rightarrow e^{-\frac{t}{\tau}}=\frac{i \tau}{q_m} \\
\Rightarrow q & =q_m\left(1-\frac{i \tau}{q_m}\right)=q_m-i \tau \\
& =\mathrm{C} \varepsilon-i \mathrm{RC}=\mathrm{C}(\varepsilon-i \mathrm{R}) \\
& =5 \times(100-72)=140 \mu C
\end{aligned}
\end{aligned}
\text{Answer D}
\text{A $1.0 \mu \mathrm{F}$ capacitor with an initial stored energy of 0.50 J is discharged through 1.0 $\mathrm{M} \Omega$ resistor.}
\text{Find the charge on the capacitor at $\mathrm{t}=0.40 \mathrm{~s}$.}
\text{A) $6.7 \times 10^{-4} \mathrm{C}$}
\text{B) $3.7 \times 10^{-4} \mathrm{C}$}
\text{C) $1.3 \times 10^{-4} \mathrm{C}$}
\text{D) $9.4 \times 10^{-4} \mathrm{C}$}
\text{E) $7.3 \times 10^{-4} \mathrm{C}$}
\begin{aligned}
& \mathrm{Q}=\mathrm{Q}_0 \mathrm{e}^{-\mathrm{t} / \mathrm{RC}} \\
& \mathrm{U}_0=\frac{1}{2} \frac{\mathrm{Q}_0{ }^2}{\mathrm{C}} \Rightarrow \mathrm{Q}_0=\sqrt{2 \mathrm{CU}_0} \\
& \mathrm{Q}=\sqrt{2 \mathrm{CU}_0} \mathrm{e}^{-\mathrm{t} / \mathrm{RC}}=6.7 \times 10^{-4} \mathrm{C}
\end{aligned}
\text{A $1.0 \mu \mathrm{F}$ capacitor with an initial stored energy of 0.50 J is discharged through 1.0 $\mathrm{M} \Omega$ resistor.}
\text{Find the charge on the capacitor at $\mathrm{t}=0.40 \mathrm{~s}$.}
\text{A) $6.7 \times 10^{-4} \mathrm{C}$}
\text{B) $3.7 \times 10^{-4} \mathrm{C}$}
\text{C) $1.3 \times 10^{-4} \mathrm{C}$}
\text{D) $9.4 \times 10^{-4} \mathrm{C}$}
\text{E) $7.3 \times 10^{-4} \mathrm{C}$}
\text{For a capacitor which is being charged, which one of the following statements is FALSE?}
\text{A) Initially ( at t=0) the capacitor acts like a broken wire in the circuit.}
\text{B) Initially ( at t=0) the capacitor acts like ordinary conducting wire.}
\text{C) After a long time the potential across the capacitor is equal to the emf of the battery.}
\text{D) Initially the current through the capacitor is maximum.}
\text{E) Initially ( at t=0) the potential difference across the capacitor is equal to zero.}
\text{For a capacitor which is being charged, which one of the following statements is FALSE?}
\text{A) Initially ( at t=0) the capacitor acts like a broken wire in the circuit.}
\text{B) Initially ( at t=0) the capacitor acts like ordinary conducting wire.}
\text{C) After a long time the potential across the capacitor is equal to the emf of the battery.}
\text{D) Initially the current through the capacitor is maximum.}
\text{E) Initially ( at t=0) the potential difference across the capacitor is equal to zero.}
\text{Additional problems:}


R_1

\cdot
\cdot
\cdot
R_2
R_3
S
\begin{aligned}&\text{A)2.3A}\\&\text{B)1.6A}\\&\text{C)28mA}\\&\text{D)68mA}\\&\text{E)97mA}\end{aligned}
\begin{aligned}
&\text{In the circuit shown in Figure 8, resistances $R_{1}=15\hspace{1mm}\Omega,R_{2}=20\hspace{1mm}\Omega$, and $R_{3}=60\hspace{1mm}\Omega.$ When }\\
&\text{switch S is open, the current in $R_1$ is 2.0 A. What is the current in $R_1$ when the switch is closed?}
\end{aligned}
C
R_1
R_2
\xi
s
A) 1.50 \hspace{1mm}mA\\
B) 0.75 \hspace{1mm}mA\\
C) 3.00 \hspace{1mm}mA\\
D) 4.10\hspace{1mm}mA\\
\hspace{-6mm} E) Zero
\begin{aligned}
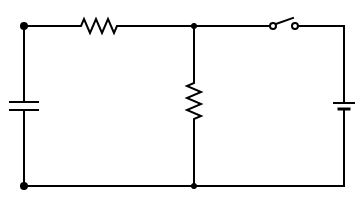
&\text{In the circuit shown in Figure 9, $R_1=R_2=3.0\hspace{1mm}k\Omega$, $C=12\hspace{1mm}\mu F$ and emf $\xi=4.5 \hspace{1mm}V$}\\
& \text{Switch S is closed at t=0. After a long time, what is the current through resistor $R_2$}?
\end{aligned}

\text{Challenge}
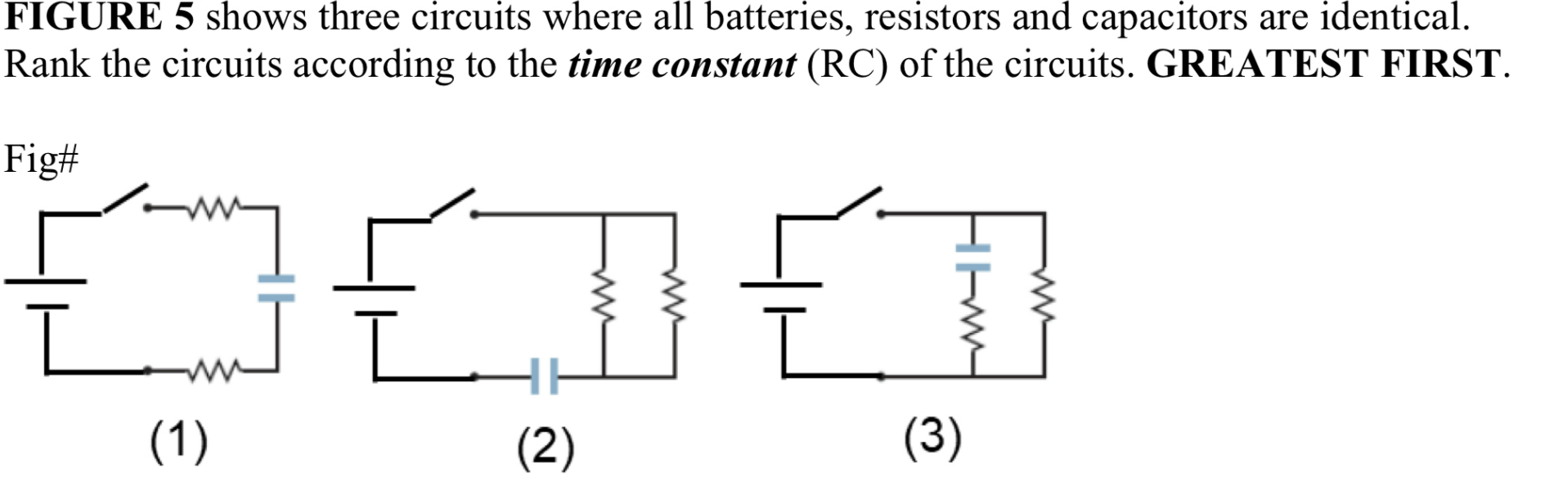
\text{Answer: 1, 3, 2}
\text{A segment of a circuit diagram is shown in Figure 6. At a particular instant, if $R=2.0 \mathrm{k} \Omega$,}
\text{$C=4.0 \mathrm{mF}, \varepsilon=8.0 \mathrm{~V}, Q=20 \mathrm{mC}$, and $i=3.0 \mathrm{~mA}$, what is the potential difference $V_a-V_b$ ?}
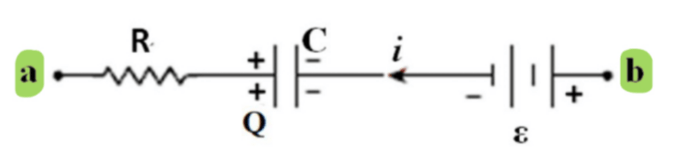
\text{A segment of a circuit diagram is shown in Figure 6. At a particular instant, if $R=2.0 \mathrm{k} \Omega$,}
\text{$C=4.0 \mathrm{mF}, \varepsilon=8.0 \mathrm{~V}, Q=20 \mathrm{mC}$, and $i=3.0 \mathrm{~mA}$, what is the potential difference $V_a-V_b$ ?}
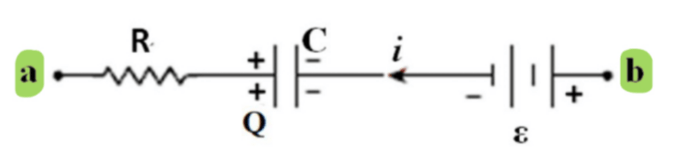
\text{Answer A}

Chapter 27
By smstry
Chapter 27
- 591



