\text{Chapter 7}
\text{Chapter 7}
\text{Chapter 7}
\text{Chapter 7}
\textit{Dr. Adel Abbout}
\text{Kinetic energy}
K=\frac{1}{2}m v^2
\text{Work by a constant force}
W=\vec{F}.\vec{d}
\text{Work-Kinetic energy theorem}
\Delta K=W
\text{(Net work done on the object)}
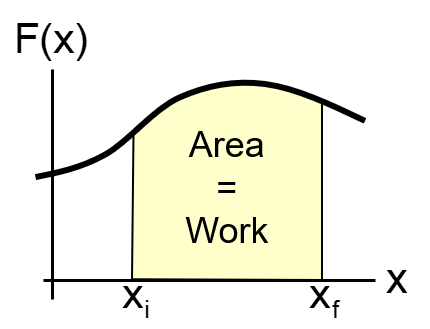
W=\int_{x_i}^{x_f} F(x) d x
\text{Work done by \textcolor{red}{variable}} \\\text{one dimentional force}
W=\frac{1}{2} k x_i^2-\frac{1}{2} k x_f^2
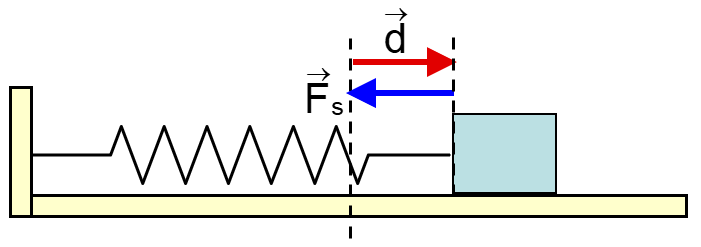
\text{Work done by spring force}
F=-k x
x
\text{Hook's law}
\text{Average power}
P_{\text {avg }}=\frac{W}{\Delta t}
\text{Power}
P=\vec{F}.\vec{v}
\text{area under the curve}
\text{A) $0.44 \mathrm{~m}$}\\
\text{B) $0.39 \mathrm{~m}$}\\
\text{C) $0.23 \mathrm{~m}$}\\
\text{D) $0.13 \mathrm{~m}$}\\
\text{E) $0.56 \mathrm{~m}$}
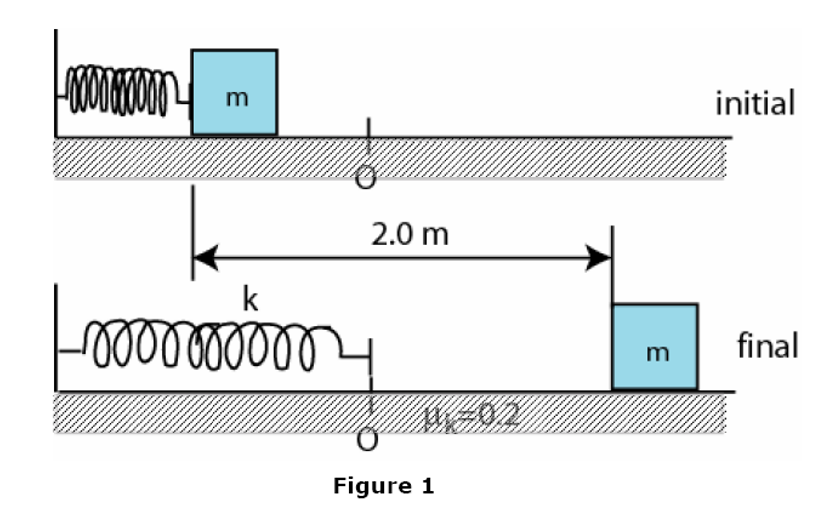
\text{A $3.0 \mathrm{~kg}$ block is released from a compressed spring $(\mathrm{k}=120 \mathrm{~N} / \mathrm{m})$. It travels over a horizontal}
\text{ surface $(\mathrm{\mu_k}=0.20)$ for a distance of $2.0 \mathrm{~m}$ before coming to rest, Fig 1. }
\text{How far was the spring compressed before being released?}
\text{A $3.0 \mathrm{~kg}$ block is released from a compressed spring $(\mathrm{k}=120 \mathrm{~N} / \mathrm{m})$. It travels over a horizontal}
\text{ surface $(\mathrm{\mu_k}=0.20)$ for a distance of $2.0 \mathrm{~m}$ before coming to rest, Fig 1. }
\text{How far was the spring compressed before being released?}

\Delta K=W(\vec{F}_\text{net})=W(m\vec{g})+W(\vec{F}_N)+W(\vec{f})+W(\vec{F}_s)
K_\text{f}=K_\text{i}-\mu_k m g d+\frac{1}{2}k x_\text{i}^2
W(m\vec{g})=W(\vec{F}_N)=0
W(\vec{f})=\vec{f}.\vec{d}=-f d=-\mu_k mg d
\displaystyle W(\vec{F}_s)=\frac{1}{2}k x_\text{i}^2-\frac{1}{2}k x_\text{f}^2=\frac{1}{2}k x_\text{i}^2
(x_\text{f}=0)
\text{The block was released without speed $(K_\text{i}=0)$ and stops at the end $(K_\text{f}=0)$}
\displaystyle x_\text{i}=\sqrt{\frac{2\mu_k m g d}{k}}
\displaystyle x_\text{i}=\sqrt{\frac{2 \times0.2\times 3.0 \times9.8\times 2.0}{120}}=0.44 \text{ m}
\text{Answer: A) 0.44 \text{m}}
\vec{F}_s
\vec{f}
m\vec{g}
(F_N=mg)
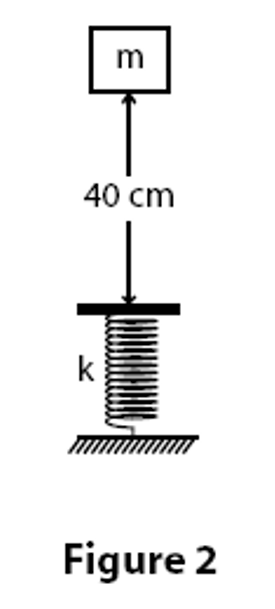
\text{A $3.00 \mathrm{~kg}$ block is dropped from a height of $40 \mathrm{~cm}$ onto a spring of spring constant $\mathrm{k}$ (see Fig 2). }
\text{If the maximum distance the spring is compressed $=0.130 \mathrm{~m}$, find $\mathrm{k}$.}
\text{A) $490 \mathrm{~N} / \mathrm{m}$}\\
\text{B) $980 \mathrm{~N} / \mathrm{m}$}\\
\text{C) $1840 \mathrm{~N} / \mathrm{m}$}\\
\text{D) $1250 \mathrm{~N} / \mathrm{m}$}\\
\text{E) $2800 \mathrm{~N} / \mathrm{m}$}
\text{A $3.00 \mathrm{~kg}$ block is dropped from a height of $40 \mathrm{~cm}$ onto a spring of spring constant $\mathrm{k}$ (see Fig 2). }
\text{If the maximum distance the spring is compressed $=0.130 \mathrm{~m}$, find $\mathrm{k}$.}

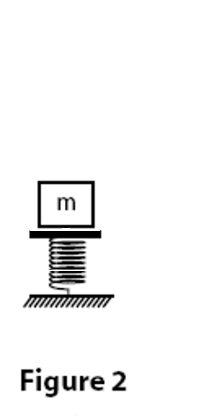
d
x
\Delta K=W(m\vec{g})+W(\vec{F_s})
\text{Be careful, $\vec{F}_g$ works even when the spring is being compressed}
\displaystyle \Delta K=m g (d+x)+(\frac{1}{2}kx^2_\text{i}-\frac{1}{2}kx^2)
=
0
\text{Block was at rest \textcolor{red}{$K_\text{i}=0$.} }
\text{At maximum compressin, the block stops momentarilty. \textcolor{red}{$K_\text{f}=0$}}
\displaystyle 0=m g (d+x)-\frac{1}{2}kx^2
\displaystyle k=\frac{2m g (d+x)}{x^2}=\frac{2\times3.0 \times 9.8\times (0.40+.130)}{0.130^2}=1844\text{ N/m}
\text{Answer C)}
\text{(A more difficult version of this problem is in the next slide)}
\text{Warning}
\text{The relation}
\displaystyle \text{$W(\vec{F}_s)=\frac{1}{2}k x_\text{i}^2-\frac{1}{2}k x_\text{f}^2$}
\text{ the origin of your axis is the position where the spring is neither stretched nor compressed}
\text{is correct only if:}
x
x_\text{f}
\text{Correct}
\text{Wrong}
\text{Wrong}
x
x_\text{f}
l_0
0

0
l_0

x
x_\text{f}
0
l_0

\text{A $16 \mathrm{~kg}$ crate falls from rest from a height of $1.0 \mathrm{~m}$ onto a spring scale with a spring constant }
\text{of $2.74 \times 10^3 \mathrm{~N} / \mathrm{m}$. Find the maximum distance the spring is compressed.}
\text{A) $40 \mathrm{~cm}$}\\
\text{B) $2.0 \mathrm{~cm}$}\\
\text{C) $60 \mathrm{~cm}$}\\
\text{D) $7.0 \mathrm{~cm}$}\\
\text{E) $5.0 \mathrm{~cm}$}
1.0 \text{ m}


d
x
\displaystyle 0=m g (d+x)-\frac{1}{2}kx^2
\text{A $16 \mathrm{~kg}$ crate falls from rest from a height of $1.0 \mathrm{~m}$ onto a spring scale with a spring constant }
\text{of $2.74 \times 10^3 \mathrm{~N} / \mathrm{m}$. Find the maximum distance the spring is compressed.}
kx^2-2mgx -2m g d=0
\Delta K=W(m\vec{g})+W(\vec{F_s})
\text{Be careful, $\vec{F}_g$ works even when the spring is being compressed}
\displaystyle \Delta K=m g (d+x)+(\frac{1}{2}kx^2_\text{i}-\frac{1}{2}kx^2)
\text{Block was at rest \textcolor{red}{$K_\text{i}=0$.} }
\text{At maximum compressin, the block stops momentarilty. \textcolor{red}{$K_\text{f}=0$}}
\text{During the exam, you can solve it numerically using your calculator.}
2740 x^2-313.6x-313.6=0
x=0.40 \text{ m}\text{ or } x=-0.29 \text{ m}
\Rightarrow
\text{Answer A)}
1.0 \text{ m}
\text{the solusion is }x=40 \text{ cm}


d
x
\text{A $16 \mathrm{~kg}$ crate falls from rest from a height of $1.0 \mathrm{~m}$ onto a spring scale with a spring constant }
\text{of $2.74 \times 10^3 \mathrm{~N} / \mathrm{m}$. Find the maximum distance the spring is compressed.}
kx^2-2mgx -2m g d=0
\text{The expression of the solution can be found this way:}
\displaystyle x=\frac{2mg\pm\sqrt{(2mg)^2+8k mgd}}{2k}
\displaystyle x=\frac{mg\pm\sqrt{(mg)^2+2k mgd}}{k}
\Delta=(2mg)^2+8k mgd
1.0 \text{ m}
\text{At time $t=0$ a single force $\mathbf{F}$ acts on a $2.0 \mathrm{~kg}$ particle and changes its velocity from }
\text{$\mathbf{v}_{\mathbf{i}}=(4.0 \mathbf{i}-3.0 \mathbf{j}) \mathrm{m} / \mathrm{s}$ at $\mathrm{t}=0$ to $\mathbf{v}_{\mathrm{f}}=(4.0 \mathbf{i}+3.0 \mathbf{j}) \mathrm{m} / \mathrm{s}$ at $\mathrm{t}=$ $3.0 \mathrm{~s}$.}
\text{During this time the work done by $\mathbf{F}$ on the particle is:}
\text{A) $2.0 \mathrm{~J}$}\\
\text{B) $6.0 \mathrm{~J}$}\\
\hspace{-5mm}\text{C) 0}\\
\text{D) $50 \mathrm{~J}$}\\
\text{E) $10 \mathrm{~J}$}
\text{At time $t=0$ a single force $\mathbf{F}$ acts on a $2.0 \mathrm{~kg}$ particle and changes its velocity from }
\text{$\mathbf{v}_{\mathbf{i}}=(4.0 \mathbf{i}-3.0 \mathbf{j}) \mathrm{m} / \mathrm{s}$ at $\mathrm{t}=0$ to $\mathbf{v}_{\mathrm{f}}=(4.0 \mathbf{i}+3.0 \mathbf{j}) \mathrm{m} / \mathrm{s}$ at $\mathrm{t}=$ $3.0 \mathrm{~s}$.}
\text{During this time the work done by $\mathbf{F}$ on the particle is:}
\text{A) $2.0 \mathrm{~J}$}\\
\text{B) $6.0 \mathrm{~J}$}\\
\hspace{-5mm}\text{C) 0}\\
\text{D) $50 \mathrm{~J}$}\\
\text{E) $10 \mathrm{~J}$}
\Delta K=W(\bf{F})
\displaystyle \Delta K=K_\text{f}-K_\text{i}=\frac{1}{2}m v_\text{f}^2-\frac{1}{2}m v_\text{i}^2
\displaystyle \Delta K=K_\text{f}-K_\text{i}=\frac{1}{2}m (4^2+3^2)-\frac{1}{2}m (4^2+(-3)^2)=0
\Delta K=W(\bf{F})=0
\text{Answer C)}
\text{A projectile is fired from the top of a $40 \mathrm{~m}$ high building with a speed of 20 $\mathrm{m} / \mathrm{s}$.}
\text{What will be its speed when it strikes the ground?}
\text{A) $82 \mathrm{~m} / \mathrm{s}$}\\
\text{B) $10 \mathrm{~m} / \mathrm{s}$}\\
\text{C) $34 \mathrm{~m} / \mathrm{s}$}\\
\text{D) $16 \mathrm{~m} / \mathrm{s}$}\\
\text{E) $50 \mathrm{~m} /\mathrm{s}$}
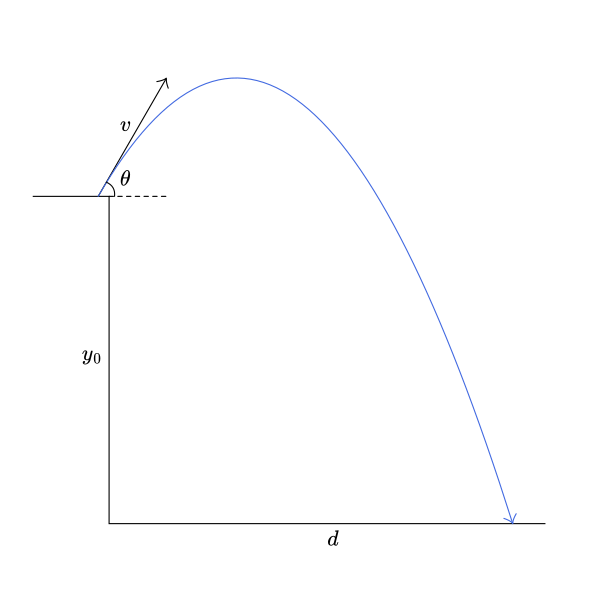
\text{Let us consider a general case where the angle $\theta$ is not known.}
\text{A projectile is fired from the top of a $40 \mathrm{~m}$ high building with a speed of 20 $\mathrm{m} / \mathrm{s}$.}
\text{What will be its speed when it strikes the ground?}

\text{Let us consider a general case where the angle $\theta$ is not known.}
\text{The work of a conservative force, does not depend on the path we take.}
\text{$m\vec{g}$}
\text{The work along the \textcolor{orange}{orange} path is easiest to calculate}
W(m\vec{g})=mgy+mgd\cos 90^0=mgy
\Delta K=W \Rightarrow K_\text{f}=K_\text{i}+mgy
v_\text{f}^2=v_\text{i}^2+2gy\Rightarrow
v_\text{f}=\sqrt{v_\text{i}^2+2gy}=\sqrt{20^2+2\times 9.8\times 40}
v_\text{f}\approx 34 \text{ m/s}
\text{Answer C)}
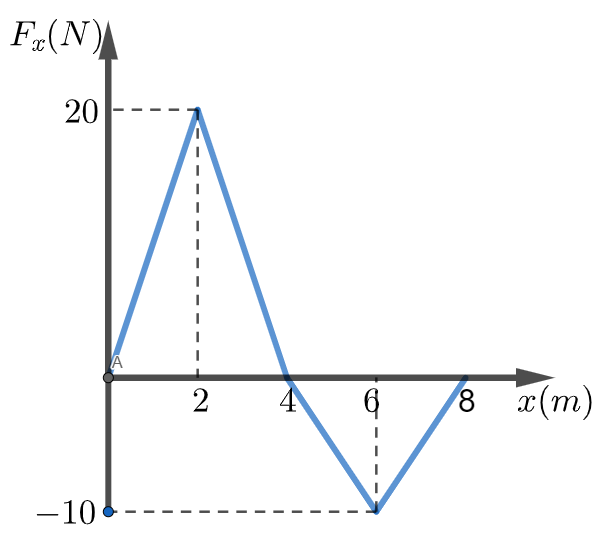
\text{Fig. 1 gives the only force $F_x$ that can act on a particle. If the particle has a kinetic energy}
\text{ of $10 \mathrm{~J}$ at $\mathrm{x}=0$, find the kinetic energy of the particle when it is at $x=8.0 \mathrm{~m}$.}
\hspace{-2mm}\text{A) $0 \mathrm{~J}$}\\
\text{B) $20 \mathrm{~J}$}\\
\text{C) $30 \mathrm{~J}$}\\
\text{D) $60 \mathrm{~J}$}\\
\text{E) $10 \mathrm{~J}$}
\text{Fig. 1 gives the only force $F_x$ that can act on a particle. If the particle has a kinetic energy}
\text{ of $10 \mathrm{~J}$ at $\mathrm{x}=0$, find the kinetic energy of the particle when it is at $x=8.0 \mathrm{~m}$.}

W(F_x)=\text{Area under the curve}
\displaystyle W(F_x)=\frac{1}{2}(20 N\times 4 m)-\frac{1}{2}(10 N\times 4 m)=20J
\text{Answer C)}
\Delta K=W(F_s)\Rightarrow K_\text{f}=K_\text{i}+W(F_s)=10+20=30J
\begin{align*}
&\text{Figure 1 shows a graph of the acceleration versus the displacement of a particle moving in } &\\
&\text{one dimension. The particle is at rest at } x=0.&\\
&\text{What is the coordinate } x \ \text{at which the particle has the maximum kinetic energy?} &\\
&\text{(Vertical axis label: } a_x \ (\mathrm{m/s^2})\text{; horizontal axis label: } x \ (\mathrm{m})\text{; see Figure 1.)}&\\
\\
&\text{A) }3 \qquad&\\
&\text{B) }1 \qquad&\\
&\text{C) }5 \qquad&\\
&\text{D) }7 \qquad&\\
&\text{E) }8&
\end{align*}
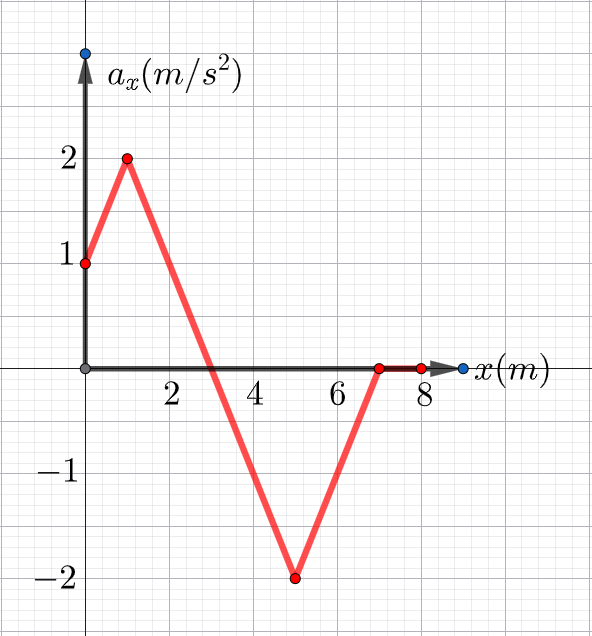
\begin{align*}
&\text{Figure 1 shows a graph of the acceleration versus the displacement of a particle moving in } &\\
&\text{one dimension. The particle is at rest at } x=0.&\\
&\text{What is the coordinate } x \ \text{at which the particle has the maximum kinetic energy?} &\\
&\text{(Vertical axis label: } a_x \ (\mathrm{m/s^2})\text{; horizontal axis label: } x \ (\mathrm{m})\text{; see Figure 1.)}&\\
\end{align*}
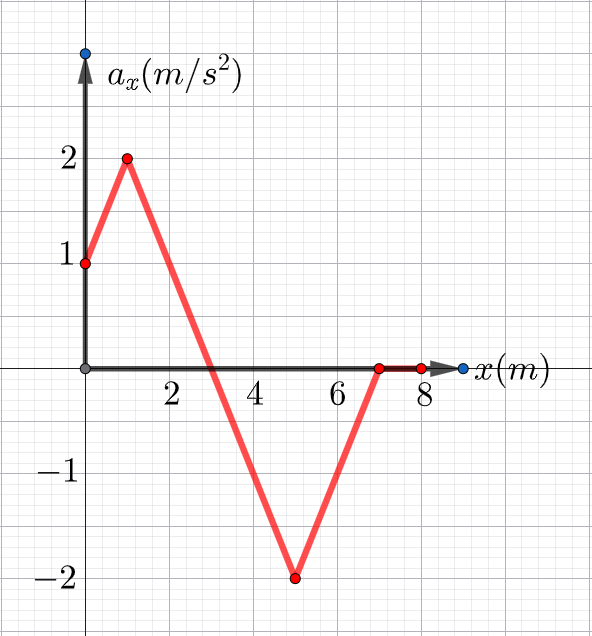
a_x=\frac{F_x}{m}
\int a_x dx=\frac{1}{m}\int F_x dx= \frac{W}{m}
\text{The area under the curve of $a_x$ vs $x$ }\\
\text{represents the work per unit $m$}
W=\Delta K=\frac{1}{2}m v^2-\underbrace{\frac{1}{2}m v_i^2}_{=0}=\frac{1}{2}m v^2
\text{kinetic energy is maximum where W or (W/m) is maximum}
\text{A $200 \mathrm{~kg}$ box is pulled along a horizontal surface by an engine. The coefficient of friction}
\text{ between the box and the surface is 0.400. }
\text{Answer C)}
\text{The power the engine delivers to move the box at constant speed of $5.00 \mathrm{~m} / \mathrm{s}$ is:}
\text{A) $3920 \mathrm{~W}$}\\
\text{B) $1960 \mathrm{~W}$}\\
\hspace{-2mm}\text{C) $980 \mathrm{~W}$}\\
\hspace{-2.2mm}\text{D) $490 \mathrm{~W}$}\\
\hspace{-5mm}\text{E) $0 \mathrm{~W}$}
\vec{T}
\vec{f}
m
\text{A $200 \mathrm{~kg}$ box is pulled along a horizontal surface by an engine. The coefficient of friction}
\text{ between the box and the surface is 0.400. }
\text{Answer A)}
\text{The power the engine delivers to move the box at constant speed of $5.00 \mathrm{~m} / \mathrm{s}$ is:}
\vec{T}
\vec{f}
m
\text{constant speed means that $\vec{a}=0$}
\text{we deduce that }T=f
P(T)=\vec{T}.\vec{v}=T v=\mu_k mg v
=0.400 \times200 \times 9.8\times 5.00
=0.400 \times200 \times 9.8\times 5.00
=3920\text{ W}
{m\vec{g}}
\vec{N}
\text{A helicopter lifts an $80 \mathrm{~kg}$ man vertically from the ground by means of a cable. The upward }
\text{ acceleration of the man is $2.0 \mathrm{~m} / \mathrm{s}^2$. Find the rate at which the work is being done on the man}
\text{by the tension of the cable when the speed of the man is $1.5 \mathrm{~m} / \mathrm{s}$.}
\text{A) $1.8 \times 10^3 \mathrm{~W}$}\\
\text{B) $1.1 \times 10^3 \mathrm{~W}$}\\
\text{C) $1.2 \times 10^4 \mathrm{~W}$}\\
\text{D) $1.4 \times 10^3 \mathrm{~W}$}\\
\text{E) $2.5 \times 10^4 \mathrm{~W}$}
\text{A helicopter lifts an $80 \mathrm{~kg}$ man vertically from the ground by means of a cable. The upward }
\text{ acceleration of the man is $2.0 \mathrm{~m} / \mathrm{s}^2$. Find the rate at which the work is being done on the man}
\text{Answer D)}
\text{by the tension of the cable when the speed of the man is $1.5 \mathrm{~m} / \mathrm{s}$.}
\vec{T}
m\vec{g}
\vec{a}
m\vec{g}+\vec{T}=m\vec{a}
\text{projection on the y-axis:}
-m{g}+{T}=m{a} \Rightarrow
{T}=m{a}+m{g}
{T}=80 \times (2+9.8)=944 \text{ N}
\displaystyle P=\frac{dW(\vec{T})}{dt}=\vec{T}.\vec{v}=T v=944\times 1.5=1416 \text{ W}
\text{A force $\mathbf{F}=(3.00 \mathbf{i}+7.00 \mathbf{j}) \mathrm{N}$ acts on a $2.00 \mathrm{~kg}$ object that moves from an initial position}
\text{$\mathbf{r}_1=(3.00 \mathbf{i}-2.00 \mathbf{j}) \mathrm{m}$ to a final position $\mathbf{r}_2=(5.00 \mathbf{i}+4.00 \mathbf{j}) \mathrm{m}$ in $4.00 \mathrm{~s}$.}
\text{What is the average power due to the force during that time interval?}
\hspace{-2mm}\text{A) $8.0 \mathrm{~W}$}\\
\text{B) $7.00 \mathrm{~W}$}\\
\hspace{2 mm}\text{C) $12.00 \mathrm{~W}$}\\
\text{D) $6.00 \mathrm{~W}$}\\
\text{E) $16.0 \mathrm{~W}$}
\text{A force $\mathbf{F}=(3.00 \mathbf{i}+7.00 \mathbf{j}) \mathrm{N}$ acts on a $2.00 \mathrm{~kg}$ object that moves from an initial position}
\text{$\mathbf{r}_1=(3.00 \mathbf{i}-2.00 \mathbf{j}) \mathrm{m}$ to a final position $\mathbf{r}_2=(5.00 \mathbf{i}+4.00 \mathbf{j}) \mathrm{m}$ in $4.00 \mathrm{~s}$.}
\text{What is the average power due to the force during that time interval?}
\displaystyle \vec{V}_\text{avg}=\frac{\vec{r}_2-\vec{r}_1}{\Delta t}=\frac{2.00 {\bf{ i}}+6.00 \bf{ j}}{4.00}=0.50 {\bf i}+1.50{\bf j}
\text{$P_\text{avg}=\vec{F}.\vec{V}_\text{avg}$}=3.00\times0.50+7.00\times1.50=12.00 \text{ W}
\text{Answer C)}
\begin{align*}
&\text{What is the work done by the force } \vec{F}=(2.0\,\hat{\imath}+4.0\,\hat{\jmath}+9.0\,\hat{k})~\mathrm{N}\text{ that acts on a }3.0~\mathrm{kg}\\
&\text{object and moves from an initial position }\vec{r}_1=(-4.1\,\hat{\imath}+3.3\,\hat{\jmath}+5.2\,\hat{k})~\mathrm{m}\text{to a final position }&\\
&\vec{r}_2=(2.7\,\hat{\imath}-2.9\,\hat{\jmath}+5.5\,\hat{k})~\mathrm{m}\,?&\\
\\
&\text{A) }-8.5~\mathrm{J}\qquad&\\
&\text{B) }-12~\mathrm{J}\qquad&\\
&\text{C) }+5.2~\mathrm{J}\qquad&\\
&\text{D) }+12~\mathrm{J}\qquad&\\
&\text{E) }+4.7~\mathrm{J}&
\end{align*}
\begin{align*}
&\text{What is the work done by the force } \vec{F}=(2.0\,\hat{\imath}+4.0\,\hat{\jmath}+9.0\,\hat{k})~\mathrm{N}\text{that acts on a }3.0~\mathrm{kg}\\
&\text{object and moves from an initial position }\vec{r}_1=(-4.1\,\hat{\imath}+3.3\,\hat{\jmath}+5.2\,\hat{k})~\mathrm{m}\text{to a final position }&\\
&\vec{r}_2=(2.7\,\hat{\imath}-2.9\,\hat{\jmath}+5.5\,\hat{k})~\mathrm{m}\,?&\\
\\
&\text{A) }-8.5~\mathrm{J}\qquad&\\
&\text{B) }-12~\mathrm{J}\qquad&\\
&\text{C) }+5.2~\mathrm{J}\qquad&\\
&\text{D) }+12~\mathrm{J}\qquad&\\
&\text{E) }+4.7~\mathrm{J}&
\end{align*}
W=\vec{F}.\vec{d}=2\times 6.8+4\times (-6.2)+9\times0.3=-8.5 \mathrm{~J}
\vec{d}=(\vec{r}_f-\vec{r}_i)=6.8 \hat{\imath}-6.2 \hat{\jmath}+0.3 \,\hat{k}
Chapter 7-Phys101
By smstry
Chapter 7-Phys101
- 333



