\text{Chapter 8}
\text{Chapter 8}
\text{Chapter 8}
\text{Chapter 8}
\textit{Dr. Adel Abbout}
\text{A $2.0 \mathrm{~kg}$ block is thrown upward from the ground. At what height above the ground will }
\text{the gravitational potential energy of the Earth-block system have increased by $490 \mathrm{~J}$ ?}
\text{A) $12 \mathrm{~m}$}\\
\text{B) $50 \mathrm{~m}$}\\
\text{C) $25 \mathrm{~m}$}\\
\text{D) $8.0 \mathrm{~m}$}\\
\text{E) $18 \mathrm{~m}$}
\text{A $2.0 \mathrm{~kg}$ block is thrown upward from the ground. At what height above the ground will }
\text{the gravitational potential energy of the Earth-block system have increased by $490 \mathrm{~J}$ ?}
\text{A) $12 \mathrm{~m}$}\\
\text{B) $50 \mathrm{~m}$}\\
\text{C) $25 \mathrm{~m}$}\\
\text{D) $8.0 \mathrm{~m}$}\\
\text{E) $18 \mathrm{~m}$}
\Delta U=mgy
\text{where }y \text{ is measure from the ground as reference.}
\displaystyle y=\frac{\Delta U}{mg}=\frac{490}{2.0\times 9.8}\approx 25\text{ m}
\text{Answer C)}
\text{An ideal spring with a $20 \mathrm{~N} / \mathrm{m}$ spring constant is compressed by a $10 \mathrm{~N}$ force. The potential }
\text{A) $0.50 \mathrm{~J}$}\\
\text{B) $2.5 \mathrm{~J}$}\\
\text{C) $5.0 \mathrm{~J}$}\\
\text{D) $10 \mathrm{~J}$}\\
\text{E) $200 \mathrm{~J}$}
\text{energy stored in the spring is: }
\text{An ideal spring with a $20 \mathrm{~N} / \mathrm{m}$ spring constant is compressed by a $10 \mathrm{~N}$ force. The potential }
\text{A) $0.50 \mathrm{~J}$}\\
\text{B) $2.5 \mathrm{~J}$}\\
\text{C) $5.0 \mathrm{~J}$}\\
\text{D) $10 \mathrm{~J}$}\\
\text{E) $200 \mathrm{~J}$}
\text{Answer B)}
\text{energy stored in the spring is: }
\displaystyle U=\frac{1}{2}k x_\text{}^2
\text{The elastic potential energy is:}
\text{(When the spring is relaxed, its energy is 0)}
\displaystyle F=k x
\text{(magnitude)}
\displaystyle U=\frac{1}{2}\frac{F^2}{k} =\frac{10^2}{2\times20}=2.5 \text{ J}
\text{A $2.0 \mathrm{~kg}$ object is connected to one end of an unstretched spring which is attached to the ceiling }
\text{A) $0.80 \mathrm{~m}$}\\
\text{B) $0.10 \mathrm{~m}$}\\
\text{C) $0.40 \mathrm{~m}$}\\
\text{D) $0.20 \mathrm{~m}$}\\
\text{E) $0.50 \mathrm{~m}$}
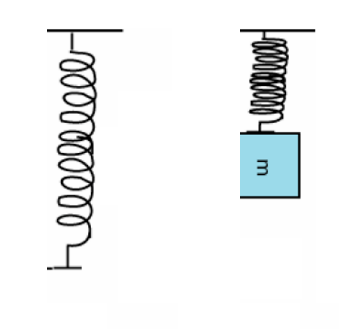
\text{by the other end and then the object is allowed to drop. The spring constant of the spring }
\text{is $196 \mathrm{~N} / \mathrm{m}$. How far does it drop before coming to rest momentarily?}
m
m
\text{reference}
k
\text{(not compressed)}
\text{A $2.0 \mathrm{~kg}$ object is connected to one end of an unstretched spring which is attached to the ceiling }
\text{by the other end and then the object is allowed to drop. The spring constant of the spring }
\text{is $196 \mathrm{~N} / \mathrm{m}$. How far does it drop before coming to rest momentarily?}
\text{We take the same reference for the potential energy and the elastic one.}
\text{To avoid problems, take it at the position }\\
\text{where the spring is not stretched.}
\text{The mechanical energy is conserved:}
K_\text{i}+U_\text{i}=K_\text{f}+U_\text{f}
\displaystyle \frac{1}{2}mv_\text{i}^2+mgy_0+\frac{1}{2} k x_\text{i}^2=\frac{1}{2}mv_\text{f}^2+mgy+\frac{1}{2} k x_\text{f}^2
x_\text{i}=y_0=0
v_\text{i}=v_\text{f}=0
x_\text{f}=y
(\text{reference})
(\text{at rest})
\text{(same distance)}
\displaystyle 0=mgy+\frac{1}{2} k y^2
\displaystyle 0=mgy+\frac{1}{2} k y^2
\displaystyle y=-\frac{2mg}{k}=-\frac{2\times2\times9.8}{196}
\Rightarrow
=-0.20\text{ m}

m
m
\text{reference}
k
y
\text{Answer D)}
\text{(not compressed)}
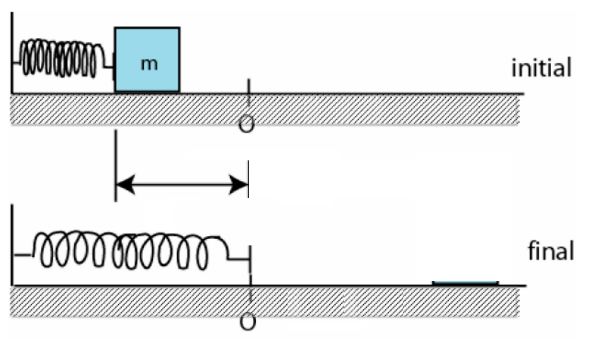
\text{An ideal spring (compressed by $7.00 \mathrm{~cm}$ and initially at rest,) fires a 15.0 $\mathrm{g}$ block horizontally }
\text{across a frictionless table top. The spring has a spring constant of $20.0 \mathrm{~N} / \mathrm{m}$. }
\text{The speed of the block as it leaves the spring is: }
\text{A) $2.56 \mathrm{~m} / \mathrm{s}$}\\
\text{B) $1.90 \mathrm{~m} / \mathrm{s}$}\\
\text{C) $3.64 \mathrm{~m} / \mathrm{s}$}\\
\text{D) $8.12 \mathrm{~m} / \mathrm{s}$}\\
\text{E) $5.25 \mathrm{~m} / \mathrm{s}$}
\text{An ideal spring (compressed by $7.00 \mathrm{~cm}$ and initially at rest,) fires a 15.0 $\mathrm{g}$ block horizontally }
\text{across a frictionless table top. The spring has a spring constant of $20.0 \mathrm{~N} / \mathrm{m}$. }
\text{The speed of the block as it leaves the spring is: }
m
m
7.00 \text{ cm}
\text{The external forces }m\vec{g}\text{ and }\vec{F}_N \text{ are not working}
\text{The mechanical energy of (spring+mass) is \textcolor{red}{conserved}}
K_\text{i}+U_\text{i}=K_\text{f}+U_\text{f}
\displaystyle \frac{1}{2}mv_\text{i}^2+\frac{1}{2} k x_\text{i}^2=\frac{1}{2}mv_\text{f}^2+\frac{1}{2} k x_\text{f}^2
v_\text{i}=0
x_\text{f}=0
(\text{at rest})
\text{(not stretched)}
\text{We have }
\text{ and }
\displaystyle \frac{1}{2} k x_\text{i}^2=\frac{1}{2}mv_\text{f}^2
\displaystyle v=x_\text{i}\sqrt{\frac{k}{m}}
\displaystyle v=0.07\times\sqrt{\frac{20}{15 \times 10^{-3}}}\approx2.56\text{ m/s}
\text{Answer A)}
\text{(kinetic and elastic energies) }
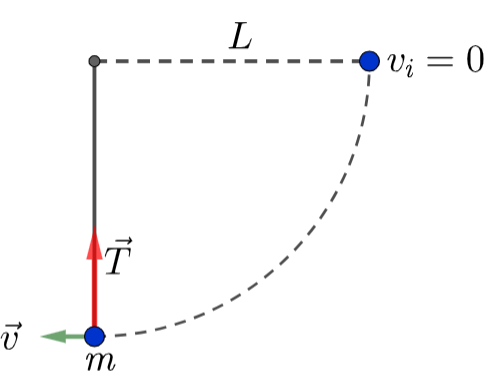
\text{An object of mass $m$, attached to a light cord of length $L$, is held horizontally from a fixed}
\text{ support as shown in Fig 1 . The object is then released from rest.}
\text{ What is the tension force in the cord when the object is at the lowest point of its swing?}
\text{A) $2 \mathrm{ mg}$}\\
\hspace{-2mm}\text{B) $\mathrm{ mg}$}\\
\text{C) $3 \mathrm{ mg}$}\\
\hspace{2mm}\text{D) $\mathrm{ mg} / 2$}\\
\text{E) $\mathrm{ mgL}$}
\text{An object of mass $m$, attached to a light cord of length $L$, is held horizontally from a fixed}
\text{ support as shown in Fig 1 . The object is then released from rest.}
\text{ What is the tension force in the cord when the object is at the lowest point of its swing?}

\Delta E_{mec}=W(\vec{T})
\text{since }\vec{T} \text{ is continously perpendicular to the path,}\\ \text{ its work is therefore }0
\text{The mechanical energy is therefore \textcolor{red}{conserved}}
K_\text{i}+U_\text{i}=K_\text{f}+U_\text{f}
\displaystyle \frac{1}{2}mv_\text{i}^2+mgy=\frac{1}{2}mv_\text{f}^2
\text{The reference for the potential energy is taken at the lowes point}
y=L
v_\text{i}=0
\text{ and }
\Rightarrow
\displaystyle v_\text{f}=\sqrt{2gL}
\text{(system is earth+mass)}
\text{at the lowest point, we have}
m\vec{g}+\vec{T}=m\vec{a}
\text{By projecting on the radial axis, we get where the centripetal acceleration:}
\displaystyle -m{g}+{T}=m{a}=m\frac{v^2}{R}
\Rightarrow
\displaystyle {T}=mg+m\frac{v^2}{R}=mg+2mgL/L=3mg
\text{Answer C)}
\displaystyle {T}=3mg
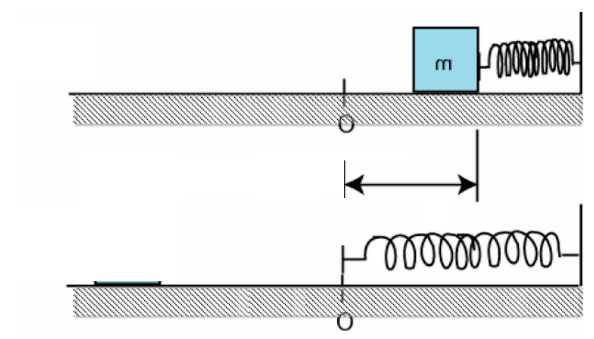
\text{A block of mass $2.0 \mathrm{~kg}$ is initially moving to the right on a horizontal frictionless surface at }
\text{ a speed $5.0 \mathrm{~m} / \mathrm{s}$. It then compresses a spring of spring constant $100 \mathrm{~N} / \mathrm{m}$.}
\text{ At the instant when the kinetic energy of the block is equal to the potential energy of the spring,}
\text{ the spring is compressed a distance of:}
\text{A) $0.25 \mathrm{~m}$}\\
\text{B) $0.50 \mathrm{~m}$}\\
\hspace{-2mm}\text{C) $1.0 \mathrm{~m}$}\\
\text{D) $0.75 \mathrm{~m}$}\\
\text{E) $0.10 \mathrm{~m}$}
\text{A block of mass $2.0 \mathrm{~kg}$ is initially moving to the right on a horizontal frictionless surface at }
\text{ a speed $5.0 \mathrm{~m} / \mathrm{s}$. It then compresses a spring of spring constant $100 \mathrm{~N} / \mathrm{m}$.}
\text{ At the instant when the kinetic energy of the block is equal to the potential energy of the spring,}
\text{ the spring is compressed a distance of:}
{m}
{m}
?
k
\text{initial}
\text{final}
\text{The mechanical energy of the system mass+spring is \textcolor{red}{conserved.}}
K_\text{i}+U_\text{i}=K_\text{f}+U_\text{f}
\text{the initial elastic potential energy is }U_\text{i}=0
K_\text{f}=U_\text{f}\Rightarrow K_\text{f}+U_\text{f}=2U_\text{f}
1
\dots
1
K_\text{i}=2U_\text{f}
\Rightarrow
\displaystyle \frac{1}{2}mv_\text{i}^2= k x_\text{f}^2
\displaystyle x_\text{f}=\sqrt{\frac{m}{2k}}v_\text{i}
\displaystyle x_\text{f}=\sqrt{\frac{2.0}{2\times100}}\times 5.0=0.50 \text{ m}
\displaystyle x_\text{f}=0.50 \text{ m}
\text{Answer B)}
\Rightarrow
\Rightarrow
\Rightarrow
\Rightarrow
\text{A $3.00 \mathrm{~kg}$ block is dropped from a height of $40 \mathrm{~cm}$ onto a spring of spring constant $\mathrm{k}$ (see Fig 2).}
\text{ If the maximum distance the spring is compressed $=0.130 \mathrm{~m}$, find $\mathrm{k}$.}

m
\text{A) $1840 \mathrm{~N} / \mathrm{m}$}\\
\hspace{-2mm}\text{B) $980 \mathrm{~N} / \mathrm{m}$}\\
\hspace{-2mm}\text{C) $490 \mathrm{~N} / \mathrm{m}$}\\
\text{D) $1250 \mathrm{~N} / \mathrm{m}$}\\
\text{E) $2800 \mathrm{~N} / \mathrm{m}$}
\text{A $3.00 \mathrm{~kg}$ block is dropped from a height of $40 \mathrm{~cm}$ onto a spring of spring constant $\mathrm{k}$ (see Fig 2).}
\text{ If the maximum distance the spring is compressed $=0.130 \mathrm{~m}$, find $\mathrm{k}$.}
\text{system=earth+mass+spring}
\text{mechanical energy is \textcolor{red}{conserved}}
K_\text{i}+U_\text{i}^p+U_\text{i}^e=K_\text{f}+U_\text{f}^p+U_\text{f}^e
\displaystyle \frac{1}{2}mv_\text{i}^2+mgy_0+\frac{1}{2} k x_\text{i}^2=\frac{1}{2}mv_\text{f}^2+mgy+\frac{1}{2} k x_\text{f}^2
=
0
=
0
=
0
\displaystyle mg(y_0-y)=\frac{1}{2} k x_\text{f}^2
(\text{the final speed is }0)
y_0-y \text{ is the total distance: }y_0-y=d+x_\text{f}
\displaystyle k=\frac{2mg(d+x_\text{f})}{x_\text{f}^2}
\displaystyle k=\frac{2\times 3.00\times 9.8\times(0.40+0.130)}{0.130^2}\approx1844 \text{ N/m}
\text{Ansewr A)}

m

m
m
x
\text{Figure 2}
d
\text{A projectile of mass $0.20 \mathrm{~kg}$ is fired with an initial speed of $20 \mathrm{~m} / \mathrm{s}$ at an angle of 60 degrees}
\text{ above the horizontal. The kinetic energy of the projectile at its highest point is:}
\hspace{-1mm}\text{A) $0 \mathrm{~J}$}\\
\text{B) $40 \mathrm{~J}$}\\
\text{C) $30 \mathrm{~J}$}\\
\hspace{1mm}\text{D) $5.0 \mathrm{~J}$}\\
\text{E) $10 \mathrm{~J}$}
\text{A projectile of mass $0.20 \mathrm{~kg}$ is fired with an initial speed of $20 \mathrm{~m} / \mathrm{s}$ at an angle of 60 degrees}
\text{ above the horizontal. The kinetic energy of the projectile at its highest point is:}
\text{Conservation of the mechanical energy:}
K_\text{i}+U_\text{i}=K_\text{f}+U_\text{f}
\displaystyle \frac{1}{2}mv_\text{i}^2+mgy_0=K_\text{f}+mgy
=
0
\text{The maximum height }\displaystyle H=\frac{v_i^2 \sin(\theta)^2}{2g}
(\text{Formula sheet})
\displaystyle \frac{1}{2}mv_\text{i}^2-mgH=K_\text{f}
\displaystyle \frac{1}{2}mv_\text{i}^2 (1-\sin^2\theta)=K_\text{f}
\displaystyle K_\text{f}=\frac{1}{2}mv_\text{i}^2 \cos^2\theta
\displaystyle K_\text{f}=\frac{1}{2} 0.20\times20^2\times \frac{1}{2^2}=10 \text{ J}
\text{Answer E)}
\Rightarrow
\Rightarrow
\Rightarrow
\Rightarrow
\text{A $2.2 \mathrm{~kg}$ block starts from rest on a rough inclined plane that makes an angle of $25^{\circ}$ with the}
\text{horizontal. The coefficient of kinetic friction is 0.25 . As the block slides $2.0 \mathrm{~m}$ down the plane, }
\text{the mechanical energy of the Earth-block system changes by:}
\text{A) $-11 \mathrm{~J}$}\\
\hspace{-2mm}\text{B) $+0 \mathrm{~J}$}\\
\hspace{0mm}\text{C) $+9.8 \mathrm{~J}$}\\
\text{D) $-18 \mathrm{~J}$}\\
\hspace{1mm}\text{E) $-9.8 \mathrm{~J}$}
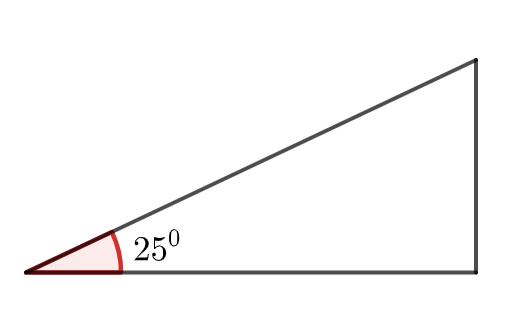
\text{A $2.2 \mathrm{~kg}$ block starts from rest on a rough inclined plane that makes an angle of $25^{\circ}$ with the}
\text{horizontal. The coefficient of kinetic friction is 0.25 . As the block slides $2.0 \mathrm{~m}$ down the plane, }
\text{the mechanical energy of the Earth-block system changes by:}
\Delta E_{\mathrm{mec}}+\Delta E_{\mathrm{th}}=0
\Delta E_{\mathrm{int}}=0
W(\vec{F}_N)=0
\text{The external force is }\vec{F}_N, \text{ so}
\Delta E_{\mathrm{th}}=f d=\mu_k N d=\mu_kmgd \cos\theta
\vec{F}_N
m\vec{g}
\vec{f}
\Delta E_{\mathrm{mec}}=-\Delta E_{\mathrm{th}}=-\mu_kmgd \cos\theta
=-0.25\times 2.2\times9.8\times2\times\cos(25^0)
=-0.25\times 2.2\times9.8\times2\times\cos(25^0)
=-9.8 \text{ J}
\text{Answer E)}
\text{A $6.0 \mathrm{~kg}$ box starts up a 30 degrees incline with $158 \mathrm{~J}$ of kinetic energy. How far will it slide up }
\text{the incline if the coefficient of kinetic friction between box and incline is 0.40 ?}
\text{A) $5.2 \mathrm{~m}$}\\
\text{B) $2.2 \mathrm{~m}$}\\
\text{C) $1.2 \mathrm{~m}$}\\
\text{D) $4.2 \mathrm{~m}$}\\
\text{E) $3.2 \mathrm{~m}$}
\text{A $6.0 \mathrm{~kg}$ box starts up a 30 degrees incline with $158 \mathrm{~J}$ of kinetic energy. How far will it slide up }
\text{the incline if the coefficient of kinetic friction between box and incline is 0.40 ?}
\Delta E_{\mathrm{mec}}+\Delta E_{\mathrm{th}}=0
\Delta K+\Delta U +\Delta E_{\mathrm{th}}=0
\Delta E_{\mathrm{th}}=f d=\mu_k N d=\mu_kmgd \cos\theta

\vec{F}_N
m\vec{g}
\vec{f}
\vec{v}
\Delta K=K_\text{f}-K_\text{i}=0-K_\text{i}=-158 \text{ J}
\Delta U =mg(y-y_0)=mgd \sin\theta
\Delta K+\Delta U +\Delta E_{\mathrm{th}}=0
\Rightarrow
\Delta K+mg h+\mu_kmgd \cos\theta=0
\displaystyle d=-\frac{\Delta K}{mg(\sin\theta+\mu_k \cos\theta)}=\frac{158}{6.0\times 9.8\times(\sin30^0+0.40\cos30^0)}\approx3.2 \text{ m}
\Rightarrow
\Delta K+mg d \sin\theta+\mu_kmgd \cos\theta=0
\text{Conservation of energy}
\text{Answer E)}
Chapter 8-Phys101
By smstry
Chapter 8-Phys101
- 404



