\text{Chapter 6}
\text{Chapter 6}
\text{Chapter 6}
\text{Chapter 6}
\begin{align*}
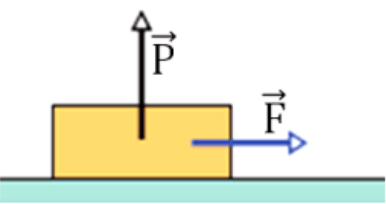
&\text{A }2.5\,\mathrm{kg}\text{ block is initially at rest on a horizontal surface. A horizontal force } \vec{F} \text{of magnitude}\\
&6.0\,\mathrm{N} \text{ and a vertical force } \vec{P} \text{ are then applied to the block as shown in Figure 5.}\\
&\text{The coefficients of friction for the block and surface are } \mu_s=0.40 \text{ and } \mu_k=0.25.\\
&\text{Determine the magnitude of the frictional force acting on the block if the magnitude of } \vec{P} \text{ is } 8.0\,\mathrm{N}.\\
&\\
&\text{A)}\ 6.0\,\mathrm{N}\qquad\\
&\text{B)}\ 6.6\,\mathrm{N}\qquad\\
&\text{C)}\ 4.1\,\mathrm{N}\qquad\\
&\text{D)}\ 8.0\,\mathrm{N}\qquad\\
&\text{E)}\ 9.8\,\mathrm{N}
\end{align*}
\begin{align*}
&\text{A }2.5\,\mathrm{kg}\text{ block is initially at rest on a horizontal surface. A horizontal force } \vec{F} \text{of magnitude}\\
&6.0\,\mathrm{N} \text{ and a vertical force } \vec{P} \text{ are then applied to the block as shown in Figure 5.}\\
&\text{The coefficients of friction for the block and surface are } \mu_s=0.40 \text{ and } \mu_k=0.25.\\
&\text{Determine the magnitude of the frictional force acting on the block if the magnitude of } \vec{P} \text{ is } 8.0\,\mathrm{N}.\\
&\\
\end{align*}

\text{The maximum friction force on the object before it moves is: }
f_\text{max}=\mu_s N= \mu_s(mg-P)=0.40\times (2.5\times 9.8-8)=6.6 \mathrm{~N}
\vec{f}
\text{The frictional force is therefore }
\text{since the pulling force $F\le f_\text{max}$, than the object is {\textbf{not moving}}}
f=F=6.0 \mathrm{~N}
\vec{N}
m\vec{g}
\begin{align*}
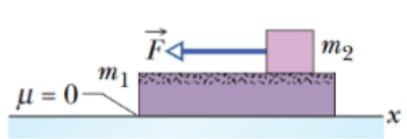
&\text{A slab of mass $m_1=40 \mathrm{~kg}$ rests on a frictionless floor, and a block of mass $m_2=10 \mathrm{~kg}$ }\\
&\text{rests on top of the slab. Between block and slab, the coefficient of static friction is 0.60 , }\\
&\text{and the coefficient of kinetic friction is 0.40 . A horizontal force $\vec{F}$ of magnitude 100 N }\\
&\text{begins to pull directly on the block, as shown. In unit-vector notation, what are the }\\
&\text{resulting accelerations of (a) the block and (b) the slab?}
\end{align*}
\overrightarrow{N}
m_2\vec{g}
m_1\vec{g}
\overrightarrow{f}
\overrightarrow{N'}
m_2\vec{g}
\overrightarrow{F}
\overrightarrow{f}
\text{free body diagram on }m_1
\text{free body diagram on }m_2
\overrightarrow{f}
\begin{align*}
&\text{A slab of mass $m_1=40 \mathrm{~kg}$ rests on a frictionless floor, and a block of mass $m_2=10 \mathrm{~kg}$ }\\
&\text{rests on top of the slab. Between block and slab, the coefficient of static friction is 0.60 , }\\
&\text{and the coefficient of kinetic friction is 0.40 . A horizontal force $\vec{F}$ of magnitude 100 N }\\
&\text{begins to pull directly on the block, as shown. In unit-vector notation, what are the }\\
&\text{resulting accelerations of (a) the block and (b) the slab?}
\end{align*}

\overrightarrow{N}
m_2\vec{g}
m_1\vec{g}
\overrightarrow{f}
\overrightarrow{N'}
m_2\vec{g}
\overrightarrow{F}
\overrightarrow{f}
\text{free body diagram on }m_1
\text{free body diagram on }m_2
\text{Mass }m_2:
m_2g=N'
f_\text{max}=\mu_sN'=\mu_s m_2 g=0.60\times 10\times 9.8=58.8N
F>f_\text{max}\Rightarrow m_2 \text{ will move}\Rightarrow\text{We use }\mu_k
\text{the projection on the x-axis gives}
\vec{F}+\vec{f}+\vec{N'}+m_2\vec{g}=m_2\vec{a}
x
F-f=m_2a\Rightarrow F-\mu_km_2g=m_2a\Rightarrow a=F/m_2-\mu_kg=100/10-0.4\times 9.8\approx6.1\text{ $m/s^2$}
\text{Mass }m_1:
\text{(Be careful: }f \text{ is not related to }\vec{N} \text{ because this } \vec{N} \text{ is from the surface below)}
\vec{f}+\vec{N}+m_2\vec{g}+m_1\vec{g}=m_1\vec{a}
\text{the projection on the x-axis gives}
{f}=m_1{a}\Rightarrow
\mu_k m_2 g=m_1{a}\Rightarrow a=\mu_k g m_2/m_1 =0.40\times 10/40 \times 9.8\approx1 \text{$m/s^2$}
\begin{align*}
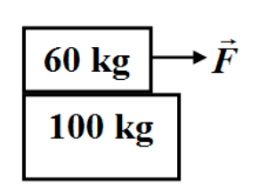
&\text{A }60\,\mathrm{kg}\text{ block slides along the top of a }100\,\mathrm{kg}\text{ block as shown in Figure~6. The 60 kg block }\\
&\text{has an acceleration of }3.0\,\mathrm{m\,s^{-2}}\text{ while a horizontal force }
\vec F=320\,\mathrm{N}\text{ is applied to it.}\\
&\text{There is no friction between the }100\,\mathrm{kg}\text{ block and the horizontal surface on which it stands,}\\
&\text{but there is friction between the two blocks. Find the magnitude of the acceleration}\\
&\text{of the }100\,\mathrm{kg}\text{ block during the time the two blocks remain in contact.}\\
&\\
&\text{A) }1.4\,\mathrm{m\,s^{-2}}\qquad\\
&\text{B) }2.0\,\mathrm{m\,s^{-2}}\qquad\\
&\text{C) }3.7\,\mathrm{m\,s^{-2}}\qquad\\
&\text{D) }1.6\,\mathrm{m\,s^{-2}}\qquad\\
&\text{E) }3.0\,\mathrm{m\,s^{-2}}
\end{align*}
\begin{align*}
&\text{A }60\,\mathrm{kg}\text{ block slides along the top of a }100\,\mathrm{kg}\text{ block as shown in Figure~6. The 60 kg block }\\
&\text{has an acceleration of }3.0\,\mathrm{m\,s^{-2}}\text{ while a horizontal force }
\vec F=320\,\mathrm{N}\text{ is applied to it.}\\
&\text{There is no friction between the }100\,\mathrm{kg}\text{ block and the horizontal surface on which it stands,}\\
&\text{but there is friction between the two blocks. Find the magnitude of the acceleration}\\
&\text{of the }100\,\mathrm{kg}\text{ block during the time the two blocks remain in contact.}\\
\end{align*}

\text{The frictions are playing opposit roles on the two objects.}
\text{They push the 100 kg object to move and slow down the}
\text{60 kg object.}
m\vec{g}
\vec{N}
\vec{f}
\text{60 kg block}
\vec{f}+\vec{N}+m\vec{g}+\vec{F}=m_1\vec{a}
\text{we project on x-axis}
-f+F=m_1 a
f=F-m_1 a=320-60\times 3=140 \mathrm{~N}
\begin{align*}
&\text{A }60\,\mathrm{kg}\text{ block slides along the top of a }100\,\mathrm{kg}\text{ block as shown in Figure~6. The 60 kg block }\\
&\text{has an acceleration of }3.0\,\mathrm{m\,s^{-2}}\text{ while a horizontal force }
\vec F=320\,\mathrm{N}\text{ is applied to it.}\\
&\text{There is no friction between the }100\,\mathrm{kg}\text{ block and the horizontal surface on which it stands,}\\
&\text{but there is friction between the two blocks. Find the magnitude of the acceleration}\\
&\text{of the }100\,\mathrm{kg}\text{ block during the time the two blocks remain in contact.}\\
\end{align*}

M\vec{g}
\vec{N}
\vec{f}
\text{100 kg block}
\vec{f}+\vec{N}+M\vec{g}+m_1\vec{g}=M\vec{a}_2
\text{we project on x-axis}
f=M a_2
a_2=\frac{f}{M}=\frac{140}{100}=1.4 \mathrm{~N}
\text{Notice how we took the opposit $\vec{f}$}
\begin{align*}
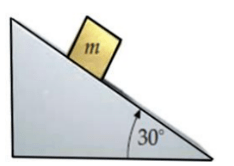
&\text{A block of mass } m \text{ is at rest on a plane inclined at }30^\circ \text{ with the horizontal, as shown in}\\
&\text{Fig. 5. Which of the following relations about the magnitude of the static friction force } f_s\\
&\text{ is necessarily TRUE?} \text{(Ignore air resistance.)}\\
&\\
&\text{A)}\ f_s = mg\sin 30^\circ\\
&\text{B)}\ f_s > mg\sin 30^\circ\\
&\text{C)}\ f_s > mg\\
&\text{D)}\ f_s > mg\cos 30^\circ\\
&\text{E)}\ f_s = mg\cos 30^\circ
\end{align*}
\begin{align*}
&\text{A block of mass } m \text{ is at rest on a plane inclined at }30^\circ \text{ with the horizontal, as shown in}\\
&\text{Fig. 5. Which of the following relations about the magnitude of the static friction force } f_s\\
&\text{ is necessarily TRUE?} \text{(Ignore air resistance.)}\\
\end{align*}

\text{at equilibrium we have }
\vec{N}+m\vec{g}+\vec{f}_s=0
\text{we project on y-axis:}
N-mg \cos\theta=0
\text{we project on x-axis:}
-f_s+mg \sin\theta=0
{f}_s^\text{max}=\mu_s N=\mu_s mg\cos\theta
f_s=mg \sin\theta
\text{Be careful, do not mix between $f_s$ and $f
_s^\text{max}$}
f_s^\text{max}>mg \sin\theta
\text{Answer A}
\vec{N}
m\vec{g}
\vec{f}
\text{A loaded penguin sled weighing $80 \mathrm{~N}$ rests on a plane inclined at an angle of $20^{\circ}$ to the horizontal.}
\text{Between the sled and the plane, the coefficient of static friction is 0.25 , and the coefficient of }
\text{kinetic friction is 0.15 .}
\text{a. What is the least magnitude of the force $F$, }
\text{ parallel to the plane, that will prevent the sled }
m\vec{g}+\vec{N}+\vec{f}+\vec{F}=m\vec{a}
\text{The force $\vec{F}$ prevents from slipping \textcolor{red}{down} so the friction $\vec{f}$ should be \textcolor{red}{upward}}
\text{We project on x-axis (along the incline)}
-mg \sin(20^0)+f_\text{max}+F=0
f_\text{max}=\mu_sN=\mu_s mg \cos(20^0)
F=mg(\sin(20^0)-\mu_s\cos(20))=80( 0.34-0.25\times0.94)=8.6 N
\text{from slipping down the plane?}
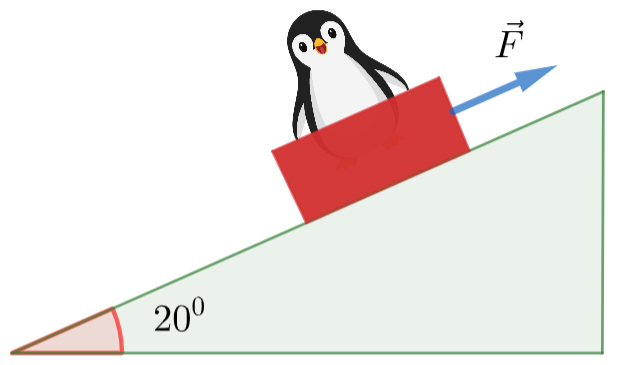
\text{A loaded penguin sled weighing $80 \mathrm{~N}$ rests on a plane inclined at an angle of $20^{\circ}$ to the horizontal.}
\text{Between the sled and the plane, the coefficient of static friction is 0.25 , and the coefficient of }
\text{kinetic friction is 0.15 .}
m\vec{g}+\vec{N}+\vec{f}+\vec{F}=m\vec{a}
\text{The force F wants to start the mass moving up so the friction $\vec{f}$ should be \textcolor{red}{downward}}
\text{We project on x-axis (along the incline)}
-mg \sin(20^0)-f_\text{max}+F=0
f_\text{max}=\mu_sN=\mu_s mg \cos(20^0)
F=mg(\sin(20^0)+\mu_s\cos(20))=80( 0.34 0.25\times0.94)=46.2 N
\text{b) What is the minimum magnitude of $F$ that will start }
\text{the sled moving up the plane?}

\text{A loaded penguin sled weighing $80 \mathrm{~N}$ rests on a plane inclined at an angle of $20^{\circ}$ to the horizontal.}
\text{Between the sled and the plane, the coefficient of static friction is 0.25 , and the coefficient of }
\text{kinetic friction is 0.15 .}
m\vec{g}+\vec{N}+\vec{f}+\vec{F}=m\vec{a}
\text{The force F moves the mass up at a constant $v$, the friction $\vec{f}$ should be \textcolor{red}{downward}}
\text{We project on x-axis (along the incline)}
-mg \sin(20^0)-f+F=0
f=\mu_k N=\mu_k mg \cos(20^0)
F=mg(\sin(20^0)+\mu_k\cos(20))=80( 0.34 +0.15\times0.94)=38.6N
\text{c) What value of $F$ is required to move the sled up ?}
\text{the plane at constant velocity?}


\text{At what angle should cad cular roadway of 50 m radius, be banked to allow cars to round}\\
\text{the curve without slip rig at $12 \mathrm{~m} / \mathrm{s}$ ? (Ignore friction)}
\begin{align*}
A)& 16^{\circ}\\
B)& 10^{\circ}\\
C)& 33^{\circ}\\
D)& 27^{\circ}\\
E)& 90^{\circ}
\end{align*}

m\vec{g}
\vec{N}
\vec{a}
\vec{N}+m\vec{g}=m\vec{a}
\text{The car is not sliding. It is rotating on a banked road (like in formula 1)}\\
\text{That is why $\vec{a}$ is horizontal towards the center of rotation.}
x
\text{Projecting on x-axis}
mg \cos\theta=m a \sin \theta
\Rightarrow g\sin\theta =\frac{v^2}{R}\cos\theta
\Rightarrow \tan\theta=\frac{v^2}{Rg}=\frac{12^2}{50\times 9.8}=0.2938
\Rightarrow \theta=\tan^{-1}(0.2938)=16.37^0

\text{At what angle should have a circular roadway of 50 m radius, be banked to allow cars to round}\\
\text{the curve without slip rig at $12 \mathrm{~m} / \mathrm{s}$ ? (Ignore friction)}
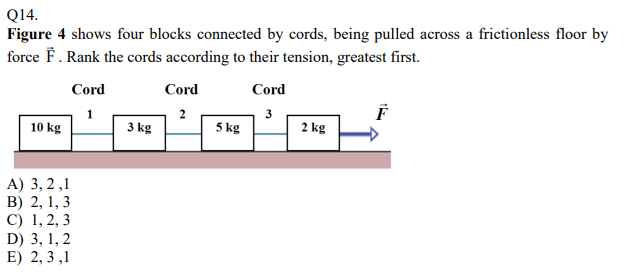
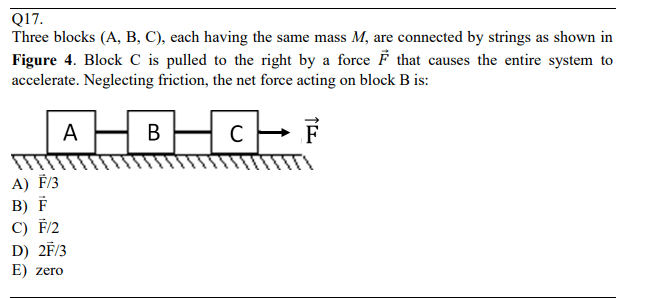
Chapter 6-Phys101
By smstry
Chapter 6-Phys101
- 381



