Major II
\text{Major II}
Sommerfeld-Watson transformation
\text{Sommerfeld-Watson transformation}
Branch-cuts and integration
\text{Branch-cuts and integration}
Linear ODEs
\text{Linear ODEs}
Beta and Gamma functions
\text{Beta and Gamma functions}
Evaluate the following integral using complex integration techniques.
\text{ Evaluate the following integral using complex integration techniques.}\\
I(p)=∫0+∞1+(x+1)2xpdx,
\displaystyle I(p)=\int_0^{+\infty} \frac{x^p}{1+(x+1)^2} d x,
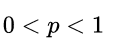
Problem 1:
\text{Problem 1:}
∮f(z)dz=2πi∑Res(f(z))
\displaystyle \oint f(z) d z=2 \pi i \sum \operatorname{Res}(f(z))
(z+1)2−i2=0
(z+1)^2-i^2=0
z1=−1+i,z2=−1−i
z_1=-1+i, z_2=-1-i
Res(f(z),z1)=z1−z2z1p=2ie3i4πp22p
\displaystyle \operatorname{Res}\left(f(z), z_1\right)=\frac{z_1^p}{z_1-z_2}=\frac{e^{3 i \frac{\pi}{4} p}}{2 i} 2^{\frac{p}{2}}
Res(f(z),z2)=z2−z1z2p=−2ie45πip22p
\displaystyle \operatorname{Res}\left(f(z), z_2\right)=\frac{z_2^p}{z_2-z_1}=\frac{e^{\frac{5\pi i}{4} p}}{-2 i} 2^{\frac{p}{2}}
∮f(z)dz=π(e3i4πp−e5i4πp)2p/2
\displaystyle \oint f(z) d z=\pi\left(e^{3 i \frac{\pi}{4} p}-e^{5 i \frac{\pi}{4} p}\right) {2}^{p/2}
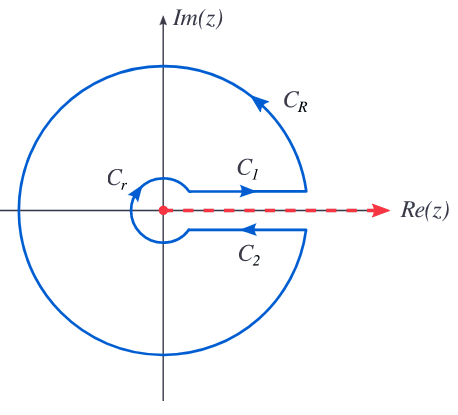
∮f(z)dz=∫C1f(z)dz+∫C2f(z)dz+∫Crf(z)dz+∫CRf(z)dz
\displaystyle \oint f(z) d z=\int_{C_1} f(z) d z+\int_{C_2} f(z) d z+\int_{C_r} f(z) d z+\int_{C_R} f(z) d z
Optional (+0.25 pts): Find the limit when p→0
\text{Optional (+0.25 pts): Find the limit when }p\rightarrow 0
(1−e2iπp)I=π(e34iπp−e45iπp)2p/2
\displaystyle \left(1-e^{2 i \pi p}\right) I=\pi\left(e^{3 \frac{ i \pi p}{4}}-e^{\frac{5 i\pi p}{4}}\right) 2^{p / 2}
I=eiπpπ−2isin(πp)eiπp(e−2i8πp−e+2i8πp)22p
\displaystyle I=\frac{\pi}{e^{i \pi p}} \frac{e^{i \pi p}\left(e^{-2 i \frac{\pi p}{8}}-e^{+2 i \frac{\pi p}{8}}\right)}{-2 i \sin (\pi p)} 2^{\frac{p}{2}}
I=2p/2πsin(πp)sin(4πp)
\displaystyle I=2^{p / 2} \pi \quad \frac{\sin \left(\frac{\pi p}{4}\right)}{\sin (\pi p)}
∫c2f(z)dz=∫∞0(x+1)2+1xei2πpdx=−ei2πpI
\displaystyle \int_{c_2} f(z) d z=\int_{\infty}^0 \frac{x e^{i 2 \pi p}}{(x+1)^2+1} d x=-e^{i 2 \pi p} I
∫c1f(z)dx=∫f(x)dx=I
\displaystyle \int_{c_1} f(z) d x=\int f(x) d x=I
2) The limit
\text{2) The limit}
since sinx≈x
\text{since }\sin x\approx x
I≈π(πp)(4πp)→π/4
\displaystyle I \approx \pi \quad \frac{ \left(\frac{\pi p}{4}\right)}{ (\pi p)}\rightarrow \pi/4
(The integrals on Cr and CR vanish at he two,limits )
(\text{The integrals on }C_r \text{ and }C_R \text{ vanish at he two,limits })
Problem 2:
\text{Problem 2:}
Let us consider the following integral:
\text{Let us consider the following integral:}
I(p,q)=∫0∞∣1−x∣qxpdx
\displaystyle I(p,q)=\int_0^\infty \frac{x^p}{|1-x|^q}dx
1) Separate the integral to two intervals [0,1] and [1,+∞[
\text{1) Separate the integral to two intervals }[0,1]\text{ and }[1,+\infty[
2) Make the change of variable x=u1 for the second integral.
\displaystyle \text{2) Make the change of variable }x=\frac{1}{u} \text{ for the second integral.}
3) Express now I(p,q) using Beta functions
\text{3) Express now } I(p,q) \text{ using Beta functions}
4) Calculate the result for p=1/4,q=1/2,as function of Γ(1/4) alone
\displaystyle \text{4) Calculate the result for }p=1/4, q=1/2,\text{as function of }\Gamma{(1/4)}\text{ alone }
5) Calculate the limit for p,q→∞ with the constraint p−q=21 with p,q non integrers
\text{5) Calculate the limit for } p,q \rightarrow \infty \text{ with the constraint }p-q=\frac{1}{2} \text{ with } p, q \text{ non integrers}
Solution:
\text{Solution:}
∫0∞∣1−x∣qxpdq=∫01∣1−x∣qxpdx+∫1+∞∣1−x∣qxpdx.
\displaystyle \int_0^{\infty} \frac{x^p}{|1-x|^q} d q=\int_0^1 \frac{x^p}{|1-x|^q} d x+\int_1^{+\infty} \frac{x^p}{|1-x|^q} d x .
u=x1⇒dx=−u2du
\displaystyle u=\frac{1}{x} \Rightarrow d x=-\frac{d u}{u^2}
∫1∞∣1−x∣qxpdx=∫01∣1−u1∣qu−pu2du=∫01∣1−u∣quq−p−2du
\displaystyle \int_1^{\infty} \frac{x^p}{|1-x|^q} d x=\int_0^1 \frac{u^{-p}}{|1-\frac{1}{u}|^q} \frac{d u}{u^2}=\int_0^1 \frac{u^{q-p-2}}{|1-u|^q} d u
=B(q−p−1,1−q)
\displaystyle =B(q-p-1,1-q)
I(p,q)=B(q−p−1,1−q)+B(p+1,1−q)
\displaystyle I(p, q)= B(q-p-1,1-q)+B(p+1,1-q)
I(1/4,1/2)=B(−3/4,1/2)+B(5/4,1/2)
\displaystyle I(1/4,1/2)= B(-3/4,1/2)+B(5/4,1/2)
I(1/4,1/2)=Γ(−1/4)Γ(−3/4)Γ(1/2)+Γ(7/4)Γ(5/4)Γ(1/2)
\displaystyle I(1/4,1/2)= \frac{\Gamma(-3/4)\Gamma(1/2)}{\Gamma(-1/4)}+\frac{\Gamma(5/4)\Gamma(1/2)}{\Gamma(7/4)}
I(1/4,1/2)=32πΓ(1/4)2+32πΓ(1/4)2
\displaystyle I(1/4,1/2)= \frac{\Gamma(1/4)^2}{3\sqrt{2\pi}} +\frac{\Gamma(1/4)^2}{3\sqrt{2\pi}}
Γ(3/4)Γ(1/4)=π/sin(π/4)=π2
\Gamma(3/4)\Gamma(1/4)=\pi/\sin(\pi/4)=\pi\sqrt{2}
Γ(5/4)=(1/4)Γ(1/4)
\Gamma(5/4)=(1/4) \Gamma(1/4)
Γ(1/4)=(−3/4)Γ(−3/4)
\Gamma(1/4)=(-3/4) \Gamma(-3/4)
Γ(3/4)=(−1/4)Γ(−1/4)
\Gamma(3/4)=(-1/4) \Gamma(-1/4)
Γ(z+1)=zΓ(z);
\Gamma(z+1)=z \Gamma(z) ;
Γ(z)Γ(1−z)=sinπzπ
\displaystyle \Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin{\pi z}}
Γ(7/4)=(3/4)Γ(3/4)=(4Γ(1/4))3π2
\Gamma(7/4)=(3/4) \Gamma(3/4) =\frac{3\pi\sqrt{2}}{(4\Gamma(1/4))}
I(1/4,1/2)=232πΓ(1/4)2
\displaystyle I(1/4,1/2)= 2 \frac{\Gamma(1/4)^2}{3\sqrt{2\pi}}
Evaluate the following sum:
\text{Evaluate the following sum:}
S(a)=n=−∞∑∞(n−a)2+11
\displaystyle S(a)=\sum_{n=-\infty}^{\infty} \frac{1}{(n-a)^2+1}
Problem 3:
\text{Problem 3:}
Optional: What is the limit when a→0
\text{Optional: What is the limit when }a\rightarrow 0
Solution:
\text{Solution:}
F(z)=(z−a)2+1πsinπzcosπz
\displaystyle F(z)=\frac{\pi}{(z-a)^2+1} \frac{\cos \pi z}{\sin \pi z}
The poles of f(z) are: z1=a+i,z2=a−i
\text{The poles of }f(z) \text{ are: } z_1=a+i, z_2=a-i
zi∑Res(F(z),zi)=(z1−z2)πsinπz1cosπz1+(z2−z1)πsinπz2cosπz2
\displaystyle \sum_{z_i} \text{Res}(F(z),z_i)=\frac{\pi}{\left(z_1-z_2\right)} \frac{\cos \pi z_1}{\sin \pi z_1}+\frac{\pi}{\left(z_2-z_1\right)} \frac{\cos \pi z_2}{\sin \pi z_2}
=(z1−z2)π(sinπz1cosπz1−sinπz2cosπz2)
\displaystyle =\frac{\pi}{\left(z_1-z_2\right)}\Bigg( \frac{\cos \pi z_1}{\sin \pi z_1}- \frac{\cos \pi z_2}{\sin \pi z_2}\Big)
=−πi2sinπz1sinπz2cosπz1sinπz2−cosπz2sinπz1
\displaystyle =-\pi i \frac{\cos \pi z_1 \sin \pi z_2- \cos \pi z_2 \sin \pi z_1}{2\sin \pi z_1 \sin \pi z_2}
=−πi2sinπz1sinπz2sinπ(z2−z1)
\displaystyle =-\pi i \frac{\sin \pi (z_2-z_1)}{2\sin \pi z_1 \sin \pi z_2}
=πi2sinπz1sinπz2sin2πi
\displaystyle =\pi i \frac{\sin 2\pi i }{2\sin \pi z_1 \sin \pi z_2}
n=−∞∑n=+∞f(n)=−πicosh2π−cos2πaisinh2π→πcosh2π−1sinh2π=πcoth(π)
\displaystyle \sum_{n=-\infty}^{n=+\infty} f(n)= -\pi i \frac{i\sinh 2\pi }{\cosh 2\pi - \cos 2\pi a}\rightarrow \pi \frac{\sinh 2\pi }{\cosh 2\pi - 1}=\pi \coth(\pi)
=πi(cosπ(z1−z2)−cosπ(z1+z2))sin2πi
\displaystyle =\pi i \frac{\sin 2\pi i }{(\cos \pi (z_1-z_2)- \cos \pi (z_1+z_2))}
=πi(cos2πi−cos2πa)sin2πi
\displaystyle =\pi i \frac{\sin 2\pi i }{(\cos 2\pi i - \cos 2\pi a)}
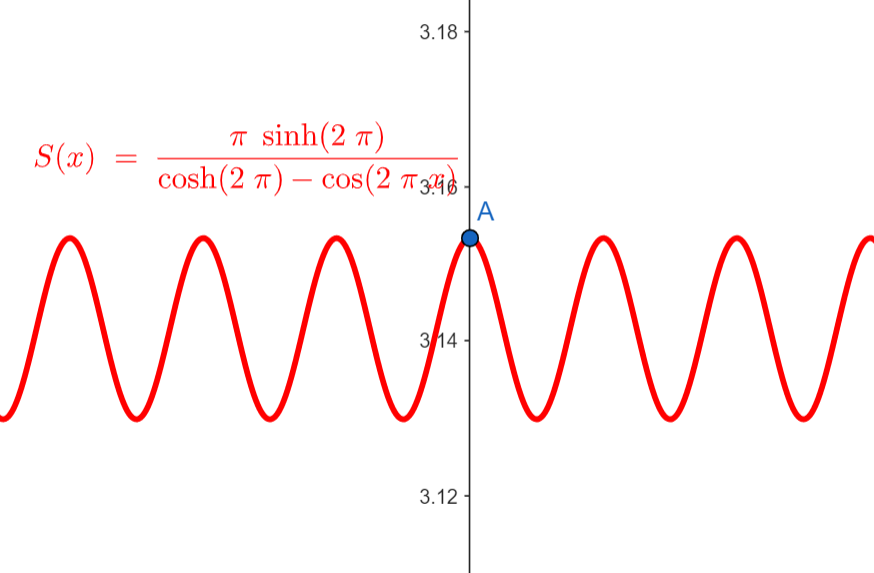
As we can see in this figure, the sum oscillates as function of a.
\text{As we can see in this figure, the sum oscillates as function of a.}
Problem 4:
\text{Problem 4:}
Solve the following isobaric ODE
\text{Solve the following isobaric ODE}
dxdy=2yx−(y2+x2)
\displaystyle \frac{d y}{d x}=\frac{-\left(y^2+\frac{2}{x}\right)}{2 y x}
Solution:
\text{Solution:}
2yxdy=−(y2+x2)dx
\displaystyle 2 y x d y=-\left(y^2+\frac{2}{x}\right) dx
we find that 2m+1=0⇒m=−1/2
\text{we find that } 2m+1=0\Rightarrow m=-1/2
y=vx−1/2⇒y2=v2/x⇒2ydy=2vdv/x−v2dx/x2
y=vx^{-1/2}\Rightarrow y^2=v^2 /x \Rightarrow 2 y dy=2vdv/x-v^2 dx/x^2
2vdv−v2dx/x=−(v2/x+2/x)dx⇒vdv=−dx/x
2vdv-v^2 dx/x =-(v^2/x+2/x) dx\Rightarrow v dv=-dx/x
The equation (1) becomes:
\text{The equation (1) becomes:}
(1)
(1)
⇒v2=−2lnx−2c
\Rightarrow v^2=-2\ln x -2c
⇒y2x=−2lncx
\Rightarrow y^2 x=-2\ln cx
⇒y=(−2xln(c/x))1/2
\displaystyle \Rightarrow y =\Big(-2\frac{\ln (c/x)}{x}\Big)^{1/2}
Problem 5:
\text{Problem 5:}
Let us solve the following non-linear ODE:
\text{Let us solve the following \textbf{non-linear} ODE:}
y′+xy=yx2+x
\displaystyle y'+x y=\frac{x^2+x}{y}
1) Make the change of variable u=1+y2
\text{1) Make the change of variable }u=1+y^2
2) Solve the ODE with the variable u
\text{2) Solve the ODE with the variable }u
3)Find y.
3) \text{Find }y.
Solution
\text{Solution}
y′+xy=yx2+x
\displaystyle y'+x y=\frac{x^2+x}{y}
u=1+y2⇒u′=2yy′
u=1+y^2\Rightarrow u'=2y y'
u′+2x(u−1)=2(x2+x)
u'+2x(u-1)=2(x^2+x)
⇒u′+2xu=2x2+4x
\Rightarrow u'+2 x u =2x^2+4x
u(x)=λe−x2
u(x)=\lambda e^{-x^2}
the homogeneous solution is
\text{the homogeneous solution is }
variation of the constant
\text{variation of the constant}
λ′e−x2−2xλe−x2+2xλe−x2=2x2+4x
\lambda' e^{-x^2}-2x \lambda e^{-x^2}+2x \lambda e^{-x^2}=2x^2+4x
λ′=ex2(2x2+4x)
\lambda'= e^{x^2}(2x^2+4x)
λ=∫xes2(2s2+4s)ds=F(x)
\displaystyle \lambda= \int^x e^{s^2}(2s^2+4s) ds =F(x)
u(x)=F(x)e−x2
u(x) =F(x)e^{-x^2}
y(x)=(F(x)e−x2−1)21
y(x) =(F(x)e^{-x^2}-1)^\frac{1}{2}
Let us solve the following differential equation:
\text{Let us solve the following differential equation: }
y′′+y′−2y=ex+x
y^{\prime \prime}+y^{\prime}-2 y=e^x+x
Problem 6:
\text{Problem 6:}
1) Find the solution for the homogeneous equation.
\text{1) Find the solution for the homogeneous equation.}
2) Find the Wronskian.
\text{2) Find the Wronskian. }
3) Find the particular solution.
\text{3) Find the particular solution. }
4) Express the general solution.
\text{4) Express the general solution.}
The characteristic polynomial is:
\text{The characteristic polynomial is:}
m2+m−2=0
m^2+m-2=0
Solution:
\text{Solution:}
the roots are: m1=1,m2=−2
\text{the roots are: } m_1=1,m_2=-2
the solutions for the homogeneous equation are:
\text{the solutions for the homogeneous equation are:}
ex and e−2x
e^x \text{ and } e^{-2x}
W(x)=exexe−2x−2e−2x=−2e−x−e−x=−3e−x
\displaystyle
W(x)=
\begin{vmatrix}
e^x & e^{-2x} \\
e^x & -2e^{-2x}
\end{vmatrix}
=-2e^{-x}-e^{-x}=-3e^{-x}
yp(x)=−31(e−2x∫xe2sF(s)ds−ex∫xe−sF(s)ds)
\displaystyle y_p(x)=-\frac{1}{3}\Big(e^{-2x}\int^x e^{2s} F(s) ds-e^x\int^x e^{-s} F(s) ds \Big)
yp(x)=−31(e−2x∫x(e3s+se2s)ds−ex∫x(1−se−s)ds)
\displaystyle y_p(x)=-\frac{1}{3}\Big(e^{-2x}\int^x (e^{3s}+s e^{2s}) ds-e^x\int^x (1-se^{-s}) ds \Big)
yp(x)=−31(((ex/3+(e−2x+(2x−1))/4))−(xex−(ex+(x+1))))
\displaystyle y_p(x)=-\frac{1}{3}\Big( \Big((e^{x}/3+(e^{-2x}+(2x-1))/4) \Big) -(xe^x -(e^x +(x+1))) \Big)
y(x)=Aex+Be−2x+yp(x)
y(x)=A e^x+Be^{-2x}+y_p(x)
1+i=2eiπ/4
1+i=\sqrt{2}e^{i\pi/4}
−1+i=2ei3π/4
-1+i=\sqrt{2}e^{i3\pi/4}
−1−i=2ei5π/4
-1-i=\sqrt{2}e^{i5\pi/4}
1−i=2ei7π/4
1-i=\sqrt{2}e^{i7\pi/4}
eiθ1+eiθ2=2ei2θ1+θ2cos(2θ1−θ2)
\displaystyle e^{i\theta_1}+e^{i\theta_2}=2e^{i\frac{\theta_1+\theta_2}{2}} \cos{\Bigg(\frac{\theta_1-\theta_2}{2}\Bigg)}
eiθ1−eiθ2=2iei2θ1+θ2sin(2θ1−θ2)
\displaystyle e^{i\theta_1}-e^{i\theta_2}=2ie^{i\frac{\theta_1+\theta_2}{2}} \sin{\Bigg(\frac{\theta_1-\theta_2}{2}\Bigg)}
cosθ=2eiθ+e−iθ
\displaystyle \cos{\theta}=\frac{e^{i\theta}+e^{-i\theta}}{2}
sinθ=2ieiθ+e−iθ
\displaystyle \sin{\theta}=\frac{e^{i\theta}+e^{-i\theta}}{2i}
i=eiπ/2
i=e^{i\pi/2}
−1=eiπ
-1=e^{i\pi}
z=∣z∣eiarg(z)
z=|z|e^{i\text{arg}(z)}
2ℜ(z)=z+z
2\Re(z)=z+\overline z
2iℑ(z)=z−z
2i\Im(z)=z-\overline z
Γ(z)Γ(1−z)=sinπzπ
\displaystyle \Gamma(z) \Gamma(1-z)=\frac{\pi}{\sin \pi z}
Γ(21)=π
\displaystyle \Gamma\Big(\frac{1}{2}\Big)=\sqrt{\pi}
Γ(z)Γ(z+21)=21−2zπΓ(2z)
\Gamma(z) \Gamma\left(z+\frac{1}{2}\right)=2^{1-2 z} \sqrt{\pi} \Gamma(2 z)
Γ(z)≡∫0∞e−ttz−1dt,Re(z)>0
\displaystyle \Gamma(z) \equiv \int^{\infty}_{0} e^{-t} t^{z-1} d t,\hspace{0.15 cm} \text{Re}(z)>0
Γ(z+1)∼2πz(ez)z,z→∞
\displaystyle \Gamma(z+1) \sim \sqrt{2 \pi z}\left(\frac{z}{e}\right)^z, z\rightarrow \infty
B(a,b)=Γ(a+b)Γ(a)Γ(b)
\displaystyle \mathcal{B}(a, b)=\frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}
yp(x)=y2(x)∫xW{y1(s),y2(s)}y1(s)F(s)ds−y1(x)∫xW{y1(s),y2(s)}y2(s)F(s)ds
\displaystyle y_p(x)=y_2(x) \int^x \frac{y_1(s) F(s) d s}{W\left\{y_1(s), y_2(s)\right\}}-y_1(x) \int^x \frac{y_2(s) F(s) d s}{W\left\{y_1(s), y_2(s)\right\}}
B(x,y)=∫01tx−1(1−t)y−1dt
\displaystyle \mathcal{B}(x, y)=\int_0^1 t^{x-1}(1-t)^{y-1} d t
B(x,y)=2∫0π/2(sinθ)2x−1(cosθ)2y−1dθ
\displaystyle \mathcal{B}(x, y)=2 \int_0^{\pi / 2}(\sin \theta)^{2 x-1}(\cos \theta)^{2 y-1} d \theta
for x,y>0
\text { for } x, y>0
∫xeaxdx=a21+eax(ax−1)
\displaystyle \int x e^{a x} dx=\frac{1+e^{a x}(a x-1)}{a^2}
F(z)=πf(z)sin(πz)cos(πz)
\displaystyle F(z)=\pi f(z) \frac{\cos (\pi z)}{\sin (\pi z)}
n=−∞∑n=+∞f(n)=−i∑Res(F(z),z=zi)
\displaystyle \sum_{n=-\infty}^{n=+\infty} f(n)=-\sum_i \operatorname{Res}\left(F(z), z=z_i\right)
cos(ix)=cosh(x)
\displaystyle \cos(i x)=\cosh(x)
sin(ix)=isinh(x)
\displaystyle \sin(i x)=i \sinh(x)
sin(x)≈x
\sin(x)\approx x
cos(x)≈1−x2/2
\cos(x)\approx 1-x^2/2
M a j o r I I \text{Major II} S o m m e r f e l d - W a t s o n t r a n s f o r m a t i o n \text{Sommerfeld-Watson transformation} B r a n c h - c u t s a n d i n t e g r a t i o n \text{Branch-cuts and integration} L i n e a r O D E s \text{Linear ODEs} B e t a a n d G a m m a f u n c t i o n s \text{Beta and Gamma functions}
deck
By smstry
deck
- 130