\text{Chapter 20}
\text{Chapter 20}
\text{Chapter 20}
\text{Chapter 20}
\text{Find the change in entropy of a $100 \mathrm{~g}$ of ice at $0^{\circ} \mathrm{C}$ that is isobarically heated slowly to }
\text{reach $80^{\circ} \mathrm{C}$ water.}
\text{[The heat of fusion for ice $L_F=80\hspace{1mm} \mathrm{cal} / \mathrm{g}$ and the specific heat of water $\left.c_w=1.0 \hspace{1mm} \mathrm{cal} / \mathrm{g} . \mathrm{K}\right]$.}
\text{A) $55\hspace{1mm} \mathrm{cal} / \mathrm{K}$}
\text{B) $12\hspace{1mm} \mathrm{cal} / \mathrm{K}$}
\text{C) $62\hspace{1mm} \mathrm{cal} / \mathrm{K}$}
\text{D) $35 \hspace{1mm}\mathrm{cal} / \mathrm{K}$}
\text{E) $85 \hspace{1mm}\mathrm{cal} / \mathrm{K}$}
\text{Find the change in entropy of a $100 \mathrm{~g}$ of ice at $0^{\circ} \mathrm{C}$ that is isobarically heated slowly to }
\text{reach $80^{\circ} \mathrm{C}$ water.}
\text{[The heat of fusion for ice $L_F=80\hspace{1mm} \mathrm{cal} / \mathrm{g}$ and the specific heat of water $c_w=1.0 \hspace{1mm} \mathrm{cal} / \mathrm{g} . \mathrm{K}$]}
\text{A) $55\hspace{1mm} \mathrm{cal} / \mathrm{K}$}
\begin{aligned}
& \Delta \mathrm{S}=\frac{\mathrm{mL_F}}{\mathrm{T}}+\mathrm{mc_w} \ln \frac{\mathrm{T}_{\mathrm{f}}}{\mathrm{T}_{\mathrm{i}}} \\
& =\frac{100 \times 80}{273}+100 \times 1 \ln \frac{273+80}{273}=55 \hspace{1mm}\mathrm{cal} / \mathrm{K}
\end{aligned}
\text{We keep $m$ in grams because of the units of $c_w$}
\text{ice at $0^0$}
\text{water at $80^0$}
\rightarrow
\rightarrow
Q_1=mL_F
Q_2=mc\Delta T
\text{heating}
\text{melting}
\text{ice at $0^0$}
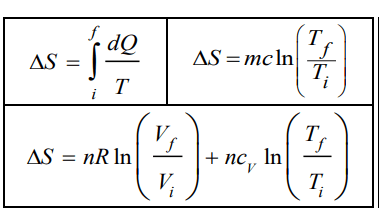
\text{formula sheet}
\text{Five moles of an ideal monatomic gas are allowed to expand isobarically. The initial volume}
\text{is $20.0 \mathrm{~cm}^3$ and the final volume is $100 \mathrm{~cm}^3$. Find the change in entropy of the gas.}
\text{A) $167 \mathrm{~J} / \mathrm{K}$}
\text{B) $100 \mathrm{~J} / \mathrm{K}$}
\text{C) $66.9 \mathrm{~J} / \mathrm{K}$}
\text{D) $234 \mathrm{~J} / \mathrm{K}$}
\text{E) $33.4 \mathrm{~J} / \mathrm{K}$}
\begin{aligned}
& \Delta S=n R \ln \frac{V_f}{V_i}+\mathrm{nC}_{\mathrm{v}} \ln \frac{\mathrm{T}_{\mathrm{f}}}{\mathrm{T}_{\mathrm{i}}} \\
& \mathrm{pV}=\mathrm{nRT} \Rightarrow \frac{\mathrm{V}_{\mathrm{f}}}{\mathrm{V}_{\mathrm{i}}}=\frac{\mathrm{T}_{\mathrm{f}}}{\mathrm{T}_{\mathrm{i}}} \\
& \Delta \mathrm{S}=\mathrm{nR} \ln \frac{\mathrm{V}_{\mathrm{f}}}{\mathrm{V}_{\mathrm{i}}}+\mathrm{nC}_{\mathrm{v}} \ln \frac{\mathrm{V}_{\mathrm{f}}}{\mathrm{V}_{\mathrm{i}}} \\
&=\mathrm{n}\left(R+\mathrm{C}_{\mathrm{v}}\right) \ln \frac{\mathrm{V}_{\mathrm{f}}}{\mathrm{V}_{\mathrm{i}}}=5\left(\frac{5}{2}\right)(8.31) \ln \frac{100}{20}=167 \mathrm{~J} / \mathrm{K}
\end{aligned}
\text{Five moles of an ideal monatomic gas are allowed to expand isobarically. The initial volume}
\text{is $20.0 \mathrm{~cm}^3$ and the final volume is $100 \mathrm{~cm}^3$. Find the change in entropy of the gas.}
\text{A) $167 \mathrm{~J} / \mathrm{K}$}
\text{B) $100 \mathrm{~J} / \mathrm{K}$}
\text{C) $66.9 \mathrm{~J} / \mathrm{K}$}
\text{D) $234 \mathrm{~J} / \mathrm{K}$}
\text{E) $33.4 \mathrm{~J} / \mathrm{K}$}
\text{The change in entropy of 20.0 moles of an ideal monatomic gas in a constant volume process is $200 \mathrm{~J} / \mathrm{K}$.}
\text{If the initial temperature of the gas was $300 \mathrm{~K}$, what is its final temperature?}
\text{A) $669 \mathrm{~K}$}
\text{B) $562 \mathrm{~K}$}
\text{C) $427 \mathrm{~K}$}
\text{D) $187 \mathrm{~K}$}
\text{E) $345 \mathrm{~K}$}
\text{The change in entropy of 20.0 moles of an ideal monatomic gas in a constant volume process is $200 \mathrm{~J} / \mathrm{K}$.}
\text{If the initial temperature of the gas was $300 \mathrm{~K}$, what is its final temperature?}
\text{At constant volume $V_f=V_i$}
\Delta S=n C_{\mathrm{v}} \ln \left(\frac{T_f}{T_i}\right) \Rightarrow \frac{T_f}{T_i}=e^{\frac{\Delta S}{n C_v}}
\displaystyle \mathrm{~T}_{\mathrm{f}}=\mathrm{T}_{\mathrm{i}} e^{\displaystyle\frac{\Delta \mathrm{S}}{n\mathrm{c}_{\mathrm{v}}}}=300 \times \mathrm{e}^{\displaystyle\frac{200}{20 \times \frac{5}{2} \times 8.314}}=668.9 \mathrm{~K}
\text{A refrigerator rejects $35.0 \mathrm{~kJ}$ of heat to the room during each cycle and operates with }
\text{coefficient of performance of 4.60 . What is the work done per cycle?}
\text{A) $6.25 \mathrm{~kJ}$}
\text{B) $7.61 \mathrm{~kJ}$}
\text{C) $0.131 \mathrm{~kJ}$}
\text{D) $10.2 \mathrm{~kJ}$}
\text{E) $161 \mathrm{~kJ}$}
\begin{aligned}
& K=\frac{|Q_L|}{|W|}=\frac{|Q_H|-|W|}{|W|} \Rightarrow K |W|=|Q_H|-|W| \\
& |W|(K+1)=|Q_H| \Rightarrow |W|=\frac{|Q_H|}{k+1}=\frac{35000}{5.6} \\
& |W|=6250 J
\end{aligned}
\text{A refrigerator rejects $35.0 \mathrm{~kJ}$ of heat to the room during each cycle and operates with }
\text{coefficient of performance of 4.60 . What is the work done per cycle?}
\text{A) $6.25 \mathrm{~kJ}$}
\text{B) $7.61 \mathrm{~kJ}$}
\text{C) $0.131 \mathrm{~kJ}$}
\text{D) $10.2 \mathrm{~kJ}$}
\text{E) $161 \mathrm{~kJ}$}
\text{The operating temperature of a Carnot refrigerator is $2.0^{\circ} \mathrm{C}$. The refrigerator is placed in}
\text{a kitchen where the temperature is $22^{\circ} \mathrm{C}$. What power is needed to operate this refrigerator}
\text{in order to extract from it $89 \mathrm{MJ}$ of heat in one hour?}
\text{A) $1.8 \mathrm{~kW}$}
\text{B) $2.0 \mathrm{~kW}$}
\text{C) $1.5 \mathrm{~kW}$}
\text{D) $2.9 \mathrm{~kW}$}
\text{E) $1.0 \mathrm{~kW}$}
K=\frac{Q_L}{W}
Q_L=89 MJ
W=\frac{Q_L}{K}=\frac{89 \times 10^6}{13.75}=6.47\times 10^6 W
K=\frac{T_L}{T_H-T_L}=\frac{2+273}{20}=13.75
P=\frac{W}{t}=\frac{6.47}{3600}\times 10^6=1.8 \text{ kW}
\text{The operating temperature of a Carnot refrigerator is $2.0^{\circ} \mathrm{C}$. The refrigerator is placed in}
\text{a kitchen where the temperature is $22^{\circ} \mathrm{C}$. What power is needed to operate this refrigerator}
\text{in order to extract from it $89 \mathrm{MJ}$ of heat in one hour?}
\text{A) $1.8 \mathrm{~kW}$}
\text{B) $2.0 \mathrm{~kW}$}
\text{C) $1.5 \mathrm{~kW}$}
\text{D) $2.9 \mathrm{~kW}$}
\text{E) $1.0 \mathrm{~kW}$}
\text{A Carnot heat engine has an efficiency of 0.350 . If the engine is run in reverse to perform as }
\text{a refrigerator, what is this refrigerator's coefficient of performance?}
\text{A) 1.63}
\text{B) 0.650}
\text{C) 2.15}
\text{D) 0.534}
\text{E) 1.86}
\text{A Carnot heat engine has an efficiency of 0.350 . If the engine is run in reverse to perform as }
\text{a refrigerator, what is this refrigerator's coefficient of performance?}
\text{for an engine:}
\epsilon=1-\frac{T_L}{T_H}
\Rightarrow
\frac{T_H}{T_L}=\frac{1}{1-\epsilon}
\text{For a refregirator:}
\kappa=\frac{T_L}{T_H-T_L}=\displaystyle \frac{1}{\displaystyle \frac{T_H}{T_L}-1}=\frac{1}{\displaystyle \frac{1}{1-\epsilon}-1}=\frac{1-\epsilon}{\epsilon}
\kappa=\frac{1-0.65}{0.35}=1.86
\text{A Carnot engine whose hot reservoir temperature is $400^{\circ} \mathrm{C}$ has a thermal efficiency of $40 \%$.}
\text{By how many degrees should we lower the temperature of the cold reservoir to increase the engine}
\text{efficiency to $60 \%$ ?}
\text{A) $135^{\circ} \mathrm{C}$}
\text{B) $105^{\circ} \mathrm{C}$}
\text{C) $215^{\circ} \mathrm{C}$}
\text{D) $119^{\circ} \mathrm{C}$}
\text{E) $171^{\circ} \mathrm{C}$}
\text{A Carnot engine whose hot reservoir temperature is $400^{\circ} \mathrm{C}$ has a thermal efficiency of $40 \%$.}
\text{By how many degrees should we lower the temperature of the cold reservoir to increase the engine}
\text{efficiency to $60 \%$ ?}
\varepsilon_{\mathrm{c}}=\frac{\mathrm{T}_{\mathrm{H}}-\mathrm{T}_{\mathrm{L}}}{\mathrm{T}_{\mathrm{H}}} \Rightarrow \mathrm{T}_{\mathrm{L}}=\mathrm{T}_{\mathrm{H}}\left(1-\varepsilon_{\mathrm{c}}\right)=673(1-0.4)=403.8 \mathrm{~K}
\text{New lower temperature $T_L'$ for $\varepsilon_{\mathrm{c}}=0.6$}
\begin{aligned}
& \mathrm{T}_{\mathrm{L}}^{\prime}=673(1-0.6)=269.2 K\\
& \Delta \mathrm{T}_{\mathrm{L}}=\mathrm{T}_{\mathrm{L}}-\mathrm{T}_{\mathrm{L}}^{\prime}=403.8-269.2=134.6 \mathrm{C}
\end{aligned}
\text{Additional problems}
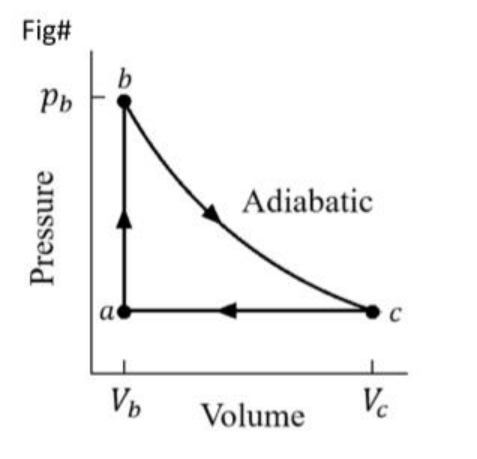
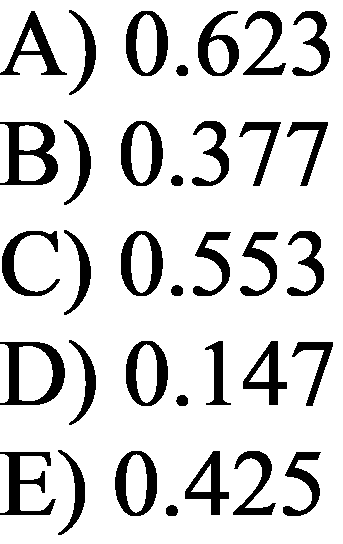
\text{The operation of a heat engine is represented by the cycle shown in the P-V diagram in Figure 4,}
\text{where $V_a=1.00 \mathrm{~L}, V_c=8.00 \mathrm{~L}, p_a=0.313 \mathrm{~atm}$ and $p_b=10.0 \mathrm{~atm}$.}
\text{The working substance is an ideal monatomic ideal gas. What is the efficiency of the engine?}

Q_H
Q_L
\Delta E=0=Q-W
Q=W
Q_H+Q_L=W
\epsilon=\frac{W}{Q_H}=\frac{Q_L+Q_H}{Q_H}={1+\frac{Q_L}{Q_H}}
\text{efficiency=What we get/What we inject}
\epsilon=1+\frac{n c_p \Delta T_{ca}}{nc_v \Delta T_{ab}}=1+{\gamma}\frac{\Delta T_{ca}}{ \Delta T_{ab}}
\epsilon=1+{\gamma}\frac{\Delta T_{ca}}{ \Delta T_{ab}}=1+{\gamma}\frac{P_a(V_a-V_c)}{V_a(P_b-P_a)}
\epsilon=1+{\gamma}\frac{V_a(P_b-P_a)}{P_a(V_a-V_c)}=1+{5/3}\frac{0.313\times(1-8)}{1\times(10-0.313)}=0.62
(T=\frac{PV}{nR})
\text{The operation of a heat engine is represented by the cycle shown in the P-V diagram in Figure 4,}
\text{where $V_a=1.00 \mathrm{~L}, V_c=8.00 \mathrm{~L}, p_a=0.313 \mathrm{~atm}$ and $p_b=10.0 \mathrm{~atm}$.}
\text{The working substance is an ideal monatomic ideal gas. What is the efficiency of the engine?}
Chapter 20
By smstry
Chapter 20
- 517



