\text{Chapter 5}
\text{Chapter 5}
\text{Chapter 5}
\text{Chapter 5}
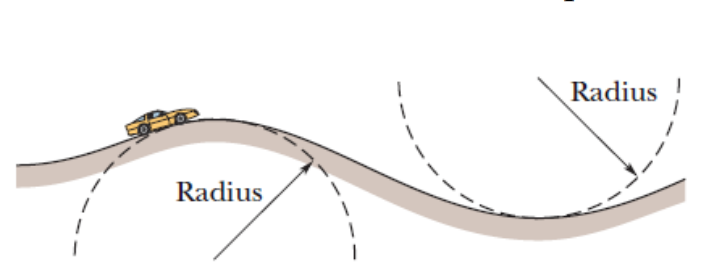
\text{In Figure 9, a car is driven at constant speed over a circular hill and then into a circular valley}
\text{with the same radius. At the top of the hill, the normal force on the driver from the car seat is}
\text{ zero. The driver's mass is $80.0 \mathrm{~kg}$. What is the magnitude of the normal force on the driver }
\text{from the seat when the car passes through the bottom of the valley?}
\textcolor{black}{\text{A) $1.57 \times 10^3 \mathrm{~N}$}}\\
\text{B) $1.01 \times 10^3 \mathrm{~N}$}\\
\text{C) $1.17 \times 10^3 \mathrm{~N}$}\\
\text{D) $2.81 \times 10^3 \mathrm{~N}$}\\
\text{E) $2.22 \times 10^3 \mathrm{~N}$}

\sum \vec{F}=m\vec{a}
m\vec{g}+\vec{F}_N=m\vec{a}
\text{Let us project the eq. on the y-axis on the hill}
-m{g}+{F}_N^\text{hill}=-m{a}_n
\displaystyle {F}_N^\text{hill}=-m\frac{v^2}{R}+mg
\text{Let us project the eq. on the y-axis on the valley}
-m{g}+{F}_N^\text{valley}=m{a}_n
\displaystyle {F}_N^\text{valley}=m\frac{v^2}{R}+mg
\text{we sum the two equations to get:}
\displaystyle {F}_N^\text{valley}+ {F}_N^\text{hill}=2mg
\displaystyle {F}_N^\text{valley}=2mg=2\times 80\times9.8=1.57 \times 10^3 N
\text{since }F_N^\text{hill}=0,
\vec{a}_n
\vec{a}_n
\text{In Figure 9, a car is driven at constant speed over a circular hill and then into a circular valley}
\text{with the same radius. At the top of the hill, the normal force on the driver from the car seat is}
\text{ zero. The driver's mass is $80.0 \mathrm{~kg}$. What is the magnitude of the normal force on the driver }
\text{from the seat when the car passes through the bottom of the valley?}
\text{Answer A}
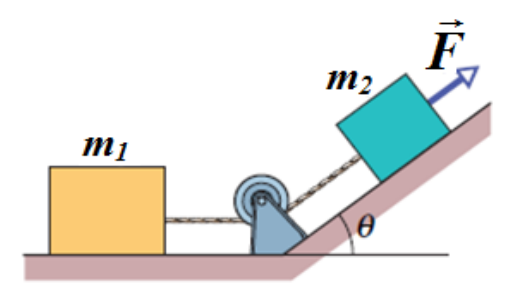
\text{In Figure 6, a force $\overrightarrow{\mathrm{F}}$ of magnitude $12 \mathrm{~N}$ is applied to a box of mass $m_2=1.0 \mathrm{~kg}$. The force is }
\text{directed up a plane tilted by $\theta=37^{\circ}$. The box is connected by a cord to a second box of mass}
\text{$m_1=3.0 \mathrm{~kg}$ on the floor. The floor, plane, and pulley are frictionless, and the masses of the }
\text{pulley and cord are negligible. What is the tension in the cord?}

\text{Mass }m_1:
\vec{T}_1+m_1\vec{g}+\vec{F}_N=m_1 \vec{a}_1
\text{Project on x-axis:}
\displaystyle {T}_1=m_1 {a_1}
\text{Mass }m_2:
\vec{T}_2+m_2\vec{g}+\vec{F}_N+\vec{F}=m_2 \vec{a}_2
\text{Project on x-axis (incline):}
\displaystyle -{T}_2-m_2g \cos (90^0-\theta)+F=m_2 {a}_2
\text{same \textcolor{red}{massless} corde}\Rightarrow T_1=T_2
\text{the two masses move together}\Rightarrow a_1=a_2
\text{\textcircled{A}}
\text{\textcircled{B}}
\text{By substructing the two eq. $m_2$\textcircled{A}-$m_1$\textcircled{B}, we get:}
\displaystyle T=4.6 N
\vec{T}_1
\vec{T}_2
m_1 \vec{g}
m_2 \vec{g}
\vec{F}_N
\vec{F}_N
\text{In Figure 6, a force $\overrightarrow{\mathrm{F}}$ of magnitude $12 \mathrm{~N}$ is applied to a box of mass $m_2=1.0 \mathrm{~kg}$. The force is }
\text{directed up a plane tilted by $\theta=37^{\circ}$. The box is connected by a cord to a second box of mass}
\text{$m_1=3.0 \mathrm{~kg}$ on the floor. The floor, plane, and pulley are frictionless, and the masses of the }
\text{pulley and cord are negligible. What is the tension in the cord?}
\text{(we will note it just $a$)}
\text{ eq. \textcircled{A}+ eq. \textcircled{B}, leads to}
\displaystyle F-m_2g \cos (90^0-\theta)=(m_1+m_2) {a}
\displaystyle a=\frac{F-m_2g \sin\theta}{m_1+m_2 }
\text{using \textcircled{A} we get}
\displaystyle T=\frac{m_1}{m_1+m_2 }(F-m_2g \sin\theta)
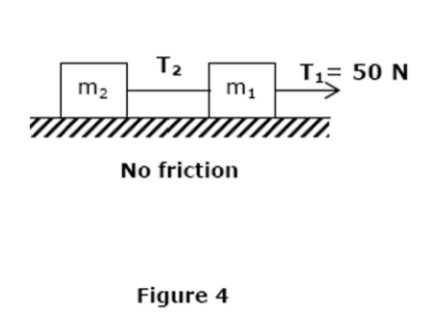
\text{Two masses $\mathrm{m}_1=2.0 \mathrm{~kg}$ and $\mathrm{m}_2=3.0 \mathrm{~kg}$ are connected as shown in Fig 4.}
\text{ Find the tension $\mathrm{T}_2$ if the tension $\mathrm{T}_1=$ $50.0 \mathrm{~N}$.}
\text{A) zero}\\
\text{B) $50.0 \mathrm{~N}$}\\
\text{C) $20.0 \mathrm{~N}$}\\
\text{D) $30.0 \mathrm{~N}$}\\
\text{E) $10.0 \mathrm{~N}$}

\text{On $m_2$}
\vec{T}_2+m_2\vec{g}+\vec{N}=m_2\vec{a}
\text{We project on x-axis}
{T}_2=m_2{a}
\text{On $m_1$}
\vec{T}_1=(m_1+m_2)\vec{a}
\text{We project on x-axis}
{T}_1=(m_1+m_2){a}
\text{because $T_1$ is pulling both masses (no need to plot $\vec{N}$ and m$\vec{g}$)}
\Rightarrow
\displaystyle a=\frac{{T}_1}{(m_1+m_2)}
\Rightarrow
\displaystyle T_2=\frac{m_2{T}_1}{(m_1+m_2)}=30\mathrm{~N}
\text{Two masses $\mathrm{m}_1=2.0 \mathrm{~kg}$ and $\mathrm{m}_2=3.0 \mathrm{~kg}$ are connected as shown in Fig 4.}
\text{ Find the tension $\mathrm{T}_2$ if the tension $\mathrm{T}_1=$ $50.0 \mathrm{~N}$.}
\text{Answer D}

\text{On $m_2$}
\vec{T}_2+m_2\vec{g}+\vec{N}=m_2\vec{a}
\text{We project on x-axis}
{T}_2=m_2{a}
\text{On $m_1$}
\vec{T}_1=(m_1+m_2)\vec{a}
\text{Instead of the above equation, we could have wrote:}
\vec{T}_1+\vec{T}_2=m_1\vec{a}
\Rightarrow
{T}_1-{T}_2=m_1{a}
\text{and then we use the first equation with }T_1
\text{Another way of solving}
\text{Two masses $\mathrm{m}_1=2.0 \mathrm{~kg}$ and $\mathrm{m}_2=3.0 \mathrm{~kg}$ are connected as shown in Fig 4.}
\text{ Find the tension $\mathrm{T}_2$ if the tension $\mathrm{T}_1=$ $50.0 \mathrm{~N}$.}

\begin{align*}
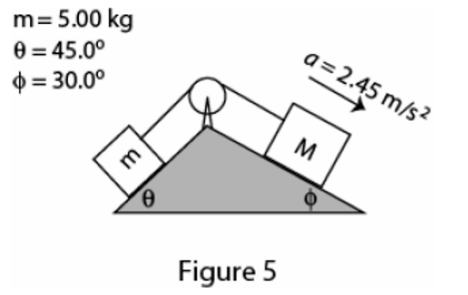
&\text{Two boxes, one of mass } m=5.00\,\mathrm{kg} \text{ and the other with an unknown mass } M,\\
&\text{are connected with a string passing over a massless, frictionless pulley and are placed on}\\
&\text{frictionless planes as shown in Fig.~5. What must be the mass } M \text{ if it goes down the plane}\\
&\text{with an acceleration of } a=2.45\,\mathrm{m\,s^{-2}}\text{?}\\
&\\
&\text{A) }2.50\,\mathrm{kg}\qquad\\
&\text{B) }8.70\,\mathrm{kg}\qquad\\
&\text{C) }13.5\,\mathrm{kg}\qquad\\
&\text{D) }19.1\,\mathrm{kg}\qquad\\
&\text{E) }10.0\,\mathrm{kg}
\end{align*}
\begin{align*}
&\text{Two boxes, one of mass } m=5.00\,\mathrm{kg} \text{ and the other with an unknown mass } M,\\
&\text{are connected with a string passing over a massless, frictionless pulley and are placed on}\\
&\text{frictionless planes as shown in Fig.~5. What must be the mass } M \text{ if it goes down the plane}\\
&\text{with an acceleration of } a=2.45\,\mathrm{m\,s^{-2}}\text{?}\\
\end{align*}

\begin{aligned}
&\text{Along each plane (positive in the direction of motion):}\\[2pt]
&\text{Block }M:\qquad M g\sin\phi - T = M a,\\
&\text{Block }m:\qquad T - m g\sin\theta = m a.\\[4pt]
&\text{Eliminate }T:\quad M g\sin\phi - M a - m g\sin\theta = m a\\
&\Rightarrow\quad M\,(g\sin\phi - a)= m\,(a+g\sin\theta)\\
&\Rightarrow\quad
M=\frac{m\,(a+g\sin\theta)}{g\sin\phi - a}.
\end{aligned}
\begin{aligned}
&\text{With } m=5.00~\mathrm{kg},\ a=2.45~\mathrm{m\,s^{-2}},\ g=9.8~\mathrm{m\,s^{-2}},\\
&\theta=45^\circ\ (\sin\theta=\tfrac{\sqrt2}{2}),\quad
\phi=30^\circ\ (\sin\phi=\tfrac12):\\[4pt]
&M=\frac{5.00\left[\,2.45+9.8\left(\tfrac{\sqrt2}{2}\right)\right]}{9.8\left(\tfrac12\right)-2.45}
=\frac{5.00\,(2.45+6.93)}{4.90-2.45}
=\frac{5.00\times 9.38}{2.45}
\simeq \boxed{19.1~\mathrm{kg}}.
\end{aligned}
\text{Answer D}
m\vec{g}
\vec{N}
\vec{T}
m\vec{g}
\vec{N}
\vec{T}
chapter 5-Phys101
By smstry
chapter 5-Phys101
- 305



