\text{Chapter 18}
\text{Chapter 18}
\text{Chapter 18}
\text{Chapter 18}
\text{Dr. Adel Abbout}
\text{The ends of the two brass and steel rods, each $1.00 \mathrm{~m}$ long; as shown in the Figure 4, are separated}
\text{by $5.00 \mathrm{~mm}$ at $25.0^{\circ} \mathrm{C}$. Assuming that the outside ends of both rods rest firmly against rigid supports,}
\text{at what temperature will the inside ends of the rods just touch?}\\
\text{$\left(\alpha_{\text {steel }}=13.0 \times 10^{-6} /{ }^{\circ} \mathrm{C} ; \alpha_{\text {Brass }}=19.0 \times 10^{-6} / \mathrm{C}^{\circ}\right)$.}


\text{The ends of the two brass and steel rods, each $1.00 \mathrm{~m}$ long; as shown in the Figure 4, are separated}
\text{by $5.00 \mathrm{~mm}$ at $25.0^{\circ} \mathrm{C}$. Assuming that the outside ends of both rods rest firmly against rigid supports,}
\text{at what temperature will the inside ends of the rods just touch?}\\
\text{$\left(\alpha_{\text {steel }}=13.0 \times 10^{-6} /{ }^{\circ} \mathrm{C} ; \alpha_{\text {Brass }}=19.0 \times 10^{-6} / \mathrm{C}^{\circ}\right)$.}

\Delta L_{\text {Brass }}+\Delta L_{\text {Steel }}=d
\Delta T=\frac{d}{L\left(\alpha_{\text {Brass }}+\alpha_{\text {Steel }}\right)}=\frac{5 \times 10^{-3}}{1(19+13) \times 10^{-6}}=156.3
T_f=T_i+\Delta T=25+156.3=181.25^{\circ} \mathrm{C}
L \alpha_\text {Brass }\Delta T+L\alpha_\text {Steel }\Delta T=d
\text{The touching condition is}
\text{What is the change in density of an aluminum cube of mass $200 \mathrm{~g}$ and of edge length $5.0 \mathrm{~cm}$ when }
\text{heated from $10^{\circ} \mathrm{C}$ to $80^{\circ} \mathrm{C}$ (coefficient of linear expansion of aluminum $\left.23 \times 10^{-6} /{ }^{\circ} \mathrm{C}\right)$.}

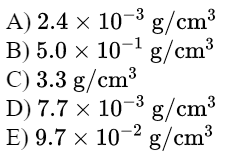
\text{What is the change in density of an aluminum cube of mass $200 \mathrm{~g}$ and of edge length $5.0 \mathrm{~cm}$ when }
\text{heated from $10^{\circ} \mathrm{C}$ to $80^{\circ} \mathrm{C}$ (coefficient of linear expansion of aluminum $\left.23 \times 10^{-6} /{ }^{\circ} \mathrm{C}\right)$.}
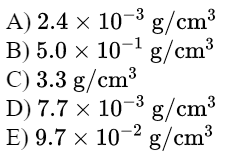

\rho_1=\frac{200}{5^3}=\frac{8}{5} \mathrm{~g} / \mathrm{cm}^3
\rho_2=\frac{200}{(5+\mathrm{L} \alpha \Delta \mathrm{T})^3}=\frac{200}{\left(5+8.05 \times 10^{-3}\right)^3}=1.5922 \mathrm{~g} / \mathrm{cm}^3
\Delta \rho=\left|\rho_2-\rho_1\right|=7.703 \times 10^{-3} \mathrm{~g} / \mathrm{cm}^3
\text{Answer D}
\text{What is the change in density of an aluminum cube of mass $200 \mathrm{~g}$ and of edge length $5.0 \mathrm{~cm}$ when }
\text{heated from $10^{\circ} \mathrm{C}$ to $80^{\circ} \mathrm{C}$ (coefficient of linear expansion of aluminum $\left.23 \times 10^{-6} /{ }^{\circ} \mathrm{C}\right)$.}

\text{More elegant way (not required to be learned for the exam)}
\rho=\frac{m}{V}
\log \rho=\log m -\log V
\text{we do now the derivatives}
\frac{d\rho}{\rho}=\frac{dm}{m}-\frac{dV}{V}
\text{the mass doesn't change, so }dm=0
\text{we change $d\rho$ by $\Delta \rho$}
\frac{\Delta \rho}{\rho}=-\frac{\Delta V}{V}=-3\alpha \Delta T
{\Delta \rho}=-3\alpha \rho\Delta T
\Rightarrow
\Rightarrow
{|\Delta \rho|}=3\times 23\times10^{-6}\times \frac{8}{5}\times70=7.728\times 10^{-3} \text{$\displaystyle \frac{g}{cm^3}$}
\text{Do you want to strengthen your background?}
(\text{Because }\Delta V=V3\alpha \Delta T)
\text{A glass container whose volume is $1.00 \mathrm{~L}$ is completely filled with a liquid at this at $0.00^{\circ} \mathrm{C}$.}
\text{When the filled container is warmed to $55.0^{\circ} \mathrm{C}$, a volume of 8.95 $\mathrm{cm}^3$ of the liquid overflows.}
\text{If the coefficient of linear expansion of glass is $5.67 \times 10^{-6}$ $/ \mathrm{C}^{\circ}$, then find the coefficient of volume}
\text{expansion of the liquid. }
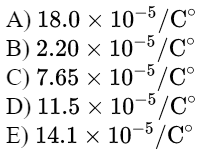
\text{A glass container whose volume is $1.00 \mathrm{~L}$ is completely filled with a liquid at this at $0.00^{\circ} \mathrm{C}$.}
\text{When the filled container is warmed to $55.0^{\circ} \mathrm{C}$, a volume of 8.95 $\mathrm{cm}^3$ of the liquid overflows.}
\text{If the coefficient of linear expansion of glass is $5.67 \times 10^{-6}$ $/ \mathrm{C}^{\circ}$, then find the coefficient of volume}
\text{expansion of the liquid. }
\text{in this problem, the liquid will expand as well as the glass container}
\text{for the glass:}
\Delta V_{\text {glass }}=V_0 \Delta T\beta_{\text {glass }}
\text{for the liquid:}
\Delta V_{\text {liquid }}=V_0 \Delta T\beta_{\text {liquid }}
V'_\text{liquid}-V'_\text{glass}=(V^0_\text{liquid}+\Delta V_\text{liquid})-(V^0_\text{glass}+\Delta V_\text{glass})=(\Delta V_\text{liquid}-\Delta V_\text{glass})
\text{because }V_{glass}=V_\text{liquid}=V^0
V_\text{Overflow}=V_{\text {liquid }}^{\prime}-V_{\text {glass }}^{\prime}=\Delta V_{\text {liquid }}-\Delta V_{\text {glass }}=V_0 \Delta T\left(\beta_{\text {liquid }}-\beta_{\text {glass }}\right)
\beta_{\text {liquid }}=\frac{\Delta V_{\text {overflow }}}{V_0 \times \Delta T}+\beta_{\text {glass }}=\frac{8.95}{10^3 \times 55}+3 \times 5.67 \times 10^{-6}
\beta_{\text {liquid }}=17.97 \times 10^{-5}=18.0 \times 10^{-5} / C^{\circ}
\text{Answer A}
\text{Suppose that on a linear temperature scale $\mathrm{X}$, water boils at $-53.5^{\circ} \mathrm{X}$ and freezes at $-170^{\circ} \mathrm{X}$.}
\text{What is a temperature of $340 \mathrm{~K}$ on the $\mathrm{X}$ scale? $\left(0^{\circ} \mathrm{C}=273 \mathrm{~K}\right)$ }
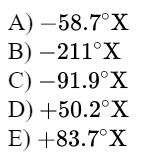
\text{Suppose that on a linear temperature scale $\mathrm{X}$, water boils at $-53.5^{\circ} \mathrm{X}$ and freezes at $-170^{\circ} \mathrm{X}$.}
\text{What is a temperature of $340 \mathrm{~K}$ on the $\mathrm{X}$ scale? $\left(0^{\circ} \mathrm{C}=273 \mathrm{~K}\right)$ }
\text{373 K}
\text{273 K}
\text{$-53.5^0X$}
\text{$-170^0X$}
\text{340 K}
x
\frac{-53.5-x}{-53.5-(-170)}=\frac{373-340}{373-273}
\frac{53.5+x}{-116.5}=\frac{33}{100}
x=-\frac{33}{100}116.5-53.5=-91.8
\text{Answer C}
\text{similar ratios should be equal}
\text{A $150 \mathrm{~g}$ of water at $30.0^{\circ} \mathrm{C}$ is poured over a $60.0 \mathrm{~g}$ cube of ice at a temperature of $-5.00^{\circ} \mathrm{C}$. How many}
\text{gram of ice has melted when the ice-water mixture has reached thermal equilibrium }
\text{specific heat of ice $\mathrm{c}_{\text {ice }}=2220 \mathrm{~J} / \mathrm{kg} . \mathrm{K}$; heat of fusion of ice $\mathrm{L}_{\mathrm{F}}$ $=333 \mathrm{~kJ} / \mathrm{kg}) ?$}

\text{A $150 \mathrm{~g}$ of water at $30.0^{\circ} \mathrm{C}$ is poured over a $60.0 \mathrm{~g}$ cube of ice at a temperature of $5.00^{\circ} \mathrm{C}$. How many}
\text{gram of ice has melted when the ice-water mixture has reached thermal equilibrium }
\text{specific heat of ice $\mathrm{c}_{\text {ice }}=2220 \mathrm{~J} / \mathrm{kg} . \mathrm{K}$; heat of fusion of ice $\mathrm{L}_{\mathrm{F}}$ $=333 \mathrm{~kJ} / \mathrm{kg}) ?$}
\text{If we have a mixture of ice-water at equilibrium then, $T=0$}
\text{water at $30^0$}
\text{ice at $-5^0$}
\text{Water at $0^0$}
\rightarrow
\rightarrow
\rightarrow
Q_1
Q_2
\text{cooling}
\text{melting}
\text{heating}
\text{water at $0^0$}
\text{ice at $0^0$}
Q_\text{water}+Q_\text{ice}=0
m_\text{w}c_\text{w}\Delta T_\text{w}+ (m_{i}c_{i}\Delta T_i+m'_iL_F)=0
\text{heating}
\text{melting}
\text{$m'_i$ is the mass of ice that has melted}
m'=-\frac{m_\text{w}c_\text{w}\Delta T_\text{w}+ m_{i}c_{i}\Delta T_i}{L_F}=-\frac{150\times 4190\times(0-30)+60\times2220\times(0-(-5))}{333\times 10^3}
m'=54.6 \text{ g}
\text{Answer B}
{Q_\text{w}}
(\text{only exchange, no heat is lost})
m_i
m_i
m'_i
\text{One $\mathrm{kg}$ of ice is mixed with one $\mathrm{kg}$ of water at $10.0^{\circ} \mathrm{C}$. When thermal equilibrium is reached, }
\text{the mixture contains total $2.00 \mathrm{~kg}$ of ice at $0.00^{\circ} \mathrm{C}$. Determine the initial temperature of the ice.}
\text{The specific heat of ice $2092 \mathrm{~J} / \mathrm{kg}^{\circ} \mathrm{C}$.}

\text{One $\mathrm{kg}$ of ice is mixed with one $\mathrm{kg}$ of water at $10.0^{\circ} \mathrm{C}$. When thermal equilibrium is reached, }
\text{the mixture contains total $2.00 \mathrm{~kg}$ of ice at $0.00^{\circ} \mathrm{C}$. Determine the initial temperature of the ice.}
\text{The specific heat of ice $2092 \mathrm{~J} / \mathrm{kg}^{\circ} \mathrm{C}$.}
Q_{\text {Water }}+ Q_{\text {ice }}=0
\text{ice at T}
\text{ice at $0^0$}
\text{Heat is not lost and gets only exchanged}
\text{water at $10^0$}
\text{water at $0^0$}
\text{ice at $0^0$}
\rightarrow
\rightarrow
\rightarrow
Q_\text{ice}=m_i c_{i} (0-T)
Q_\text{water}=Q_1+Q_2=m_wc_w(0-10)+m_wL_s
L_s=-L_F=\textcolor{red}{-}333 \text{ kJ/c}
Q_1
Q_2
\text{cooling}
\text{solidification}
\text{heating}
-m_wc_w 10-m_wL_F=m_ic_i T
T=-\frac{m_wc_w 10+m_wL_F}{m_ic_i}=-\frac{1\times10\times4187+333\times 10^3}{1\times 2092}=-179.2 ^0C
\text{Answer A}
\text{A block of mass $125 \mathrm{~g}$ at a temperature of $90.0^{\circ} \mathrm{C}$ is placed in a cup containing 0.326 $\mathrm{kg}$ of water}
\text{ at $20.0^{\circ} \mathrm{C}$. The block and the water reach an equilibrium temperature of $22.4^{\circ} \mathrm{C}$. Neglecting the }
\text{heat capacity of the cup, find the specific heat of the block. }

\text{A block of mass $125 \mathrm{~g}$ at a temperature of $90.0^{\circ} \mathrm{C}$ is placed in a cup containing 0.326 $\mathrm{kg}$ of water}
\text{ at $20.0^{\circ} \mathrm{C}$. The block and the water reach an equilibrium temperature of $22.4^{\circ} \mathrm{C}$. Neglecting the }
\text{heat capacity of the cup, find the specific heat of the block. }
Q_w+Q_B=0
\text{No heat is lost. only exhange of heat accurs.}
m_w c_w\Delta T_w+m_B c_B\Delta T_B=0
c_B=\frac{m_w c_w\Delta T_w}{m_B \Delta T_B}=\frac{m_w \times c_w \times(22.4-20)}{m_B \times(90-22.4)}=\frac{0.326 \times 4187 \times(2.4)}{0.125 \times 67.6}=387.7 \mathrm{~J} / \mathrm{kg} \cdot \mathrm{C}^{\circ}
\text{Find the temperature $T_4$ }
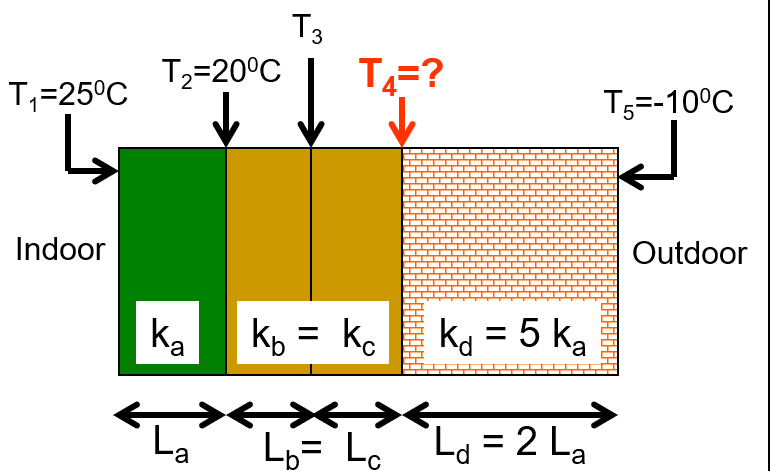
\text{Find the temperature $T_4$ }

\text{In the steady state, the conduction rates through }
\text{all the layers are the same.}
k_a A \frac{T_1-T_2}{L_a}=k_d A \frac{T_4-T_5}{L_d}
k_a A \frac{T_1-T_2}{K_a}=5 L_a A \frac{T_4-T_5}{2 L_a}
\mathrm{T}_1-\mathrm{T}_2=\frac{5}{2}\left(\mathrm{~T}_4-\mathrm{T}_5\right)
25^{\circ} \mathrm{C}-20^{\circ} \mathrm{C}=\frac{5}{2}\left(\mathrm{~T}_4-\left(-10^{\circ} \mathrm{C}\right)\right)
T_4=-8^{\circ} \mathrm{C}
P_a=P_d
\text{{A cubic tank filled with $5.0 \mathrm{~kg}$ of water is insulated from all sides except its top which is covered with }}
\text{a square glass sheet of length $2.0 \mathrm{~m}$ and thickness $3.0 \mathrm{~cm}$. The water is initially at $20^{\circ} \mathrm{C}$. It is exposed }
\text{for 20 seconds to the outside environment where the temperature is $55^{\circ} \mathrm{C}$. Find the change in the }
\text{temperature of water (assume that heat is distributed uniformly in the water). $\left(\mathrm{K}_{\text {glass }}=1.0 \mathrm{~W} / \mathrm{m} . \mathrm{K}\right)$}

\text{{A cubic tank filled with $5.0 \mathrm{~kg}$ of water is insulated from all sides except its top which is covered with }}
\text{a square glass sheet of length $2.0 \mathrm{~m}$ and thickness $3.0 \mathrm{~cm}$. The water is initially at $20^{\circ} \mathrm{C}$. It is exposed }
\text{for 20 seconds to the outside environment where the temperature is $55^{\circ} \mathrm{C}$. Find the change in the }
\text{temperature of water (assume that heat is distributed uniformly in the water). $\left(\mathrm{K}_{\text {glass }}=1.0 \mathrm{~W} / \mathrm{m} . \mathrm{K}\right)$}
\mathrm{Q}=\frac{\mathrm{KA}\left(\mathrm{T}_{\mathrm{H}}-\mathrm{T}_{\mathrm{L}}\right) \mathrm{t}}{\mathrm{L}}=\mathrm{m}_\omega c_\omega \Delta \mathrm{T}
\Delta \mathrm{T}=\frac{\mathrm{KA}\left(\mathrm{T}_{\mathrm{H}}-\mathrm{T}_{\mathrm{L}}\right) \mathrm{t}}{\mathrm{m}_\omega \mathrm{c}_\omega \mathrm{L}}=\frac{(1.0)(4)(55-20)(20)}{3 \times 10^{-2} \times 5.0 \times 4186}
\Rightarrow \Delta \mathrm{T}=4.5^{\circ} \mathrm{C}
\text{Additional problems}
\text{A steel rod is $4.000 \mathrm{~cm}$ in diameter at $35^{\circ} \mathrm{C}$. A brass ring has an inner diameter of $3.992 \mathrm{~cm}$}
\text{at $35^{\circ} \mathrm{C}$. At what common temperature will the brass ring slide onto steal rod?}
\text{$\left[\alpha_{\text {steel }}=11 \times 10^{-6} / \mathrm{K}^{-1}, \alpha_{\text {brass }}=19 \times 10^{-6} / \mathrm{K}^{-1}\right]$ (Ans: $286^{\circ} \mathrm{C}$ )}
\text{when we increase temperature, each length will encrease following the same law}
\Delta L=L\alpha \Delta T
\text{The ring will slide when it will have the same diameter as that of the rod}
D_1=D_2
D_1^0+\Delta D_1=D_2^0+\Delta D_2
\Rightarrow
D_s^0+D_s^0 \alpha_s \Delta T=D_b^0+ D_b^0 \alpha_b \Delta T
\Rightarrow
\Rightarrow
\Delta T=\frac{D_b^0-D_s^0}{(D_s^0 \alpha_s- D_b^0 \alpha_b)}=\frac{3.992-4.000}{(4\times 11-3.992\times19)\times 10^{-6}}
=251^0
T_2=286^0
Chapter 18
By smstry
Chapter 18
- 526



