\text{Review session Major 2}

\text{Dr. Adel Abbout}

\text{Charges $-q$ and $+2 q$ in Figure 3 are located at $x= \pm a$. If $\mathrm{q}=5.00 \mathrm{pC}$ and $a=10.0$ $\mathrm{cm}$,}

\text{find the magnitude of the net electric field at point $\boldsymbol{P}$ due to these charges.}

\cdot

a

2a

-q

x

y

2a

2q

\text{Charges $-q$ and $+2 q$ in Figure 3 are located at $x= \pm a$. If $\mathrm{q}=5.00 \mathrm{pC}$ and $a=10.0$ $\mathrm{cm}$,}

\text{find the magnitude of the net electric field at point $\boldsymbol{P}$ due to these charges.}

\cdot

a

2a

-q

x

y

2a

2q

\text{in this isocel triangle, we have:}

\theta=\tan^{-1}\frac{2a}{a}=63.4^0

E_x=\frac{k \times(2 q+q)}{5 a^2} \times \cos 63.4=\frac{9 \times 10^9 \times 3 \times 5 \times 10^{-12}}{5 \times(0.1)^2} \times \cos 63.4=1.209 \mathrm{~N} / \mathrm{C}

E_y=\frac{k \times(2 q-q)}{5 a^2} \times \sin 63.4=\frac{9 \times 10^9 \times 5 \times 10^{-12}}{5 \times(0.1)^2} \times \sin 63.4=0.805 \mathrm{~N} / \mathrm{C}

E_x=E^1_x+E_x^2=E^1\cos(\theta)+E^2\cos{(-\theta)}

=k\frac{2q}{(\sqrt{5}a)^2}\cos \theta+k\frac{q}{(\sqrt{5}a)^2}\cos\theta

\sqrt{5}a

\theta

\theta

\theta

\theta

\text{An electric dipole is placed in a uniform electric field $\vec{E}=(4000 \hat{i}) N / C$. What is the change }\\

\text{in dipole's potential energy if the initial and the final electric dipole moments $\vec{p}_i$ and $\vec{p}_f$ }

\\ \begin{aligned} & \vec{p}_i=\left(3.72 \times 10^{-30} \hat{i}+4.96 \times 10^{-30} \hat{j}\right) \text { C.m } \\ & \vec{p}_f=\left(6.20 \times 10^{-30} \hat{i}\right) \mathrm{C} . \mathrm{m} \end{aligned}

\text{respectively, are given by}

\text{An electric dipole is placed in a uniform electric field $\vec{E}=(4000 \hat{i}) N / C$. What is the change }\\

\text{in dipole's potential energy if the initial and the final electric dipole moments $\vec{p}_i$ and $\vec{p}_f$ }

\\ \begin{aligned} & \vec{p}_i=\left(3.72 \times 10^{-30} \hat{i}+4.96 \times 10^{-30} \hat{j}\right) \text { C.m } \\ & \vec{p}_f=\left(6.20 \times 10^{-30} \hat{i}\right) \mathrm{C} . \mathrm{m} \end{aligned}

\text{respectively, are given by}

\begin{aligned} U & =-\vec{P} \cdot \vec{E} \\ \Delta U & =U_f-U_i=\left(-\vec{P}_f \cdot \vec{E} \right)-\left(-\vec{P}_i \cdot \vec{E}\right) \\ & =-\left[3.72 \times 10^{-30} \times 4000\right]+\left[6.2 \times 10^{-30} \times 4000\right] \\ & =+1.488 \times 10^{-26}-2.48 \times 10^{-26}=-9.92 \times 10^{-27} J \end{aligned}

\text{\text{Figure 5 shows, in cross section, two Gaussian spheres and two Gaussian cubes. A positive }}\\

\text{charge +q is placed at the center of inner sphere 'a' and a charge of -q is placed between }

\text{the sphere 'c' and the cube ' $d$ '.Rank the net flux $\Phi$ through the four Gaussian surfaces,}

\text{GREATEST FIRST.}

A) \text{$\Phi_{\mathrm{a}}, \Phi_{\mathrm{b}}$, and $\Phi_{\mathrm{c}}$ tie, $\Phi_{\mathrm{d}}$}

B) \text{$\Phi_{\mathrm{d}}, \Phi_{\mathrm{a}}, \Phi_{\mathrm{b}}, \Phi_{\mathrm{c}}$}

C) \text{$\Phi_{\mathrm{d}}$ than $\Phi_{\mathrm{a}}, \Phi_{\mathrm{b}}$, and $\Phi_{\mathrm{c}}$ tie}

D) \text{$\Phi_{\mathrm{d}}, \Phi_{\mathrm{b}}, \Phi_{\mathrm{c}}, \Phi_{\mathrm{a}}$}

E) \text{$\Phi_{\mathrm{d}}$ and $\Phi_{\mathrm{b}}$ tie, $\Phi_{\mathrm{a}}$ and $\Phi_{\mathrm{c}}$ tie}

\cdot

+q

\cdot

-q

a

b

c

d

\text{\text{Figure 5 shows, in cross section, two Gaussian spheres and two Gaussian cubes. A positive }}\\

\text{charge +q is placed at the center of inner sphere 'a' and a charge of -q is placed between }

\text{the sphere 'c' and the cube ' $d$ '.Rank the net flux $\Phi$ through the four Gaussian surfaces,}

\text{GREATEST FIRST.}

\cdot

+q

\cdot

-q

a

b

c

d

\phi=\frac{q_\text{enc}}{\epsilon_0}

\text{For a, b and c, we have: $q_\text{enc}=+q$}

\text{For d, we have: $q_\text{enc}=+q-q=0$}

\text{Answer A}

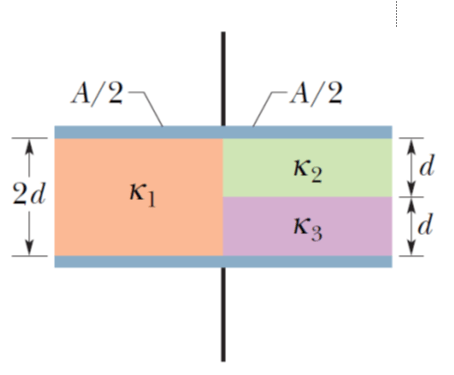
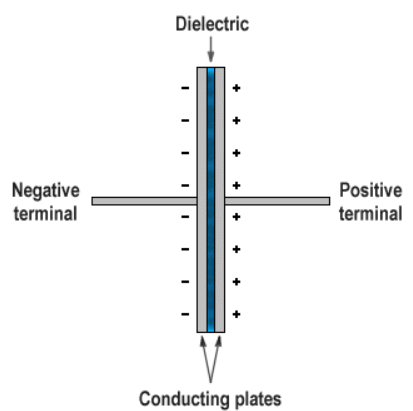
\text{Figure 1 shows a parallel-plate capacitor of plate area $A=10.5 \mathrm{~cm}^2$ and plate separation }

\text{$2 d=7.12 \mathrm{~mm}$. The left half of the gap is filled with material of dielectric constant $\kappa_1=21.0$;}

\text{the top of the right half is filled with material of dielectric constant $\kappa_2=42.0$; the bottom of }

\text{the right half is filled with material of dielectric constant $\kappa_3=$ 58.0. What is the capacitance?}

\text{Figure 1 shows a parallel-plate capacitor of plate area $A=10.5 \mathrm{~cm}^2$ and plate separation }

\text{$2 d=7.12 \mathrm{~mm}$. The left half of the gap is filled with material of dielectric constant $\kappa_1=21.0$;}

\text{the top of the right half is filled with material of dielectric constant $\kappa_2=42.0$; the bottom of }

\text{the right half is filled with material of dielectric constant $\kappa_3=$ 58.0. What is the capacitance?}

\kappa_1

\kappa_2

\kappa_3

\text{The equivalent system is: }

A/2

A/2

A/2

\text{Figure 1 shows a parallel-plate capacitor of plate area $A=10.5 \mathrm{~cm}^2$ and plate separation }

\text{$2 d=7.12 \mathrm{~mm}$. The left half of the gap is filled with material of dielectric constant $\kappa_1=21.0$;}

\text{the top of the right half is filled with material of dielectric constant $\kappa_2=42.0$; the bottom of }

\text{the right half is filled with material of dielectric constant $\kappa_3=$ 58.0. What is the capacitance?}

\kappa_1

\kappa_2

\kappa_3

\text{The equivalent system is: }

\text{$C_2$, $C_3$ are in series and their equivalentcapacitor is in parallel with $C_1$}

C_\text{eq}=\frac{\kappa_1\epsilon_0 \frac{A}{2}}{2d}+\frac{\frac{\kappa_2\epsilon_0 A/2}{d} \frac{\kappa_3\epsilon_0 A/2}{d} }{\frac{\kappa_2\epsilon_0 A/2}{d} +\frac{\kappa_3\epsilon_0 A/2}{d} }=\Big(\frac{\kappa_1}{2}+\frac{\kappa_2\kappa_3}{\kappa_2+\kappa_3}\Big)\frac{\epsilon_0 A}{2d} =4.55\times10^{-11}F

A/2

A/2

A/2

\begin{aligned} & \text{Figure 3 shows a pyramid with horizontal square base, $a = 6.00 \, \mathrm{m}$ on each side, and a height,}\\ & \text{$h = 4.00 \, \mathrm{m}$. The pyramid is placed in an upward vertical electric field of magnitude $E = 52.0 \, \mathrm{N/C}$.}\\ & \text{If the pyramid does not include any charge inside, calculate the electric flux, in $\mathrm{N \cdot m^2/C}$,}\\ &\text{through its four slanted (inclined) surfaces.} \end{aligned}

A) +1.87\times10^3\\ B) -1.87\times10^3\\ C) +0.90\times10^3\\ D) -0.90\times10^3\\ E) -3.27\times10^3

a

a

\vec{E}

h

\begin{aligned} & \text{Figure 3 shows a pyramid with horizontal square base, $a = 6.00 \, \mathrm{m}$ on each side, and a height,}\\ & \text{$h = 4.00 \, \mathrm{m}$. The pyramid is placed in an upward vertical electric field of magnitude $E = 52.0 \, \mathrm{N/C}$.}\\ & \text{If the pyramid does not include any charge inside, calculate the electric flux, in $\mathrm{N \cdot m^2/C}$,}\\ &\text{through its four slanted (inclined) surfaces.} \end{aligned}

\phi_\text{tot}=\frac{q_\text{enc}}{\epsilon_0}=0,

\text{No charge inside}

\phi_\text{tot}=\phi_\text{base}+\phi_\text{slanted}=0

\phi_\text{slanted}=-\phi_\text{base}=-\vec{E}\cdot\vec{A}

\phi_\text{slanted}=-\vec{E}\cdot\vec{A}=+E A=52\times 36=1.87\times 10^3 \text{ $N\cdot m^2/C$}

\text{Answer A}

a

a

\vec{E}

h

C

C

C

C

C

C

\text{Figure 8 shows 6 identical capacitors, each with a capacitance of 1.0 $\mu F$. Finf the equivalent}

\text{capacitance $C_{eq}$ between the points A and B.}

A

B

A) 1.5 \mu F\\ B) 2.3 \mu F\\ C) 3.0 \mu F\\ D) 4.4 \mu F\\ E) 4.7 \mu F\\

C

C

C

C

C

C

\text{Figure 8 shows 6 identical capacitors, each with a capacitance of 1.0 $\mu F$. Finf the equivalent}

\text{capacitance $C_{eq}$ between the points A and B.}

A

B

A

A

A

B

C_{eq}= \frac{3 C\times 3C}{3C+ 3C}=1.5 C=1.5\mu F

C

C

C

C

C

\begin{aligned} &\text{A particle with a charge of $5.5 \times 10^{-8} \, \mathrm{C}$ is fixed at the origin. A particle with a charge of} \\ &\text{$-2.3 \times 10^{-8} \, \mathrm{C}$ is moved from $x = 3.5 \, \mathrm{cm}$ on the x-axis to $y = 4.3 \, \mathrm{cm}$ on the y-axis. The}\\ &\text{change in potential energy of the two-particle system is } \end{aligned}

\begin{gathered} \text{A) $+6.0 \times 10^{-5}J$} \\ \text{B) $-3.1 \times 10^{-3}J$} \\ \text{C) $+3.1 \times 10^{-3}J$} \\ \text{D) $-6.0 \times 10^{-5}J$} \\ \end{gathered}

\text{E) $0$} \\

\Delta U=U_f-U_i=k\frac{q_1q_2}{r'_{12}}-k\frac{q_1q_2}{r_{12}}=k{q_1q_2}\Big(\frac{1}{r'_{12}}-\frac{1}{r_{12}}\Big)

=-9\times10^9 \times{5.5\times 10^{-8} \times 2.3\times 10^{-8}} \Big(\frac{1}{4.3\times10^{-2}}-\frac{1}{3.5\times10^{-2}}\Big)

=+6.0\times10^{-5} J

\text{The change in the potential energy is:}

\begin{aligned} &\text{A particle with a charge of $5.5 \times 10^{-8} \, \mathrm{C}$ is fixed at the origin. A particle with a charge of} \\ &\text{$-2.3 \times 10^{-8} \, \mathrm{C}$ is moved from $x = 3.5 \, \mathrm{cm}$ on the x-axis to $y = 4.3 \, \mathrm{cm}$ on the y-axis. The}\\ &\text{change in potential energy of the two-particle system is } \end{aligned}

\cdot

\cdot

\cdot

3.5 \text{ cm}

4.3 \text{ cm}

q_1

q_2

\begin{aligned} & \text{The electric potential $V$ in a region of space is given by }\\ &\hspace{2 cm}V(x,y,z) = A(x^2 - 3y^2 + z^2)&\\ &\text{where $A$ is a constant. If the work done by the field when a $1.50 \, \mu \mathrm{C}$ test charge }\\ &\text{is moved from the point $(x, y, z) = (0 \, \mathrm{m}, 0 \, \mathrm{m}, 0.250 \, \mathrm{m})$ to the origin is $6.00 \times 10^{-5} \, \mathrm{J}$, }\\ &\text{then find the constant $A$.} \end{aligned}

A)\hspace{1mm} 640 \hspace{1mm}V/m^2\\ B)\hspace{1mm} 450 \hspace{1mm}V/m^2\\ C)\hspace{1mm} 523 \hspace{1mm}V/m^2\\ D)\hspace{1mm} 357 \hspace{1mm}V/m^2\\ E)\hspace{1mm} 553 \hspace{1mm}V/m^2

\begin{aligned} & \text{The electric potential $V$ in a region of space is given by }\\ &\hspace{2 cm}V(x,y,z) = A(x^2 - 3y^2 + z^2)&\\ &\text{where $A$ is a constant. If the work done by the field when a $1.50 \, \mu \mathrm{C}$ test charge }\\ &\text{is moved from the point $(x, y, z) = (0 \, \mathrm{m}, 0 \, \mathrm{m}, 0.250 \, \mathrm{m})$ to the origin is $6.00 \times 10^{-5} \, \mathrm{J}$, }\\ &\text{then find the constant $A$.} \end{aligned}

W=-\Delta U=-q\Delta V

\Delta V= 0-A\times 0.25^2=-A\times 0.25^2

A=\frac{W }{q\times0.25^2}=\frac{6.00\times 10^{-5}}{0.25^2\times 1.50\times 10^{-6}}=640\hspace{1mm}V/m^2

\Delta U=q\Delta V

W=-\Delta U

V_f-V_i=-\int_i^f \vec{E}\cdot d\vec{s}

E=\frac{\lambda}{2\pi\epsilon_0 r}

\text{Answer A}