
Deep Learning with Tensorflow:
Achieving Optimal Model Performance
Sahil Singh
Topics of Discussion
- Input Normalisation
- Weight Initialization Strategies
- Loss Functions
- Activation Functions
- Choice of Optimizers
- Dropout
- Optimizer Hyperparamters (learning rate, epochs, etc.)
- Model Hyperparameters (no. of hidden layers, hidden layer size, etc.)
- Batch Normalization
Structure of the Workshop
- Highlighting the problem
- A discussion of the technique that can address the problem
- Implementation in Code
Starting model
A benchmark network in keras.
Dataset: MNIST
No. of hidden layers: 2
No. of hidden units: 10

from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot as plt
import seaborn as sns
(x_train, y_train), (x_test, y_test) = mnist.load_data()
num_classes = 10
# Apply one-hot encoding to the labels
y_train = to_categorical(y_train, num_classes)
y_test = to_categorical(y_test, num_classes)
# Break training data into training and validation sets
(x_train, x_valid) = x_train[:50000], x_train[50000:]
(y_train, y_valid) = y_train[:50000], y_train[50000:]
# Model definition
model = Sequential()
model.add(Flatten(input_shape=(28,28)))
# Model hyperparameter
num_hidden_layers = 2
num_hidden_units = 10
for _ in range(num_hidden_layers):
model.add(Dense(num_hidden_units))
model.add(Activation('relu'))
# Output Layer
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# Set optimization hyperparameters
batch_size = 256
epochs = 10
model.compile(
optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(
x_train, y_train,
epochs=epochs,
batch_size=batch_size,
validation_data=(x_valid, y_valid),
verbose=2)
accuracy_score = model.evaluate(
x_test, y_test, batch_size=128)
print(f'\nTest accuracy: {accuracy_score[1]:>5.3f}')
Epoch 1/10
1s - loss: 2.8814 - acc: 0.2122 - val_loss: 1.9508 - val_acc: 0.2677
Epoch 2/10
0s - loss: 1.9028 - acc: 0.2714 - val_loss: 1.8804 - val_acc: 0.2859
...
...
...
Epoch 10/10
0s - loss: 0.9046 - acc: 0.6434 - val_loss: 0.8798 - val_acc: 0.6495
5632/10000 [===============>..............] - ETA: 0s
Test accuracy: 0.648Model Evaluation
Input Normalisation
Rule of Thumb
Input values and activations should be small and not come from highly variable distributions.
Different units for features
- Features could be measured in different units - Kms and Kgs
- Normalization makes inputs uniform for all feature representations
- Large values lead to saturating gradients.
- Results in efficient training
- Min-Max Normalization and Z-Score Normalization
Min-Max Normalization
A' = \left(\frac{A - \min{A}}{\max{A} - \min{A}}\right) * (D - C) + C
A′=(maxA−minAA−minA)∗(D−C)+C
A is the overall range of values. [C, D] is the interval that we want to map to.
For the range [0, 1], The formula becomes:
A' = \left(\frac{A - \min{A}}{\max{A} - \min{A}}\right)
A′=(maxA−minAA−minA)
Weight Initialization Strategies
The problem with improper weights
Strategies for initialization
- All zeros
- Sampling Normal Distribution ~ (0, 1)
- Sampling Normal Distribution ~ (0, 0.1)
- Xavier Initialization
- He Initialization
All Zeros
- Never do this!
- All neurons output similar activations
- Similar gradients during backpropagation
- We need to break asymmetry between inputs
Sampling Normal Distribution ~ (0,1)
- Can result in the weighted inputs being large
- Saturating Neurons
tf.truncated_normal(shape=(INPUT, OUTPUT), mean=0, stddev=1)Sampling Normal Distribution ~ (0,0.1)
- Weights concentrated near 0
- Efficient learning
- Can be used as the go-to strategy
tf.truncated_normal(shape=(INPUT, OUTPUT), mean=0, stddev=0.1)Xavier Initialization
- Glorot & Bengio (2010)
- Sample Normal Distribution ~ (0, 1/N)
- Works well in many cases
- Not ideal for ReLu activations
W = tf.get_variable("W", shape=[INPUT, OUTPUT], initializer=tf.contrib.layers.xavier_initializer())He Initialization
- Sample Normal Distribution ~ (0, 2/N)
W = tf.get_variable("W", shape=[INPUT, OUTPUT], initializer=tf.contrib.layers.variance_scaling_initializer())
Activation Functions

Activation Functions
Sigmoid
- The problem of vanishing gradient
- Output is not zero-centered
- Not a good choice for hidden layers
- Almost always applied at the final output layer (Binary Classification)
Activation Functions
Tanh
- The problem of vanishing gradient remains
- Output is zero-centered
- Not the ideal choice for hidden layers
- In practice, performs better than Sigmoid
Activation Functions
Rectified Linear Units (ReLu)
- Solves the problem of vanishing gradient
- Standard non-linearity for hidden layers
- Can suffer from 'dead' hidden units.
Batch Normalization
Batch Normalization
- Normalizing inputs to all the layers of a network
- Normalization using mean and variance of the current mini-batch
- Inference happens using population mean and variance
Batch Normalization
- Network trains slower
- Helps with the problem of vanishing gradients
- Added job of regularizing the model
- Leads to faster convergence to optimal accuracy.
- Allows higher learning rates, faster training.
- Allows building much deeper networks.
Before Batch Normalization

After Batch Normalization

Dropout
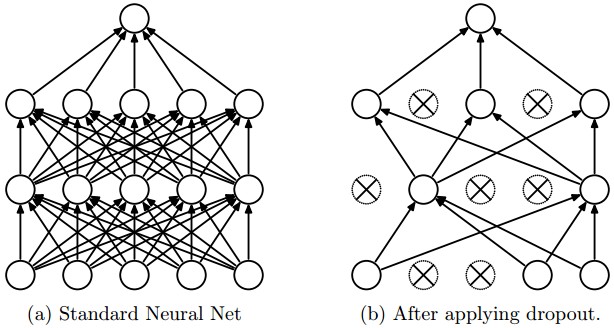
Image Source: http://http://cs231n.github.io
Dropout
- Main job is to prevent overfitting
- Works extremely well.
- Increases training time.
- Requires hyperparameter tuning (keep probability)
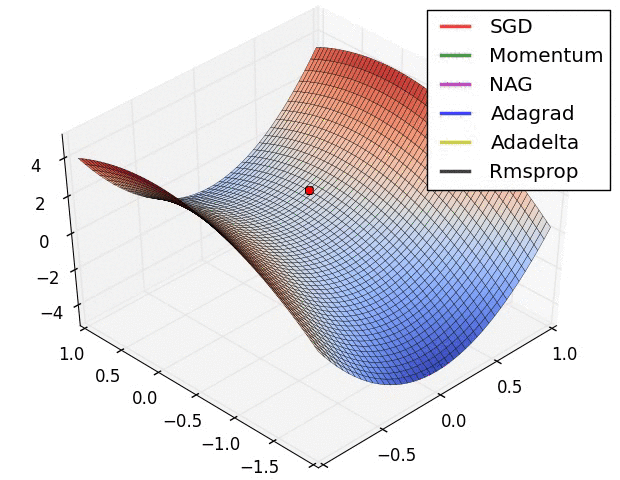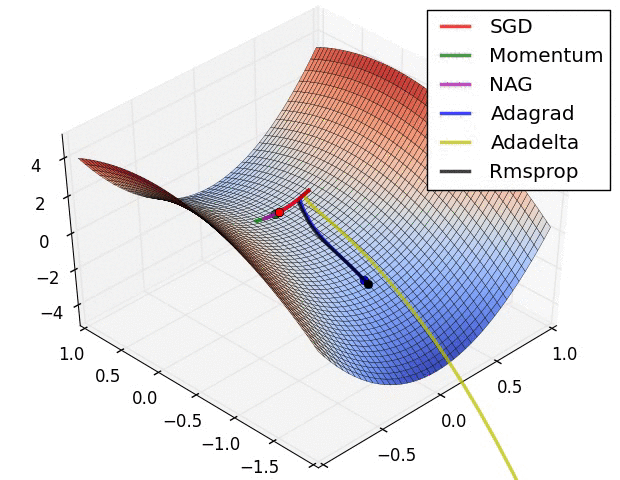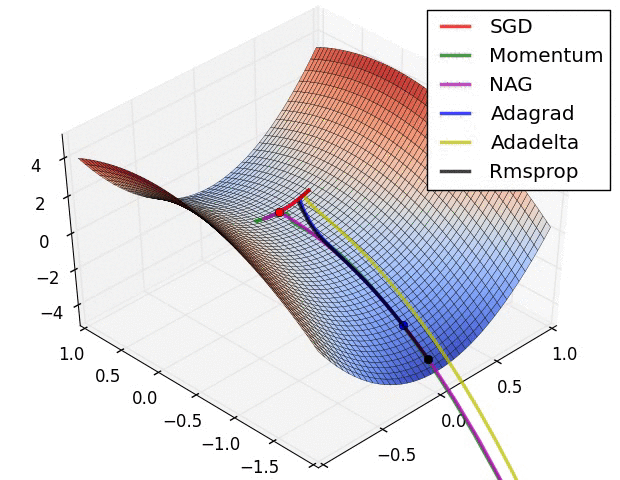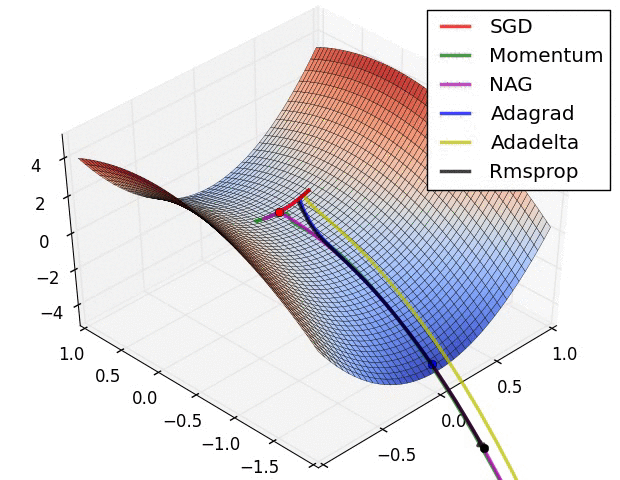
Choice of optimizers
- Optimal Learning rate
- Why use the same learning rate for every parameter?
- Escape sub-optimal local minima
- Deal with Saddle points
Choice of optimizers
- GradientDescentOptimizer
- Momentum Optimizer
- AdagradOptimizer
- AdamOptimizer
Gradient Descent Optimizer
- The baseline optimizer
- Essentially used as the Stochastic Gradient Descent optimizer
- Only parameter to tune is learning rate
Momentum Optimizer
- Softens the update oscillations in irrelevant directions
- Adds a fraction of the past step update to the current one
- Parameter vector builds up velocity in the direction of consistent gradients
- Can overshoot minima - Use Nesterov Momentum
AdaGrad Optimizer
- Uses different learning rate for every parameter based on past gradients
- Parameters with high gradients will have learning rate reduced
- Weights with small/infrequent updates have their learning rates increased
- Disadvantage - Learning rates always decreasing
- Can lead to situation where no learning happens
- Rectified by AdaDelta Optimizer
Adam Optimizer
- Combines the best of AdaGrad and RMSProp
- AdaGrad works well for Sparse features and gradients
- Best performing optimizer
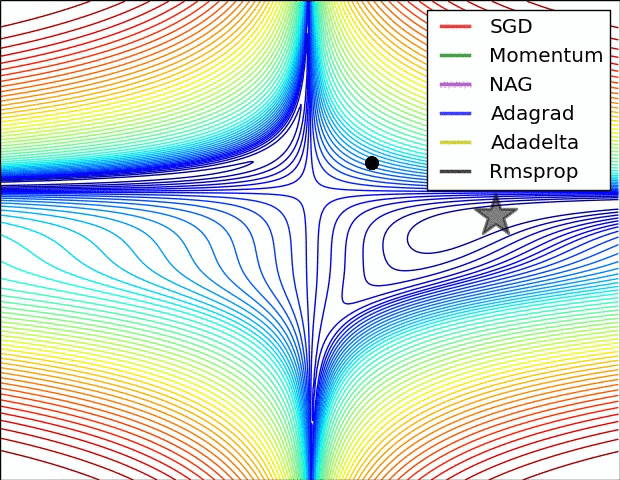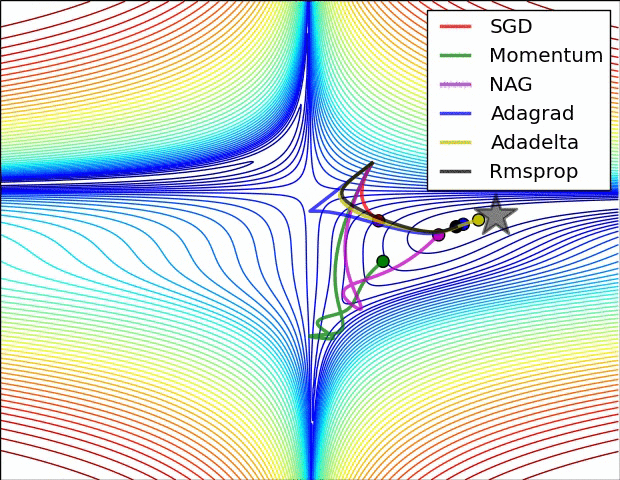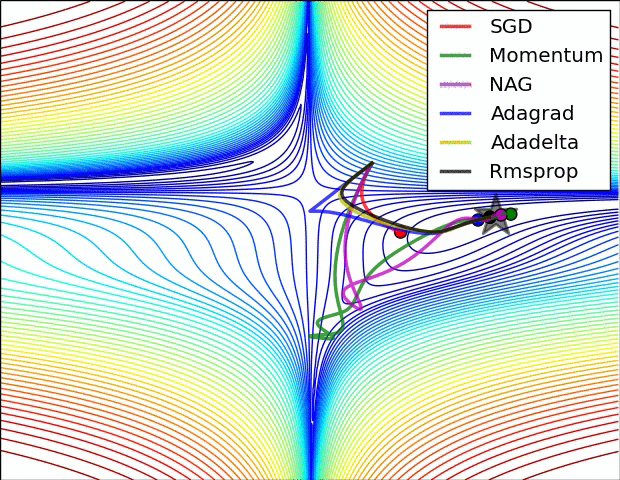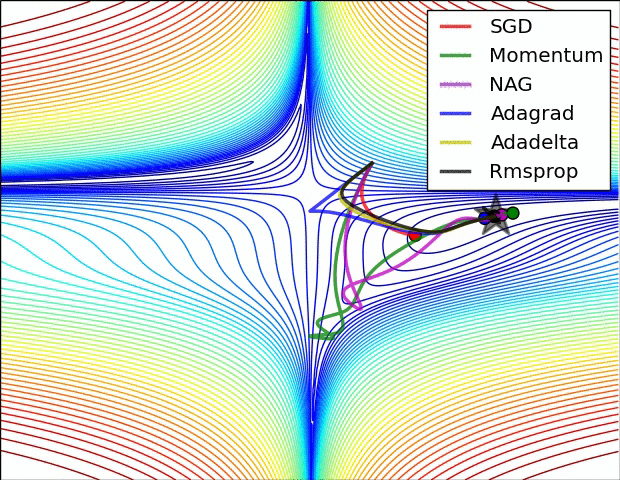
Hyperparameters
Optimizer Hyperparameters
- Learning Rate
- Momentum
- Mini-batch size
- Number of Epochs
Learning Rate
- The most important hyperparameter to tune.
- Larger values can make the model very unstable.
- Lower values take too long to converge.
Batch Size
Small
- Good for training.
- Smaller updates and longer training leads to lower overall error.
- Lower learning rates and more epochs means longer training times.
- Need to compensate with lower learning rates and more epochs
- Low memory usage.
Batch Size
Large
- High memory consumption.
- Lower number of weight updates will not let the network train effectively
- Faster training.
Epochs
- Need to stop training before network starts overfitting
- Use large values and checkpoint model training
Model Hyperparameters
- Number of Hidden Layers
- Number of Hidden Units
Number of Hidden Layers
- Helps increase the representative power of the model
- Increasing helps capture hierarchical structures better - e.g. CNNs
Number of Hidden Units
- Should be as large as possible - more parameters to tune
- Same size for all layers works better in practice
- Overcomplete layers better than undercomplete layers.
Batch Normalization
Deep Learning with Tensorflow
By sngsahil
Deep Learning with Tensorflow
- 1,708
