Applied Algorithms
Chris Hung (Rocket & Optimization)
Content
- Projects and researches
- Kibo RPC
- Project Management
- Searching methods in research
- Control Theory
- Kalman filter
- LQG
- Taylor polynomial approach to optimal guidance
- Fourier transform
- Path planning
- A* family
- D* family
- RRT*
Kibo RPC
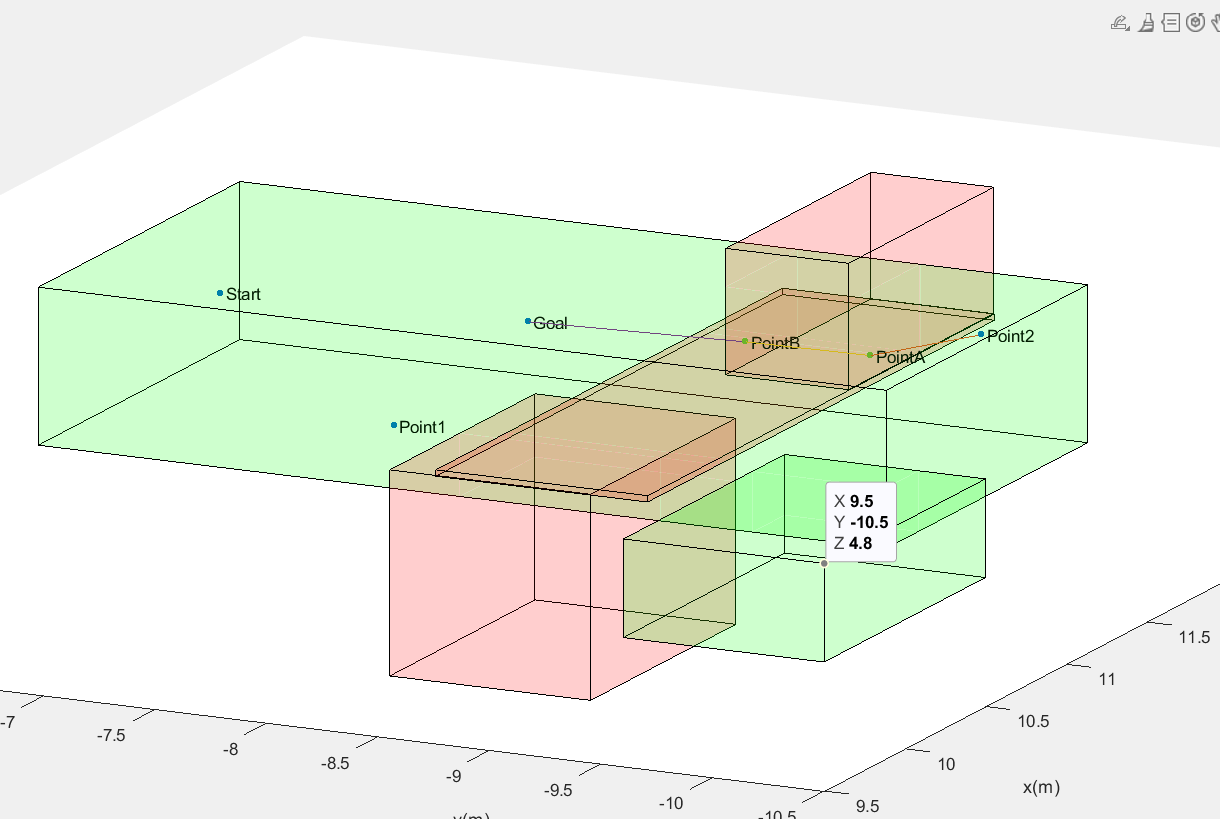


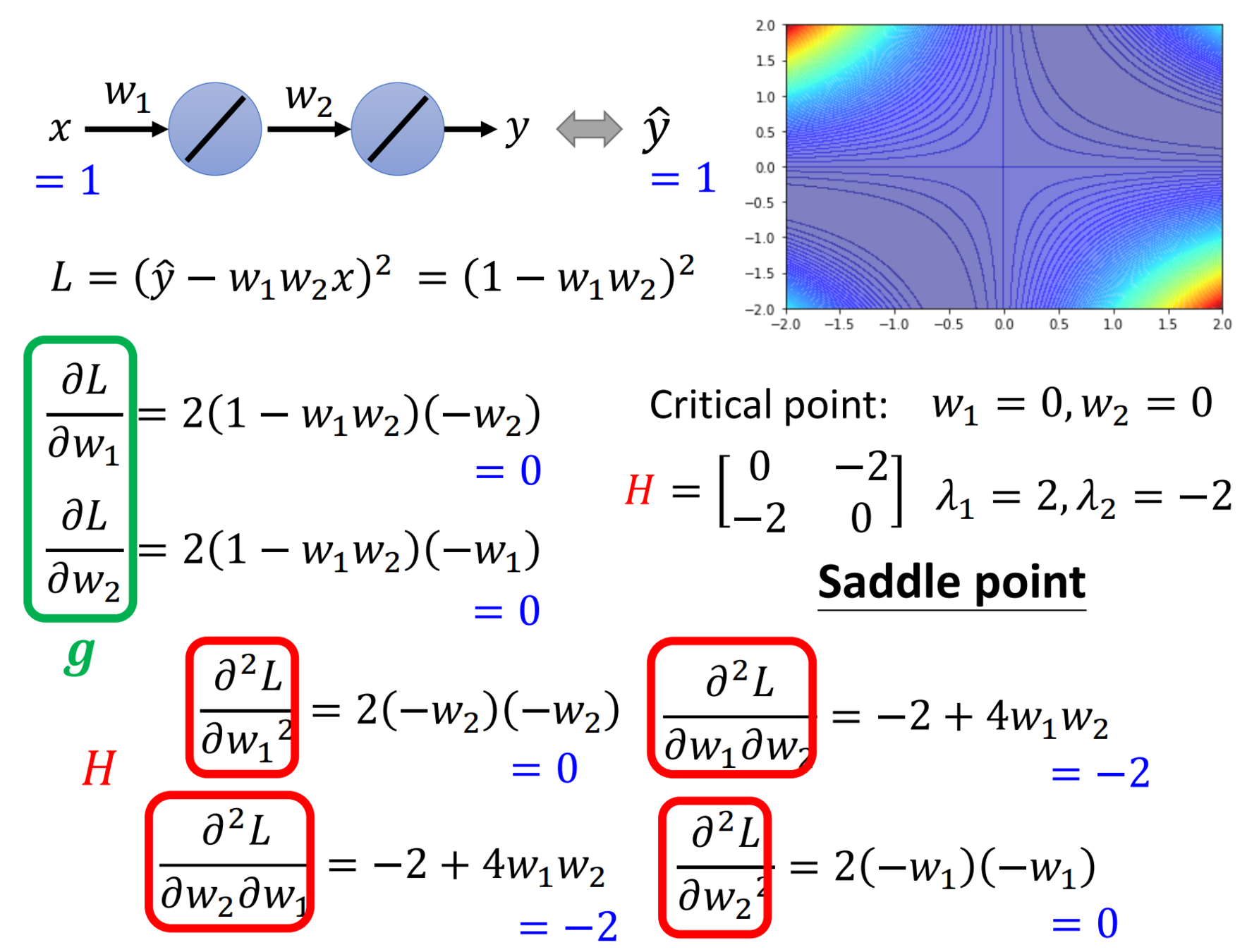
Partial Derivative and Eigen Method
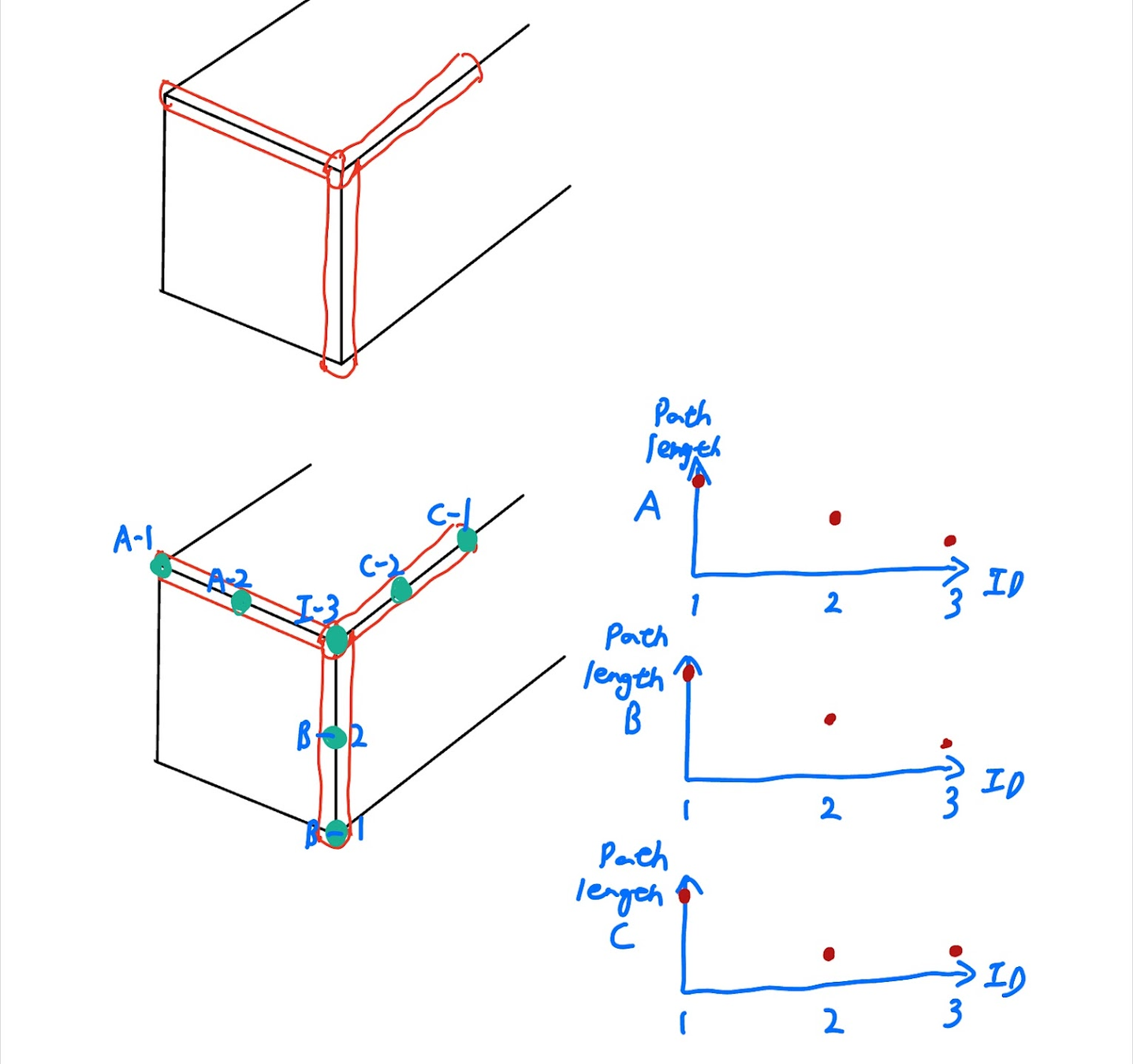
void DecideSearchingMethod()
{
if(linear())
Binary_Search();
else
Ternary_Search();
}- The robot is considered a point mass.
- The amplitude of the disturbance is a gaussian distribution
- Thus, we decide the distance to the edge by disturbance
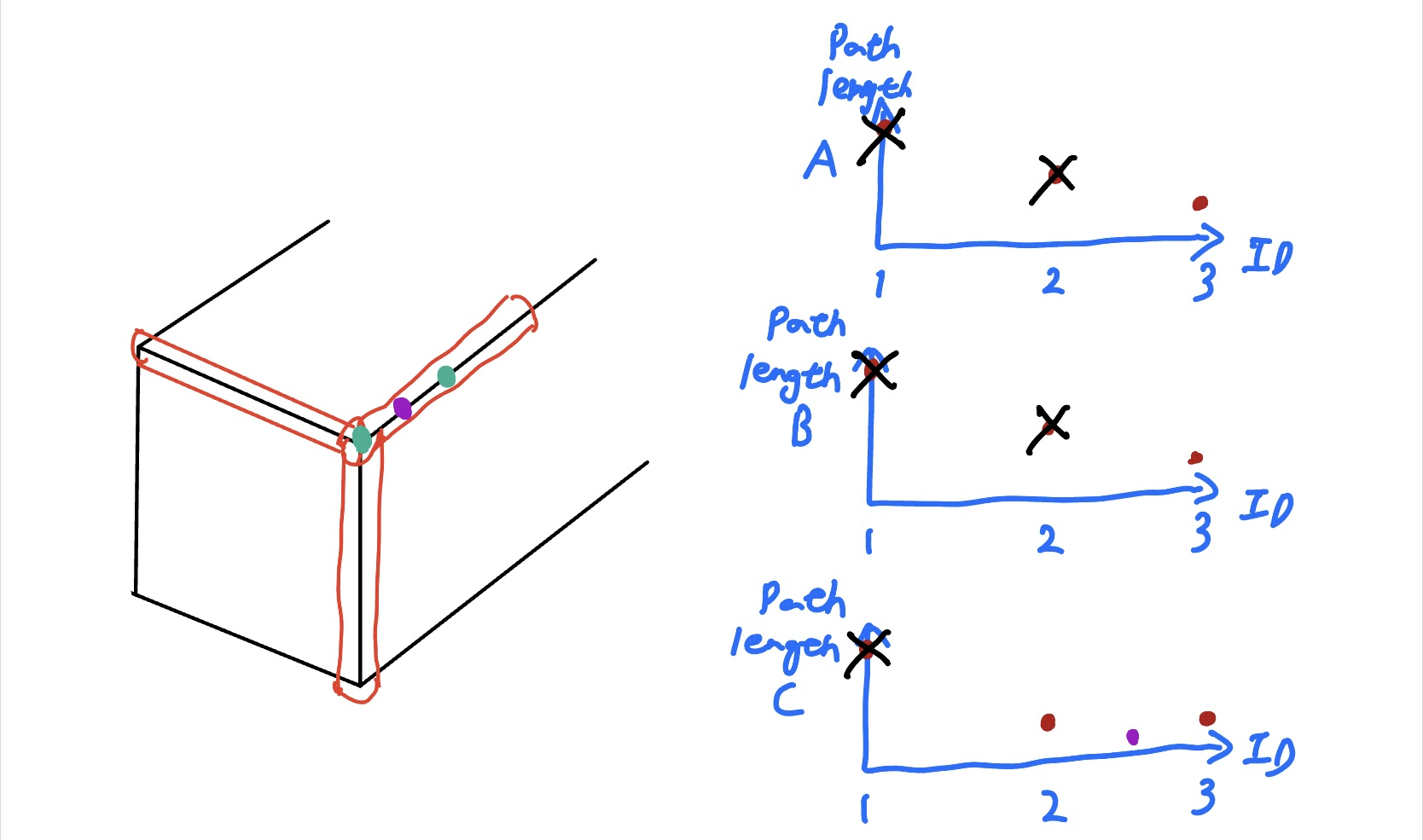
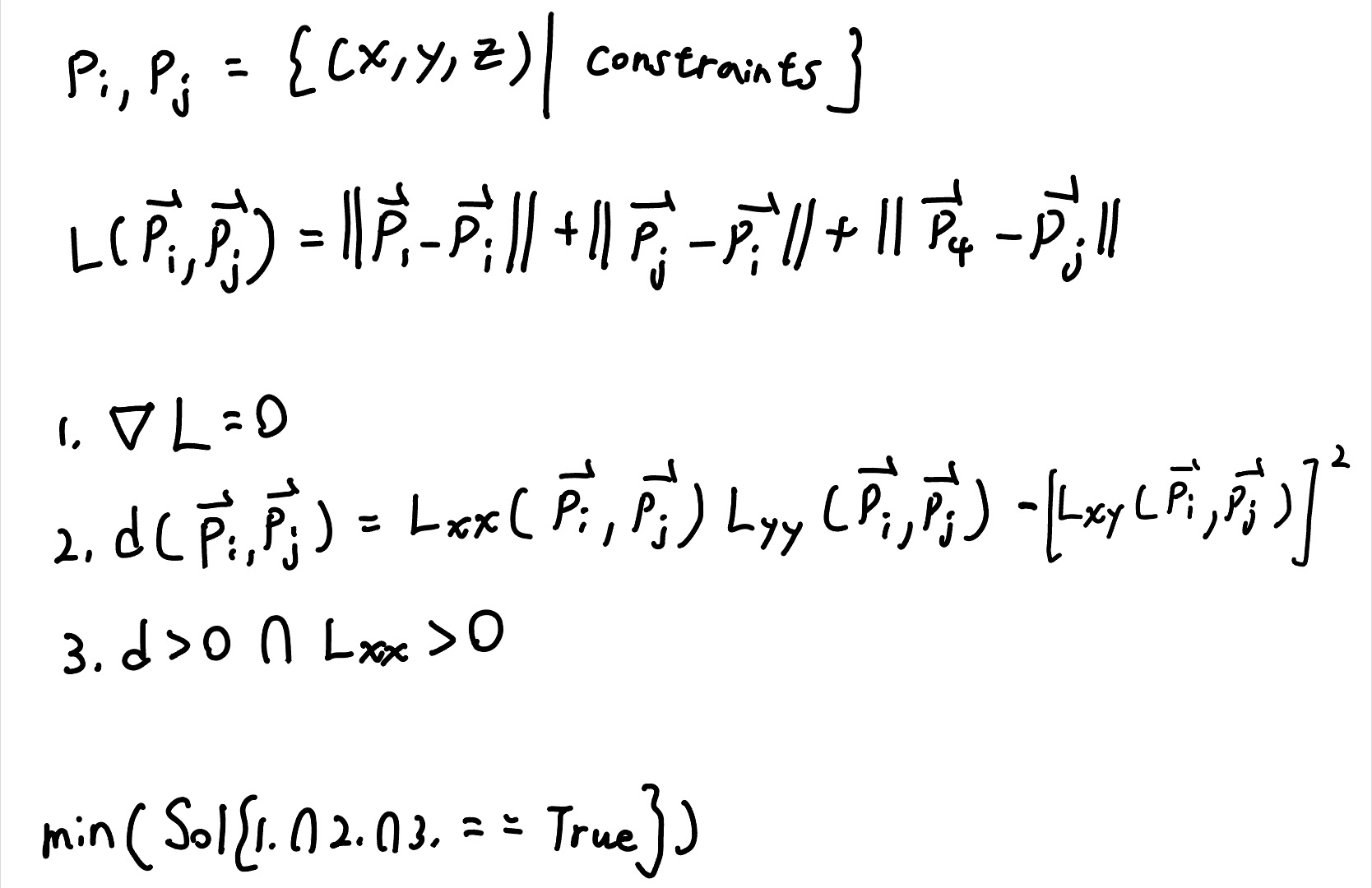
7*7 Hessian Matrix

Path Verification
public boolean PathAvoidKOZ(Point begin, Point end)
{
for(int i=0;i<KOZ_MAX.size();i++)
{
if((begin.getX()>=KOZ_MIN.get(i).getX()&&begin.getX()<=KOZ_MAX.get(i).getX())||end.getX()<=KOZ_MAX.get(i).getX()&&end.getX()>=KOZ_MIN.get(i).getX())
if((begin.getY()>=KOZ_MIN.get(i).getY()&&begin.getY()<=KOZ_MAX.get(i).getY())||end.getY()<=KOZ_MAX.get(i).getY()&&end.getY()>=KOZ_MIN.get(i).getY())
if((begin.getZ()>=KOZ_MIN.get(i).getZ()&&begin.getZ()<=KOZ_MAX.get(i).getZ())||end.getZ()<=KOZ_MAX.get(i).getZ()&&end.getZ()>=KOZ_MIN.get(i).getZ())
return true;
}
return false;
}
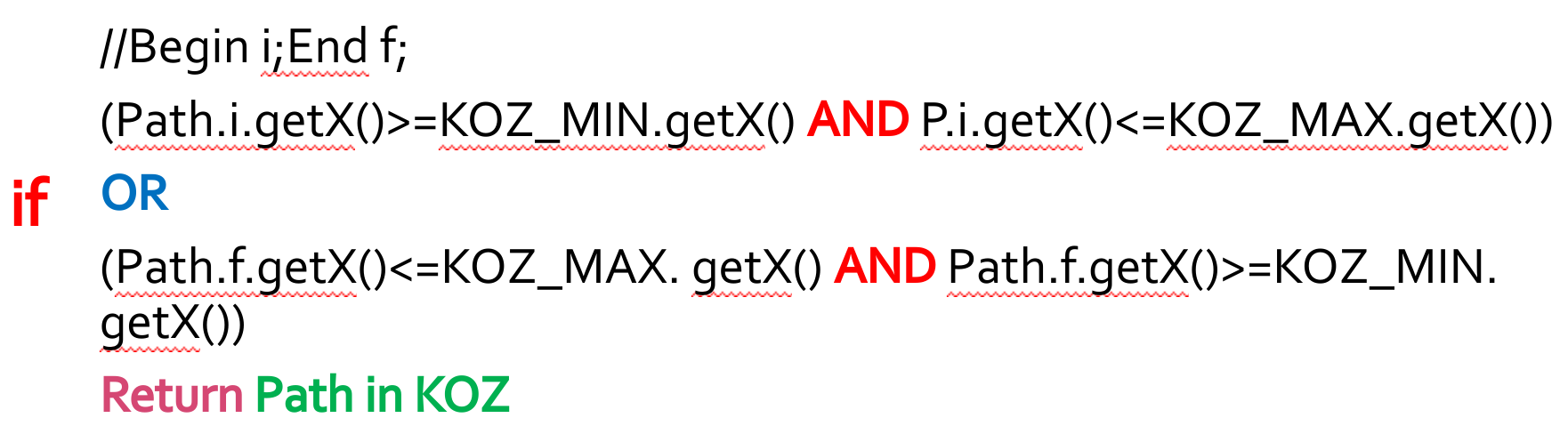
Project Management
Topological sort, PERT
Topological Sort
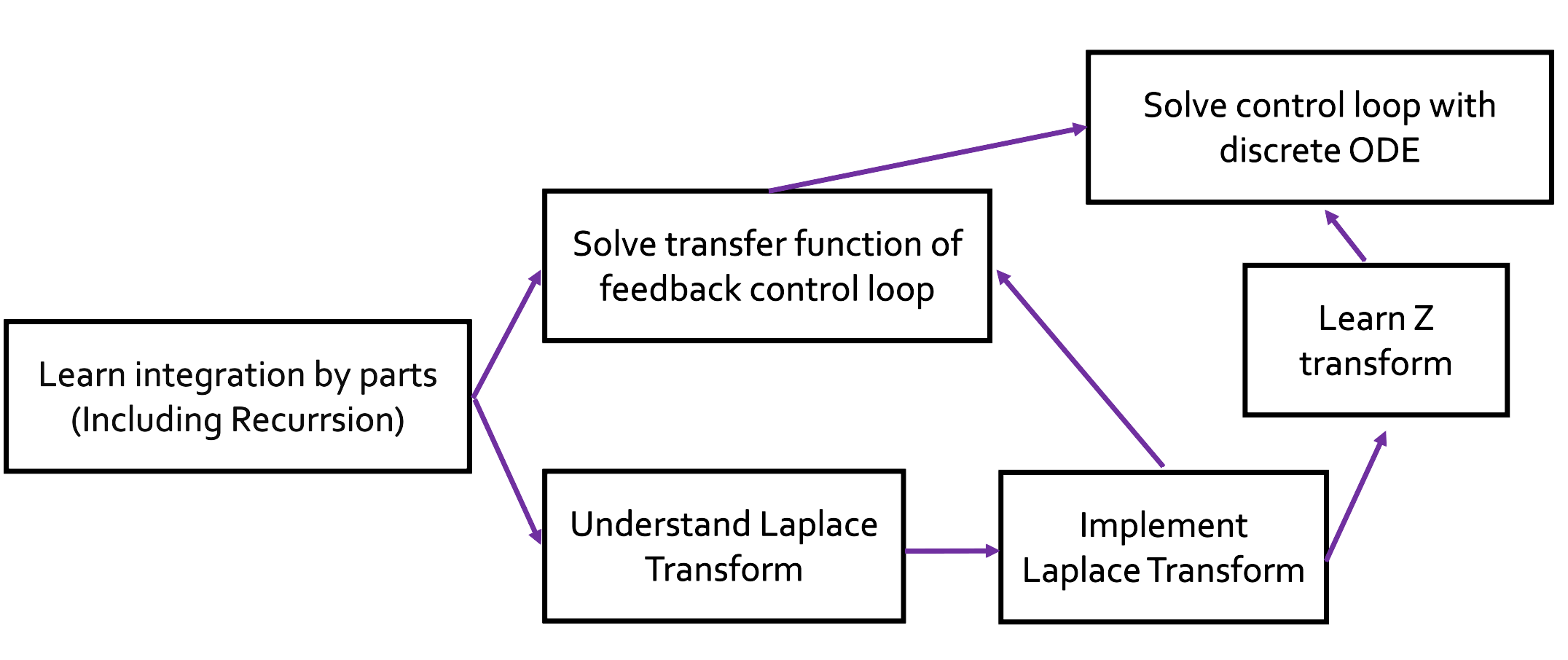
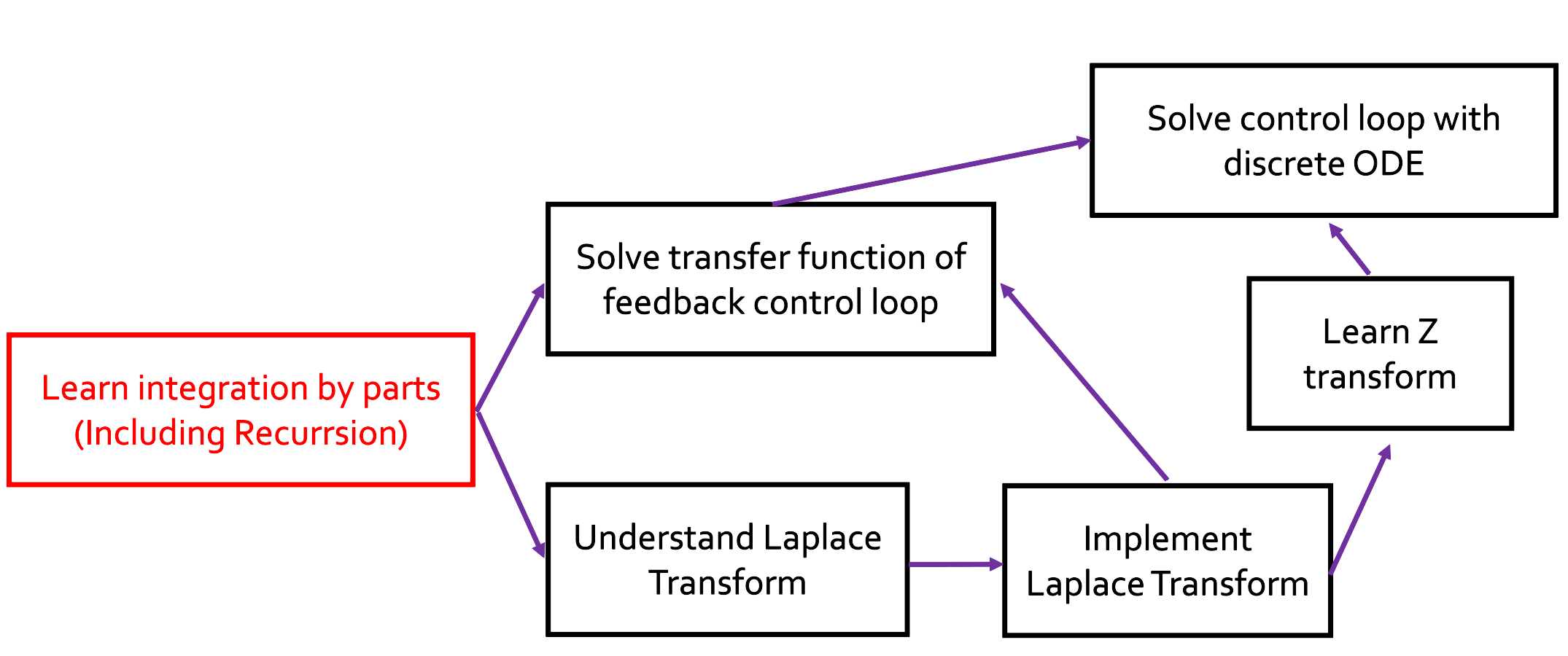
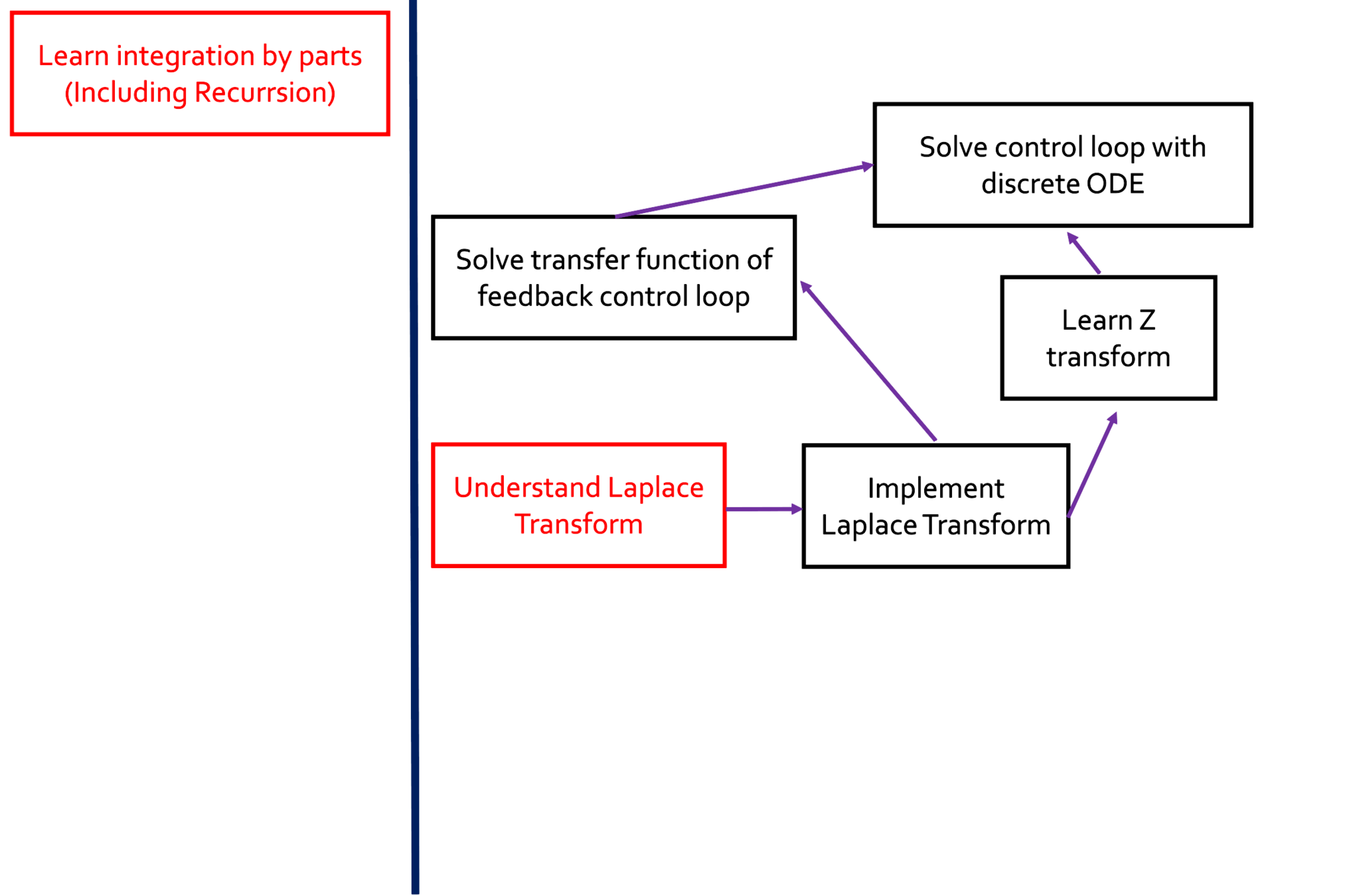
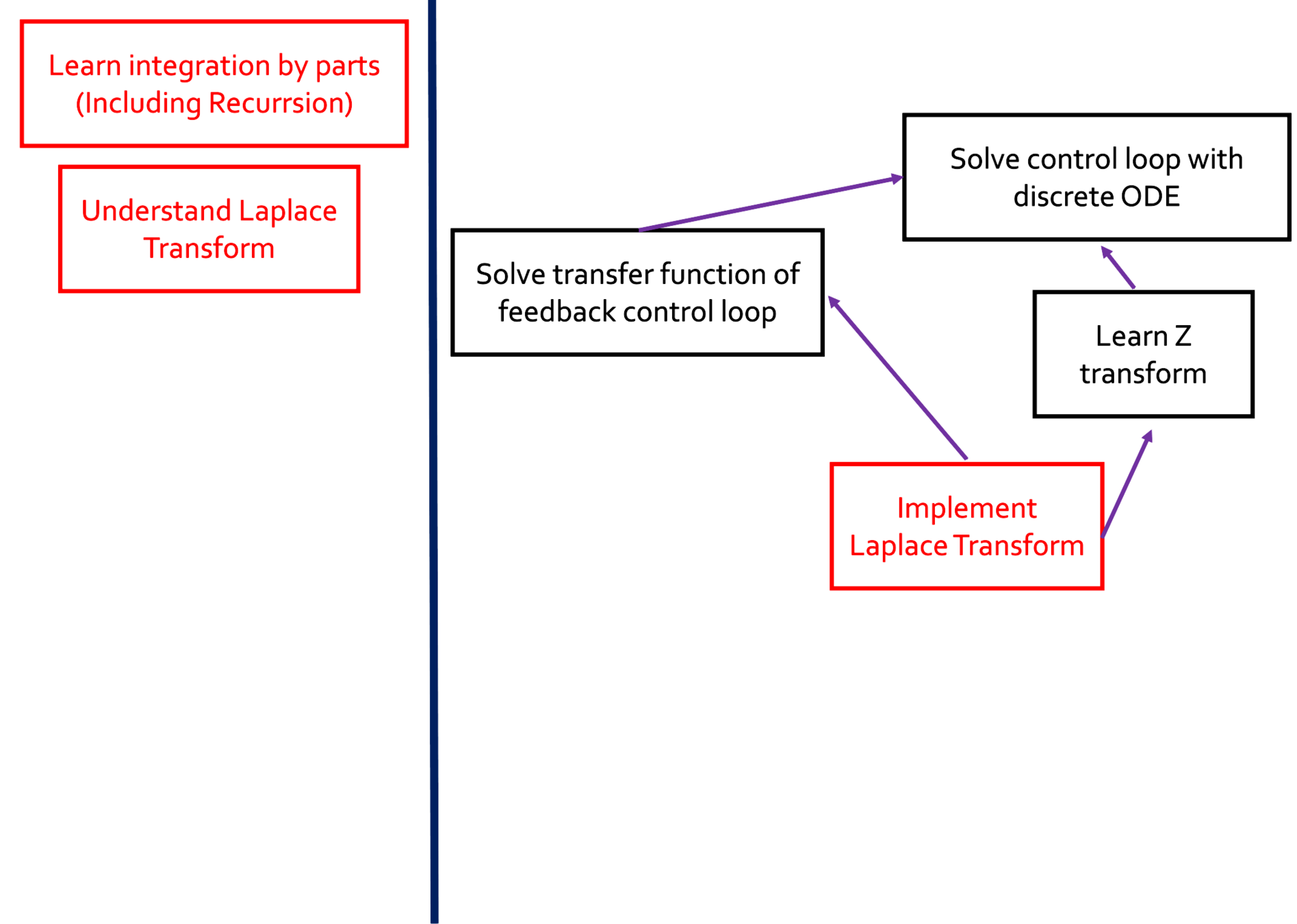
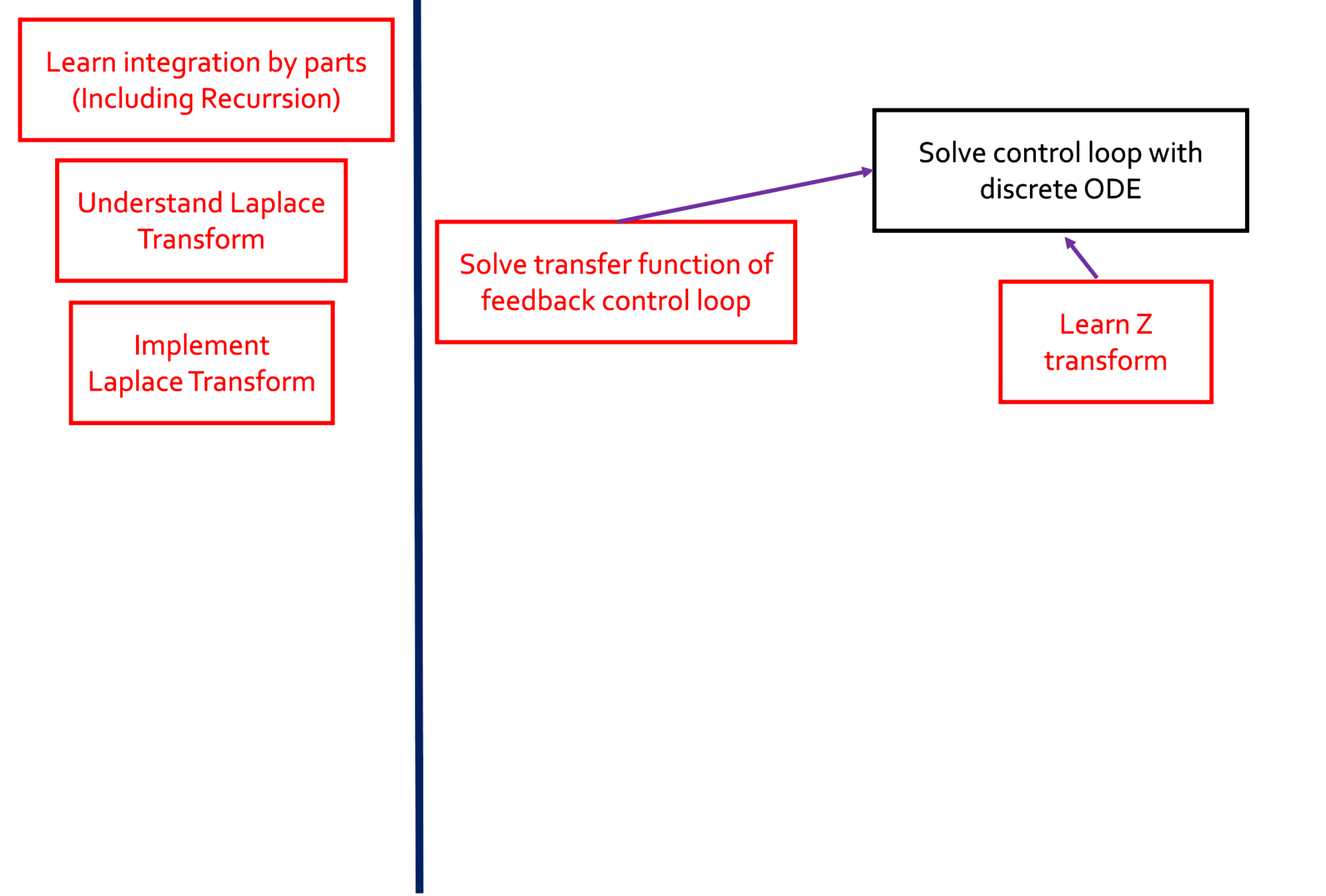


#include<bits/stdc++.h>
using namespace std;
#define mx 200005
vector<int>g[mx];
int visited[mx];
stack<int>s;
void dfs(int u)
{
visited[u]=1;
for(int i=0; i<g[u].size(); i++)
{
int v=g[u][i];
if(visited[v]==0) dfs(v);
}
s.push(u);
}
int main()
{
int n;
cin>>n; //number of vertex
int m;
cin>>m; //number of edges
while(m--)
{
int u,v;
cin>>u>>v;
g[u].push_back(v); //making one directional graph
}
for(int i=1;i<=n;i++){
if(visited[i]==0) dfs(i);
}
for(int i=0; i<n; i++)
{
int x=s.top();
x.pop();
cout<<x<" ";
}
cout<<endl;
}Program evaluation and review technique(PERT)
A project management technique called Pert involves breaking a large project into a number of tasks, estimating the time required to perform each task, and determining which tasks can not be started until others have been completed. The project is then summarized in chart form. For example, the chart
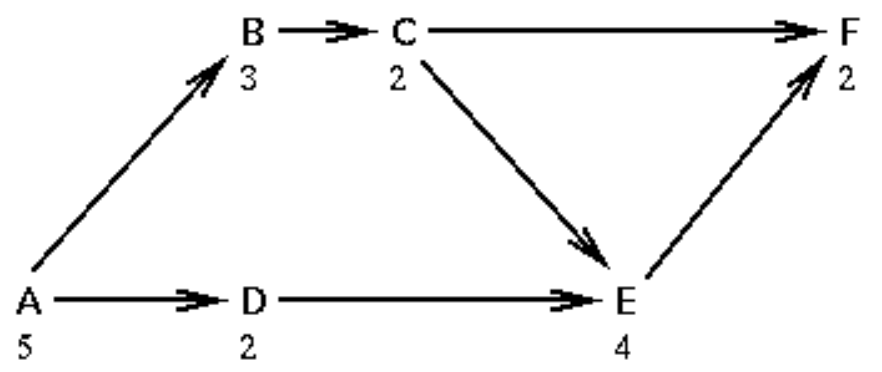
indicates that tasks A, B, C, D, E and F each take 5, 3, 2, 2, 4, and 2 days respectively, that task E cannot complete until C and D are both completed, but that D can be performed in parallel with B and C. Write a program that accepts a Pert chart and computes the amount of time required to complete a project.
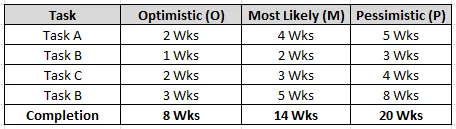
Step 1-4: Formula: (P+4M+O)/6
Example: (8 + 4(14)+20)/6 = 14 Weeks
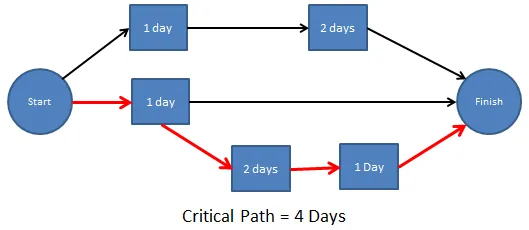
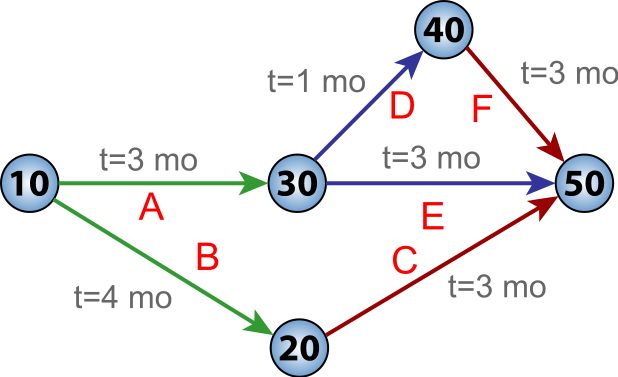
Step 1-1: 活動網路
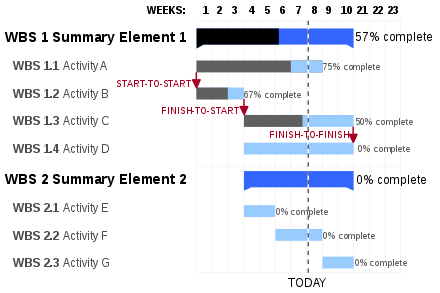
Step 2: 甘特圖
Step3: 關鍵路徑法 via Dynamic Programming
the longest sequence of activities that must be finished on time in order for the entire project to be complete.
Step 1-2: Topological Sort
#include <stdio.h>
#include <string.h>
int main() {
int t, v;
char line[100], h[2];
scanf("%d ", &t);
while(t--) {
int map[26][26] = {}, day[26] = {}, mt[26] = {};
int i, j, done[26] = {};
while(gets(line)) {
if(line[0] == '\0')
break;
sscanf(line, "%s %d", h, &v);
j = h[0]-'A', done[j] = 1;
day[j] = v;
for(i = strlen(line)-1; i >= 0; i--) {
if(line[i] < 'A' || line[i] > 'Z')
break;
map[j][mt[j]++] = line[i]-'A';
}
}
int fin[26] = {}, used[26] = {};
int max, ans = 0;
while(1) {
int flag = 0;
for(i = 0; i < 26; i++) {
if(used[i] == 0 && done[i] == 1) {
max = 0;
for(j = 0; j < mt[i]; j++) {
if(used[map[i][j]] == 0)
break;
if(fin[map[i][j]] > max)
max = fin[map[i][j]];
}
if(j == mt[i]) {
fin[i] = max+day[i];
if(fin[i] > ans)
ans = fin[i];
used[i] = 1;
flag = 1;
}
}
}
if(flag == 0)
break;
}
printf("%d\n", ans);
if(t)
puts("");
}
return 0;
}- https://web.ntnu.edu.tw/~algo/DirectedAcyclicGraph.html
- https://en.wikipedia.org/wiki/Program_evaluation_and_review_technique
- https://en.wikipedia.org/wiki/Gantt_chart
- https://github.com/lsiddiqsunny/Topological-sort/blob/master/toposortbydfs.cpp
- https://www.geeksforgeeks.org/topological-sorting/
- https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=6&page=show_problem&problem=393
- https://github.com/morris821028/UVa/blob/master/volume004/452%20-%20Project%20Scheduling.cpp
- https://acqnotes.com/acqnote/tasks/pert-analysis
Qiskit Tutorial
Reference:
- Qubit by Qubit of The Coding School
- Qiskit
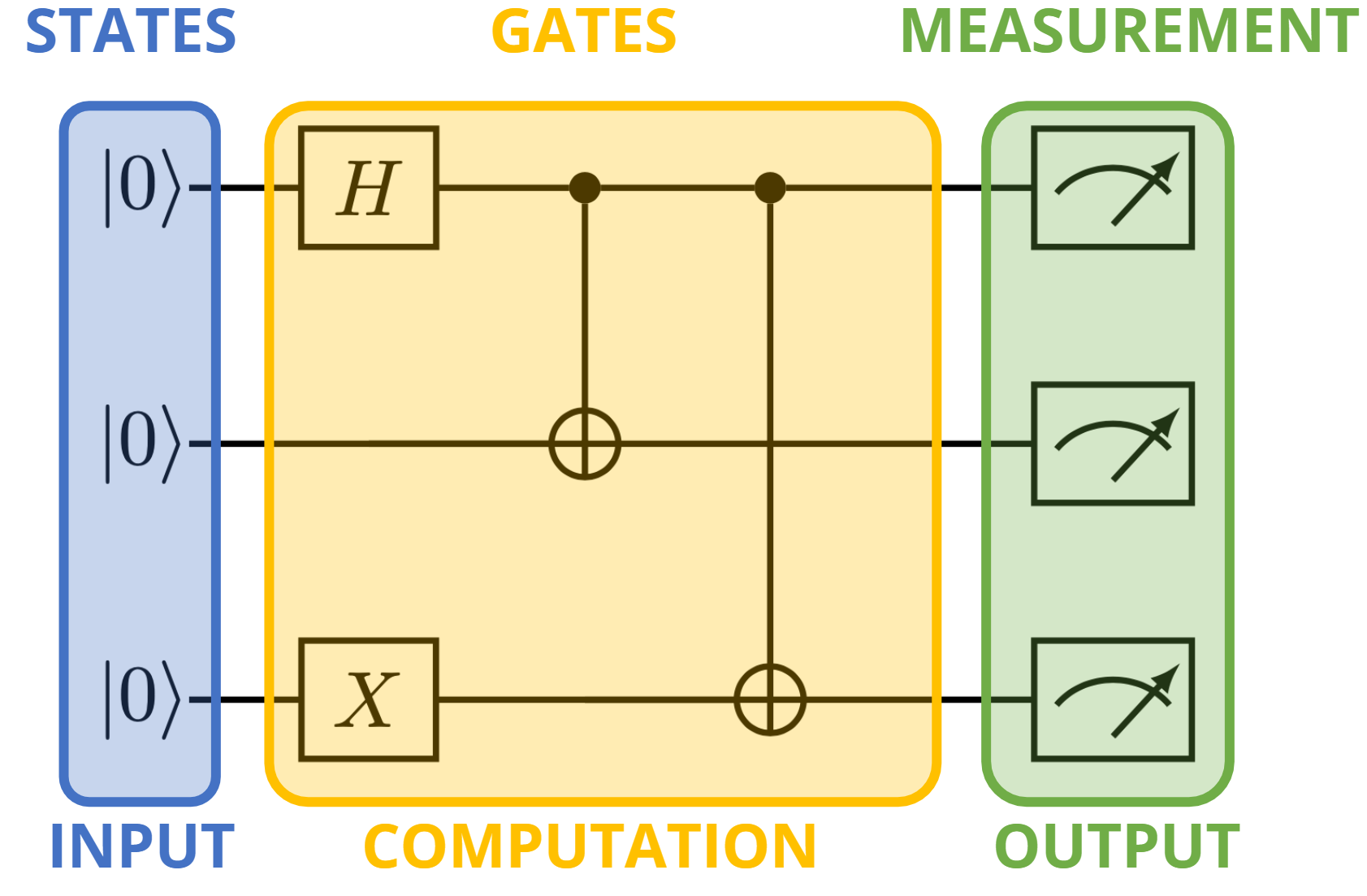

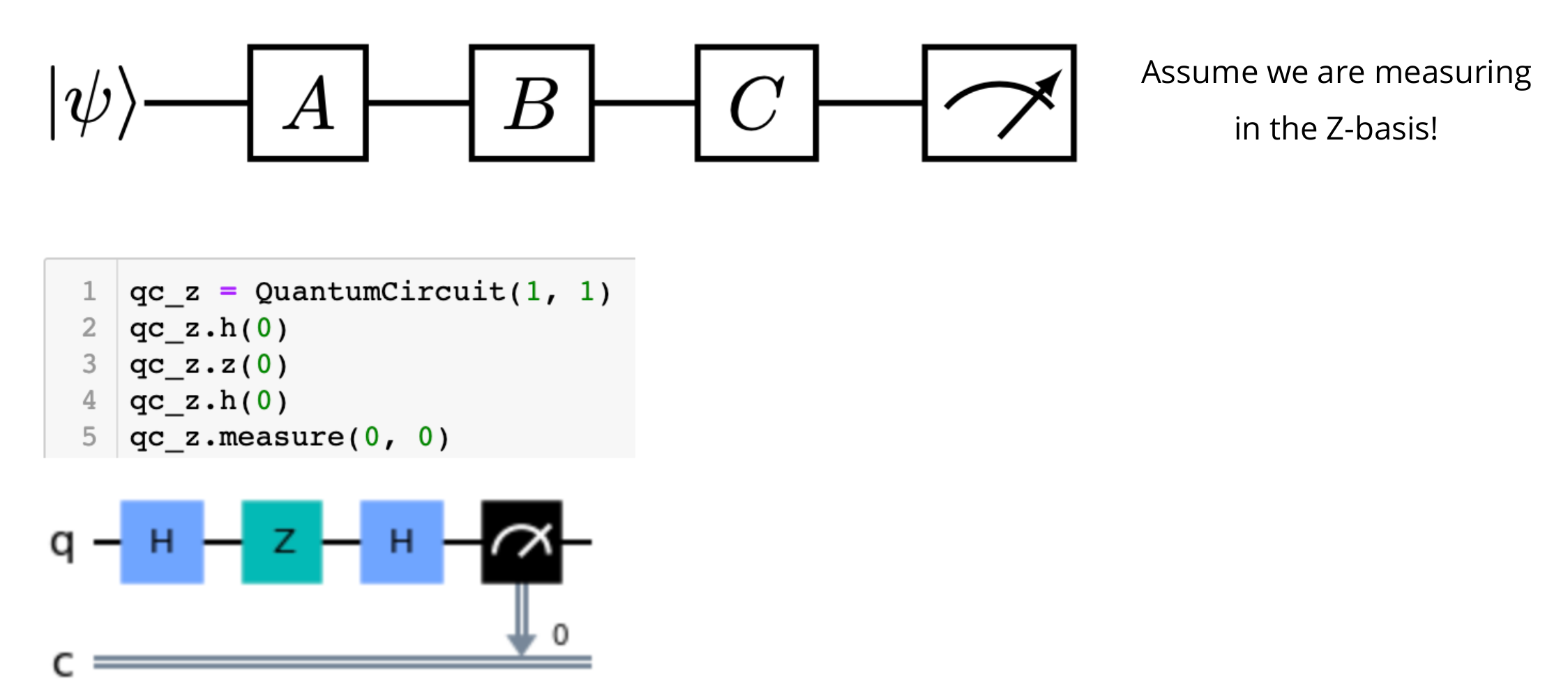
Linear Operation
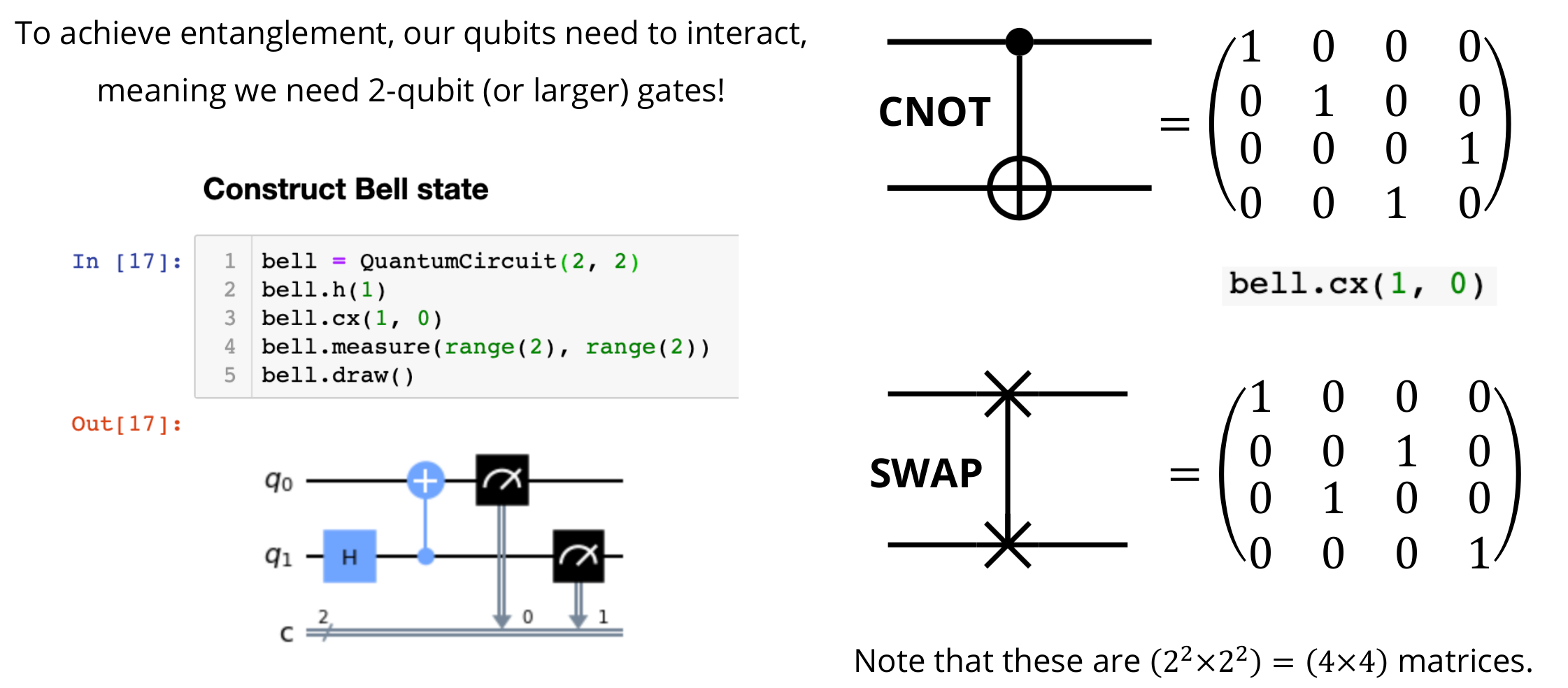
Multi-Qubit gates
Quantum Algorithms
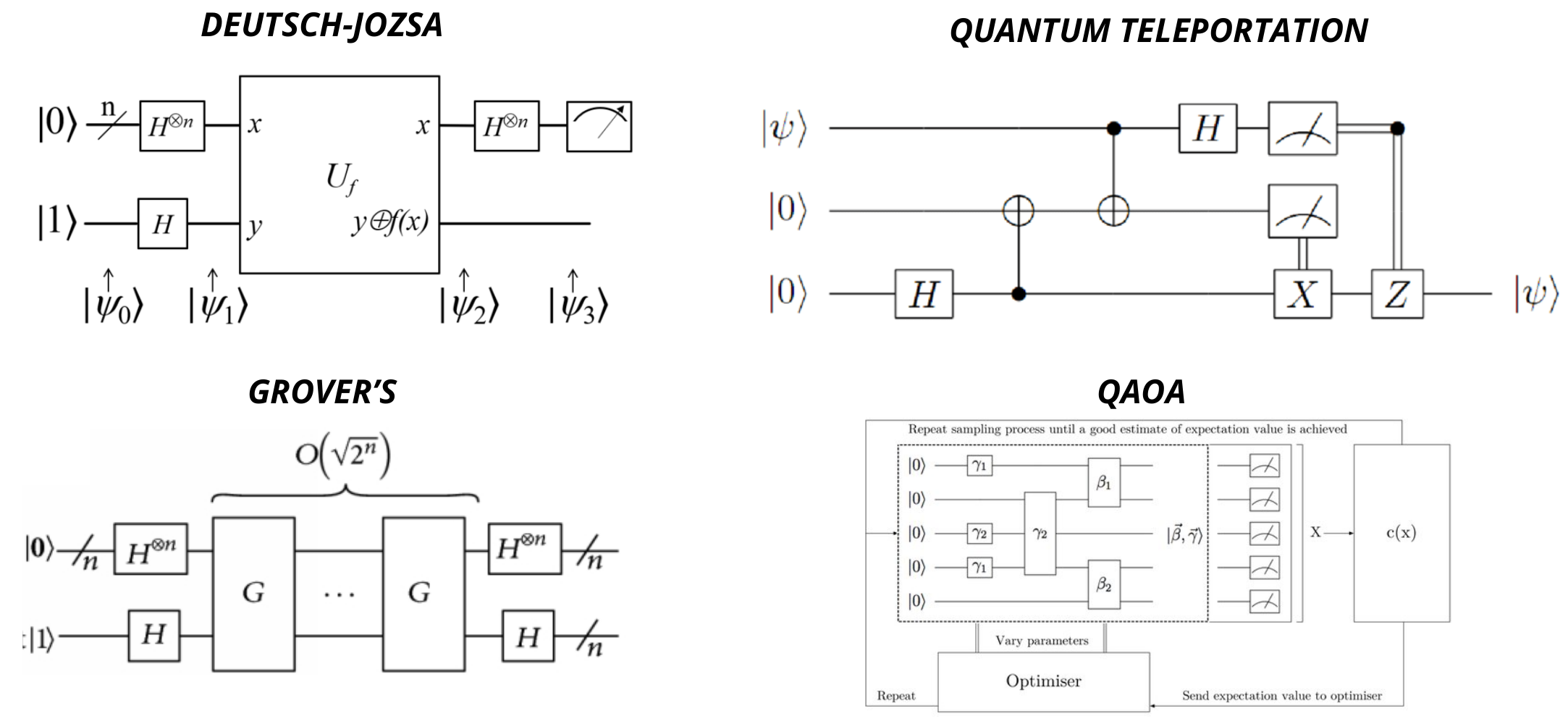
Structure of Qiskit
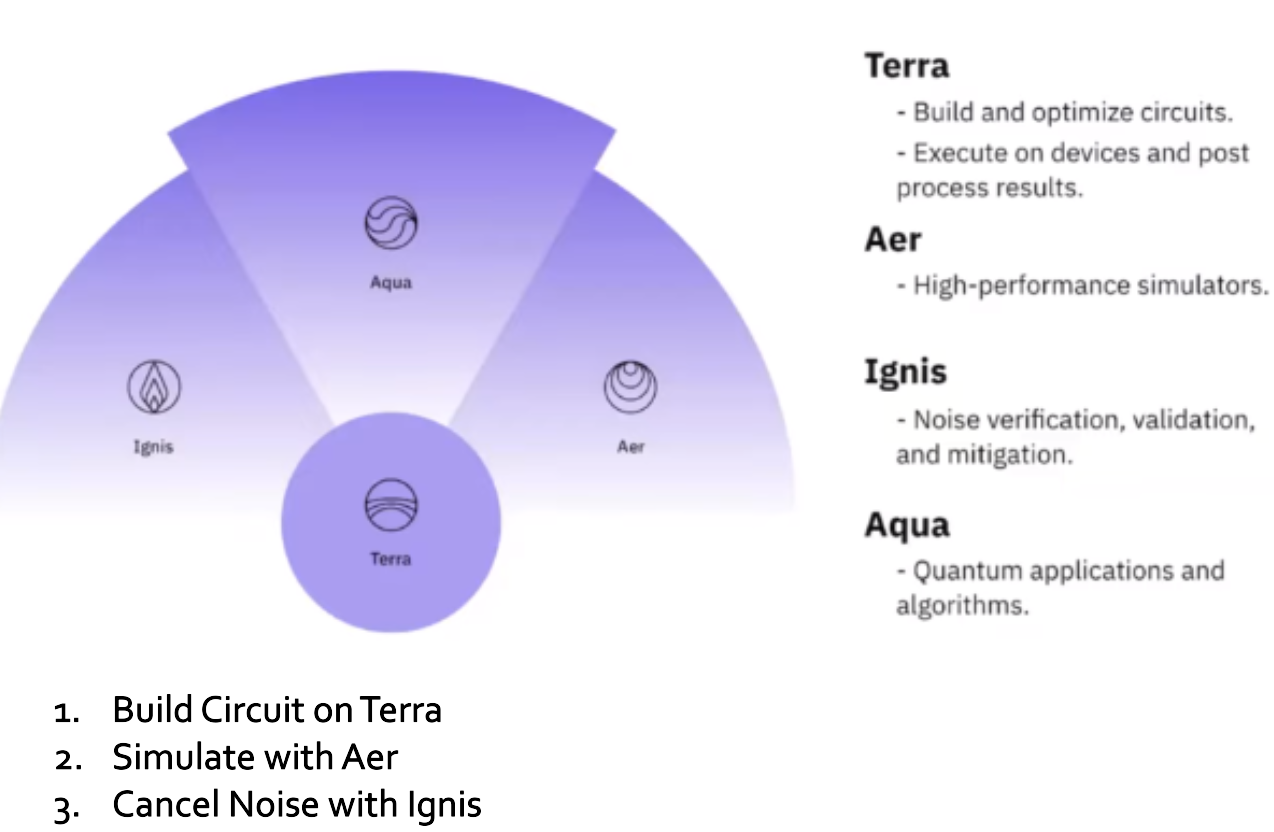
Import
# Basis
import matplotlib.pyplot as plt
import numpy as np
import qiskit as q
from math import pi
from qiskit import *
# Plot data
from qiskit.visualization import plot_histogram
from qiskit.tools.monitor import job_monitor
# Quantum Circuit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
# Simulator
from qiskit import BasicAer
# Tell matplotlib that we are in an Ipython notebook
%matplotlib inlineDesign Circuits
# This creates a quantum circuit object
circ = q.QuantumCircuit(1,1)
# This prints out a diagram of the circuit, the "mpl" makes it look pretty!
display(circ.draw(output="mpl"))
# Linear operation to qubit 0
circ.h(0)
circ.z(0)
circ.h(0)
display(circ.draw(output="mpl"))
# Multi-qubit
circ = q.QuantumCircuit(15,1)
circ.x(6)
display(circ.draw(output="mpl"))
# rz gate
circ.rz(m.pi,0)
display(circ.draw(output="mpl"))
# Call Aer for simulation
backend=q.Aer.get_backend('statevector_simulator')
job = q.execute(circ, backend)
result = job.result()
counts = result.get_counts(circ)
graph = q.visualization.plot_histogram(counts)
display(graph)
# Bell state: Φ+
phi_plus = q.QuantumCircuit(2)
phi_plus.h(0)
phi_plus.cx(0,1)
display(phi_plus.draw(output="mpl"))
# Bell state: Φ- (Use Built-in Function)
circ_phiminus = QuantumCircuit(2,2)
circ_phiminus.h(0)
circ_phiminus.draw('mpl')Design Circuits
# Build Quantum Circuit
circ_phiminus = QuantumCircuit(2,2)
circ_phiminus.h(0)
circ_phiminus.draw('mpl')
circ_phiminus.z(0) #Applying a Z gate to qubit 0
circ_phiminus.cx(0,1) #adding CNOT gate with qubit 0 as control and qubit 1 as target
circ_phiminus.measure([0,1],[0,1]) # Measure output --> Classical bit
circ_phiminus.draw('mpl')
backend = Aer.get_backend('qasm_simulator') # specifying that we will use qasm simulator
job = execute(circ_phiminus, backend, shots = 1024) # shots=1024 specifies that the circuit will be run 1024 times
result = job.result()
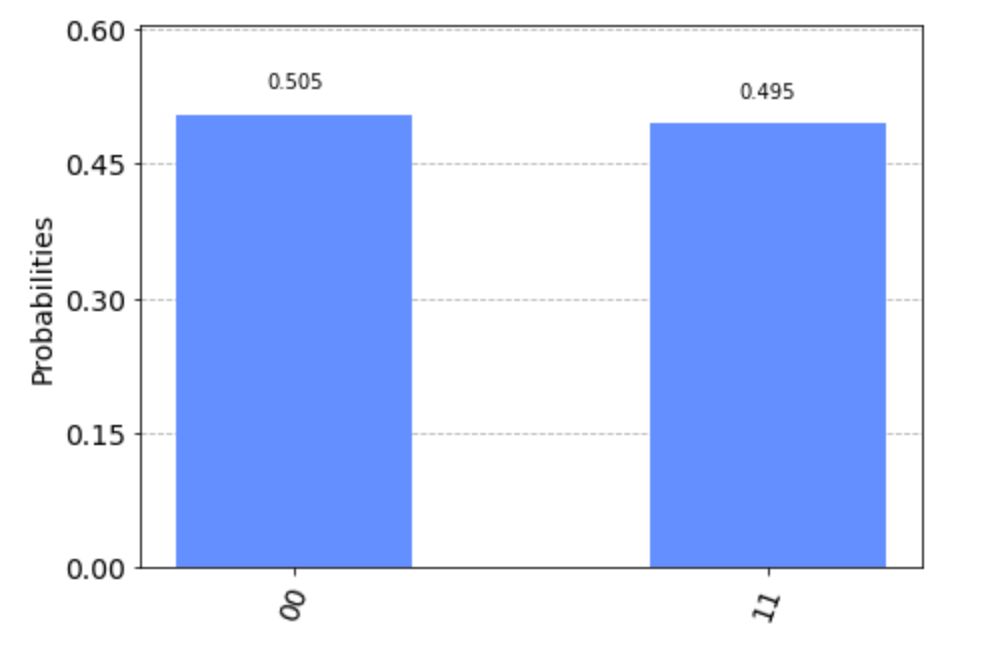
# getting the counts, i.e., the fraction of times the circuit gave all the possible results
counts = result.get_counts(circ_phiminus)
graph = plot_histogram(counts)
display(graph)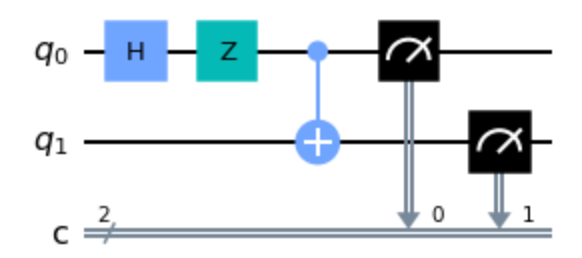
from qiskit_ibm_runtime import QiskitRuntimeService
options = {
'backend_name': 'ibmq_qasm_simulator'
}
runtime_inputs = {
# A PyTorch-compatible loss function. Can be one of the official PyTorch loss
# functions from ``torch.nn.loss or a custom function defined by the user.
'loss_func': None, # [object,object] (required)
# A hybrid QNN model to
# be trained.
'model': None, # object (required)
# A PyTorch optimizer to tune
# the model parameters.
'optimizer': None, # object (required)
# A PyTorch data loader object
# containing the training dataset.
'train_data': None, # object (required)
}
service = QiskitRuntimeService(
channel='ibm_quantum'
)
job = service.run(
program_id='torch-train',
options=options,
inputs=runtime_inputs,
instance='ibm-q/open/main'
)
# Job id
print(job.job_id)
# See job status
print(job.status())
# Get results
result = job.result()QNN
Runtime Program
A program that is made in order to facilitate (make easier) develop process
Applied Programming and Algorithms
By 洪宇辰
Applied Programming and Algorithms
- 20

