Regularized Composite ReLU-ReHU Loss Minimization with Linear Computation and Linear Convergence



Ben Dai (CUHK)
(Joint work with Yixuan Qiu)
SVM
-
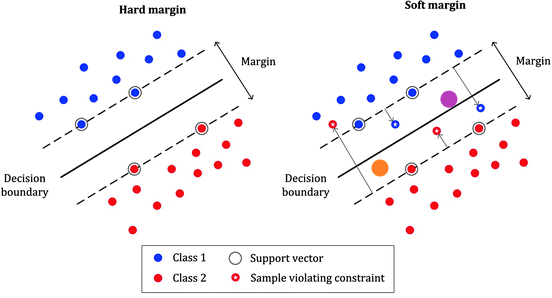
Support Vector Machines (SVMs) were introduced by Vapnik and Chervonenkis in the 1990s, building on VC theory 1960s.
-
SVM and Kernel SVM gained widespread popularity in the late 1990s and early 2000s, and impressive empirical performance across various applications.
-
LIBSVM, developed by Lin in 2000, became the most widely-used SVM software.
- downloaded millions of times
- Cited by 50K +
Source: https://stackoverflow.com/questions/73589036/clarity-needed-on-svm-concepts
LIBLINEAR
- LIBLINEAR is the winner of ICML 2008 large-scale learning challenge (linear SVM track). It is also used for winning KDD Cup 2010.

- In scikit-learn, liblinear is the default solver for SVMs in Python.


LIBLINEAR
As indicated from the official Liblinear website, thanks to contributions from researchers and developers worldwide, Liblinear has incorporated interfaces for various languages:
{ R, Python, Matlab, Java, Perl, Ruby, and even PHP }
The popularity of Liblinear is thus evident.

LIBLINEAR


LIBLINEAR



LIBLINEAR


-
From 2008 to 2025, a 17-year period of continuous contributions.
-
Countless hours have been devoted.
-
Since its development in 2008, it has consistently remained the No. 1 solver for solving SVMs.

Dual Coordinate Desent
The primal is QP with 2n linear constraints
Given a training set of \(n\) points of the form \((\mathbf{x}_i, y_i)_{i=1}^n\), where \(y = \pm 1\) which indicates the binary label of the \(i\)-th instance \( \mathbf{x}_i \in \mathbb{R}^d \).
Primal form.
$$ \min_{\pmb{\beta}, \xi} \sum_{i=1}^{n} C_i \xi_i + \frac{1}{2} \| \pmb{\beta} \|^2 $$
$$y_i \pmb{\beta}^T \mathbf{x}_i \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad i = 1, \ldots, n$$
$$\min_{\pmb{\beta}} \sum_{i=1}^{n} C_i ( 1 - y_i \pmb{\beta}^T \mathbf{x}_i )_+ + \frac{1}{2} \| \pmb{\beta} \|^2 $$
After introducing some slack variables,
Dual Coordinate Desent
The dual is a box-constrained QP
- simpler form than the primal problem
- naturally leads to coordinate descent (CD)
- Lagrange multiplier
$$L_P = \sum_{i=1}^{n} C_i \xi_i + \frac{1}{2} \| \pmb{\beta} \|^2 - \sum_{i=1}^n \alpha_i \big( y_i \mathbf{x}_i^T \pmb{\beta} - (1 - \xi_i) \big) - \sum_{i=1}^n \mu_i \xi_i$$
- Taking derivatives to w.r.t. \( \pmb{\beta} \) and \( \xi_i \):
$$ \pmb{\beta} = \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i, \quad \alpha_i = C_i - \mu_i, $$
Dual form:
$$ \min_{\pmb{\alpha}} \frac{1}{2} \pmb{\alpha}^T \mathbf{Q} \pmb{\alpha} - \mathbf{1}^T \pmb{\alpha}, \quad \text{s.t.} \quad 0 \leq \alpha_i \leq C_i$$
KKT Condition
Dual Coordinate Desent
- Lagrange multiplier
$$L_P = \sum_{i=1}^{n} C_i \xi_i + \frac{1}{2} \| \pmb{\beta} \|^2 - \sum_{i=1}^n \alpha_i \big( y_i \mathbf{x}_i^T \pmb{\beta} - (1 - \xi_i) \big) - \sum_{i=1}^n \mu_i \xi_i$$
- Taking derivatives to w.r.t. \( \pmb{\beta} \) and \( \xi_i \):
$$ \pmb{\beta} = \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i, \quad \alpha_i = C_i - \mu_i, $$
Dual form:
$$ \min_{\pmb{\alpha}} \frac{1}{2} \pmb{\alpha}^T \mathbf{Q} \pmb{\alpha} - \mathbf{1}^T \pmb{\alpha}, \quad \text{s.t.} \quad 0 \leq \alpha_i \leq C_i$$
KKT Condition

The dual is a box-constrained QP
- simpler form than the primal problem
- naturally leads to coordinate descent (CD)
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
Note that \( (\mathbf{Q} \mathbf{\alpha})_{i} = y_i \mathbf{x}_i^T \sum_{j=1}^n y_j \mathbf{x}_j \alpha_j \)
\( O(nd) \)
(at least O(n) if Q is pre-computed)
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
Note that \( (\mathbf{Q} \mathbf{\alpha})_{i} = y_i \mathbf{x}_i^T \sum_{j=1}^n y_j \mathbf{x}_j \alpha_j \)
\( O(nd) \)
(at least O(n) if Q is pre-computed)
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
\( O(n^2) \)
Loop over \((i=1,\cdots,n)\)
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
\( O(n^2) \)
Loop over \((i=1,\cdots,n)\)
- IPM
- ADMM
- ...
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
Note that \( (\mathbf{Q} \mathbf{\alpha})_{i} = y_i \mathbf{x}_i^T \sum_{j=1}^n y_j \mathbf{x}_j \alpha_j \)
\( O(nd) \)
KKT Condition
$$ \pmb{\beta} = \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i $$
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
Note that \( (\mathbf{Q} \mathbf{\alpha})_{i} = y_i \mathbf{x}_i^T \sum_{j=1}^n y_j \mathbf{x}_j \alpha_j \)
\( O(nd) \)
$$= y_i \mathbf{x}^T_i \mathbf{\beta}$$
KKT Condition
$$ \pmb{\beta} = \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i $$
\( O(d) \)
Dual Coordinate Desent
$$ \min_{\delta_i} \frac{1}{2} Q_{ii} \delta_i^2 + \big((\mathbf{Q} \pmb{\alpha})_i - 1\big) \delta_i, \quad \text{s.t.} \quad -\alpha_i \leq \delta_i \leq C_i - \alpha_i$$
where \( \mathbf{Q}_{ij} = y_i y_j \mathbf{x}^T_i \mathbf{x}_j \). The solution to the sub-problem is:
CD sub-problem. Given an "old" value of \( \pmb{\alpha} \), we solve
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - ( (\mathbf{Q}\pmb{\alpha})_i )}{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i$$
\( O(n^2) \)
Loop over \((i=1,\cdots,n)\)
$$ \delta^*_i = \max \Big( -\alpha_i, \min\big( C_i - \alpha_i, \frac{1 - y_i \pmb{\beta}^T\mathbf{x}_i }{Q_{ii}} \big) \Big) $$
$$ \alpha_i^* \leftarrow \alpha_i + \delta^*_i, \quad \pmb{\beta} \leftarrow \pmb{\beta} + \delta^* y_i \mathbf{x}_i$$
\( O(nd) \)
Loop over \((i=1,\cdots,n)\)
pure CD
primal-dual CD
LIBLINEAR
-
What contributes to the rapid efficiency of Liblinear?
- Analytic solution of each CD updates
- Reduce \( O(n^2) \) to \(O(nd)\) in CD updates
- Linear convergence \( O(\log(\epsilon^{-1})) \)
- CD usually is sublinear convergence
- Linear structure improves the convergence!

Source: Ryan Tibshirani, Convex Optimization, lecture notes
LIBLINEAR
-
What contributes to the rapid efficiency of Liblinear?
- Analytic solution of each CD updates
- Reduce \( O(n^2) \) to \(O(nd)\) in CD updates
- Linear convergence \( O(\log(\epsilon^{-1})) \)
- CD usually is sublinear convergence
- Linear structure improves the convergence!
Luo, Z. Q., & Tseng, P. (1992). On the convergence of the coordinate descent method for convex differentiable minimization. Journal of Optimization Theory and Applications.



LIBLINEAR
-
What contributes to the rapid efficiency of Liblinear?
- Analytic solution of each CD updates
- Reduce \( O(n^2) \) to \(O(nd)\) in CD updates
- Linear convergence \( O(\log(\epsilon^{-1})) \)
- CD usually is sublinear convergence
Combine Linear KKT in CD updates.
Extension. When the idea of "LibLinear" can be applied?
$$L_P = \sum_{i=1}^{n} C_i \xi_i + \frac{1}{2} \| \pmb{\beta} \|^2 - \sum_{i=1}^n \alpha_i \big( y_i \mathbf{x}_i^T \pmb{\beta} - (1 - \xi_i) \big) - \sum_{i=1}^n \mu_i \xi_i$$
ReHLine
Extension. When the idea of "LibLinear" can be applied?
-
Loss
- hinge loss in SVMs (✔)
- check loss in Quantile Reg (✔)
- More?
- Many piecewise linear / quad (✔)
- A class of losses? PLQ (✔)
Linear KKT Conditions

ReHLine
Extension. When the idea of "LibLinear" can be applied?
-
Loss
- hinge loss in SVMs (✔)
- check loss in Quantile Reg (✔)
- order > 2 (✘)
- A class of losses? PLQ (✔)

-
Constraints
- box constraints? (✔)
- linear constraints (✔)
Linear KKT Conditions
ReHLine
In this paper, we consider a general regularized ERM based on a convex PLQ loss with linear constraints:
\( \min_{\mathbf{\beta} \in \mathbb{R}^d} \sum_{i=1}^n L_i(\mathbf{x}_i^\intercal \mathbf{\beta}) + \frac{1}{2} \| \mathbf{\beta} \|_2^2, \quad \text{ s.t. } \mathbf{A} \mathbf{\beta} + \mathbf{b} \geq \mathbf{0}, \)
-
\( L_i(\cdot) \geq 0\) is the proposed composite ReLU-ReHU loss.
-
\( \mathbf{x}_i \in \mathbb{R}^d\) is the feature vector for the \(i\)-th observation.
-
\(\mathbf{A} \in \mathbb{R}^{K \times d}\) and \(\mathbf{b} \in \mathbb{R}^K\) are linear inequality constraints for \(\mathbf{\beta}\).
-
We focus on working with a large-scale dataset, where the dimension of the coefficient vector and the total number of constraints are comparatively much smaller than the
sample sizes, that is, \(d \ll n\) and \(K \ll n\).
ReHLine Loss
Definition 1 (Dai and Qiu. 2023). A function \(L(z)\) is composite ReLU-ReHU, if there exist \( \mathbf{u}, \mathbf{v} \in \mathbb{R}^{L}\) and \(\mathbf{\tau}, \mathbf{s}, \mathbf{t} \in \mathbb{R}^{H}\) such that
\( L(z) = \sum_{l=1}^L \text{ReLU}( u_l z + v_l) + \sum_{h=1}^H \text{ReHU}_{\tau_h}( s_h z + t_h)\)
where \( \text{ReLU}(z) = \max\{z,0\}\), and \( \text{ReHU}_{\tau_h}(z)\) is defined below.


Theorem 1 (Dai and Qiu. 2023). A loss function \(L:\mathbb{R}\rightarrow\mathbb{R}_{\geq 0}\) is convex PLQ if and only if it is composite ReLU-ReHU.
ReHLine Formulation

\( \min_{\mathbf{\beta} \in \mathbb{R}^d} \sum_{i=1}^n L_i(\mathbf{x}_i^\intercal \mathbf{\beta}) + \frac{1}{2} \| \mathbf{\beta} \|_2^2, \quad \text{ s.t. } \mathbf{A} \mathbf{\beta} + \mathbf{b} \geq \mathbf{0}, \)

can also handle elastic-net penalty.
ReHLine Results
A broad range of problems. ReHLine applies to any convex piecewise linear-quadratic loss function (potential for non-smoothness included) with any linear constraints, including the hinge loss, the check loss, the Huber loss, etc.

Super efficient. ReHLine has a linear convergence rate. The per-iteration computational complexity is linear in the sample size.
ReHLine Algo
- Inspired by CD and Liblinear

The linear relationship between primal and dual variables greatly simplifies the computation of CD.
ReHLine Algo

ReHLine Algo


ReHLine Algo





Software. generic/ specialized software
- cvx/cvxpy
- mosek (IPM)
- ecos (IPM)
- scs (ADMM)
- dccp (DCP)
- liblinear -> SVM
- hqreg -> Huber
- lightning -> sSVM
Experiments
- 1000x speed-up for generic solvers
- no worse than specialized solvers
ReHLine SVM



LIBLINEAR
ReHLine
ReHLine QR
We illustrate our algo in QR using the simulated example from Generate the “Friedman #1” regression problem:

ReHLine QR
We illustrate our algo in QR using the simulated example from Generate the “Friedman #1” regression problem:

1M-Scale Quantile Reg
in 0.5 Second with ReHLine
ReHLine Usage
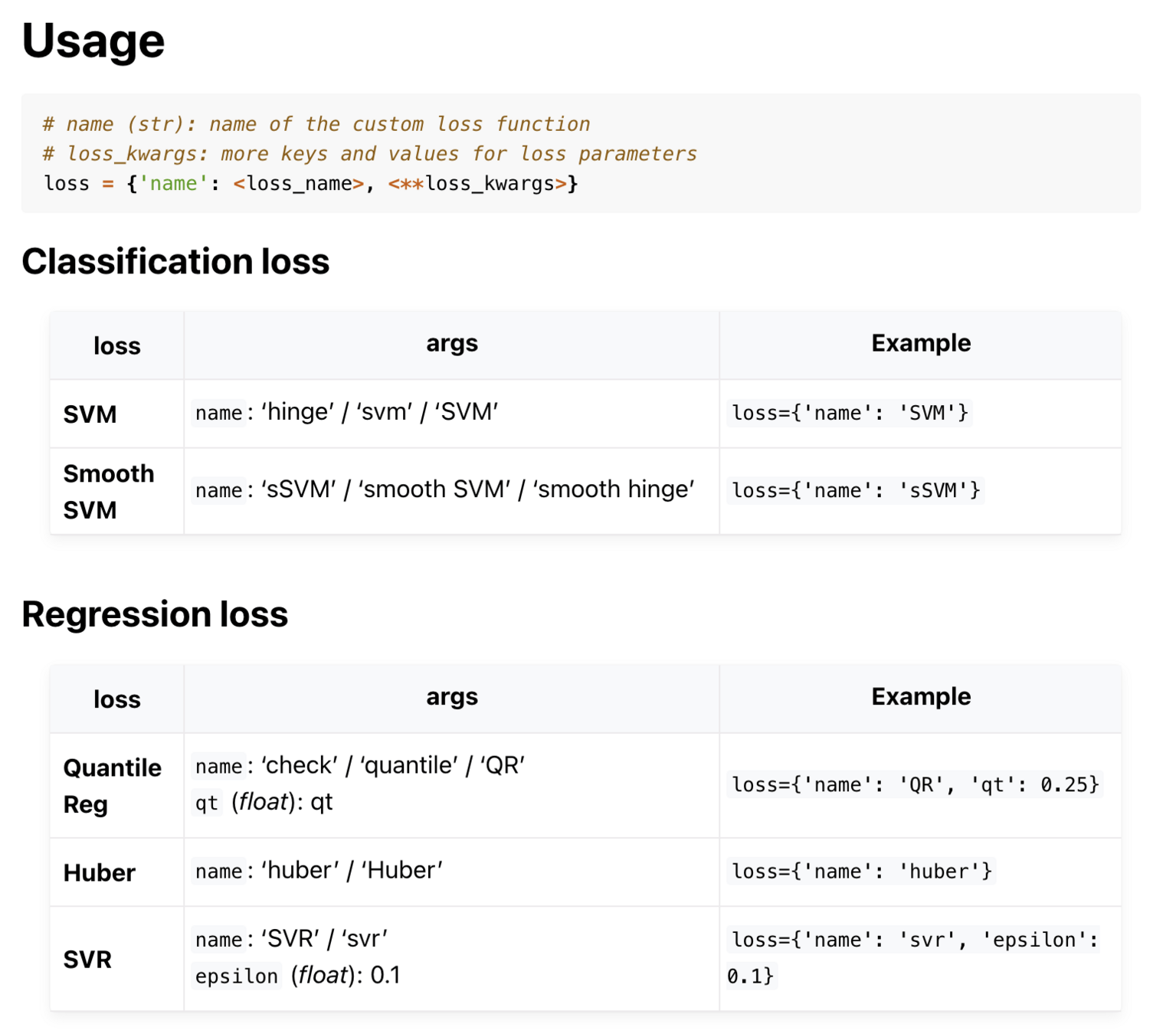
ReHLine Usage


ReHLine Path Solution

ReHLine integrates with the scikit-learn ecosystem
Source:
- https://medium.com/@sahin.samia/scikit-learn-pipelines-explained-streamline-and-optimize-your-machine-learning-processes-f17b1beb86a4
- https://www.analyticsvidhya.com/blog/2021/06/tune-hyperparameters-with-gridsearchcv/
- https://www.mygreatlearning.com/blog/scikit-machine-learning/

plq_Ridge_Classifier
plq_Ridge_Regressor

Over the past year, we have released 7 versions and achieved 51K downloads.
We have completed the following new features in the new version 0.1.1:
1. sklearn estimator compatibility interface that enables seamless integration with existing sklearn pipelines, GridSearchCV, and cross-validation functionality.
2. Fast algorithms for PLQ loss in SVD models and matrix factorization.


-
Powerful Algo
- We have improved the computing power of a large category of Regularized Empirical Risk Minimization to the level of LibLinear (linear convergence + linear computation)
-
Powerful software
- Efficient software and C++ implementation. ReHLine is equivalent to LIBLINEAR within SVM, but our present implementation can be even faster than LIBLINEAR.
- It provides for flexible application concerning losses and constraints through Python/R API, which are intended to tackle a vast array of ML and STAT problems. (e.g. FairSVM).
Summary
Thank you!
If you like ReHLine please star 🌟 our Github repository, thank you!







rehline_full
By statmlben
rehline_full
[NeurIPS2023] Regularized Composite ReLU-ReHU Loss Minimization with Linear Computation and Linear Convergence
- 526



