Making Rational Protein Design “Intelligent”
Richard Chen, Jimmy Kim, Jason Wong, Stewart Slocum
What is Computational Protein Design?
CPD seeks to predict an amino acid sequence for a protein that folds to a given structure.
It's an NP-hard problem.
Protein Design Holds Promise
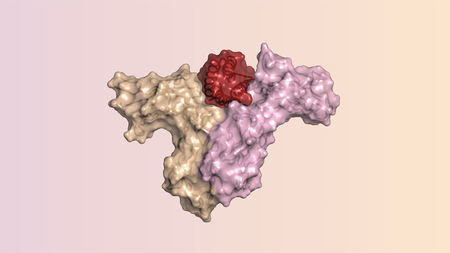
Challenge
Number of possible amino acids grow exponentially as chain size increases. Designing a protein of 100 residues has a solution space of \( 100^{20} \) amino acids before considering side chain flexibility.
Ways of Computing Sequences
- We want to find a sequence that will fold to a given structure, so we optimize the following equation:
- Discrete problem as for each amino acid spot there are only a limited number of possible rotamers and 20 possibilities
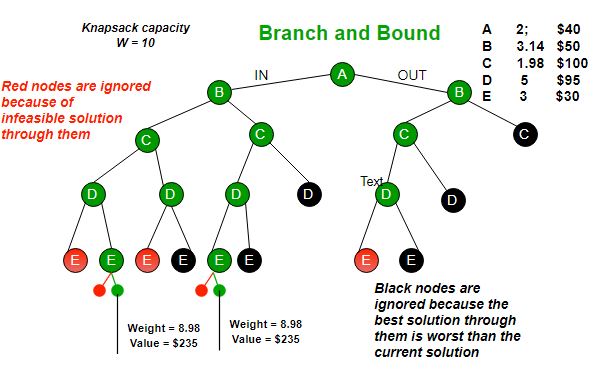
- Current strategies use dead-end elimination then branch and bound
X_i=\{r_i^1, ..., r_i^k\}
\text{min} E_T = \sum_i E_i(r_i) + \sum_{i \neq j} E_{i j}(r_i, r_j)
What We are Doing
Using a DNN to learn to approximate size of subtrees for a given branching variable and value. We will use these scores to pick the best variable-value to branch on, speeding up computation in Toulbar2 an exact solver for Weighted Constraint Satisfaction Problems which has been used in CPD.
Features
Trained by taking static, dynamic, and dynamic optimization features at the current execution of the program.
Some examples (of many):
- Average unary cost of domain values in current variable
- Domain size of variable
- Number of variables with assigned values
- Weighted degree of current variable (how many times it has been involved in a conflict or infeasible solution)
Data Set
35 protein design problems of different orders of difficulty provide a set of consistent (hopefully learnable) instances to train to estimate subtree sizes on.
These problems generate search trees from a size of ~10 nodes to ~10,000. We probabilistically select nodes to include in the data set so that we choose an equal amount of nodes from each level of the tree and bias the data set towards large problems.
DLDO Presentation
By Stewy Slocum
