Seminar 4:
Improving DQN
Artyom Sorokin | 26 Feb
Double DQN
Multi-Steps Returns
Recall Q-learning/DQN target:
y_t =r_t + \gamma \max_{a} Q_{\theta'}(s_{t+1}, a)
The only values that matter if \(Q_{\theta'}\) is bad!
These are important if \(Q_{\theta'}\) is good!
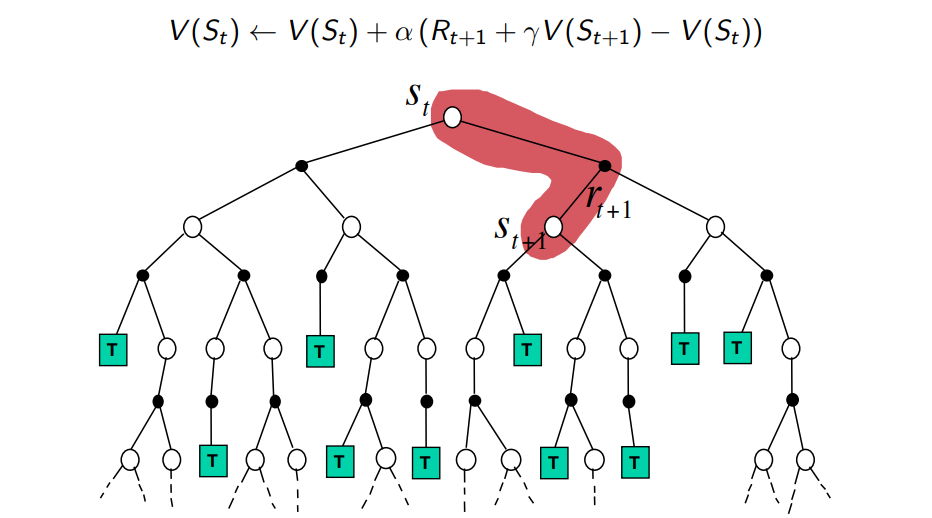
useless estimation at the beggining
noisy but true
Multi-Steps Returns
\textcolor{red}{n=1}\,\,\,\,\,\,\,\, G^{(1)}_t = R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})
\textcolor{red}{n=2}\,\,\,\,\,\,\,\, G^{(2)}_t = R_{t+1} + \gamma R_{t+2} + \gamma^{2} Q(S_{t+2}, A_{t+2})
\textcolor{red}{n=\infty}\,\,\,\,\, G^{(\infty)}_t = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-t-1} R_{T}
Recall N-step Returns:
.
.
.
.
.
.
SARSA/TD-target: High Bias, Low Varaince
MC-target: High Variance, No Bias
SARSA/TD-target: High Bias, Low Varaince
SARSA/TD-target: High Bias, Low Varaince
We can constract similar multi-step targets for Q-learning:
y^{N}_t = \sum^{t+N-1}_{k=t} \gamma^{k-t} r_k + \gamma^{N} \max_{a} Q_{\theta'}(s_{t+N}, a)
Multi-Steps Returns
This multi-step Q-learning target:
y^{N}_t = \sum^{t+N-1}_{k=t} \gamma^{k-t} r_k + \gamma^{N} \max_{a} Q_{\theta'}(s_{t+N}, a)
- Q-learning tries to learn greedy policy: \(\pi(s_t) = argmax_a Q_{\theta}(s_t, a)\)
- Buy these N-steps were sampled with \(e\)-greedy policy!
Multi-Steps Returns
"Multi-step Q-learning target":
y^{N}_t = \sum^{t+N-1}_{k=t} \gamma^{k-t} r_k + \gamma^{N} \max_{a} Q_{\theta'}(s_{t+N}, a)
How to fix:
- just ignore the problem:) Often works very well!
- cut N-steps returns dynamically
For more details: Safe and efficient off-policy reinforcement learning
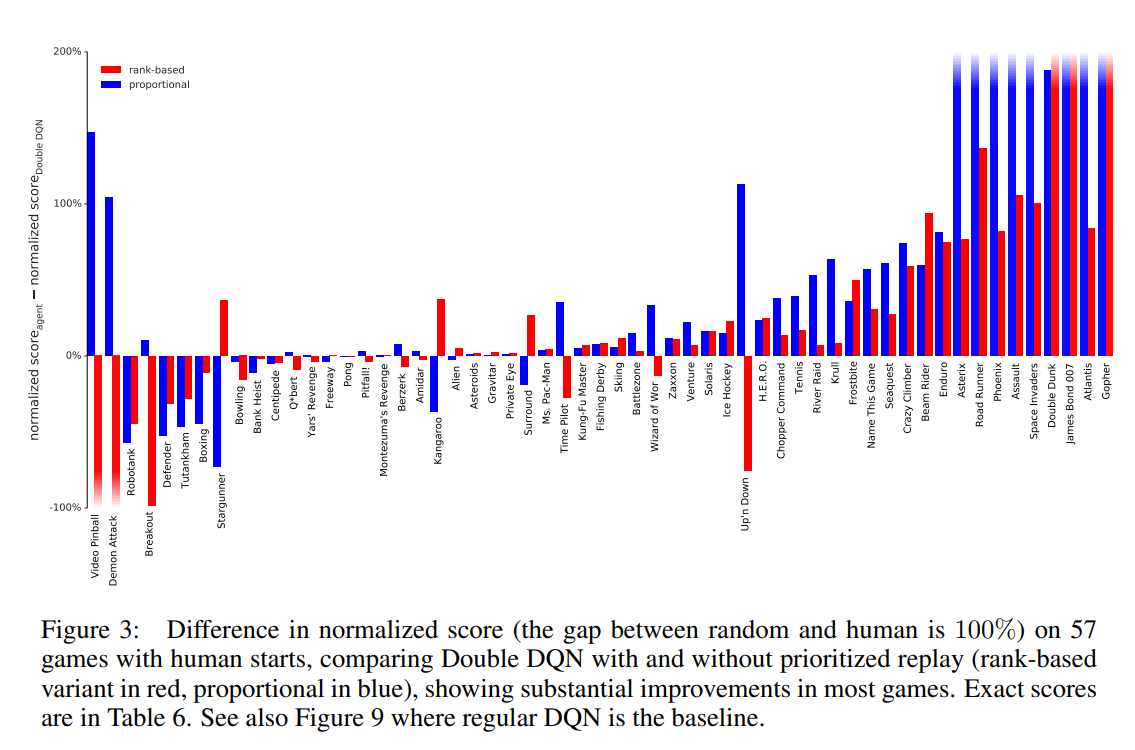
Prioritized Experience Replay
Not all transitions are equally valuable!
Goal: Reach the green target!
Reward: +1 when reaching the target, 0 otherwise
All model estimates all are close to zero: Q(s,a) ~ 0.
Prioritized Experience Replay
Lets prioritize transitions with TD-Error!
\delta_t = r_t + \gamma Q_{\textcolor{blue}{\theta'}}(s_t, argmax_a Q_{\textcolor{red}{\theta}}(s_{t+1}, a)) - Q_{\textcolor{red}{\theta}}(s_t, a_t)
Double DQN TD-Error:
proportional prioritization:
p_i = |\delta_i| + \epsilon
Sampling probability:
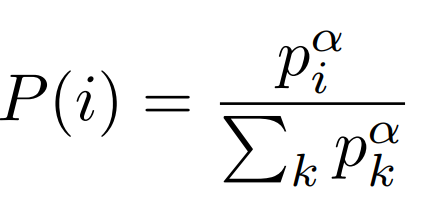
rank-based prioritization:
p_i = 1 / \text{rank}(i)
noise to avoid 0. probs
should be more stable
\(\alpha\) controls randomness
Prioritized Experience Replay
Problem:
- We are estimating mean expected return!
- ...but prioritized replay introduces bias to our estimate!
S,A
S'',A''
S',A'
prob=0.5
High TD-Error:
\(r + \gamma Q(S',A') - Q(S,A)\)
prob=0.5
Low TD-Error:
\(r + \gamma Q(S'',A'') - Q(S,A)\)
\textcolor{red}{prob=0.1}
\textcolor{red}{prob=0.9}
Prioritized Experience Replay
Answer: Fix biased sampling with Importance Sampling
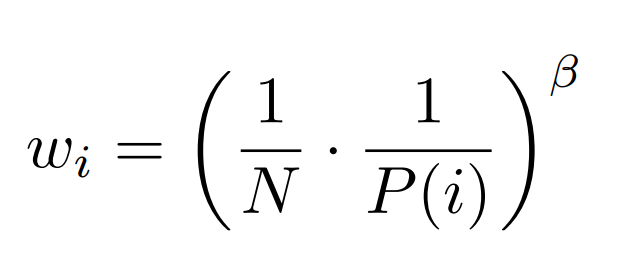
Importance sampling weights:
Here:
- N - Replay Buffer Size
- \(P(i)\) - Sampling Prob
- \(\beta\) - hyperparameter
Normalize \(w_i\) by \(1/max_j w_j\) to avoid increasing learning step size
Use IS weights as coefficient to TD-Error in gradient updates:
\textcolor{red}{w_i} \delta_i \nabla_{\theta} Q_{\theta}(s_i,a_i)
\(\beta\) controls IS correction. Slowly increase \(\beta\) to 1.
already normilized value
Prioritized Experience Replay
Q: How to efficiently sample elements from Replay Buffer proportional to their priority?
A: Use SumTree
non-leaf nodes contains sum of their chidren priorities
Prioritized Experience Replay
SumTree example:
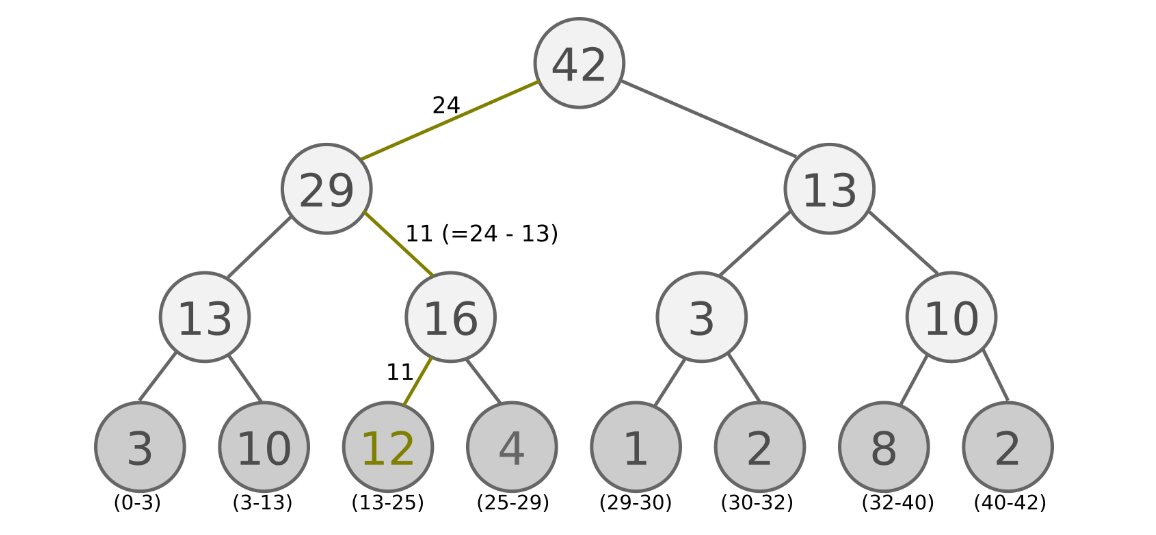
Pseudocode for Sampling:
s = sample random value
node = root
while True:
if s <= p(left_child):
node = left_child
else:
s = s - p(left_child)
node = righ_child
if is_leaf(node): break
Prioritized Experience Replay
Full Algorithm:
Prioritized Experience Replay
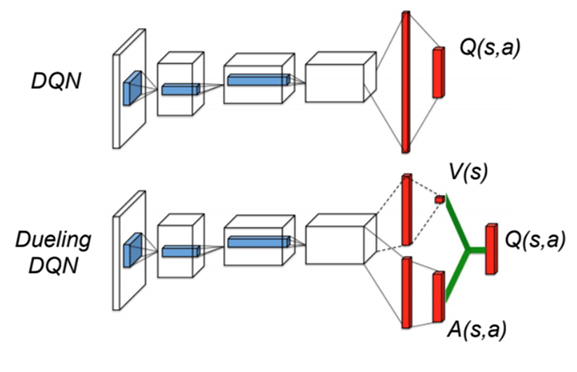
Dueling DQN
Observation:
- Some states are just bad/good regardless of actions
- For policy relative values of actions are more important than their absolute values
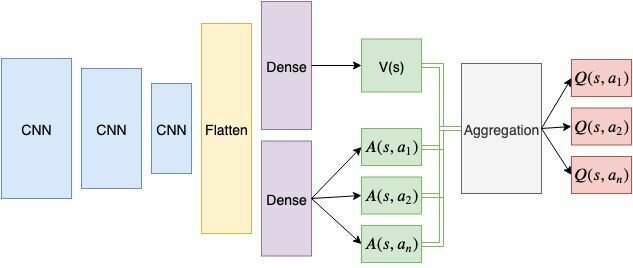
Dueling DQN
Idea:
- Lets estimates States and Actions separately!
Remember Value Functions:
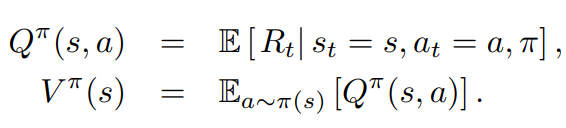
We define Advantage Function:
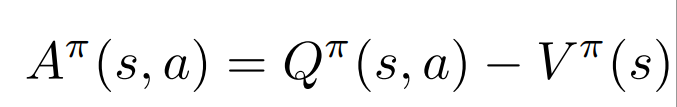
Dueling DQN
Dueling-DQN
DQN
Dueling DQN
Dueling-DQN
Dueling-DQN:
- Aggregate Q-values as: \(Q(s,a) = V(s) + A(s,a)\)
- Learn networks as original DQN
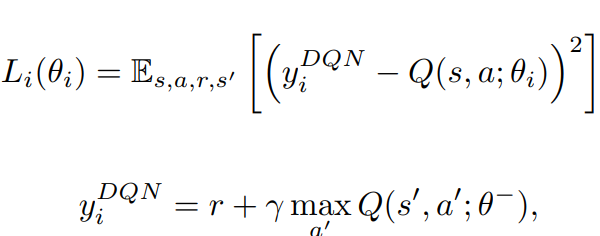
Dueling DQN
But there is a problem with learning from just \(Q\)-values:
Even if the sum \(V(s)+A(s,a)\) is a good estimation,
\(V(s)\) and \(A(s,a)\) can both be incorrect estimates!
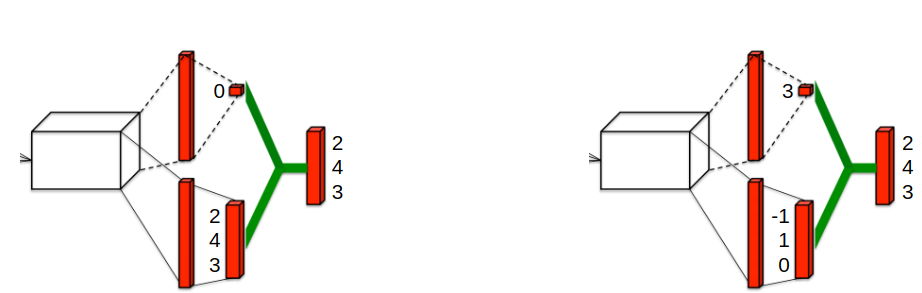
Dueling DQN
Notice the following properties of Advantage functions:
- For a stochastic policy \(\pi(a|s)\):
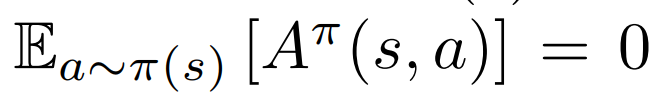
- For greedy deterministic policy \(\pi(s) = argmax_a Q^{*}(s,a) \), where \(a^{*}\) is a greedy action:
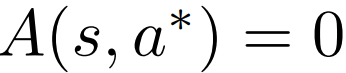
We can force these properties on our Advantage values!
V^{\pi}(s) = \mathbb{E}_{a \sim \pi}[Q^{\pi}(s,a)] \\
= \mathbb{E}_{a \sim \pi}[A^{\pi}(s,a) + V^{\pi}(s)]
= \mathbb{E}_{a \sim \pi}[A^{\pi}(s,a)] + V^{\pi}(s)
= 0 + V^{\pi}(s)
\mathbb{E}_{a \sim \pi}[A^{\pi}(s,a)] = A(s, a^*)
Dueling DQN
Q-value aggregation for greedy policy:
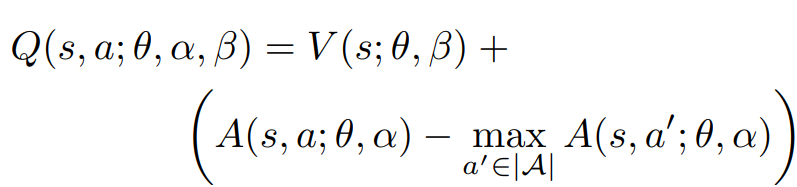
Actual Q-value aggregation in the experiments:
Q-value aggregation for greedy policy:
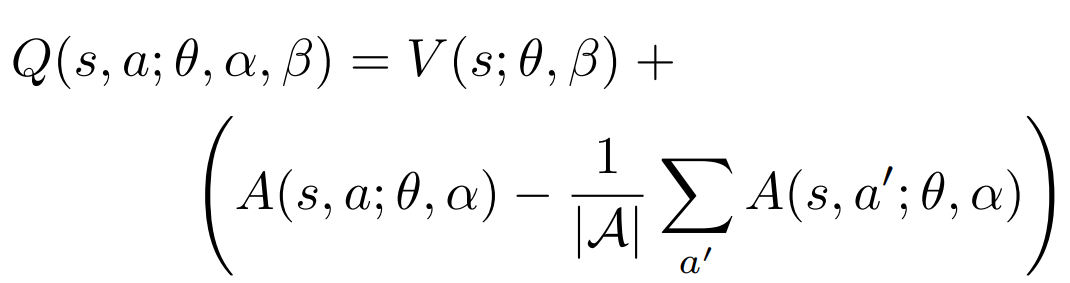
These are just network outputs
Results in brackets are actual advatages!
Dueling DQN
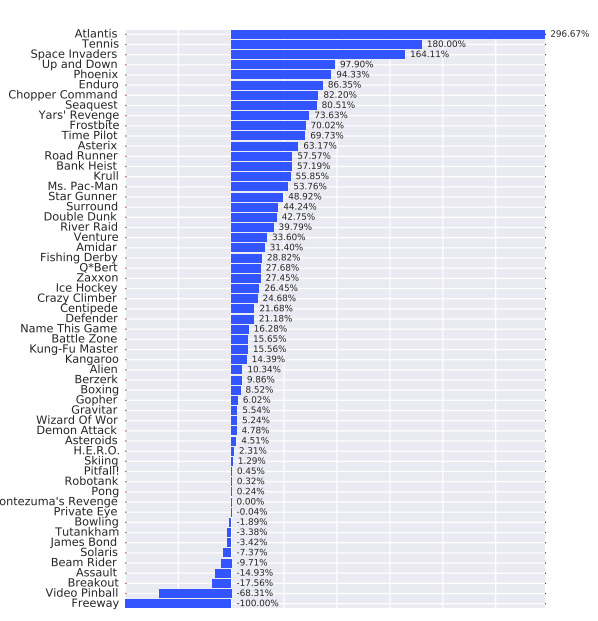
Dueling versus Double
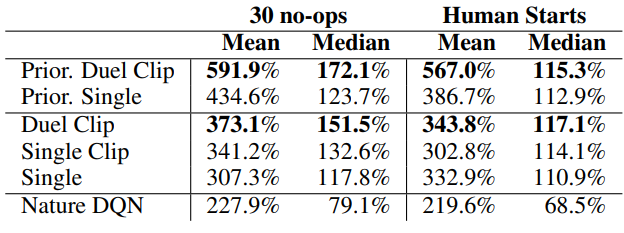
Over all 57 games
Unstructured Exploration Problem
Greedy action:
Exploration action:
NoisyNets for Exploration
Idea: Add noise to network parameters for better exploration!
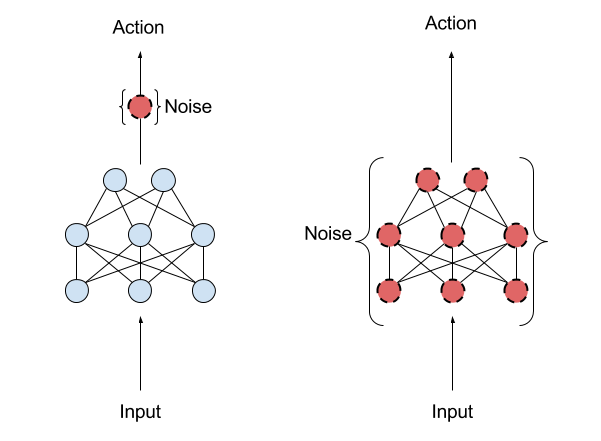
Policy Noise: \(\epsilon\)-greedy
Parameter Noise
NoisyNets for Exploration
Implementation details:
Graphical Representation of Noisy Linear Layer
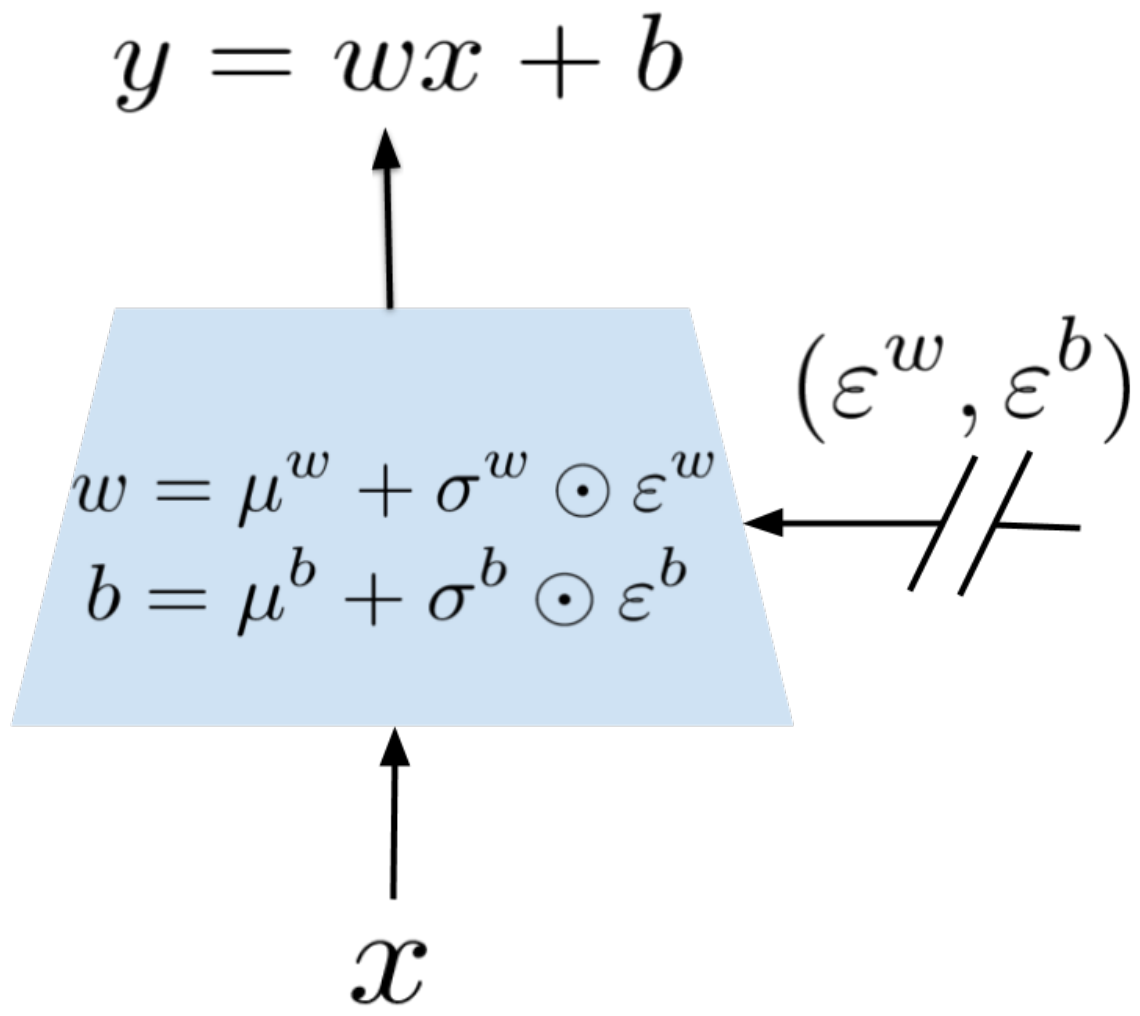
Noise and Parameters:
- \( \mu \)'s and \( \sigma \)'s are learnable parameters!
- \(\epsilon\)'s is a zero-mean noise with fixed statistics
Policy:
- Greedy policy using generated network parameters
- Generate new parameters after each gradient step
NoisyNets for Exploration
Two types of Noise:
-
Independent Gaussian Noise
- You need to generate \(|\text{input}||\text{output}| + |\text{output}|\) values
-
Factored Gaussian Noise
- you generate \(|\text{intput}|\) of \(\epsilon_i\) and \(|\text{output}|\) of \(\epsilon_j\) gaussian variables.
- Then the weight noise is computed as follows:
where
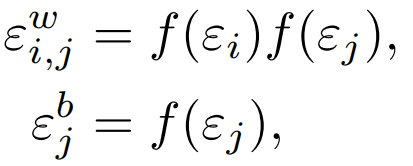
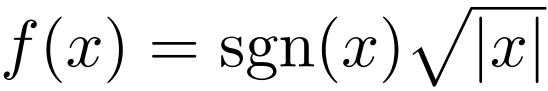
works faster with DQN
used only with Actor-Critic methods
NoisyNets for Exploration
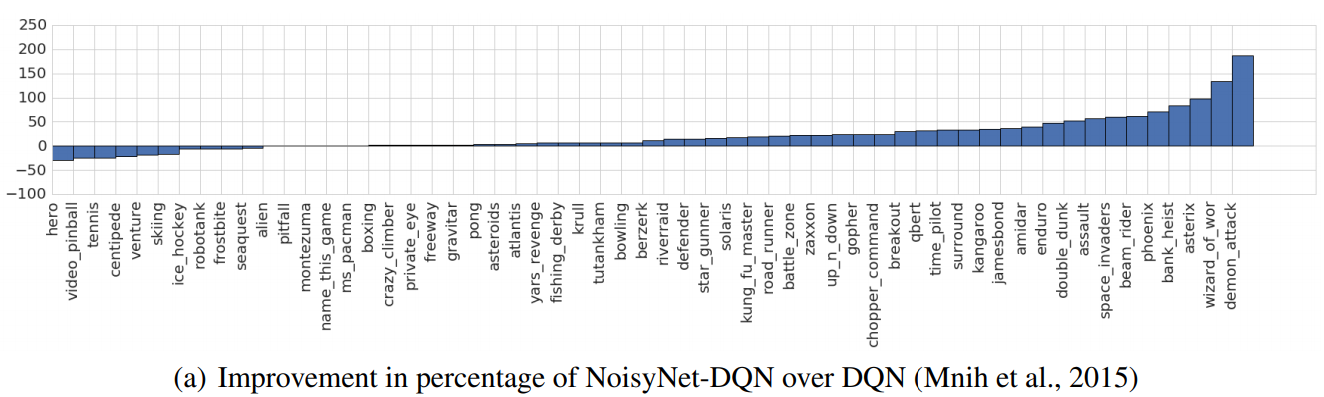
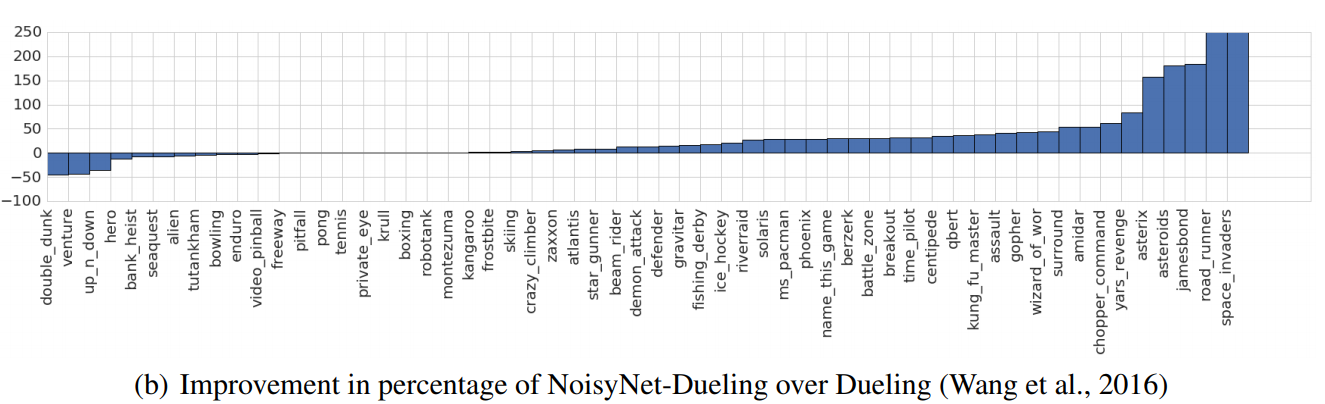
Rainbow: Lets combine everything!
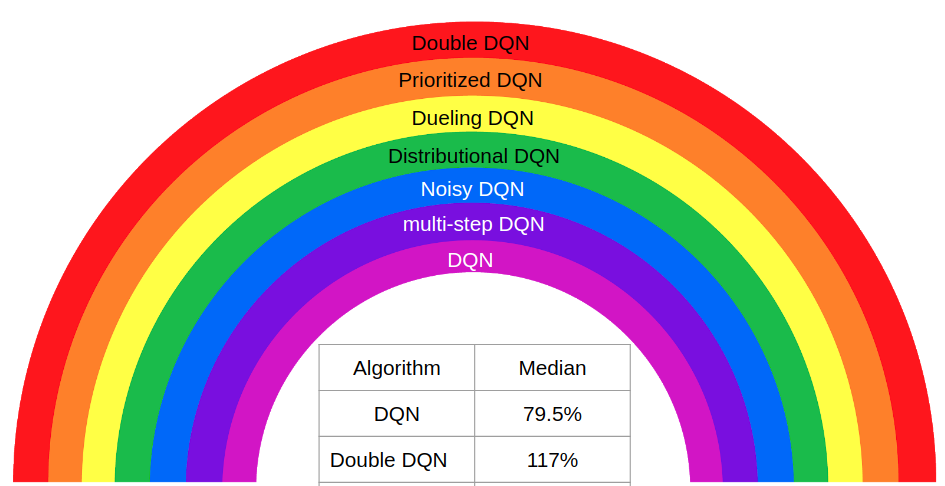
Rainbow: Lets combine everything!
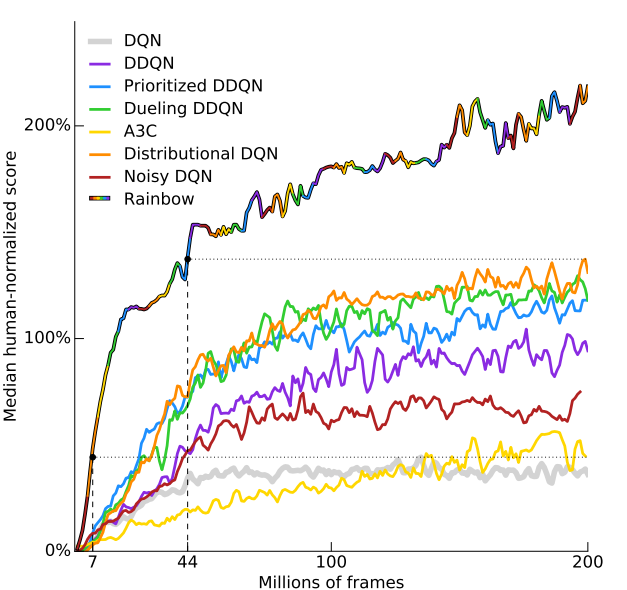
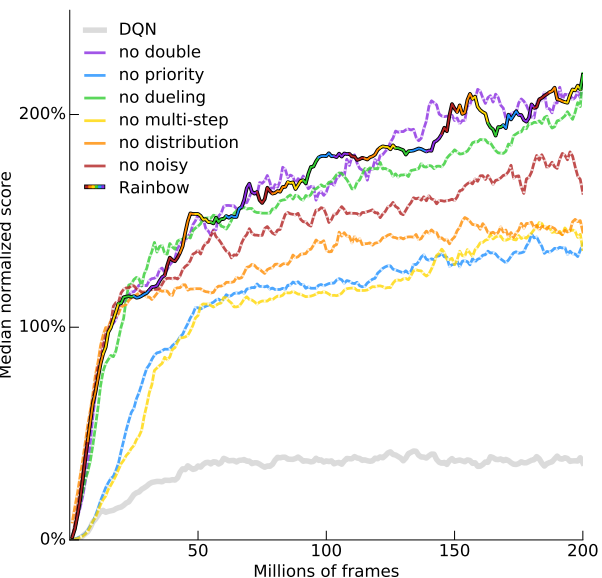
Rainbow: Lets combine everything!
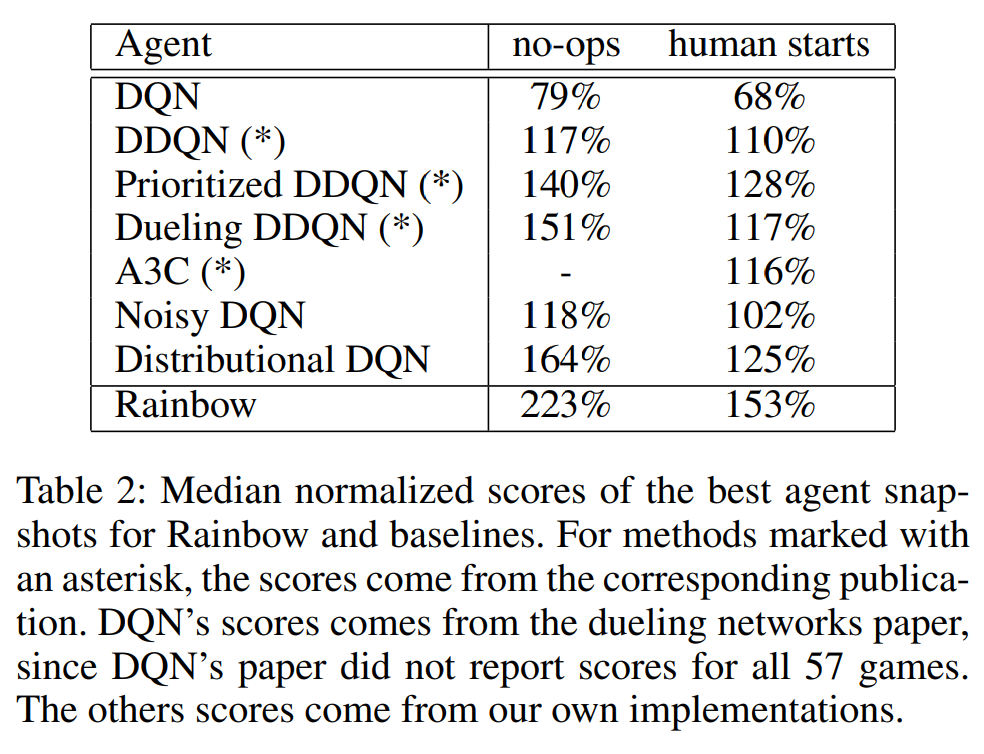
Thank you for your attention!
04 - DQN Versions (seminar)
By supergriver
