Advanced Topics in RL (lecture 12) :
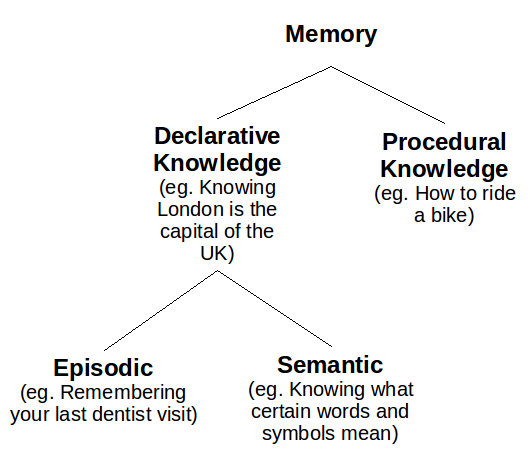
Memory in RL
Artyom Sorokin | 7 May
Markov Decision Process
Basic Theoretical Results in Model-Free Reinforcement Learning are proved for Markov Decision Processes.
Markovian propery:
In other words: "The future is independent of the past given the present."
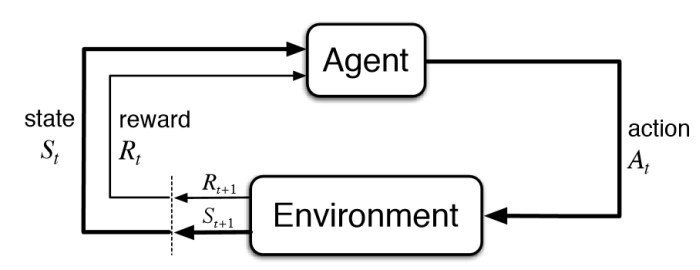
When does agent observe the state?



Partially Observable MDP
Definition
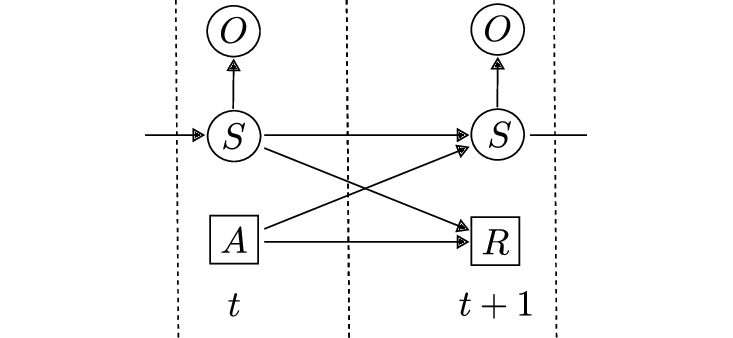
Graphical Model for POMDP:
POMDP is a 6-tuple \(<S,A,R,T,\Omega, O>\):
- \(S\) is a set of states
- \(A\) is a set of actions
- \(R: S \times A \to \mathbb{R}\) is a reward function
- \(T: S \times A \times S \to [0,1]\) is a transition function \(T(s,a,s\prime) = P(S_{t+1}=s\prime|S_t=s, A_t=a)\)
- \(\Omega\) is a set of observations.
- \(O\) is a set of \(|\Omega|\) conditional probability distributions \(P(o|s)\)
Partially Observable MDP
Exact Solution
A proper belief state allows a POMDP to be formulated as a MDP over belief states (Astrom, 1965)
Belief State update:
General Idea:
Belief Update "Beilief" MDP Plan with Value Iteration Policy
Problems:
- Need a model
- Can compute exact belief update only for small/simple MDP
- Can compute Value Iteration only for small MDP
Learning in POMDP
Choose your fighter
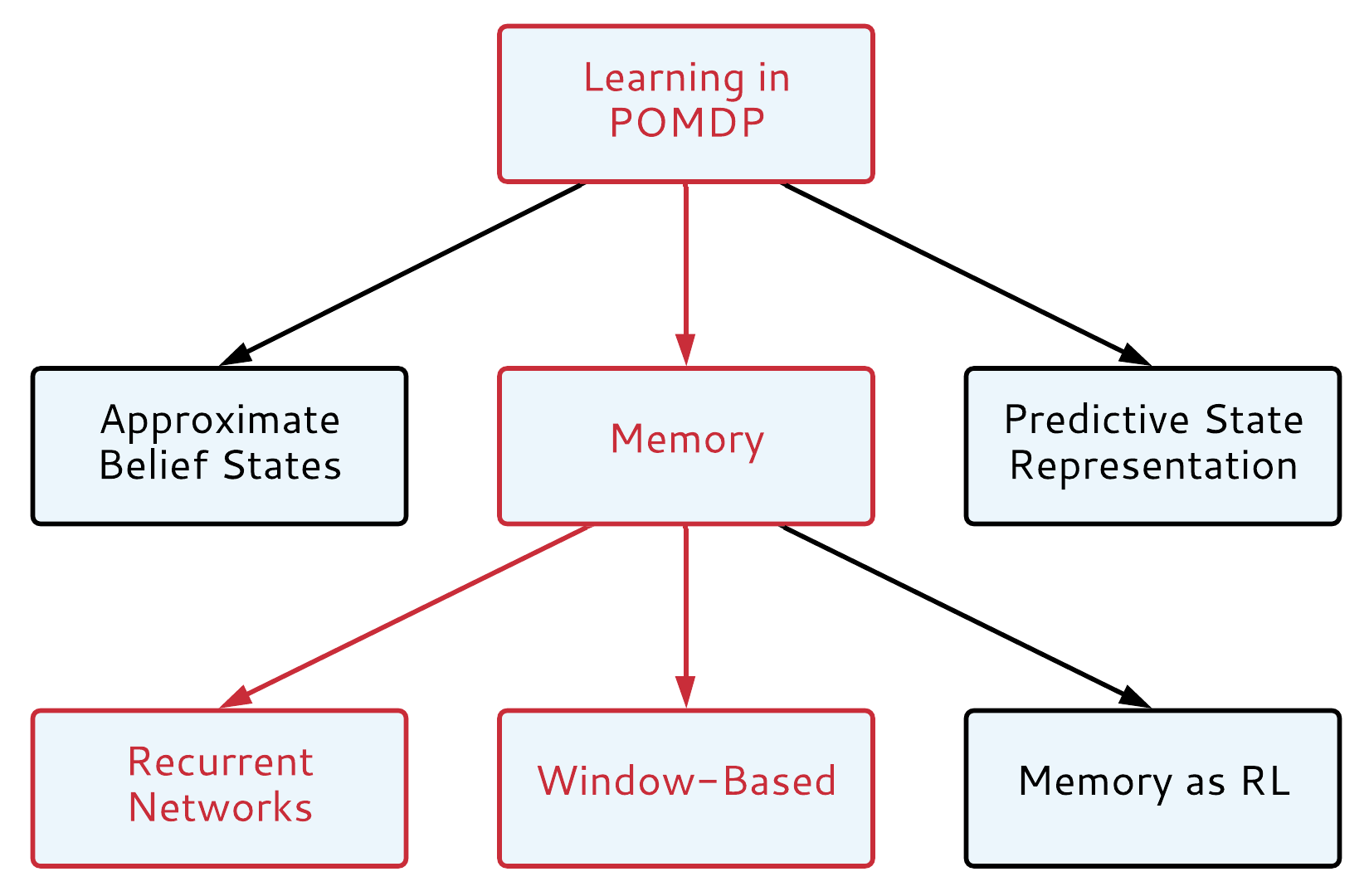
Learning in POMDP
Don't Give Up and Approximate
Approximate belief states:
- Deep Variational Belief Filters(Karl et al, ICLR 2017)
- Deep Variational Reinforcement Learning for POMDPs(Igl et al, ICML 2018)
- Discriminative Particle Filter Reinforcement Learning(Ma et al, ICLR 2020)

(Ma et al, ICLR 2020)
Learning in POMDP
Look into the Future
Predctive State Representations:
- Predictive State Representations (Singh et al, 2004)
- Predictive-State Decoders: Encoding the Future into RNN (Venkatraman et al, NIPS 2017)
- Recurrent Predictive State Policy Networks (Hefny et al, 2018)
Learning in POMDP
Relax and Use Memory
Window-based Memory:
- Control of Memory, Active Perception, and Action in Minecraft (Oh et al, 2016)
- Stabilizing Transformers For Reinforcement Learning (Parisotto et al, 2019)
- Obstacle Tower Challenge winner solution (Nichols, 2019)*
Memory as RL problem:
- Learning Policies with External Memory ( Peshkin et al, 2001)
- Reinforcement Learning Neural Turing Machines (Zaremba et al, 2015)
- Learning Deep NN Policies with Continuous Memory States (Zhang et al, 2015)
Recurrent Neural Networks:
- DRQN (Hausknecht et al, 2015)
- A3C-LSTM (Mnih et al, 2016)
- Neural Map (Parisotto et al, 2017)
- MERLIN (Wayne et al, 2018)
- Relational Recurrent Neural Networks (Santoro et al, 2018)
- Aggregated Memory for Reinforcement Learning (Beck et al, 2020)
Just add LSTM to everything
Off-Policy Learning (DRQN):
- Add LSTM before last 1-2 layers
- Sample sequences of steps from Experience Replay
On-Policy Learning (A3C/PPO):
- Add LSTM before last 1-2 layers
- Keep LSTM hidden state \(h_t\) between rollouts

Asynchronous Methods for Deep Reinforcement Learning (Mnih et al, 2016) | DeepMind, ICML, 3113 citations
Deep Recurrent Q-Learning for Partially Observable MDPs
(Hausknecht et al, 2015) AAAI, 582 citations )
Just add LSTM to everything
Default choice for memory in big projects
"To deal with partial observability, the temporal sequence of observations is processed by a deep long short-term memory (LSTM) system"
AlphaStar Grandmaster level in StarCraft II using multi-agent reinforcement learning (Vinyalis et al, 2019) | DeepMind, Nature, 16 Citations
Just add LSTM to everything
Default choice for memory in big projects
"The LSTM composes 84% of the model’s total parameter count."
Dota 2 with Large Scale Deep Reinforcement Learning (Berner et al, 2019) | OpenAI, 17 Citations
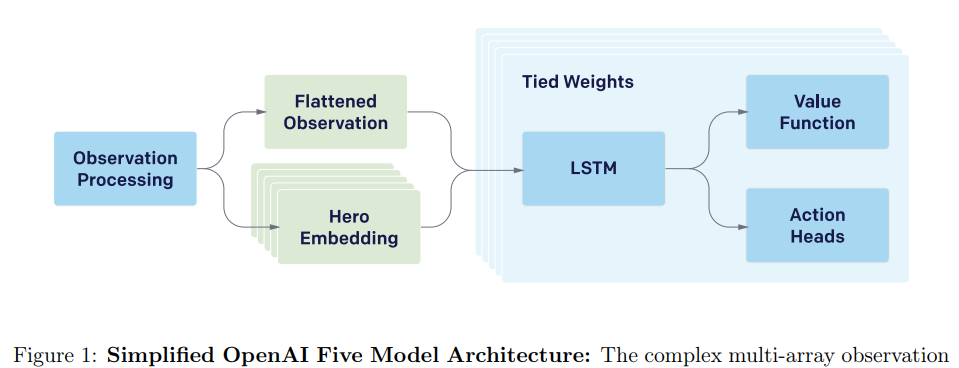
R2D2: We can do better
DRQN tests two sampling methods:
- Sample full episode sequences
- Problem: sample correlation in mini-batch is proportional to the sequence length
- Sample random sub-sequences of length k (10 steps in the paper)
- Problem: initial hidden state is zero at the start of a rollout
Recurrent Experience Replay in Distributed Reinforcement Learning (Kapturowski et al, 2019) | DeepMind, ICLR, 49 citations
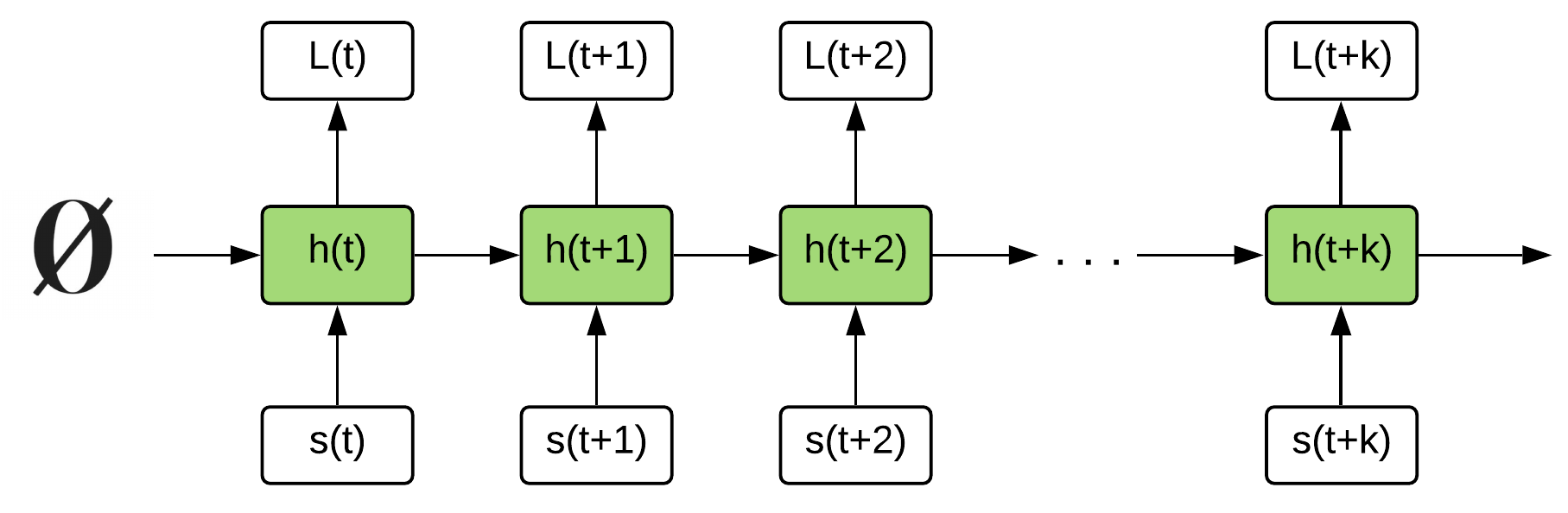
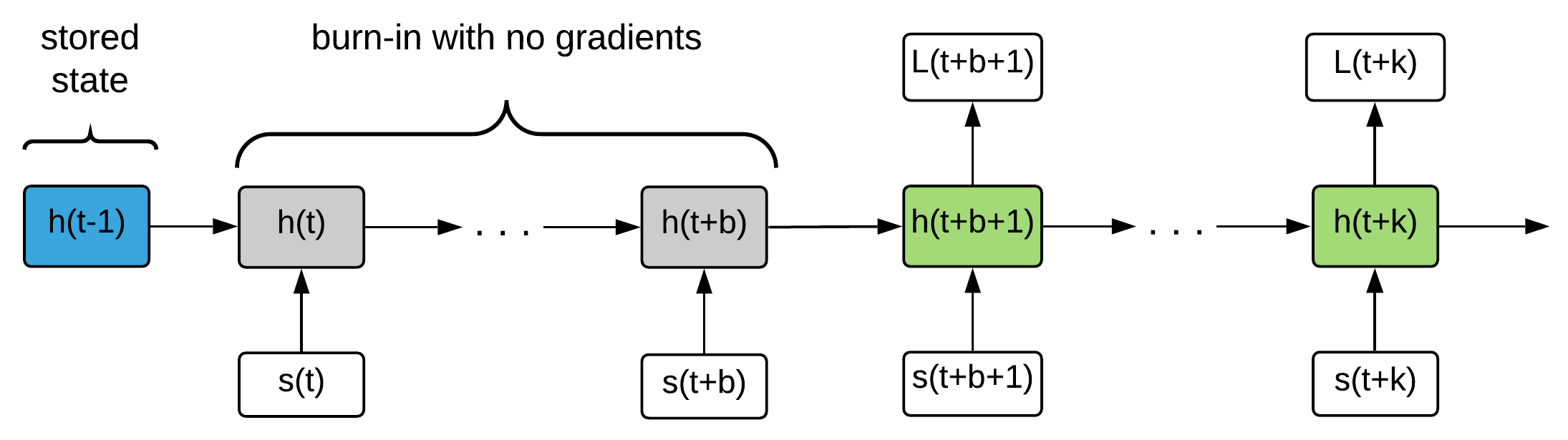
R2D2: We can do better
R2D2 is a DRQN build on top of Ape-X (Horgan et al, 2018) with addition of two heuristics:
- Stored state: Storing the recurrent state in replay and using it to initialize the network at training time
- Burn-in: Use a portion of the replay sequence only for unrolling the network and producing a start state, and update the network only on the remaining part of the sequence
Burn-in - 40 steps, full rollout - 80 steps
Recurrent Experience Replay in Distributed Reinforcement Learning (Kapturowski et al, 2019) | DeepMind, ICLR, 49 citations
R2D2
Results: Atari-57
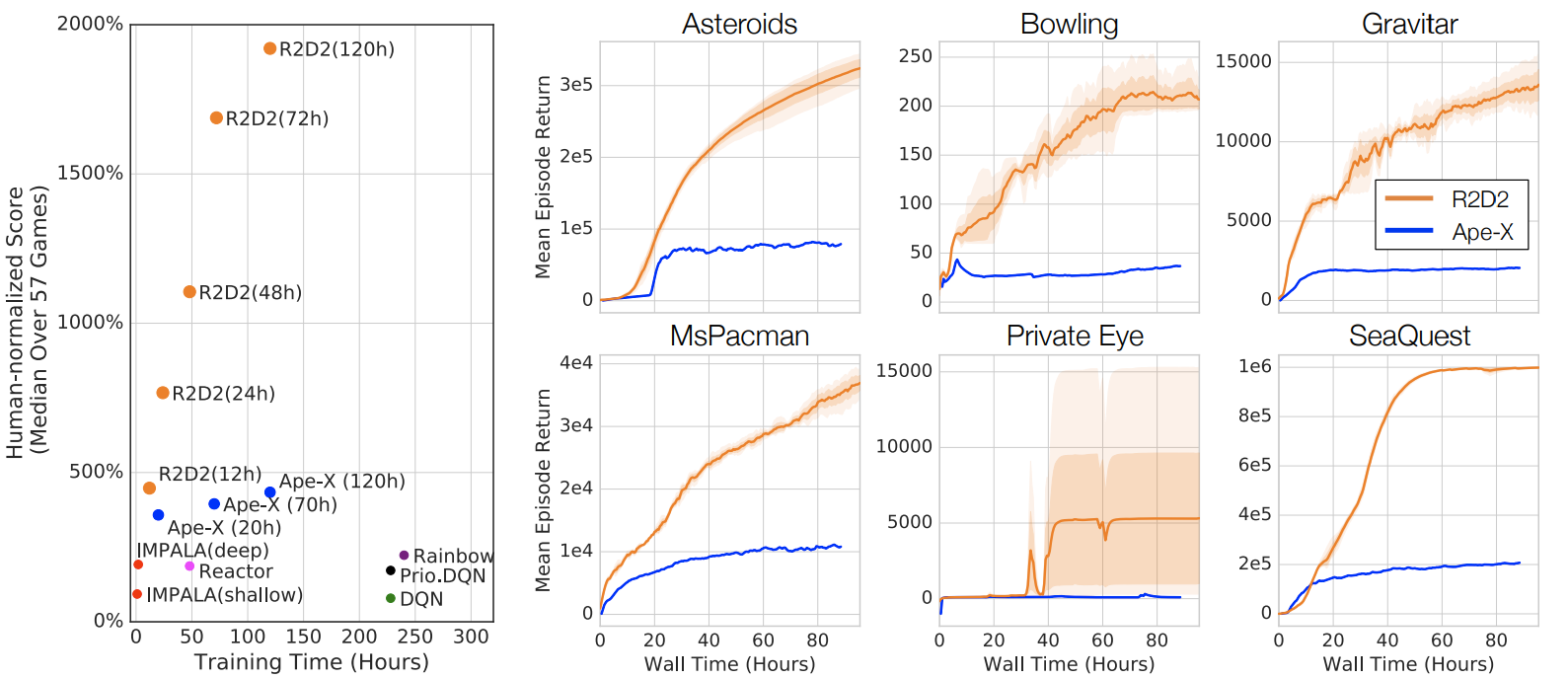
R2D2
Results: DMLab-30
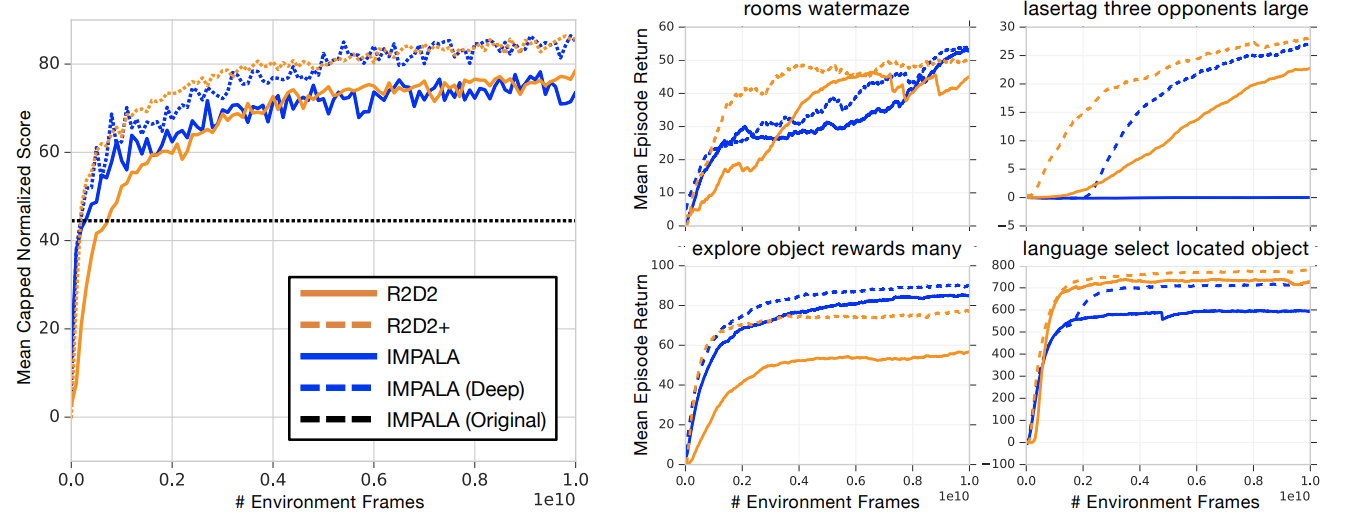
Recurrent Experience Replay in Distributed Reinforcement Learning (Kapturowski et al, 2019) | DeepMind, ICLR, 49 citations
AMRL
Motivation
Recurrent Neural Networks:
-
good at tracking order of observations
-
susceptible to noise in observations
-
bad at long-term dependencies
RL Tasks:
-
order often doesn't matter
-
high variability in observation sequences
-
long-term dependencies
AMRL: Aggregated Memory For Reinforcement Learning (2020) | MS Research, ICLR
AMRL:
Robust Aggregators
Add aggregators that ignore order of observations: Agregators also act as residual skip connections across time. Instead of true gradients a straight-through estimator(Bengio et al., 2013) is used.
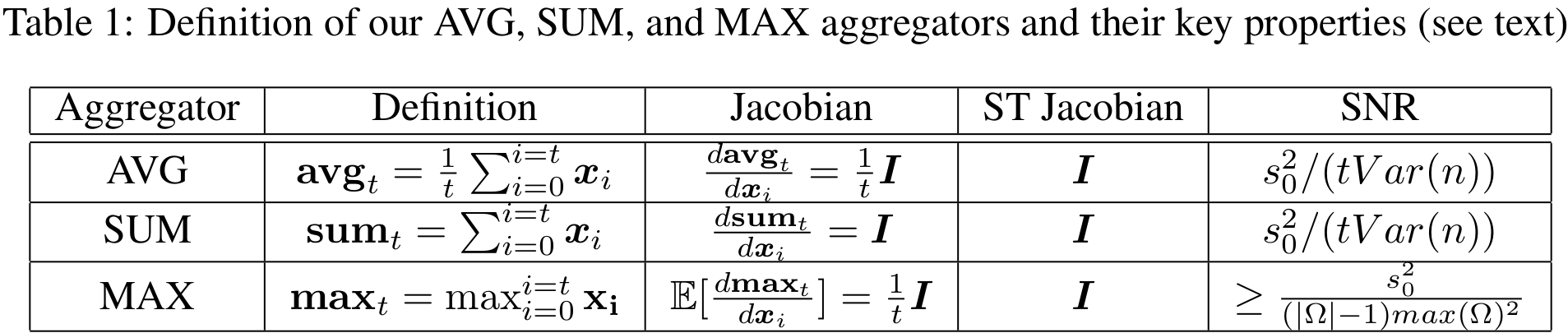
AMRL: Aggregated Memory For Reinforcement Learning (2020) | MS Research, ICLR
AMRL
Architecture and Baselines
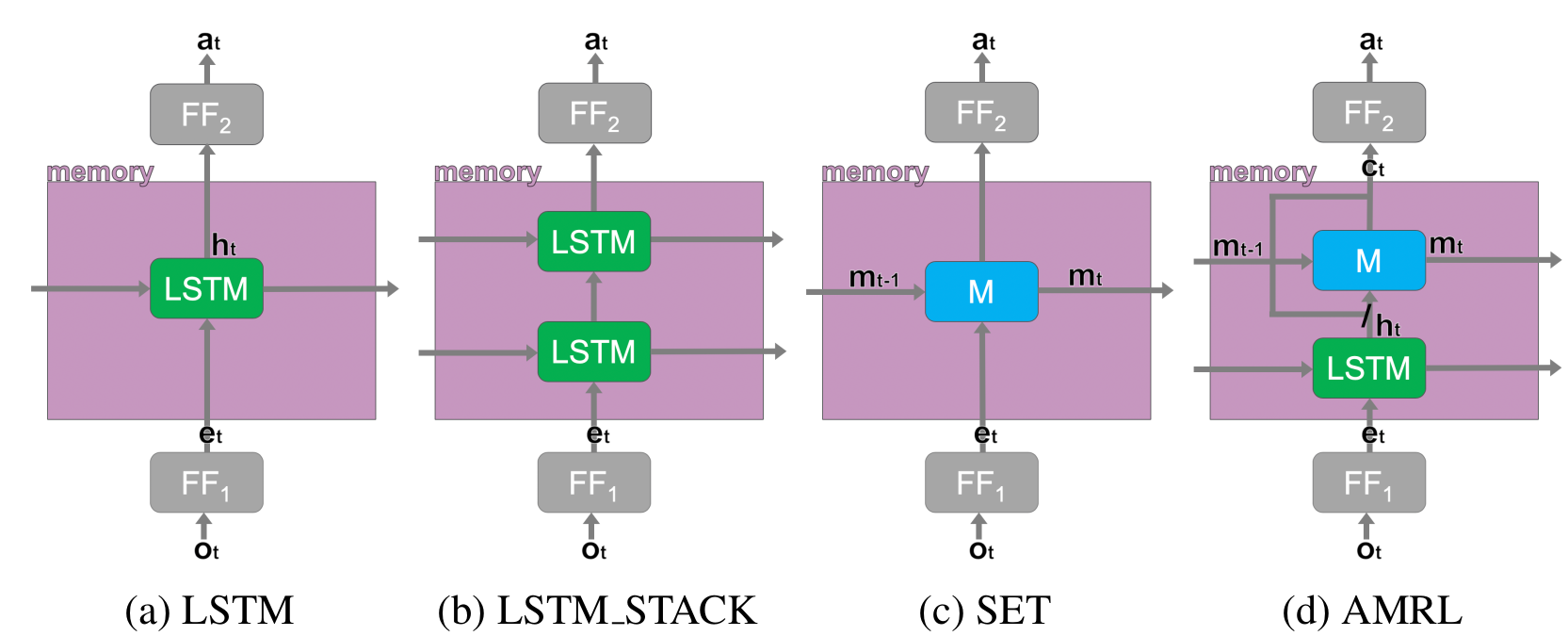
AMRL: Aggregated Memory For Reinforcement Learning (2020) | MS Research, ICLR
AMRL
Experiments

AMRL: Aggregated Memory For Reinforcement Learning (2020) | MS Research, ICLR
AMRL
Experiments
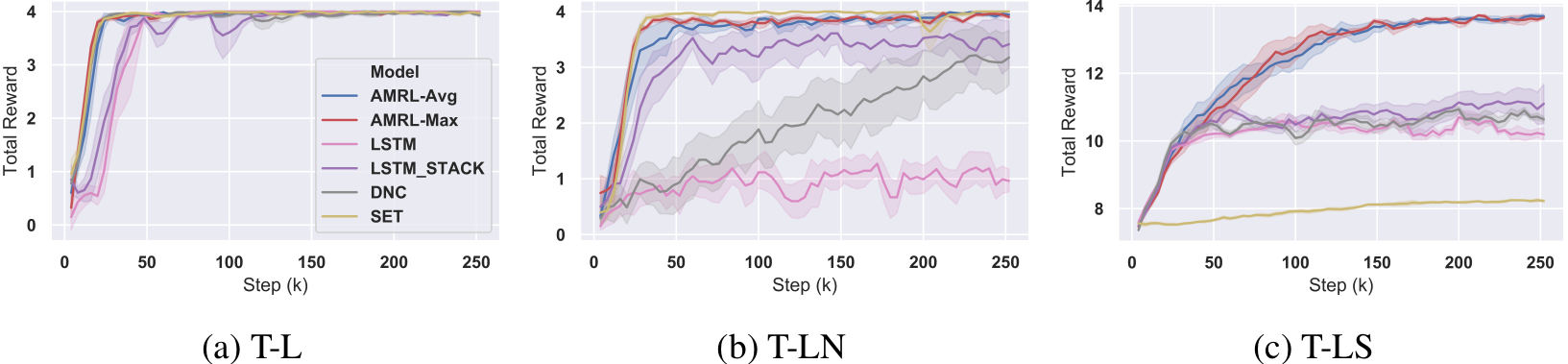
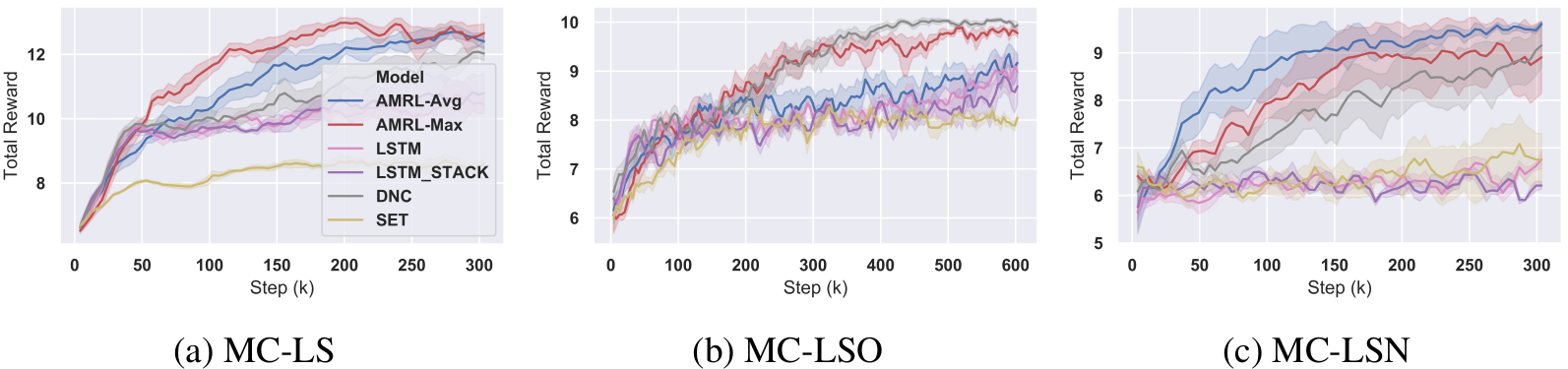
AMRL
Experiments
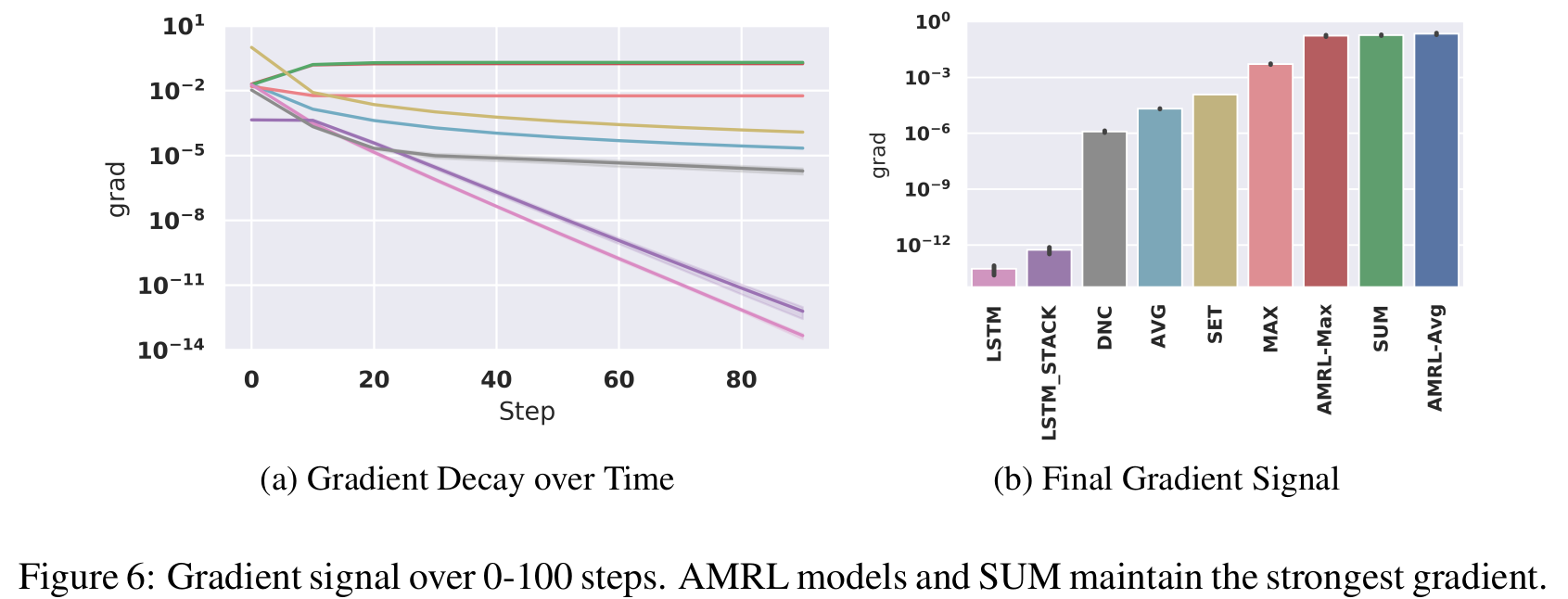
AMRL: Aggregated Memory For Reinforcement Learning (2020) | MS Research, ICLR
Are rewards enough to learn memory?
-
Learning only by optimizing future rewards
-
A3C/PPO + LSTM
- DRQN, R2D2
- AMRL
-
-
What if we know a little bit more?
- Neural Map (Parisotto et al, 2017)
- Working Memory Graphs(Loynd et al, 2020,)
-
Learing with rich self-supervised sensory signals
- World Models (Ha et al, 2018, Mar 27*)
- MERLIN (Wayne et al, 2018, Mar 28*)
MERLIN
Unsupervised Predictive Memory in a Goal-Directed Agent (2018) | DeepMind, 67 citations
MERLIN has two basic components:
-
Model-Based Predictor
a monstrous combination of VAE and Q-function estimator
uses simplified DNC under the hood
-
Policy
no gradients flow between policy and MBR
trained with Policy Gradients and GAE
MERLIN is trained on-policy in A3C-like manner:
- 192 parallel workers, 1 parameter server
- rollout length is 20-24 steps
MERLIN
Architecture
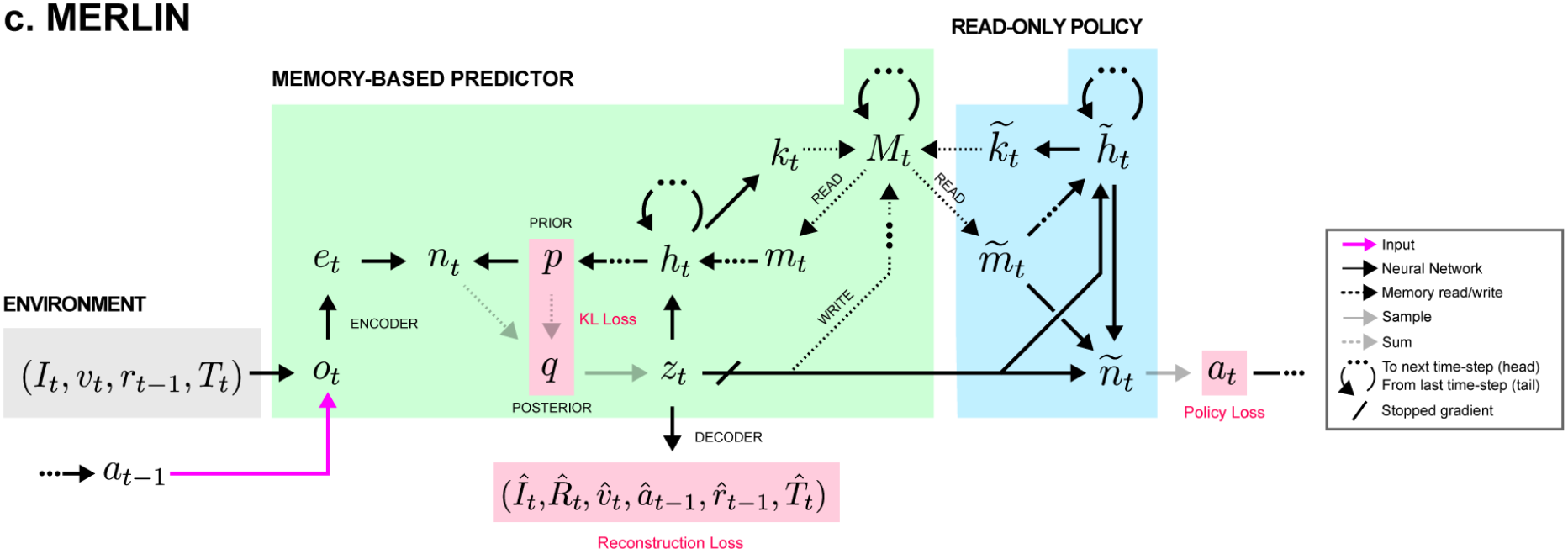
Unsupervised Predictive Memory in a Goal-Directed Agent (2018) | DeepMind, 67 citations
MERLIN
Memory-Based Predictor
Prior Distribution
Module takes all memory from the previous step and produces parameters of Diagonal Gaussian distribution:
Posterior Distribution
Another MLP \(f^{post}\) takes:
and generates correction for the prior:
At the end, latent state variable \(z_t\) is sampled from posterior distribution.
MERLIN
MBR Loss
Model-Based Predictor has a loss function based on the variational lower bound:
Reconstruction Loss: KL Loss:
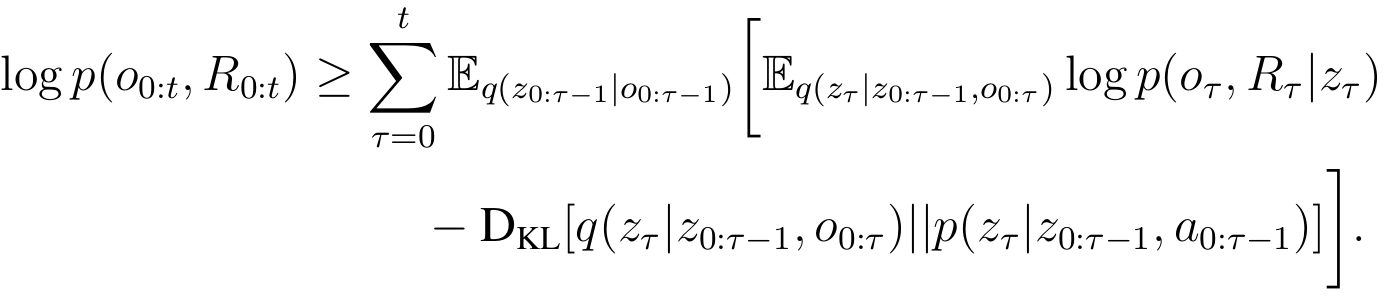
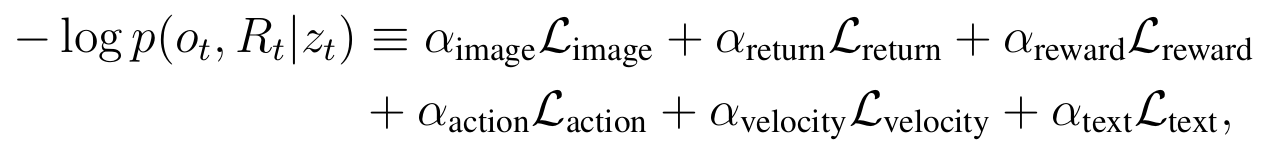
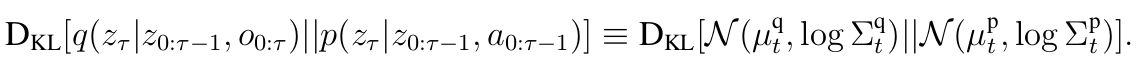
MERLIN
Experiments
MERLIN is compared against two baselines: A3C-LSTM, A3C-DNC
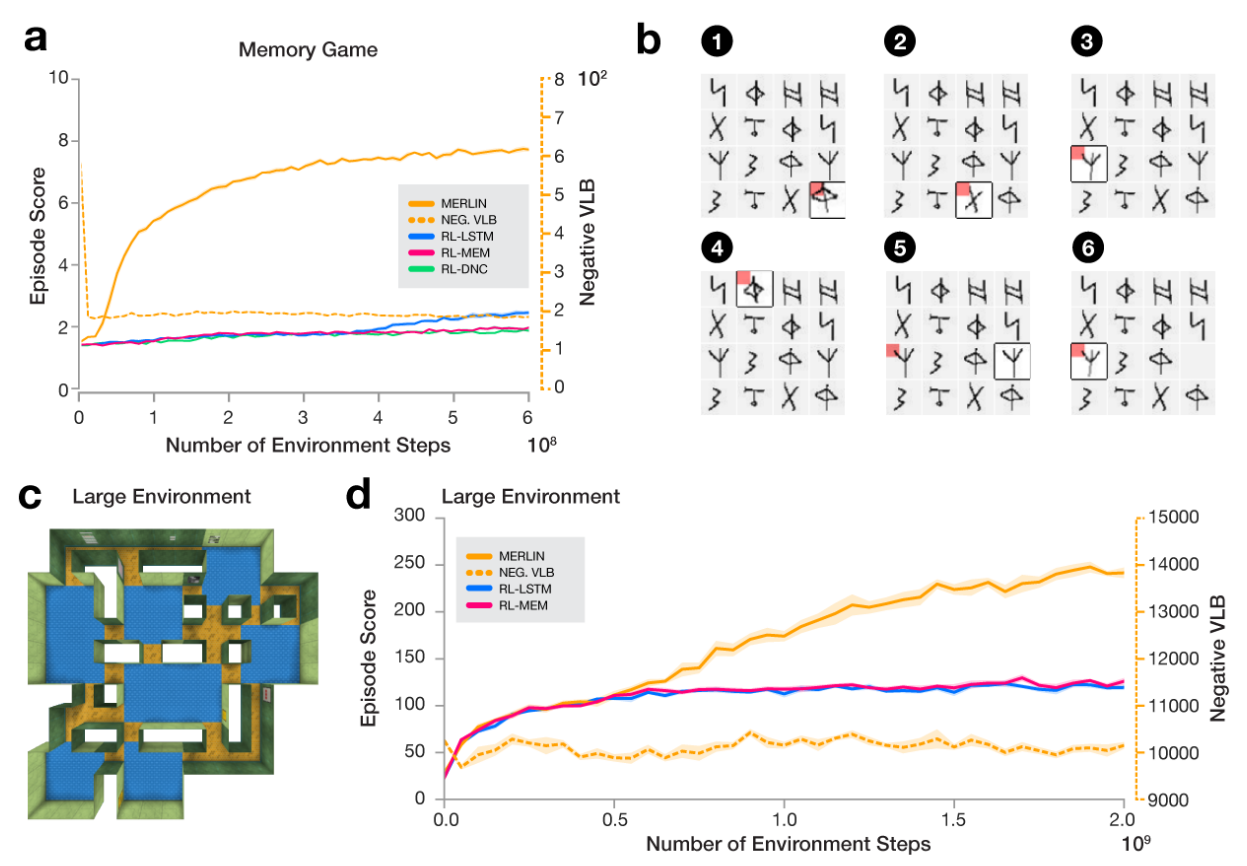
MERLIN
Experiments
Unsupervised Predictive Memory in a Goal-Directed Agent (2018) | DeepMind, 67 citations
Stabilizing Transformers for RL
Stabilizing Transformers For Reinforcement Learning (2019) | DeepMind
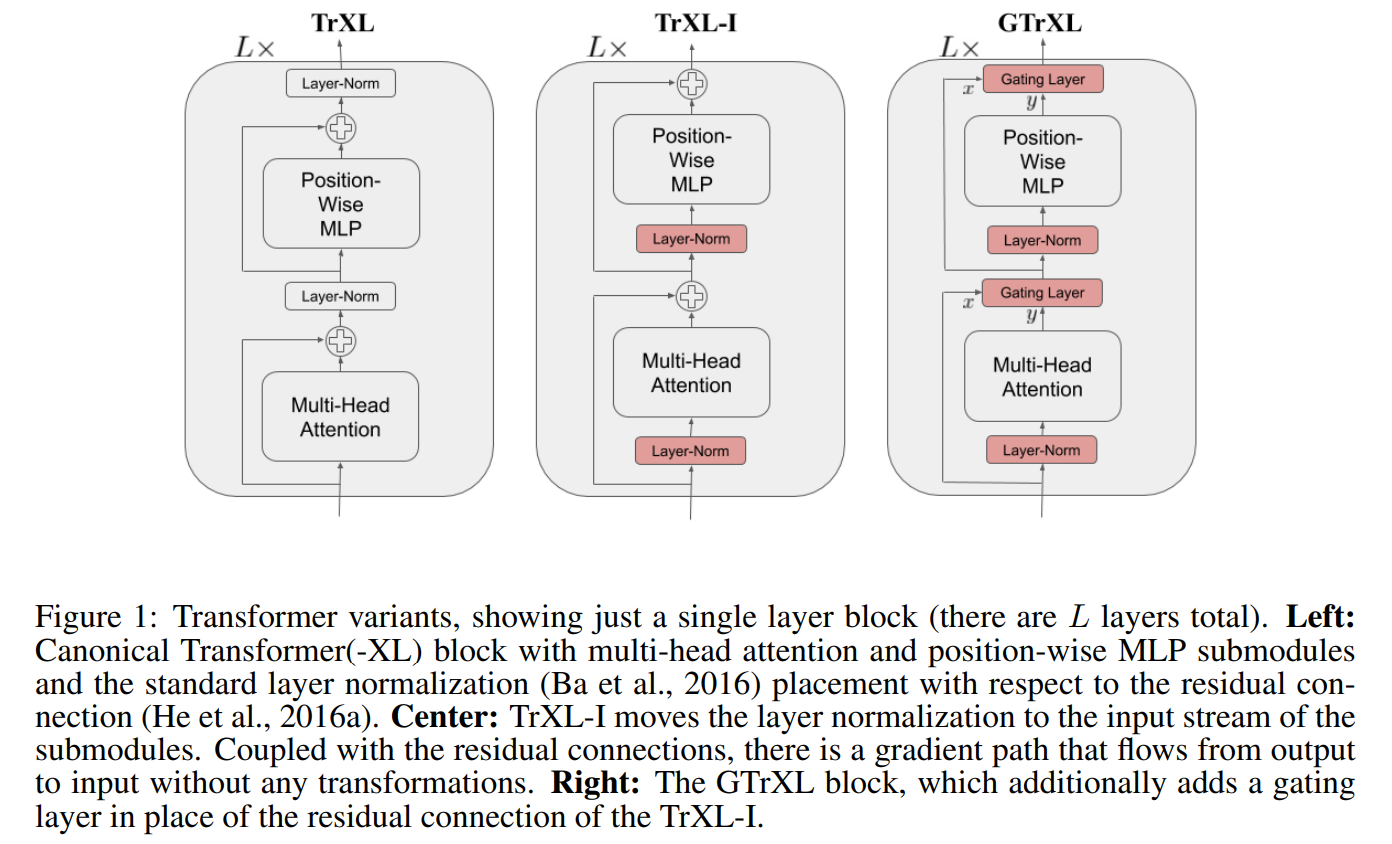
Stabilizing Transformers for RL
Gating Layer
Stabilizing Transformers For Reinforcement Learning (2019) | DeepMind

Stabilizing Transformers for RL
Experiments
Stabilizing Transformers For Reinforcement Learning (2019) | DeepMind
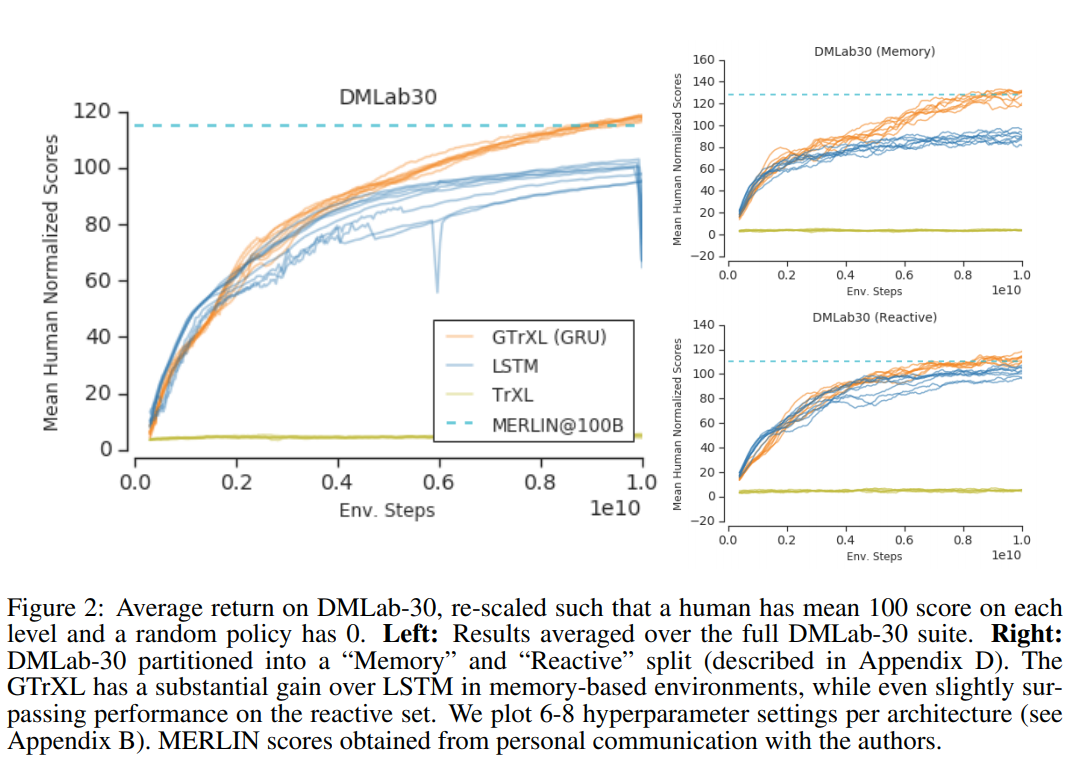
Stabilizing Transformers for RL
Ablation Study
Stabilizing Transformers For Reinforcement Learning (2019) | DeepMind

Memory for MDP?
-
Remembering a simple pattern could be easier than recognizing a hard pattern on the fly
-
Neural Networks can't adapt fast:
-
Catastrophic interference i.e knowledge in neural networks is non-local
-
Nature of gradients
-
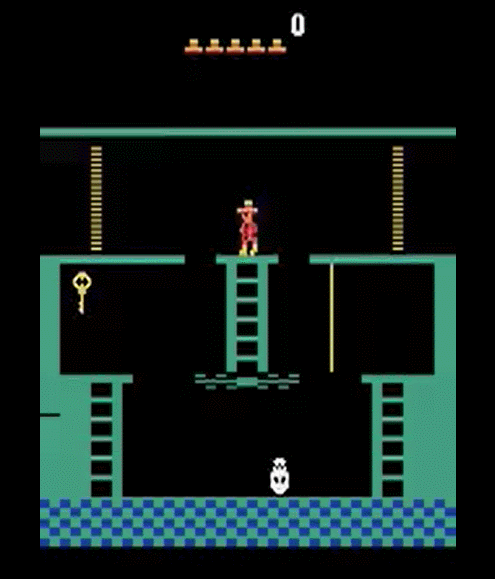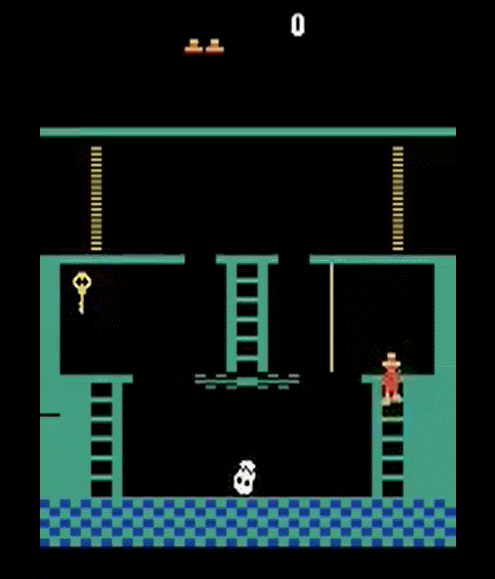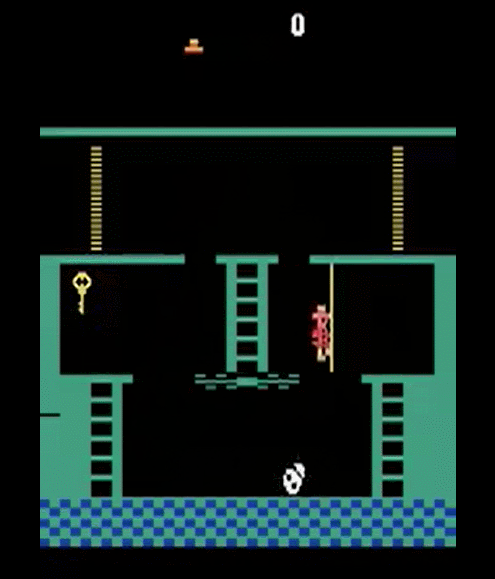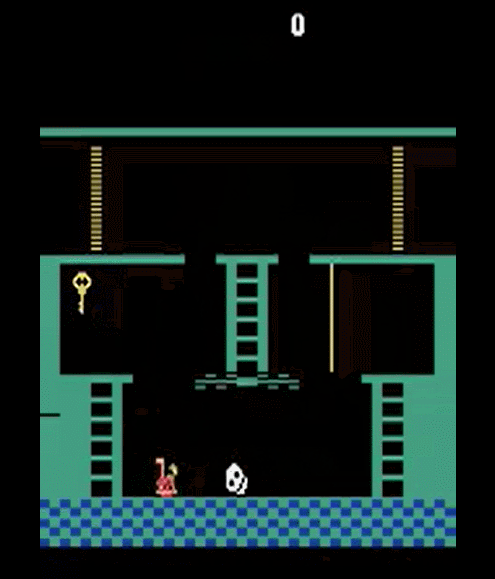
Episodic Memory
Motivation
Semantic memory makes better use of experiences (i.e. better generalization)
Episodic memory requires fewer experiences (i.e. more accurate)
Episodic Memory
Experiment with Tree MDP
"We will show that in general, just as model-free control is better than model-based control after substantial experience, episodic control is better than model-based control after only very limited experience."
A Tree MDP is just a MPD without circles.
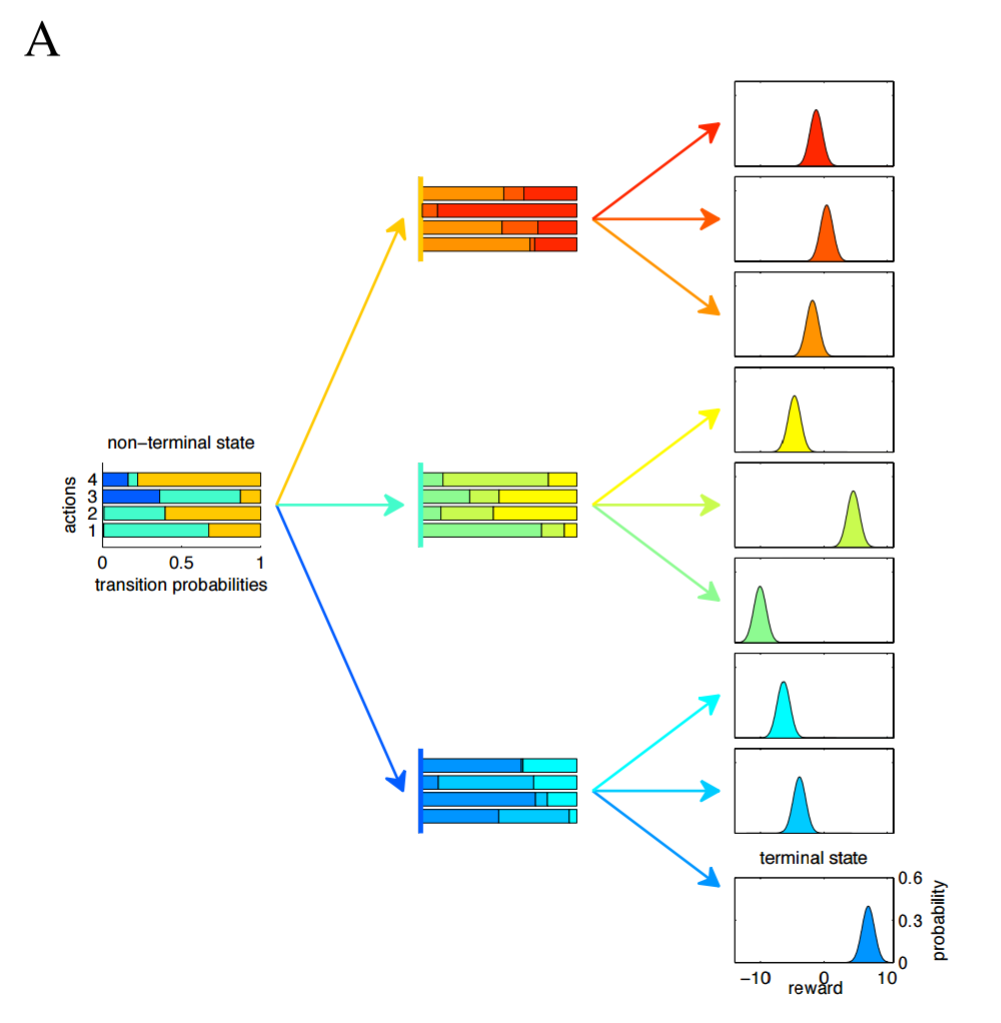
Episodic Memory
Experiment with Tree MDP
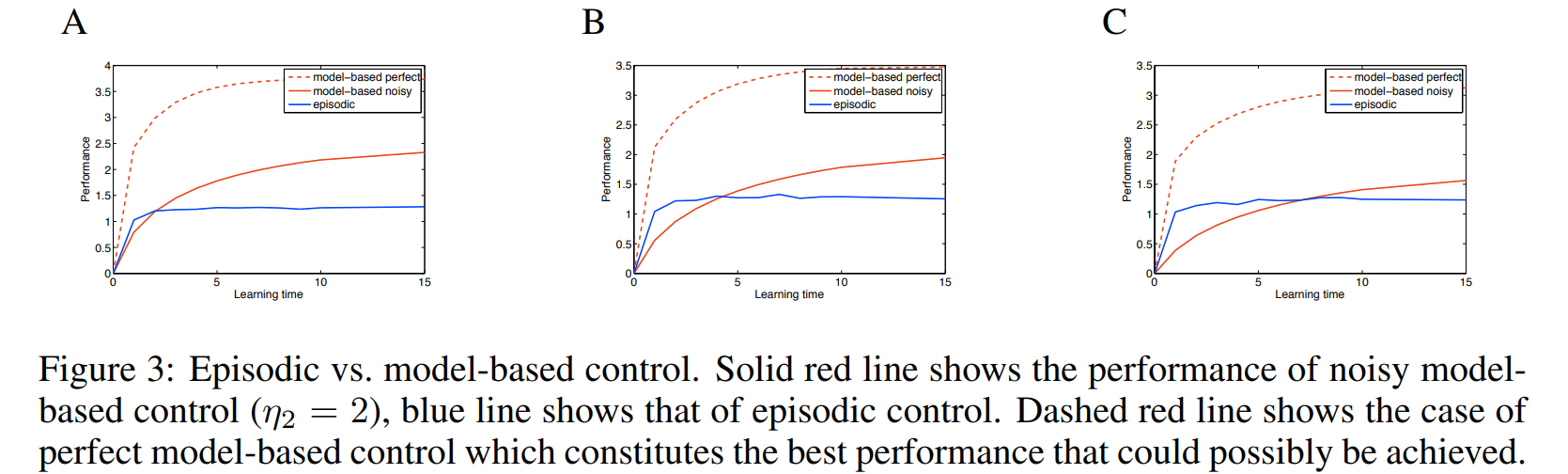
Text
Text
A) Tree MDP with branching factor = 2 B) Tree MDP with branching factor = 3 C) Tree MDP with branching factor = 4
Model-Free Episodic Control
Lets store all past experiences in \(|A|\) dictionaries \(Q_{a}^{EC} \)
\(s_t, a_t \) are keys and discounted future rewards \(R_t\) are values.
Dictionary update:
If a state space has a meaningful distance, then we can use k-nearest neightbours to estimate new \((s,a)\) pairs:
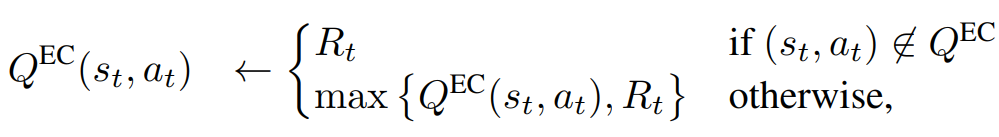
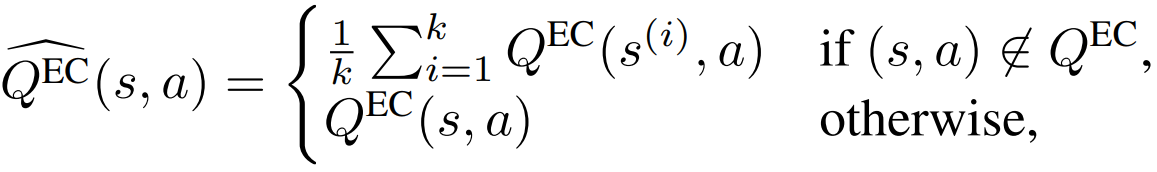
Model-Free Episodic Control (2016) | DeepMind, 100 citations
Model-Free Episodic Control
Lets store all past experiences in \(|A|\) dictionaries \(Q_{a}^{EC} \)
\(s_t, a_t \) are keys and discounted future rewards \(R_t\) are values.
Dictionary update:
If a state space has a meaningful distance, then we can use k-nearest neightbours to estimate new \((s,a)\) pairs:
Two possible feature compressors for \(s_t\): Random Network, VAE
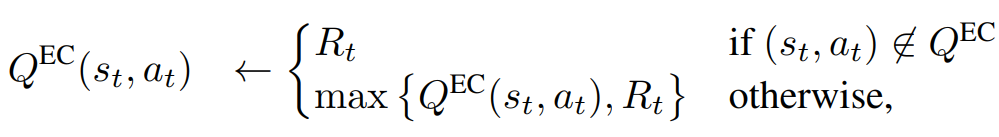
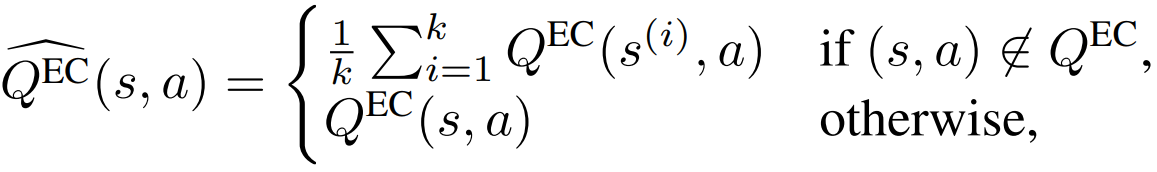
Model Free Episodic Control
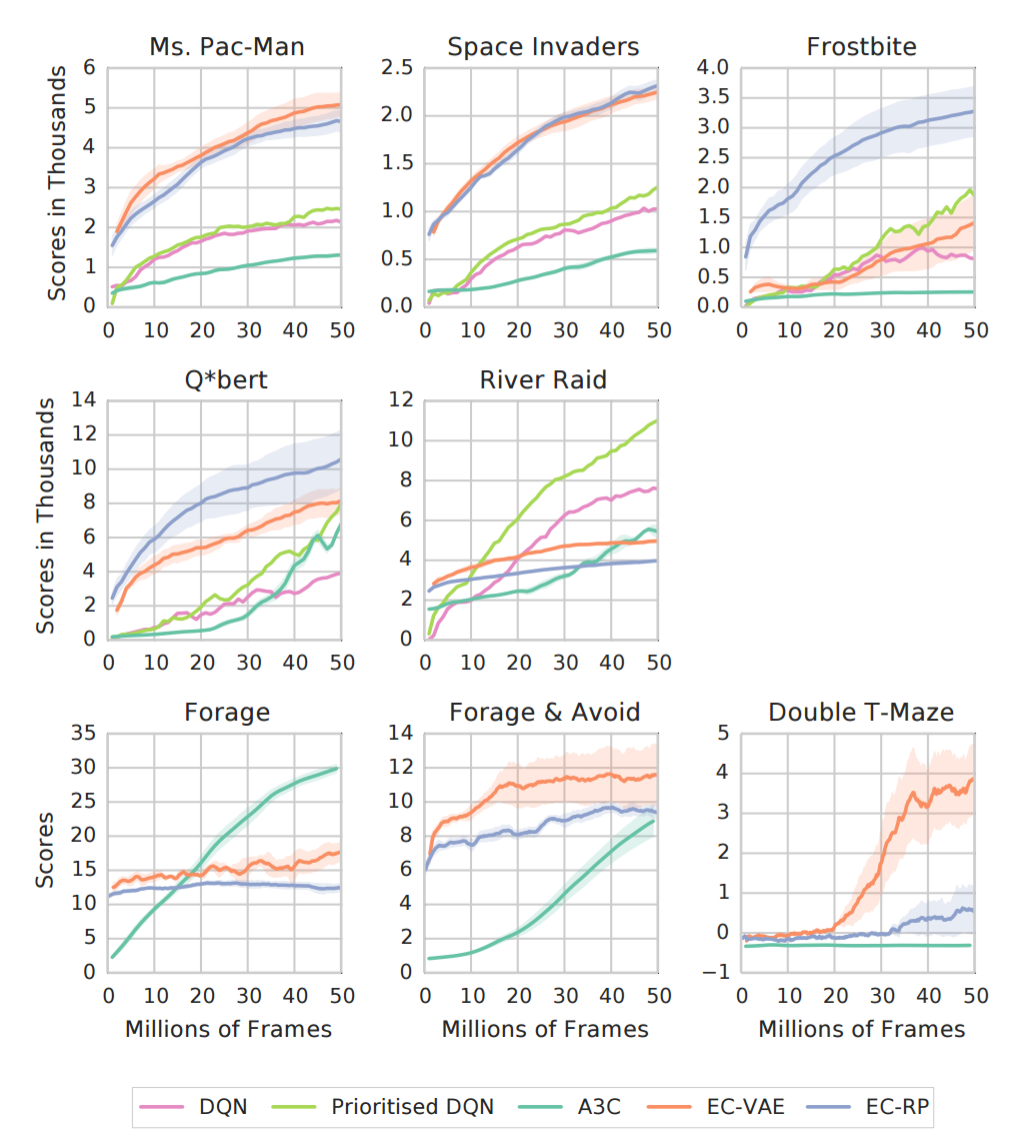
Results
Test environments:
- Some games from Atari 57
- 3D Mazes in DMLab
Neural Episodic Control
Deep RL + Semantic Memory
Differences with Model-Free Episodic Control:
-
CNN instead of VAE/RandomNet
-
Differential Neural Dictionaries (DND)
-
Replay Memory like in DQN, but small...
-
CNN and DND learn with gradient descent
Neural Episodic Control (2016) | DeepMind, 115 citations
Neural Episodic Control
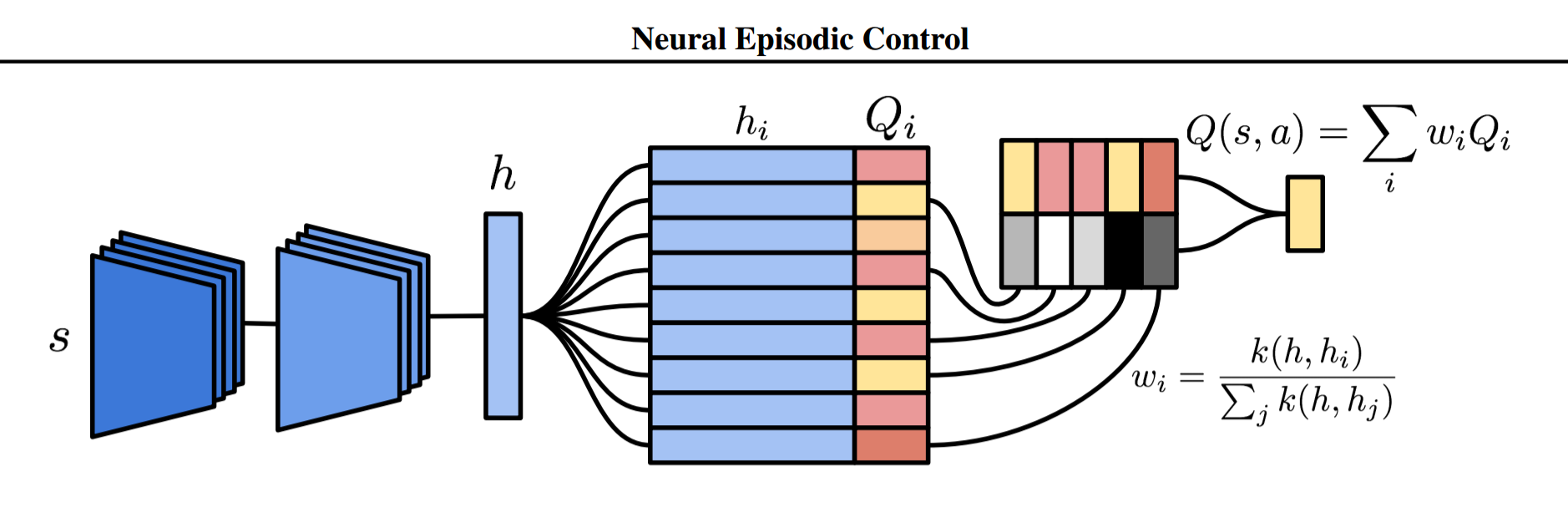
Differential Neural Dictionaries
For each action \(a \in A \), NEC has a dictionary \(M_a = (K_a , V_a )\).
Keys and Queries are generated by CNN
Neural Episodic Control
Differential Neural Dictionaries
To estimate \(Q(s_t, a)\) we sample p-nearest neighbors from \(M_a\)
\(k\) is a kernel for distance estimate. In experiments:

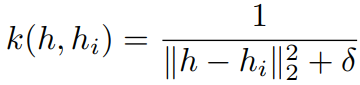
Neural Episodic Control
DND Update
Once a key \(h_t\) is queried from a DND, that key and its corresponding output are appended to the DND. If \(h_t \in M_a\) then we just store it with N-step Q-value estimate:
otherwise, we update stored value with tabular Q-learning rule:
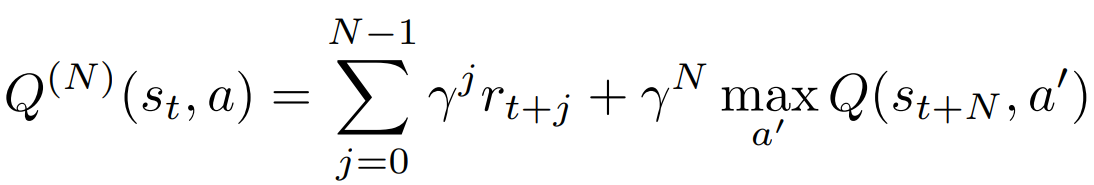

Learn DND and CNN-encoder:
Sample mini-batches from replay buffer that stores triplets \((s_t,a_t, R_t)\) and use \(R_t\) as a target.
Neural Episodic Control (2016) | DeepMind, 115 citations
Neural Episodic Control
Experiments
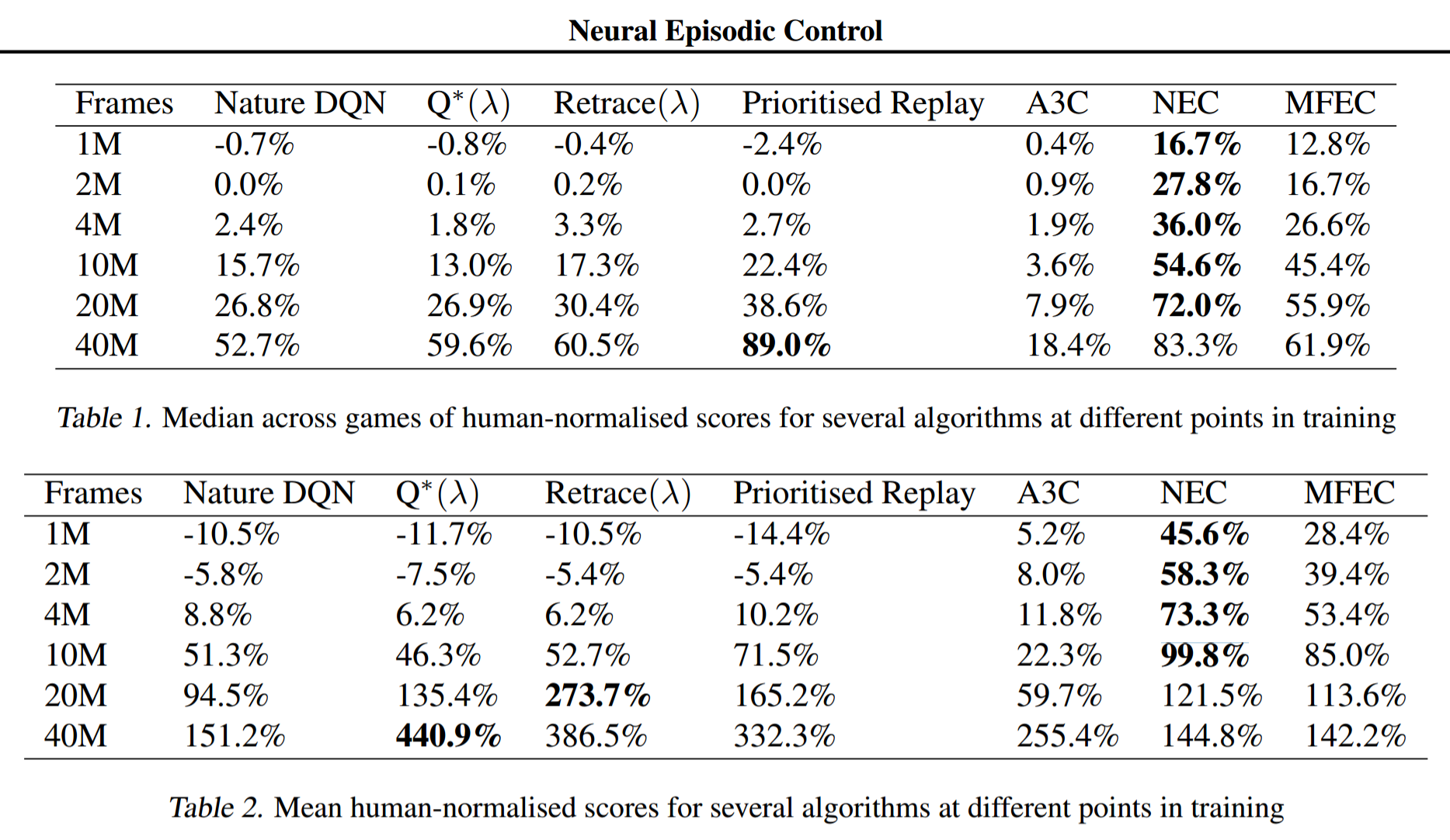
Neural Episodic Control
Experiments
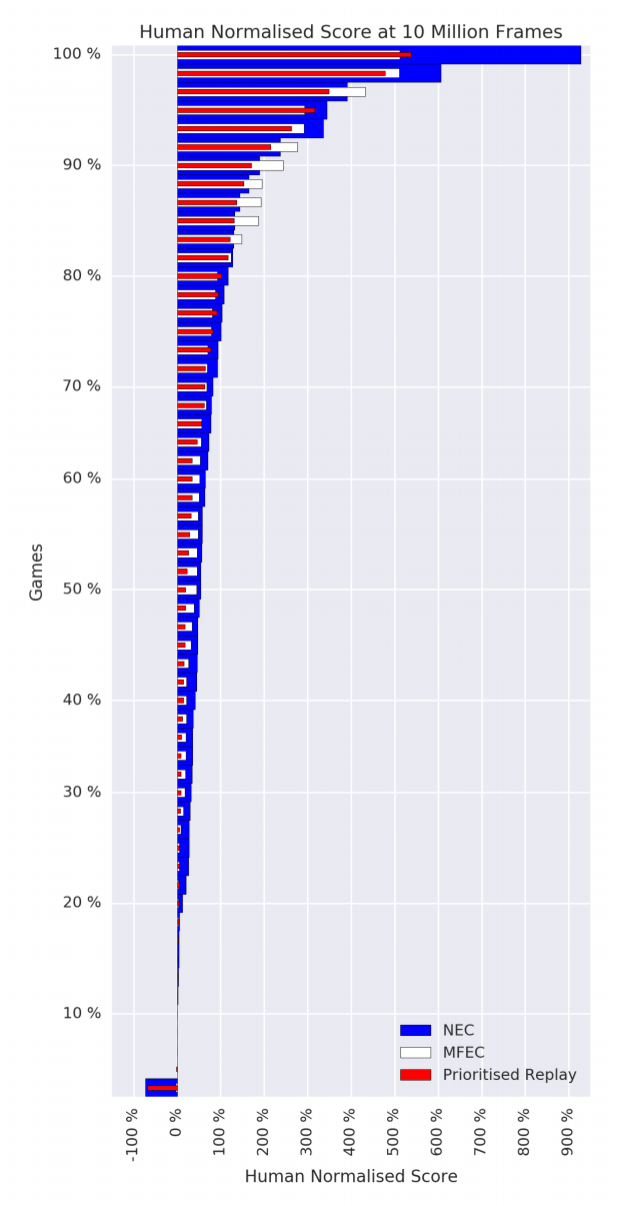
Neural Episodic Control (2016) | DeepMind, 115 citations
Thank you for your attention!
advanced_topics_in_rl_memory
By supergriver
advanced_topics_in_rl_memory
- 2,383



