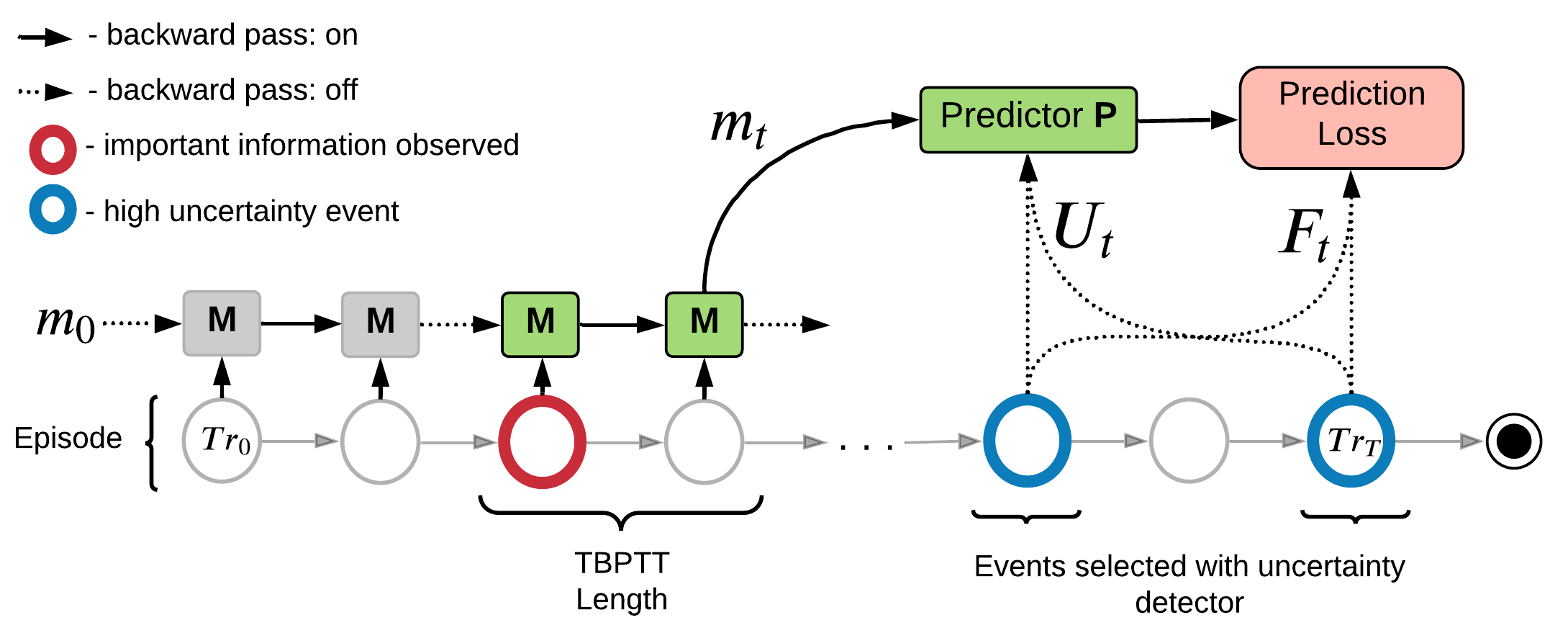
Predicting High Uncertainty Events to Train Working Memory
Artyom Sorokin
18 December 2021
Memory is Important
in many tasks, but we start from Reinforcement Learning...
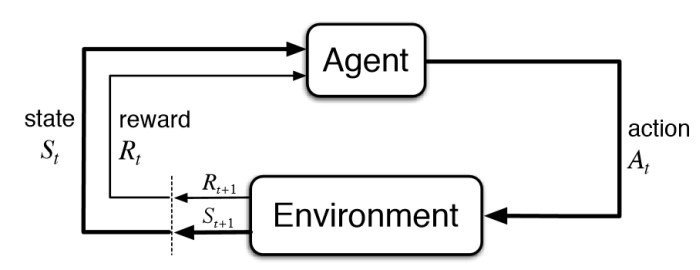
Markov Decision Process
Basic Theoretical Results in Model-Free Reinforcement Learning are proved for Markov Decision Processes.
Markovian propery:
In other words: "The future is independent of the past given the present."
Markov Decision Process
Basic Theoretical Results in Model-Free Reinforcement Learning are proved for Markov Decision Processes.
Markovian propery:
In other words: "The future is independent of the past given the present."

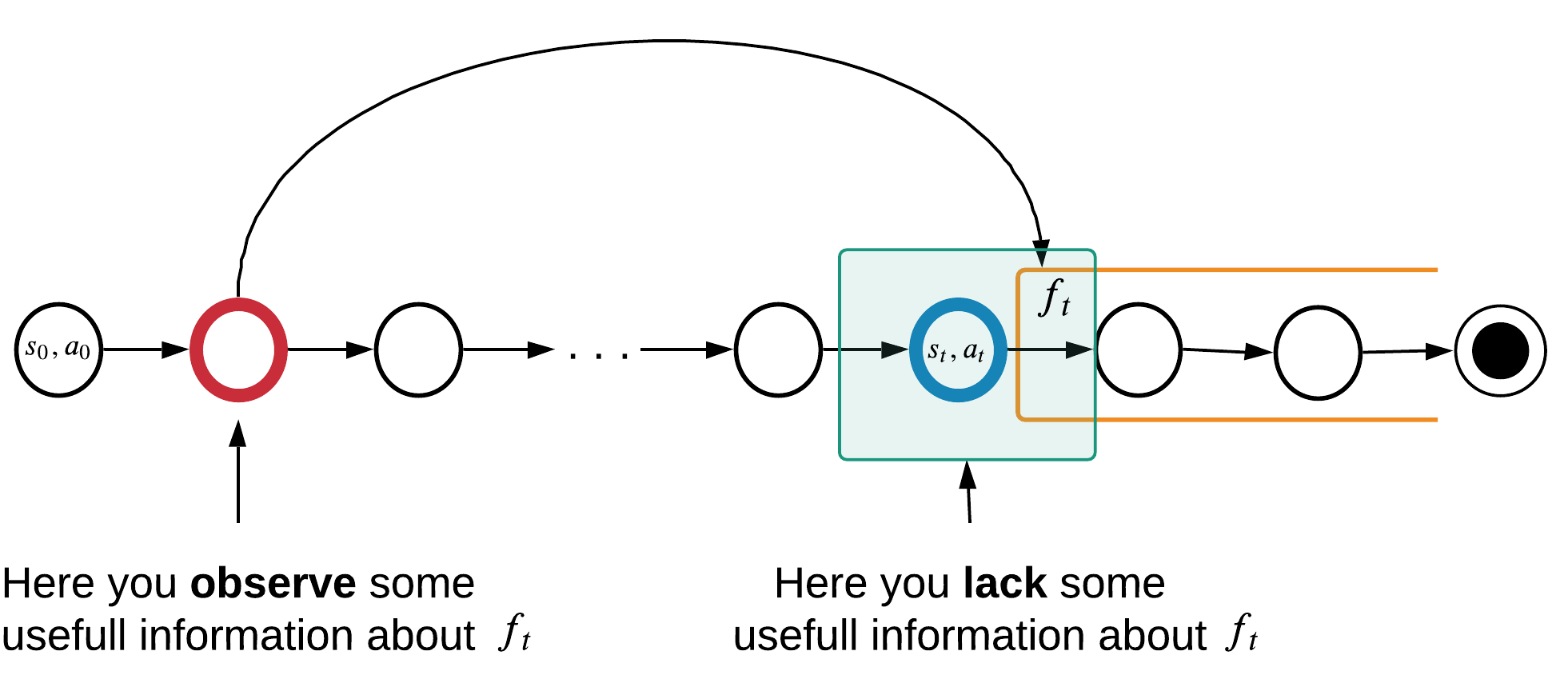
When does agent observe the state?



Memory in RL
Why We Need Working Memory?

\(obs_{t=10}\)

\(obs_{t=12}\)
\(obs_{t=20}\)


\(act_{t=10}\)
\(act_{t=12}\)
\(act_{t=13}\)
We need this information
At this moment!
Memory
. . .
. . .
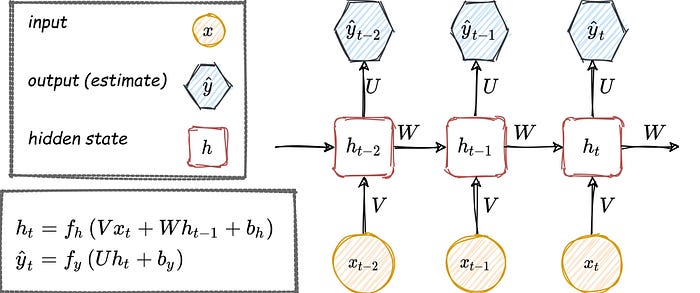
Recurrent Memory:



\(obs_{t=10}\)

\(obs_{t=12}\)
\(obs_{t=20}\)


\(act_{t=10}\)
\(act_{t=12}\)
\(act_{t=20}\)
\(h_{10}\)
. . .
. . .
\(h_9\)
\(h_{19}\)
. . .
. . .
. . .
Information
Gradients
Problem with RNNs:

Solutions for Vanishing Gradients
Fight RNN problems by building more complex RNNs

Long-Short Term Memory: LSTM

Differential Neural Computer: DNC
Window Based Memory



\(obs_{t=10}\)

\(obs_{t=12}\)
\(obs_{t=20}\)


\(act_{t=10}\)
\(act_{t=12}\)
\(act_{t=20}\)
. . .
. . .
Information
Gradients
Memory Window
Transformer is a window-based memory architecture

Soft-Attention:
\(obs_{t=10}\)
\(obs_{t=12}\)
\(obs_{t=20}\)

. . .
. . .



\(e_{10}\)
\(e_{12}\)
\(a_{10}\)
\(e_{20}\)
Embeddings
Query
\(a_{12}\)
Attention weight: \(a_t = {e_{t}}^T q/\sum_i {e_{i}}^T q \)
\(q\)

Soft-Attention:
\(obs_{t=10}\)
\(obs_{t=12}\)
\(obs_{t=20}\)

. . .
. . .



\(e_{10}\)
\(e_{12}\)
\(a_{10}\)
Embeddings
Query
\(a_{12}\)
Context Vector \(c_{20} = \sum_t a_t e_t\)
Attention weight: \(a_t = {e_{t}}^T q/\sum_i {e_{i}}^T q \)
\(q\)

Transformer Basics: Self-Attention
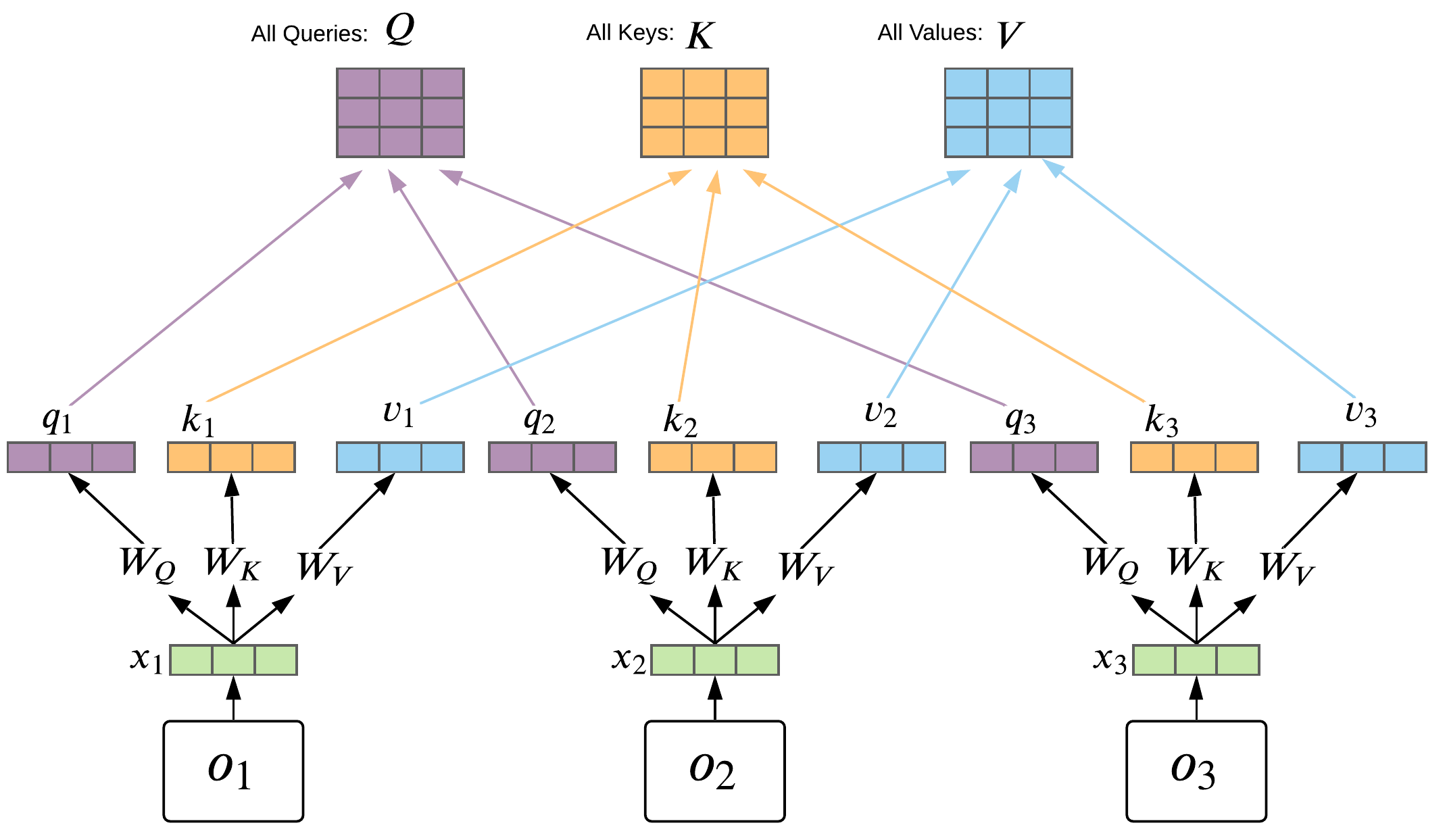



Transformer Basics: Self-Attention
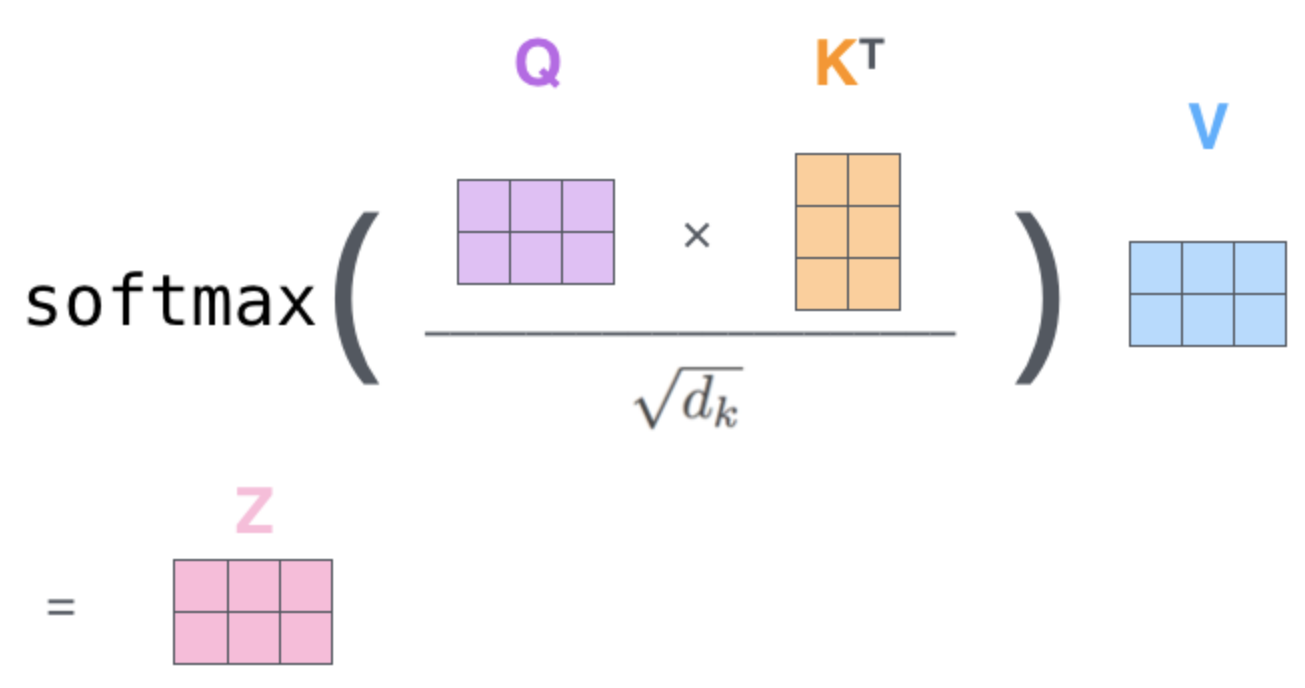
Self-Attention computation:
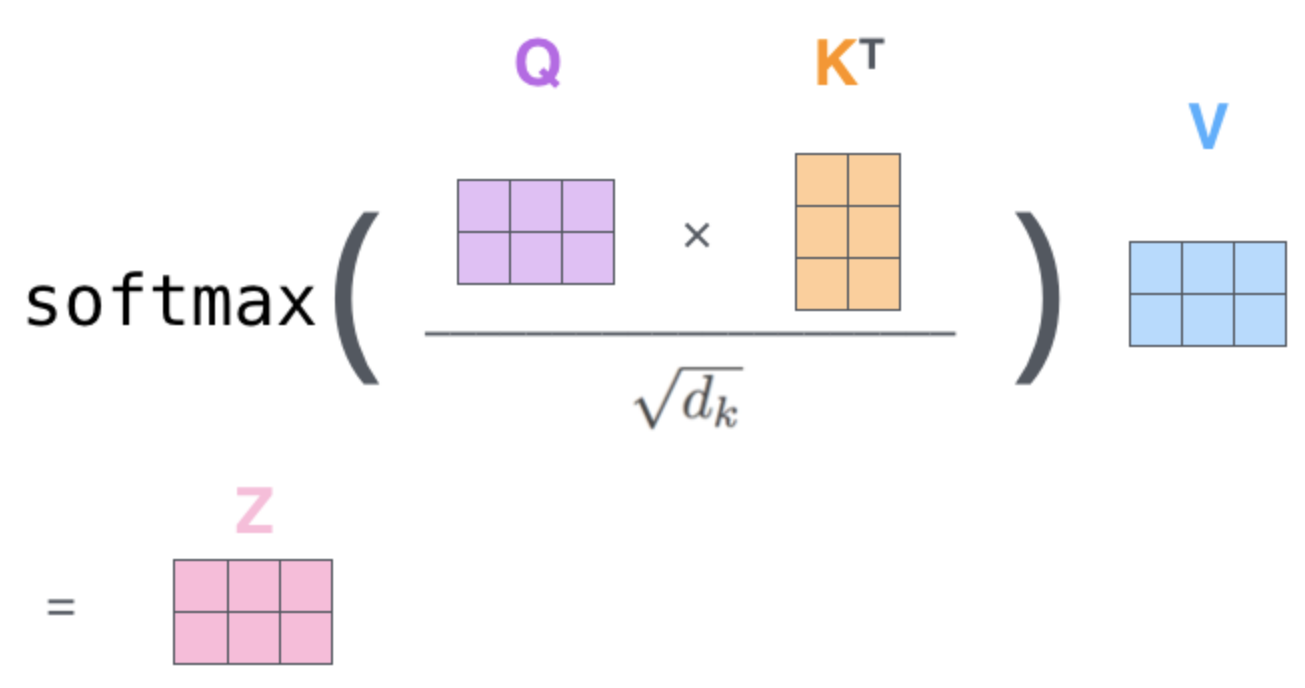
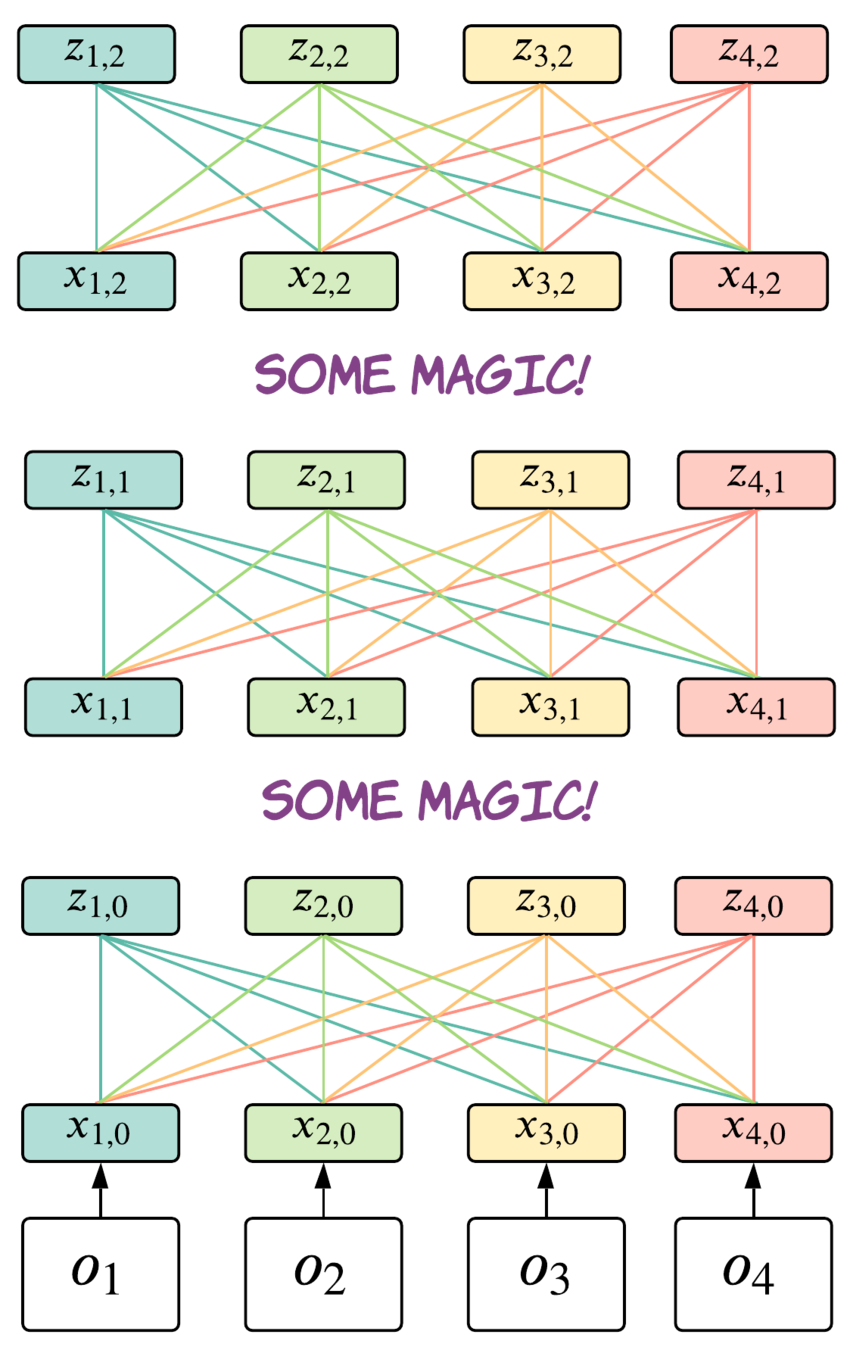
Each \(z_t\) contains relevant information about \(o_t\) collected over all steps in
Memory Window:

Full Transformer

This is how real Transformer looks:
Kind of...
This is how real Transformer looks:
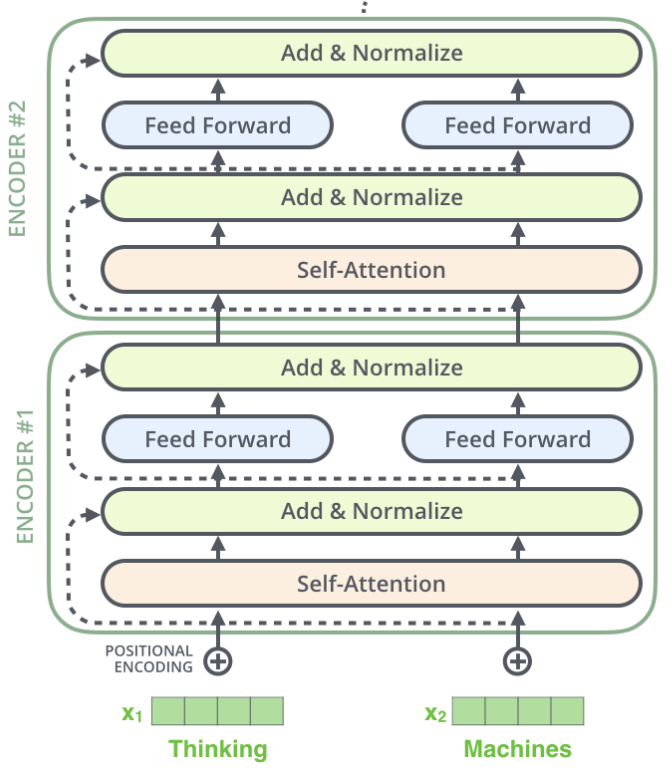

Transformer:
- All time-steps in a memory window attends to all other time-steps
- For each time-step you have: Query \(q_t\), Key \(k_t\), Value \(v_t\)
- Transformer has N attention heads!
- Transformer uses positional encoding to relate different time steps temporarily
- You repeat this process for several layers!
Transformer
Attention is All You Need!


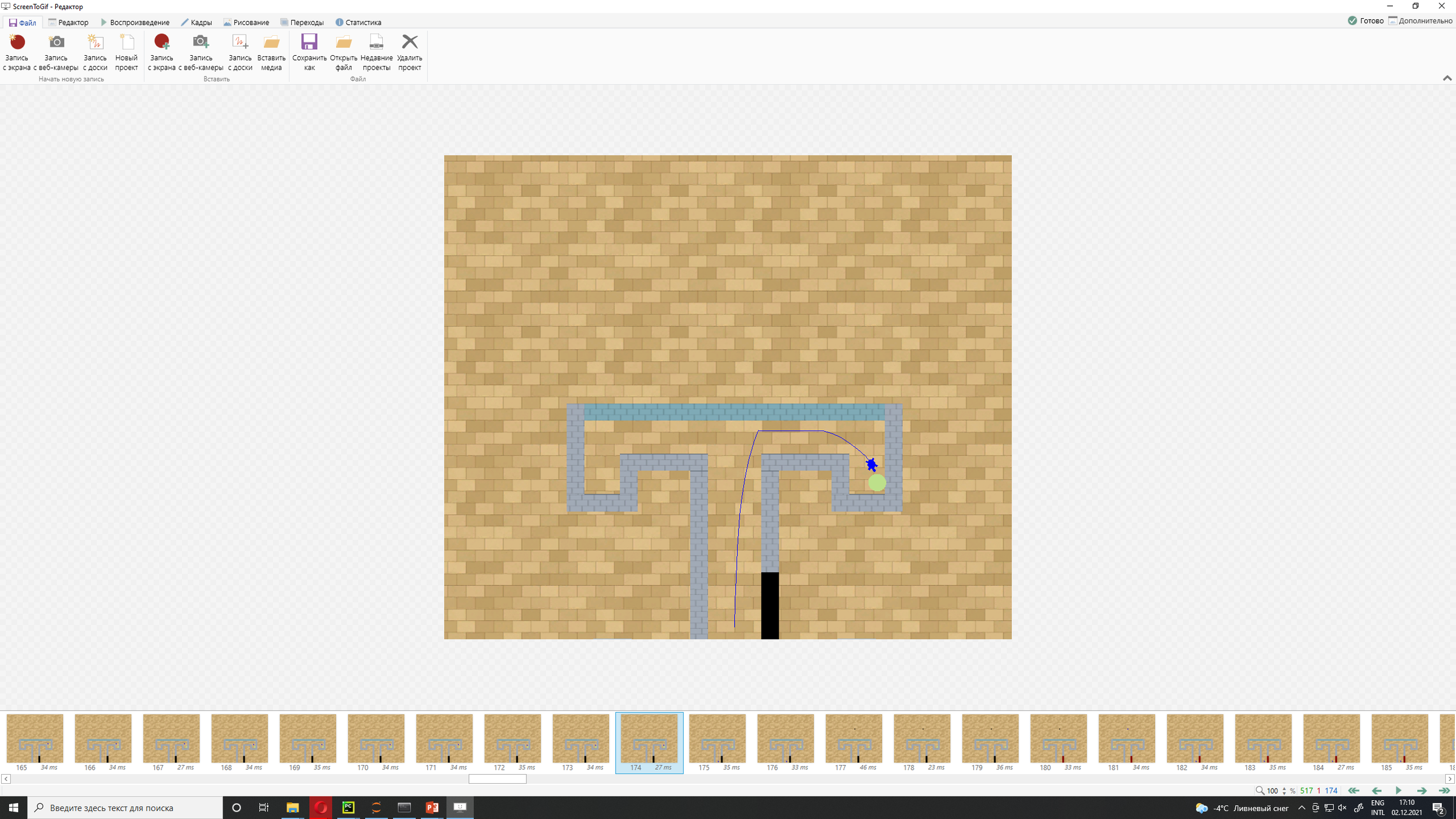
T-Maze Example
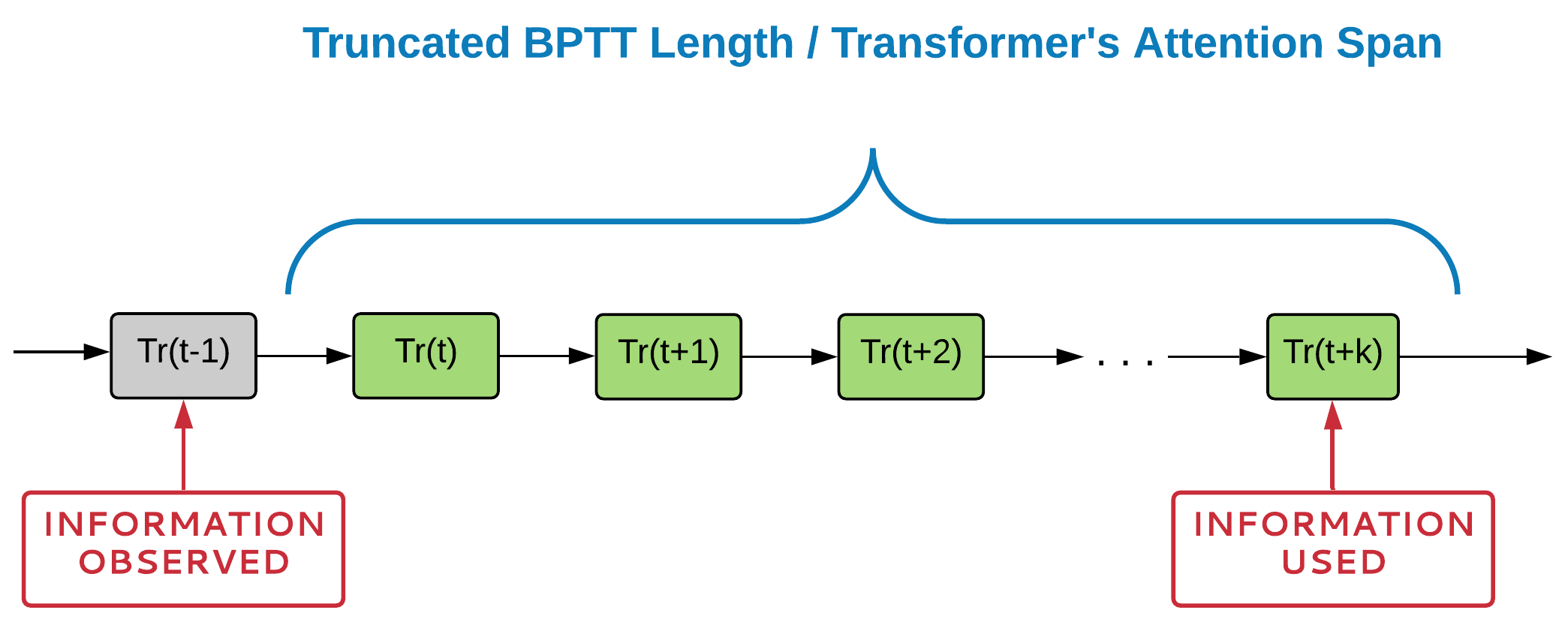
Truncated BPTT gradients
agent panda
RNNs
Information observed
Transformer attention span
agent panda

Information observed
Transformers
Problems with RNN and Transformers
-
Temporal dependency should fully fit into TBPTT or Attention Span to be learned
-
You need to process all intermediate steps to implement backpropagation over Attention Span/TBPTT
Problem with RNN and Transformers

Problem:
We need to backpropagate through all intermediate steps
to find and learn temporal dependency
Temporal dependency should fit into TBPTT/Attention Span to be learned
As we can't detect temporal dependency locally
? ? ? ? ?
What if we could detect temporal dependencies locally?
Temporal dependency between t-1 and t+k
Problems with RNN and Transformers
-
RNN-based solutions:
-
Vanishing/Exploding Gradients
- Hidden State Bottleneck
- Trajectory Noise Sensitivity
- Linear complexity without attention
-
-
Transformers-based solutions:
- Quadratic space and time complexity for most architectures
- Less stable in RL
- Linear space and time complexity for some architectures (which are not equal to full Self-Attention)
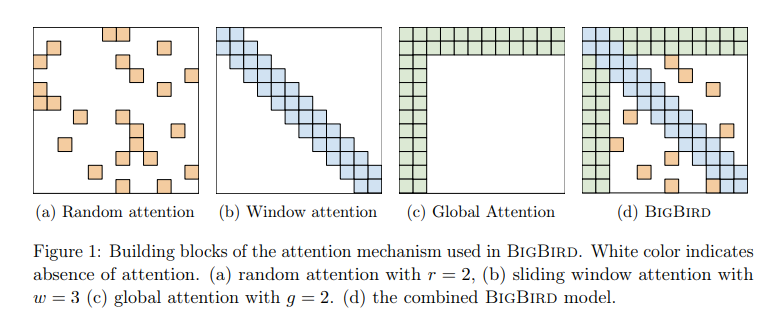

TBPTT and Attention Spans in RL:
-
RNN and MANN:
-
100-250 steps for AMRL
-
40-80 steps for R2D2
-
Best results that i know 500+ steps with MERLIN (Wayne et al, 2018)
-
-
Transformers:
- 512 steps in Stabilized Transformer
- 2048 for GPT3 in Supervised Learning
- 4096 for Linformer and BigBird
Idea: long version
Can we find temporal dependencies locally?
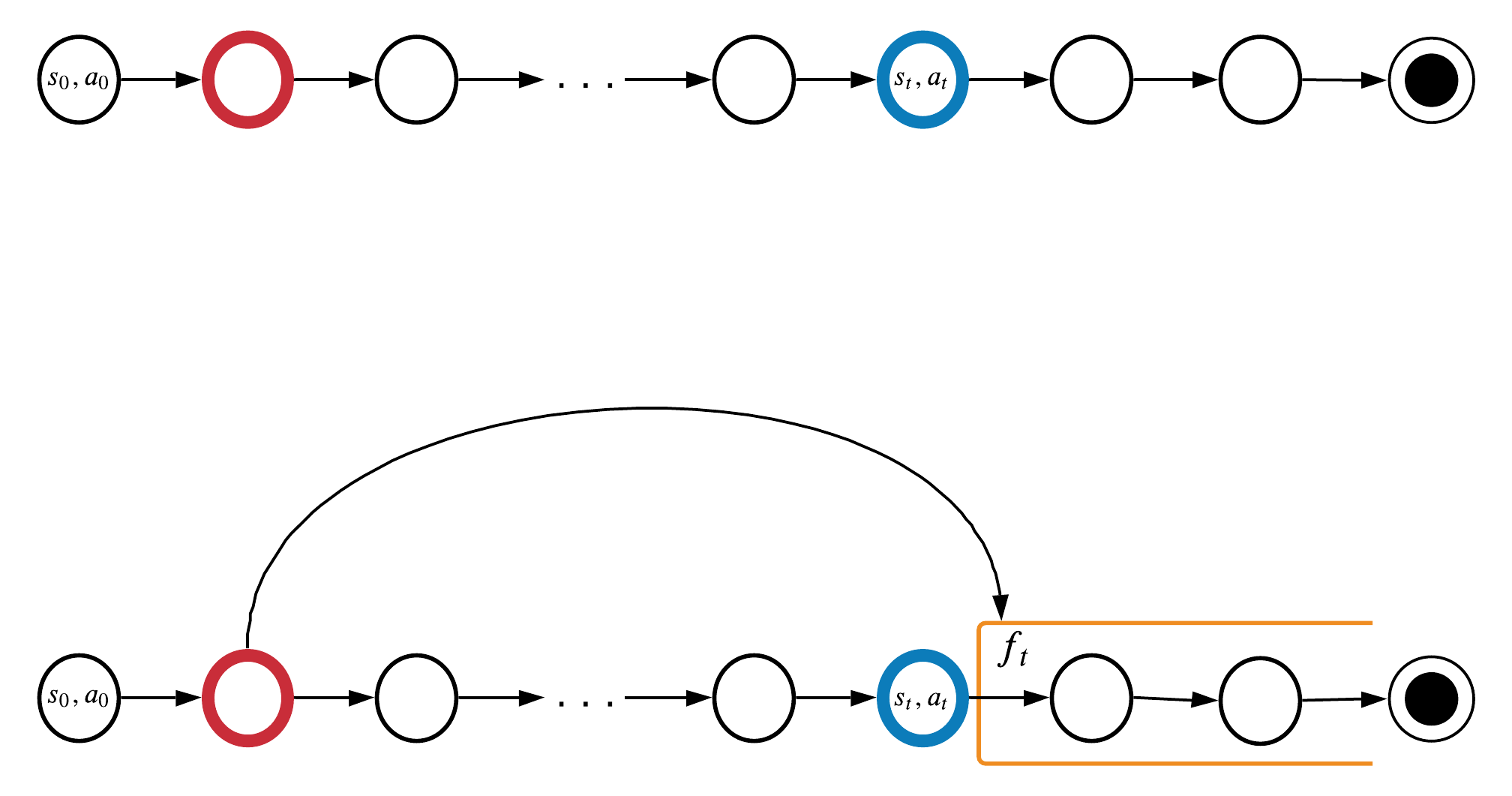
Information from red timestep could help at blue timestep.
Markov property doesn't work for these timesteps:
How important it is to remember the red timestep?

\(y_t\) can be Q-value, \(s_{t+1}\), \(r_{t+1}\), etc.
Can we find temporal dependencies locally?
Information from red timestep could help at blue timestep.
Markov property doesn't work for these timesteps:
How important it is to remember the red timestep?

\(f_t\) can be Q-value, \(s_{t+1}\), \(r_{t+1}\), etc.
multiplied by \(P(o_{t-k}| o_t, a_t)\)
Memory's Objective
The best memory would maximize the following sum:

But training \(m_t\) to maximize Mutual Information (MI) at step \(t\) doesn't help with our problem:
what if at information from step \(t-k\) is already lost at step \(t\)
It is better to optimize the following sum:
Memory's Objective
The best memory would maximize the following sum:

But training \(m_t\) to maximize Mutual Information (MI) at step \(t\) doesn't help with our problem:
what if at information from step \(t-k\) is already lost at step \(t\)
It is better to optimize the following sum:
Memory's Objective
Train memory to maximize MI for all future steps:
\(O(T^2)\) in time!
Idea:
Instead of optimizing the whole second sum it would be cheaper to optimize w.r.t. to the moments where memory is the most important for model's predictions!
still requires to process full sequence to update \(m_t\)
- Not all future events depends on all information from the past
- Not all \(I(f_\textcolor{blue}{i} ; m_\textcolor{black}{t} | o_\textcolor{blue}{i}, a_\textcolor{blue}{i})\) are created equal!
Locality of Reference
Finding Important Moments
how important memory can be in \(f_t\) prediction
If \(H(f_{t}|m_{t}^*, o_{t}, a_{t})\) doesn't fluctuate as much as \(H(f_{t}| o_{t}, a_{t})\), e.g. \(H(f_{t}|m_{t}^*, o_{t}, a_{t}) = c\) for any \(t\)
\(f_t\) uncertainty without memory
\(f_t\) uncertainty with perfect memory
Then \(I(f_{t} ; m_{t}^* | o_{t}, a_{t})\) is proportional to \(H(f_t|o_t, a_t)\)
Goal: Find moments where memory is the most important for model's predictions!
specify how much memory from step \(t\) can improve prediction.
Problem: To find steps were memory is useful we first need to have a useful memory :(
Let's assume we have a perfect memory \(m^{*}_t\)! Then:
Resume
Train memory to maximize MI at moments that would benefit the most from using memory:
where \(U_t\) is a set of steps with the highest ; \(|U| \ll T\)
Before:
After:
Train memory to maximize MI for all future steps:
Idea: short version
memory potential:
how important memory can be in \(f_t\) prediction
If \(H(f_{t}|m_{t}^*, o_{t}, a_{t})\) doesn't fluctuate as much as \(H(f_{t}| o_{t}, a_{t})\), e.g. \(H(f_{t}|m_{t}^*, o_{t}, a_{t}) = c\) for any \(t\)
\(f_t\) uncertainty without memory
\(f_t\) uncertainty with a perfect memory
Then \(I(f_{t} ; m_{t}^* | o_{t}, a_{t})\) is proportional to \(H(f_t|o_t, a_t)\)
Imagine we have a perfect memory state \(m^*_t\) for each t!
Local Metric: Conditional mutual Information
Can we find temporal dependencies locally?
detects the end of a temporal dependency
find ends of temporal dependencies by estimating this
memory potential:
how important memory can be in \(f_t\) prediction
If \(H(f_{t}|m_{t}^*, o_{t}, a_{t})\) doesn't fluctuate as much as \(H(f_{t}| o_{t}, a_{t})\), e.g. \(H(f_{t}|m_{t}^*, o_{t}, a_{t}) = c\) for any \(t\)
\(f_t\) uncertainty without memory
\(f_t\) uncertainty with a perfect memory
Then \(I(f_{t} ; m_{t}^* | o_{t}, a_{t})\) is proportional to \(H(f_t|o_t, a_t)\)
Imagine we have a perfect memory state \(m^*_t\) for each t!
Local Metric: Conditional mutual Information
Can we find temporal dependencies locally?
detects the end of a temporal dependency
find ends of temporal dependencies by estimating this
Memory's Objective
Train memory to maximize MI at moments that would benefit the most from using memory:
where \(U_t\) is a set of steps with the highest
Given lower bound from Barber, Agakov (2004) you can show that training
with Cross-Entropy Loss is enough to Maximize MI
simply learn to predict \(f_k\) from \(U_t\) steps
Long-Term memory objective
Train memory to maximize MI at moments that would benefit the most from using memory:
where \(U_t\) is a set of steps with the highest
Given lower bound from Barber, Agakov (2004) you can show that training
with Cross-Entropy Loss is enough to Maximize MI
simply learn to predict \(f_k\) from \(U_t\) steps
Intuition
T-Maze Example

hint: stores information about reward placement
reward
- black wall: reward is on the right
- red wall: reward is on the left
agent panda
Intuition
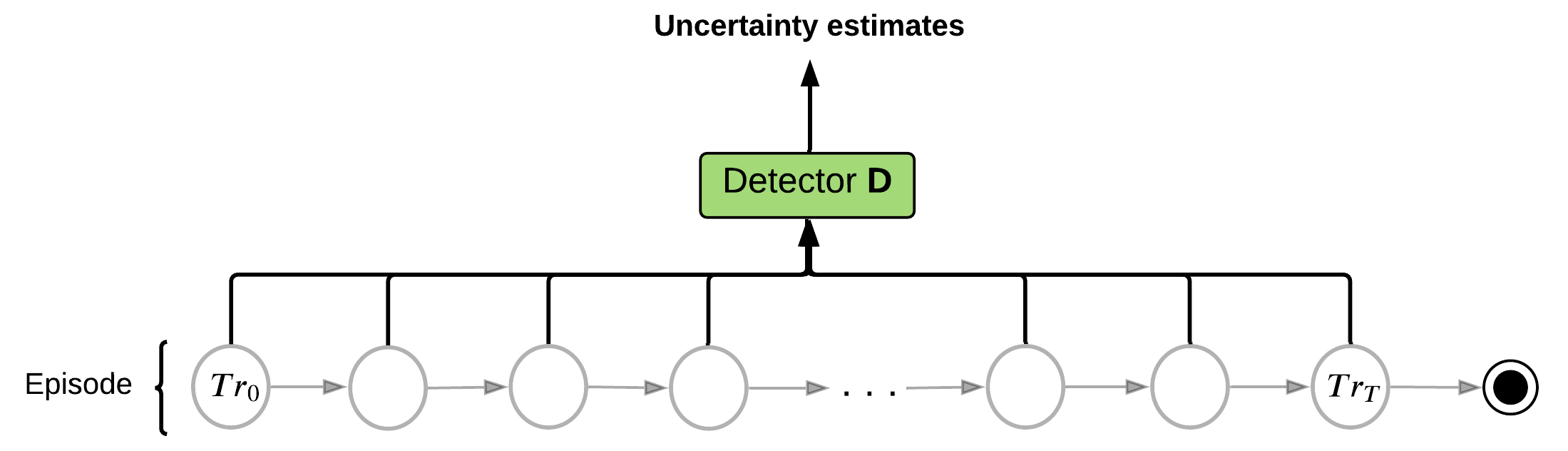
Learning Algorithm:
- Estimate Uncertainty for each step in a trajectory
- Select K steps with highest uncertainty
- Traverse trajectory with memory
- Train memory to predict future at selected high uncertainty steps

high uncertainty estimate
Uncertainty
detector
Memory
Predictor net
Intuition:
Two main steps:
- First we find the most surprising/uncertain events in a sequence
- Then we search sequence for information that explains these events and store it in memory

this means high uncertainty: \(H(f_i|o_i,a_i)\)
Implementation
Practical Implementation for RNN
Memory Pretraining Modules:
- Uncertainty Detector D - Estimates uncertainty \(H(f_i|o_i, a_i)\)
- Memory Module M - learns to store important information
- Predictor P - used to minimize \(H(f_i| m_t, o_i, a_i)\)/ maximize MI
Learning is divided in two phases:
- Memory Pretraining Phase - we train memory without improving agent's policy
- Policy Learning Phase - We train PPO agent, that receives output of the pretrained memory as an additional input.
We use cumulative discounted future reward as prediction target: \(f_t = \sum_k \gamma^k r_{t+k}\)
Practical Implementation for RNN
- Get estimates of local uncertainty for each time step in the episode
Practical Implementation for RNN
- Get estimates of local uncertainty for each time step in the episode
- Select top K moments in episode with highest uncertainty

Practical Implementation for RNN
- Get estimates of local uncertainty for each time step in the episode
- Select top K moments in episode with highest uncertainty
- Pass through the episode and train a memory model to store information that improves predictions at the selected moments
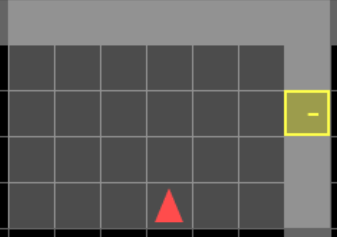
Uncertainty Detection Example:
Environment: Gym-Minigrid (Chevalier-Boisvert et al, 2018)
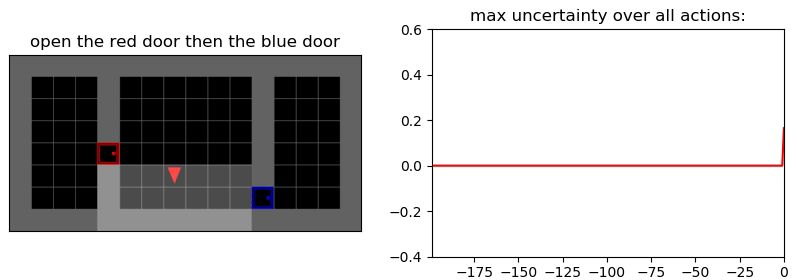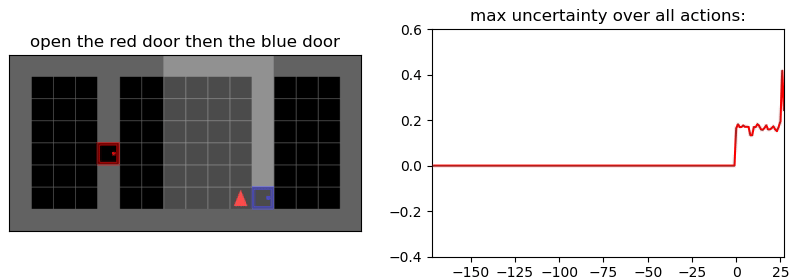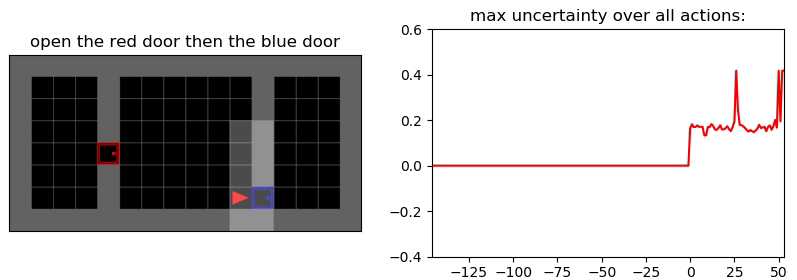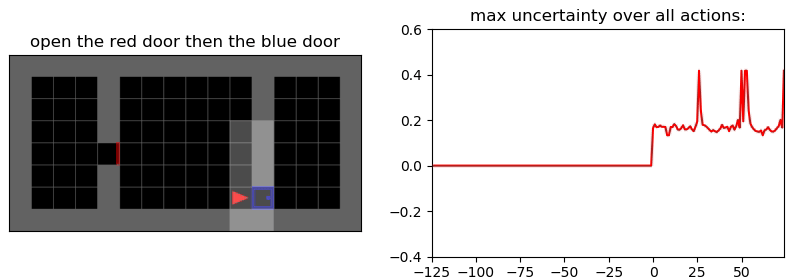
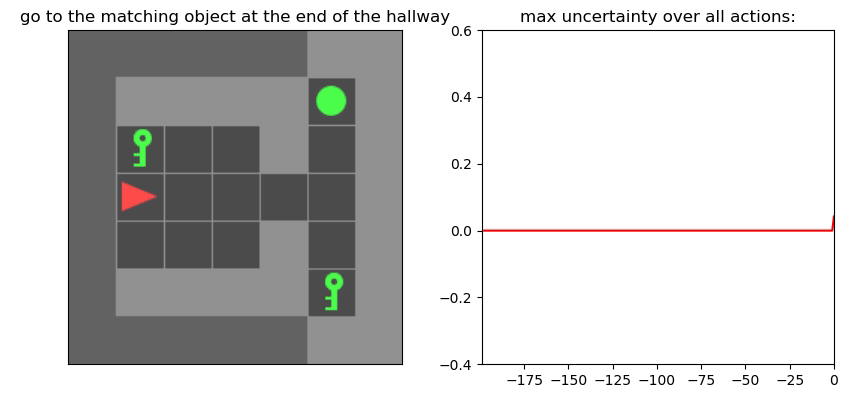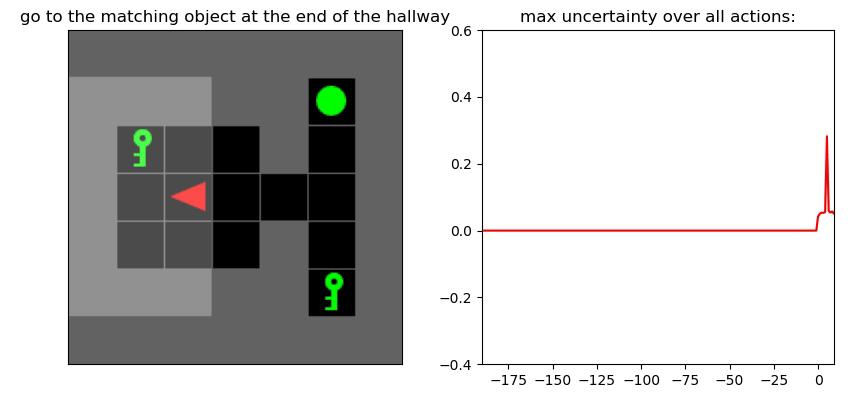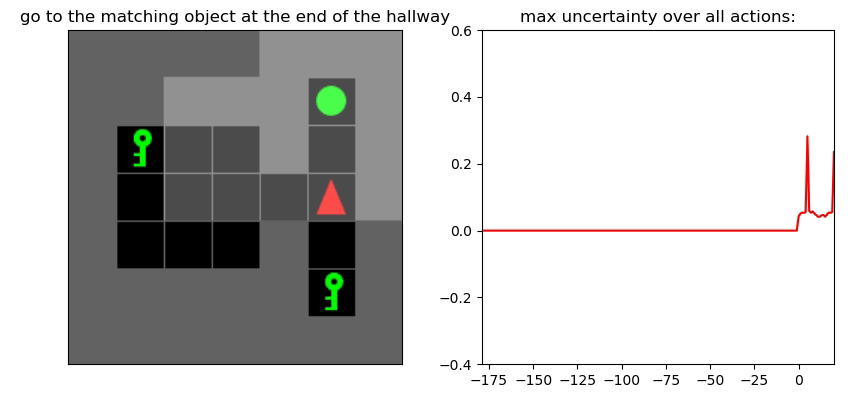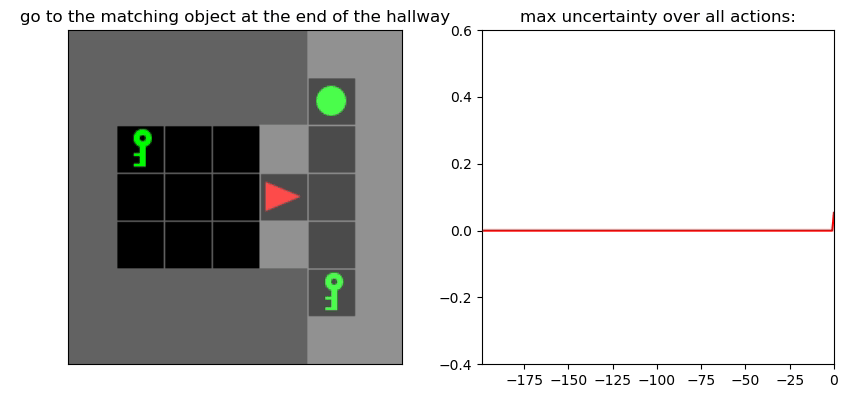
Experiments
Experiments
Baselines
We compare MemUP (Memory via Uncertainty Prediction) with the following baselines:
- PPO-LSTM is a recurrent version of PPO with a single LSTM-layer.
- IMPALA-ST is an IMPALA agent with Transformer-based architecture. The Stabilized Transformer architecture was presented by Parisotto et al. (2020)
-
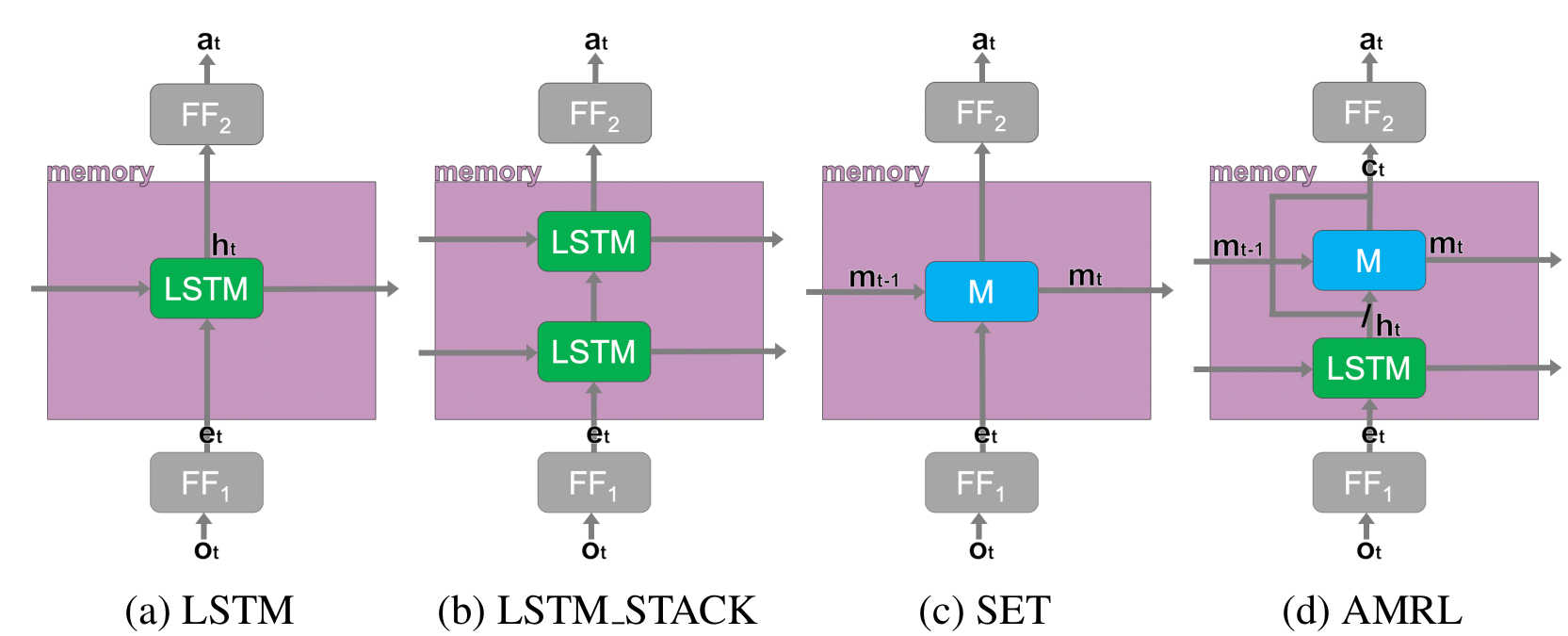
AMRL is proposed by Beck et al. (2020) for the Noisy T-Maze Task. AMRL
is similar to PPO-LSTM baseline, but extends LSTM with AMRL Layer.

IMPALA-ST
Experiments: Noisy T-Maze
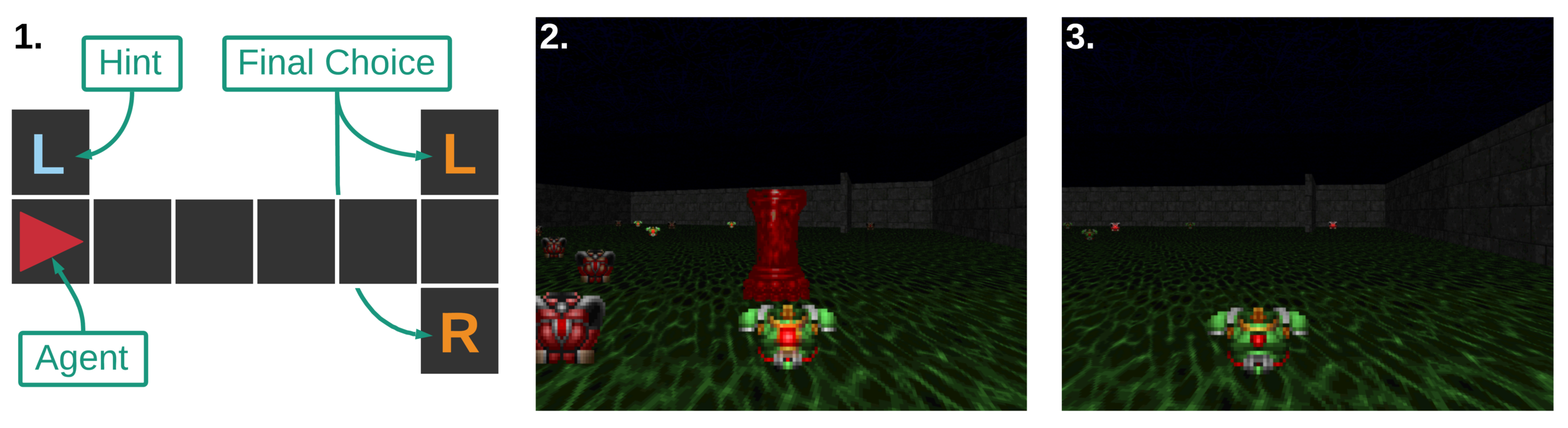
Noisy T-Maze Environment:
- Hard Task in terms of Memory
- Simple Task in every other aspect
Env Details:
- This version was proposed in AMRL paper
- Noisy Observations
- Determine the long-term dependency between hint at the start and reward at the end
- Learn to remember the hint, to achieve maximum reward:
- +4 for matching the hint, -3 otherwise
Experiments: Noisy T-Maze
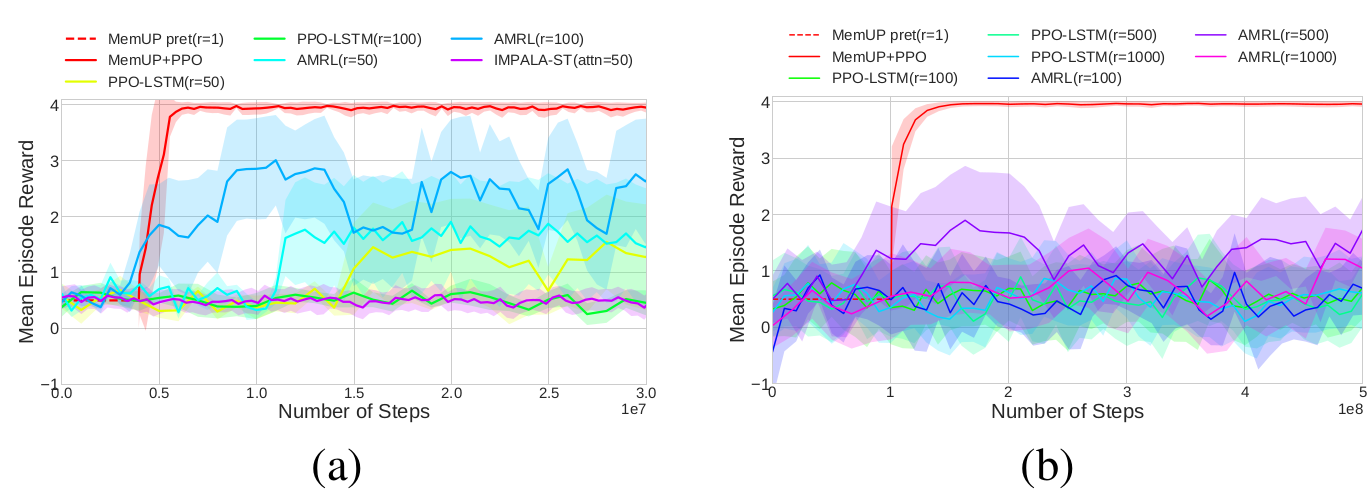
Noisy T-Maze-100
Noisy T-Maze-1000
- All algorithms process sequences shorter than the temporal dependency
- Only MemUp solves the problem consistently
Experiments: Vizdoom

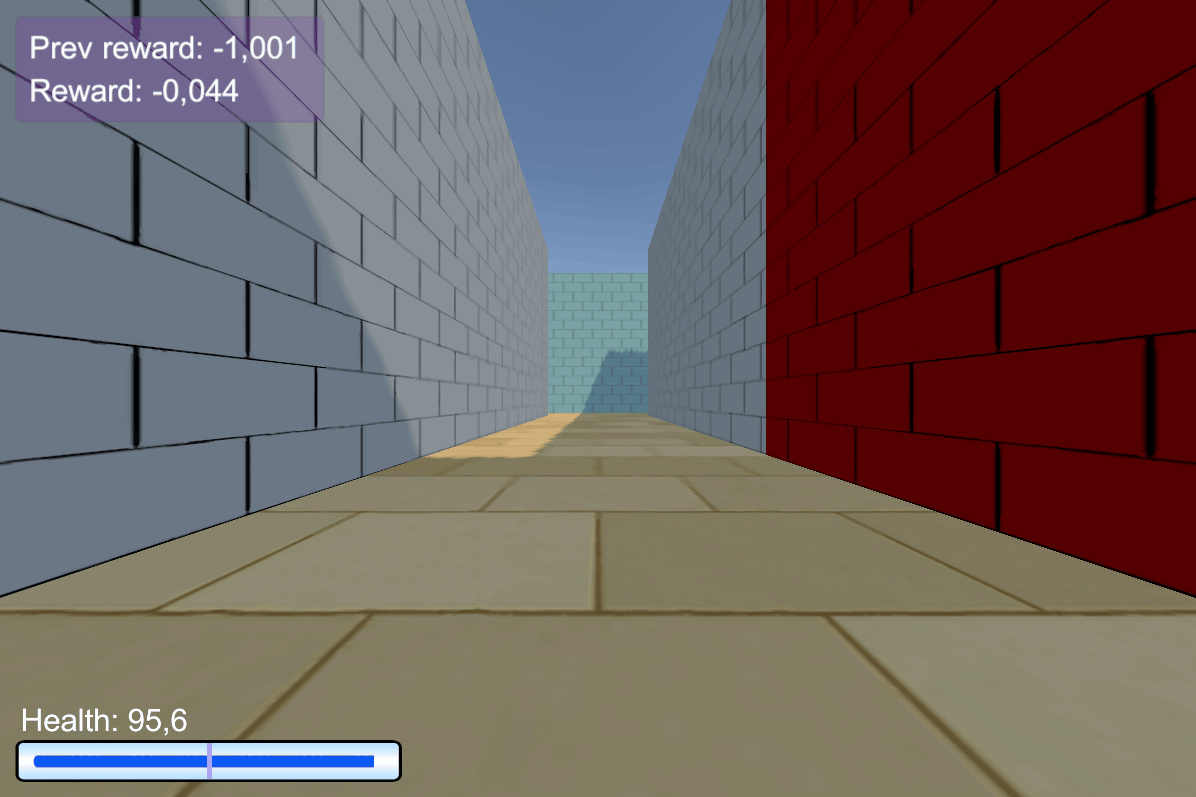
Details:
- Agent walks on acid (-4 health)
- +25 health for objects with a right color, otherwise -25 health
- The column hints the right color of objects
- The column disappears after 45 steps
- +1 reward for the right color, -1 otherwise

ViZDoom-two-colors:
- 3D environment
- Complex observation space
- ~100 steps long temporal dependency
- Proposed in Breeching et al (2019)
Experiments: Vizdoom
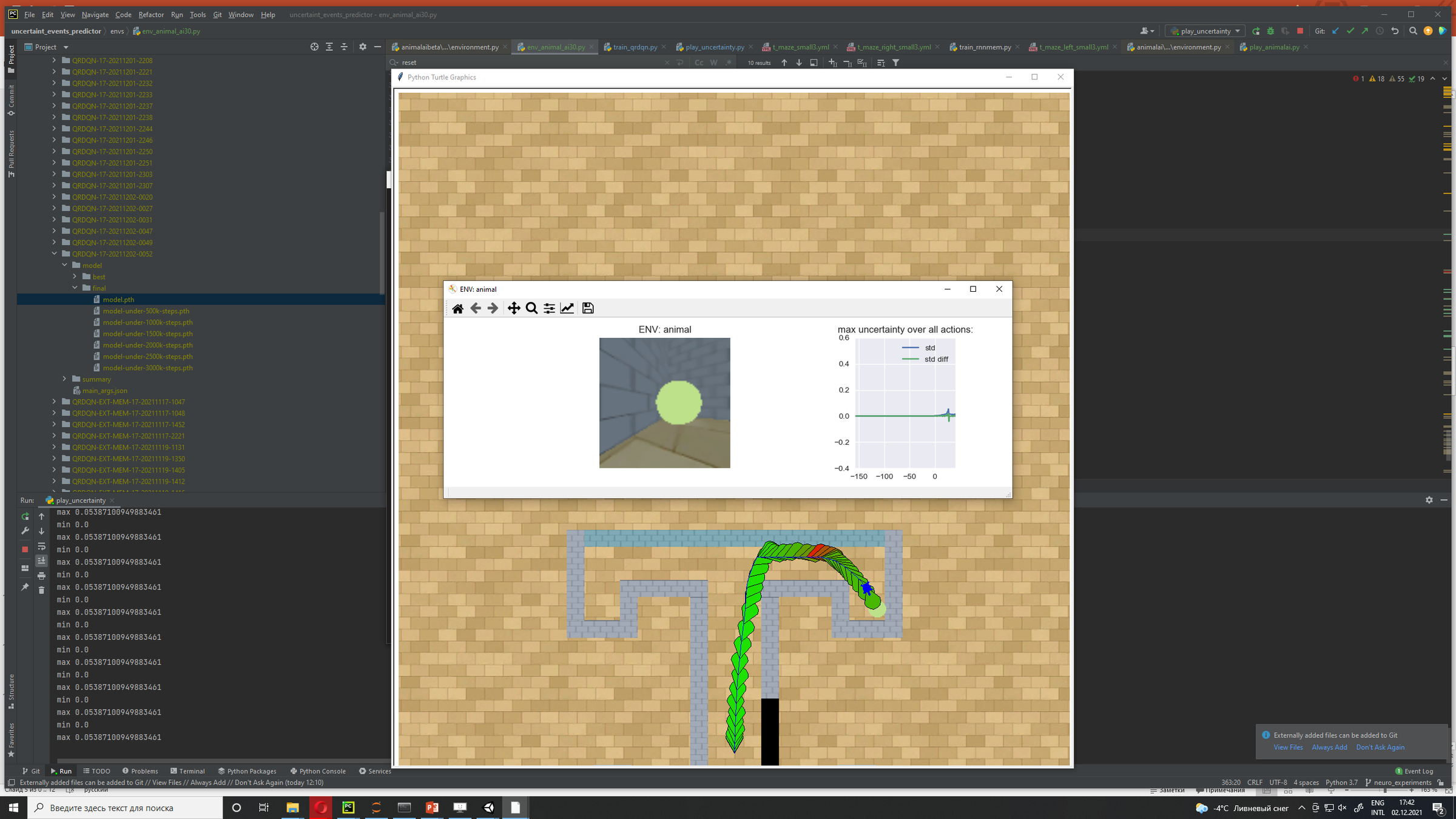
Uncertainty Detector Demonstration
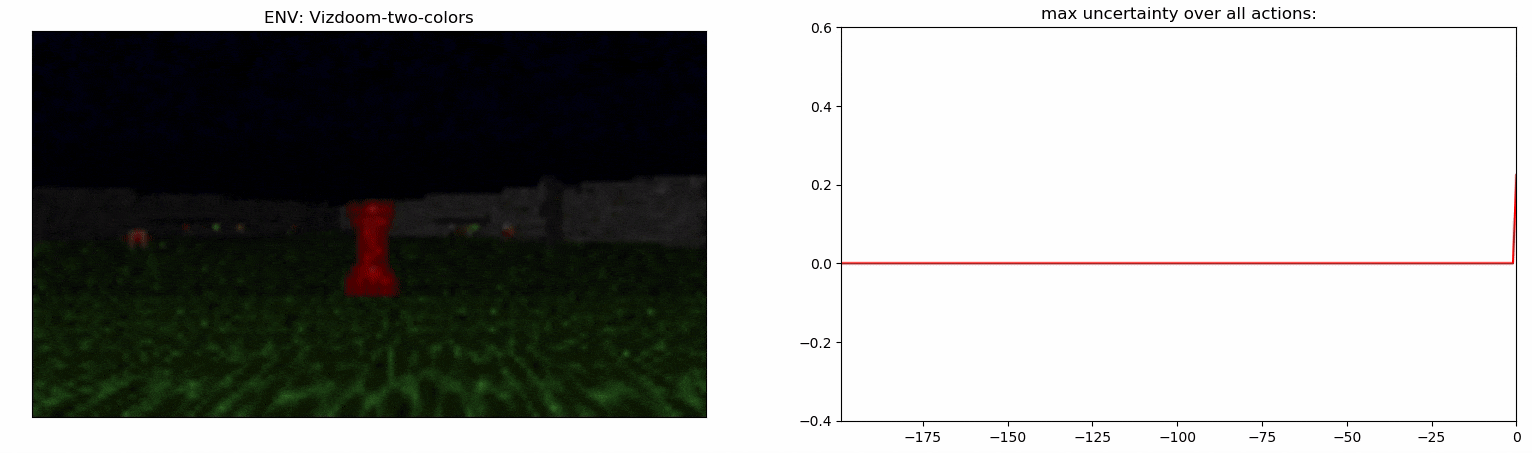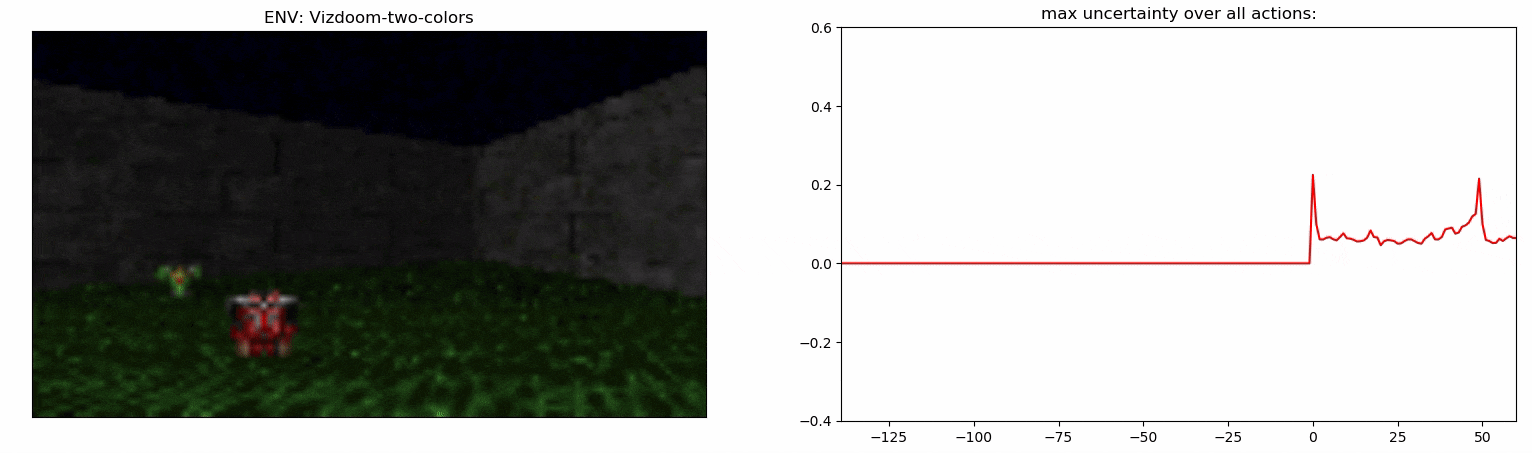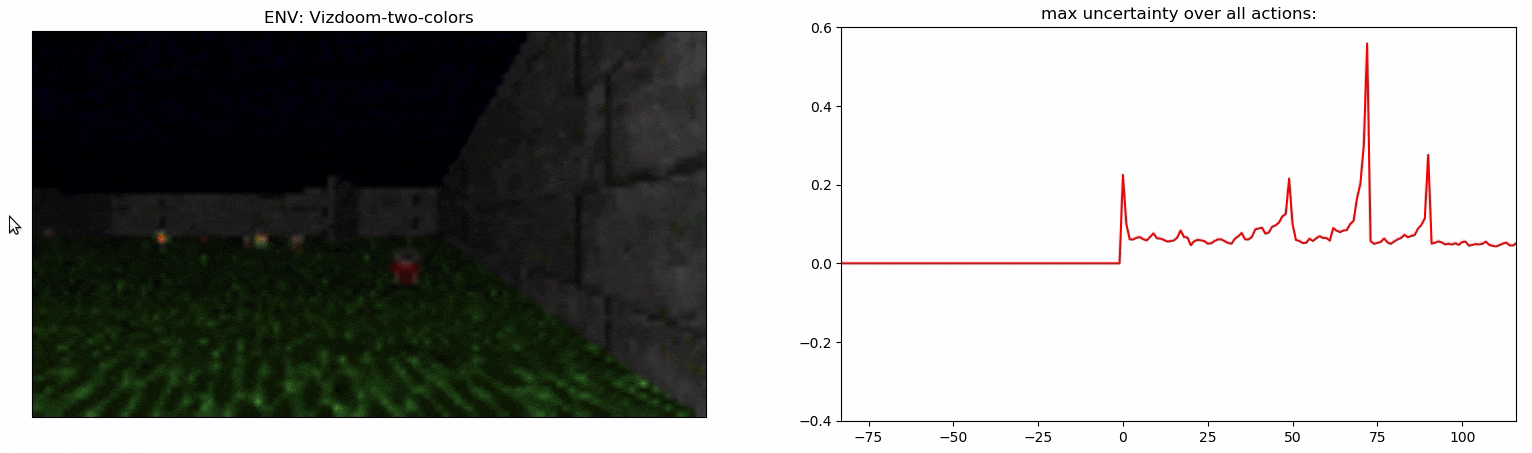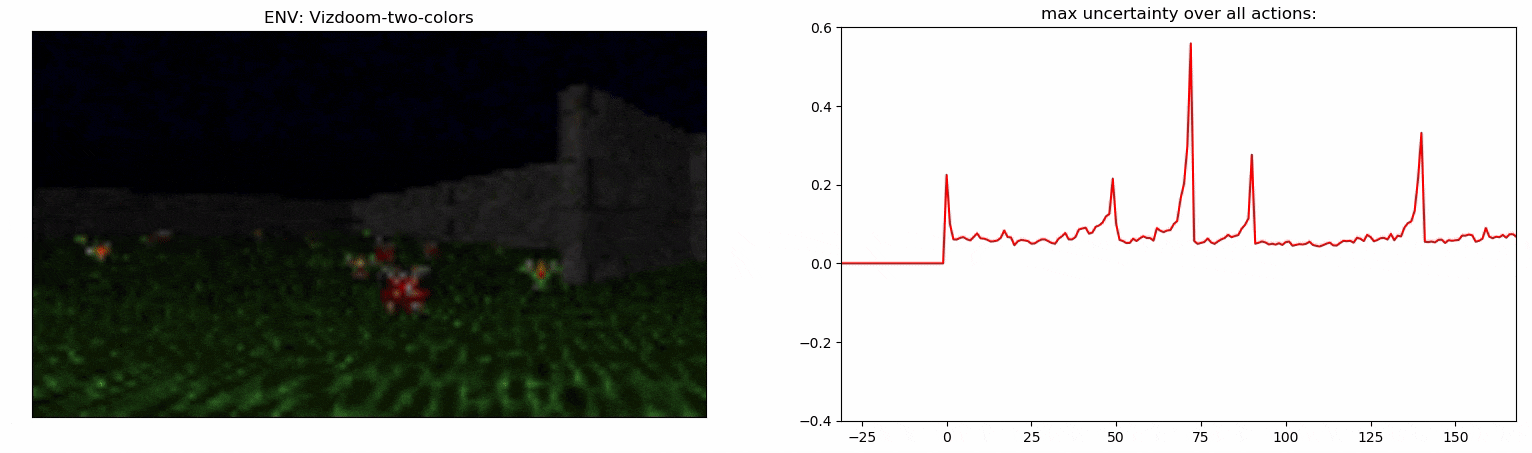
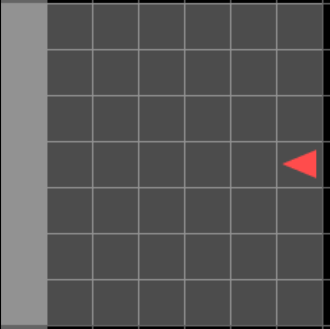
Experiments: Vizdoom
Results
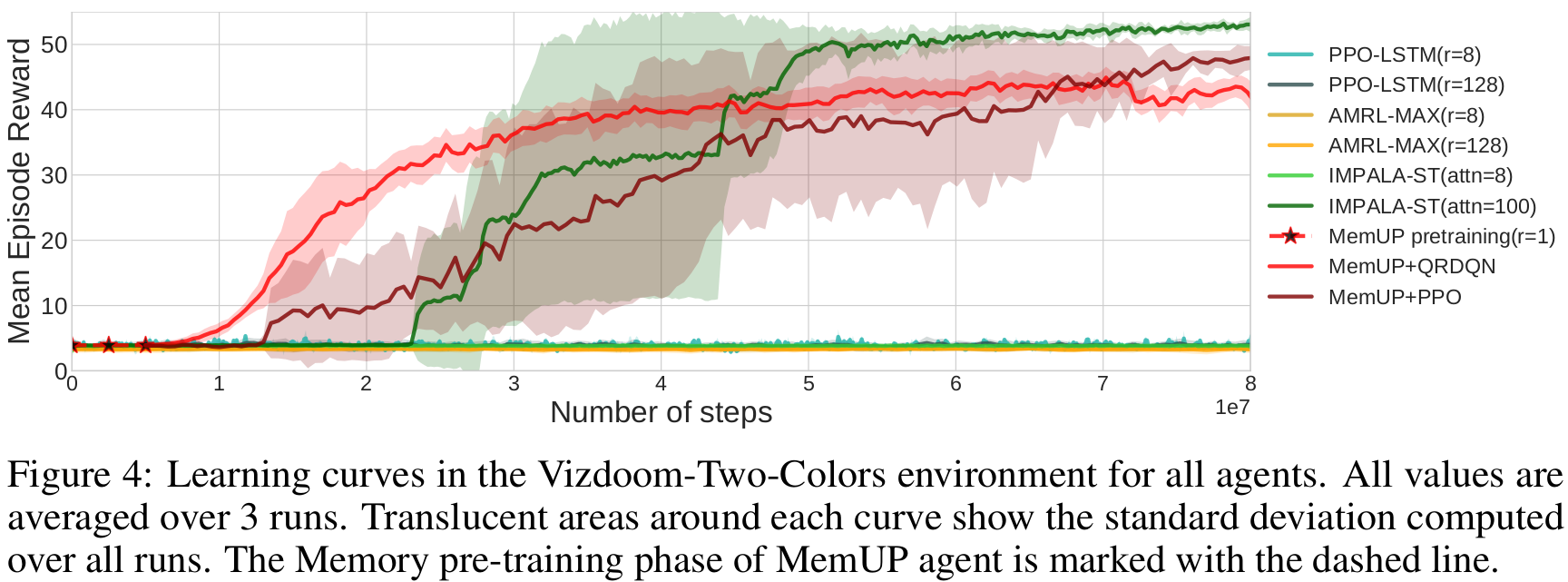
- MemUP solves Vizdoom-Two-Colors
Experiments: Vizdoom
Memory Demonstration

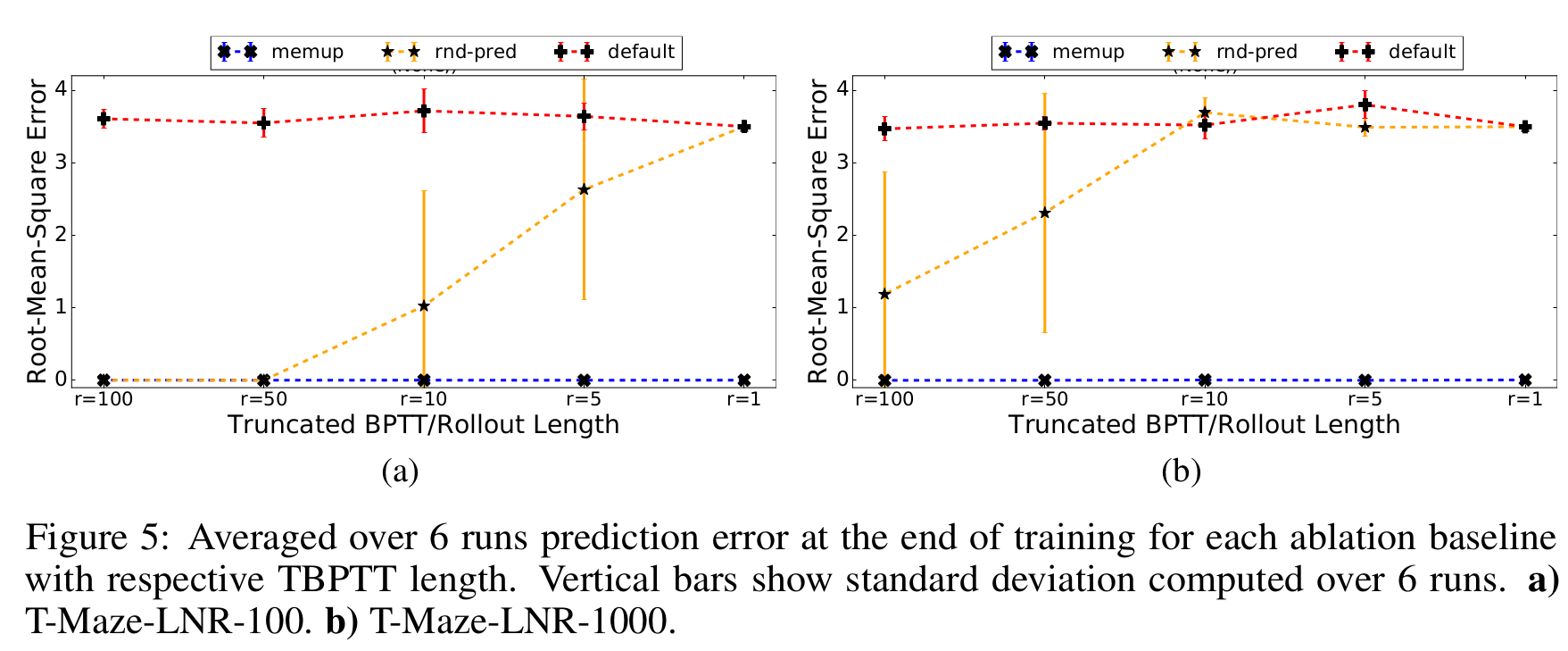
Experiments: Ablation
Ablation Baselines
Memory Baselines:
- MemUP - our proposed algorithm
- Rnd-Pred - Same as MemUP, but events for prediction are selected randomly and uniformly among all future timesteps.
- Default - Same as MemUP, but it is trained to predict return R t at each step t, as oposed to an arbitrarily distant future events as in MemUP and Rnd-Pred.
Experiment Setup:
- Noisy T-maze environment, but we ignore policy learning phase
- Baselines are compared in terms of their ability to predict \(f_t\)
- Separate test set of 100 episodes
Experiments: Ablation
Results
Thank you for your attention!
Request: Comparison with the Papers
- Go-Explore (https://arxiv.org/abs/1901.10995)
- Neural Turing Machines (https://arxiv.org/abs/1410.5401)
- Recurrent Independent Mechanisms (https://arxiv.org/abs/1909.10893)
- PlaNet (https://arxiv.org/abs/1811.04551)
- Big Bird (https://arxiv.org/abs/2007.14062)??
Go-Explore
Detachment
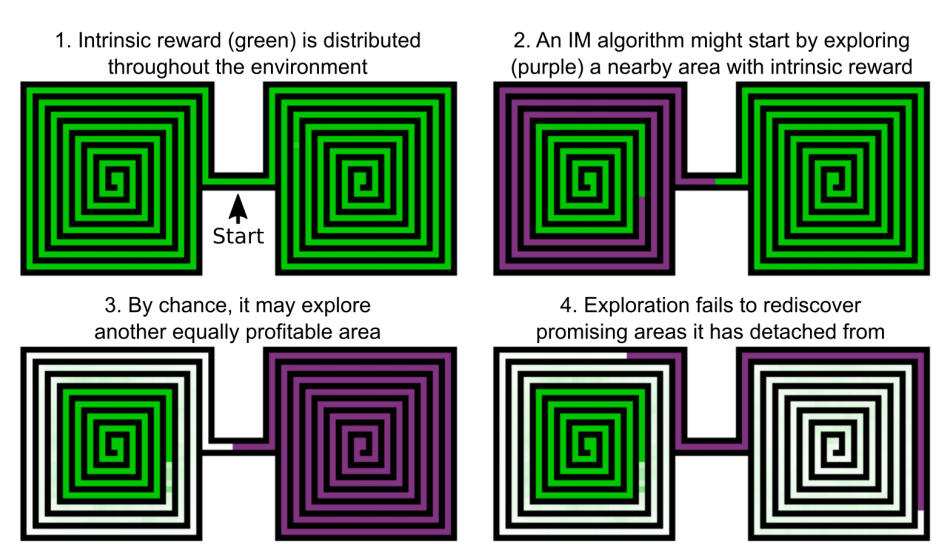
Derailment
Go-Explore improves exploration in environments with sparse rewards
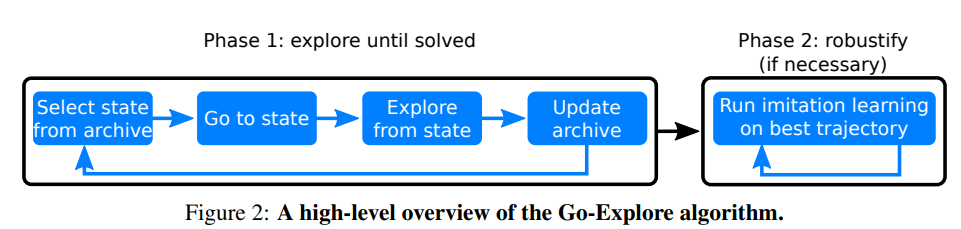
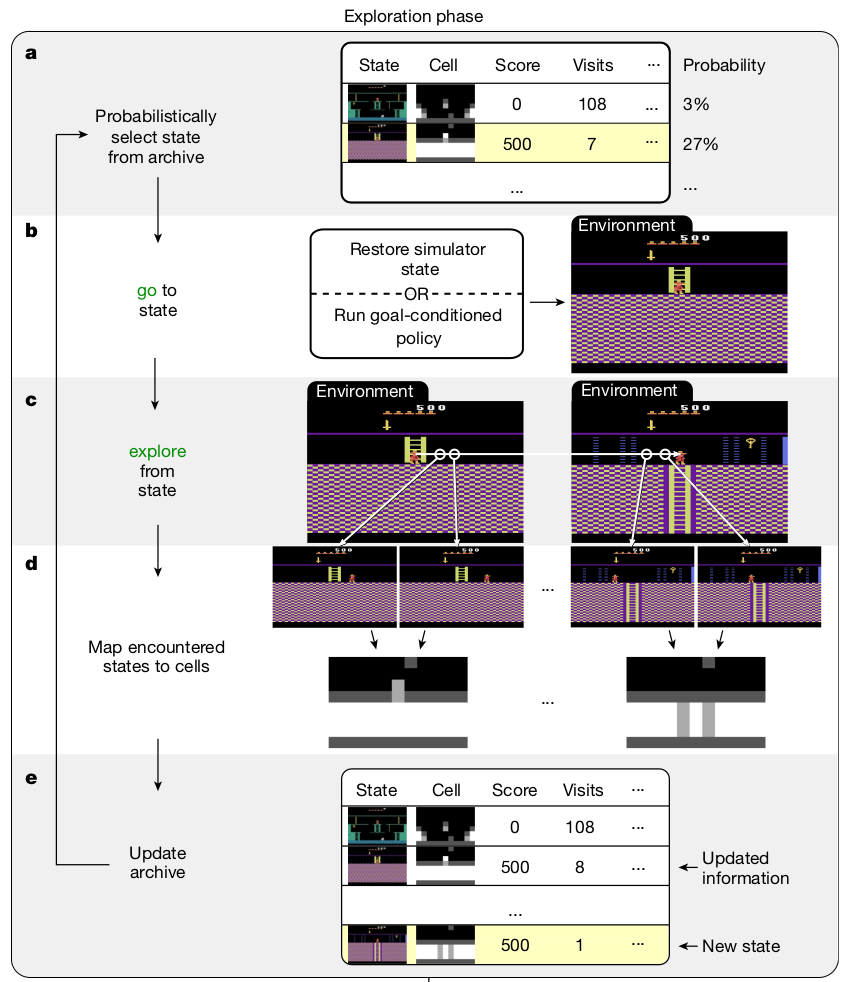
Selection depends on:
#visits, #selections, room_id, level, etc
load from the state/
replay trajectory
random policy
new state or better trajectory
Go-Explore vs MemUP
Similarities:
- Both select some "interesting" states and do something with them :)
Differences:
Go-Explore:
- Goal: Exploration-Exploitation dilemma
- "Interesting" state criterion: Number of Visits / Total Reward
- Interesting states utilization: Explore from them
MemUP:
- Goal: Learning working memory
- "Interesting" state criterion: Lack of information
- Interesting states utilization: Find information about them
NTMs and RIMs
Recurrent neural networks:

Training RNN on Sequences:

LSTM
LSTM
LSTM
LSTM
LSTM
NTMs and RIMs
Neural Turing Machines:
Training NTM on Sequences:


Array of N memory vectors
Read and Write with Soft Attention
NTM
NTM
NTM
NTM
NTM
NTMs and RIMs
Recurrent Independent Mechanisms:
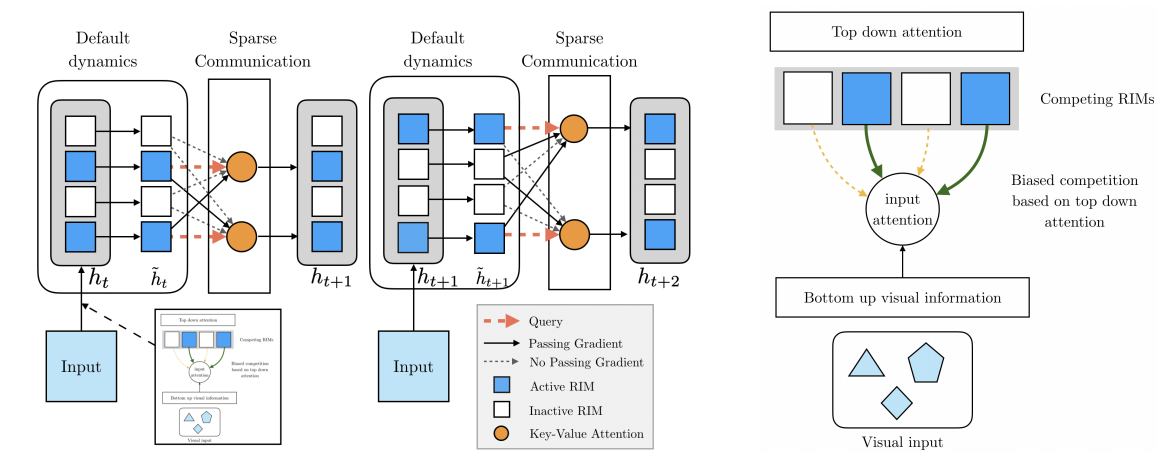
Imagine 4 LSTMS
Choose active LSTMs with
Top Down Attention
Update Active LSTMS
Copy Inactive LSTMS
Training RIM on Sequences:

RIM
RIM
RIM
RIM
RIM
NTMs and RIMs vs MemUP
Similarities:
- Same Goal: Learn and use memory on sequential tasks
Differences:
NTM and RIM:
- Modify architecture
- Main Idea: Keep memory unaltered to fight with Vanishing Gradients
- Temporal dependency should fit in BPTT
MemUP:
- Modifies training procedure
- Main Idea: Predict long-term future selected by the lack of information
- No need to fit temporal dependency in BPTT
We can use NTM, RIM, etc. as a memory module in MemUP
PlaNet
PlaNet builds a good model of the environment then plans with it
Two Main PlaNet improvements:
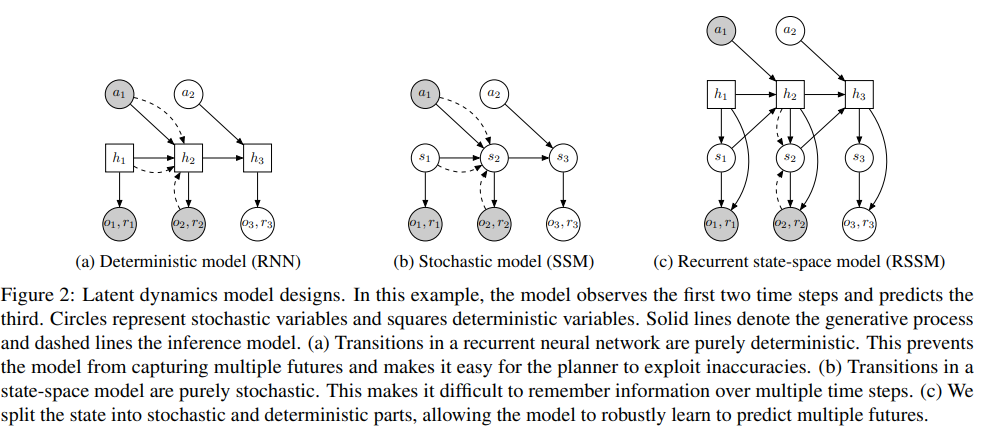

1.
Deterministic part
Stochastic part
PlaNet
PlaNet builds a good model of the environment then plans with it
Two Main PlaNet improvements:
2.
KL-loss
Reconstruction Loss

PlaNet vs MemUP
Similarities:
- Learning a good model in POMDP includes learning a good memory
- Learns by predicting more than 1 step into future
Differences:
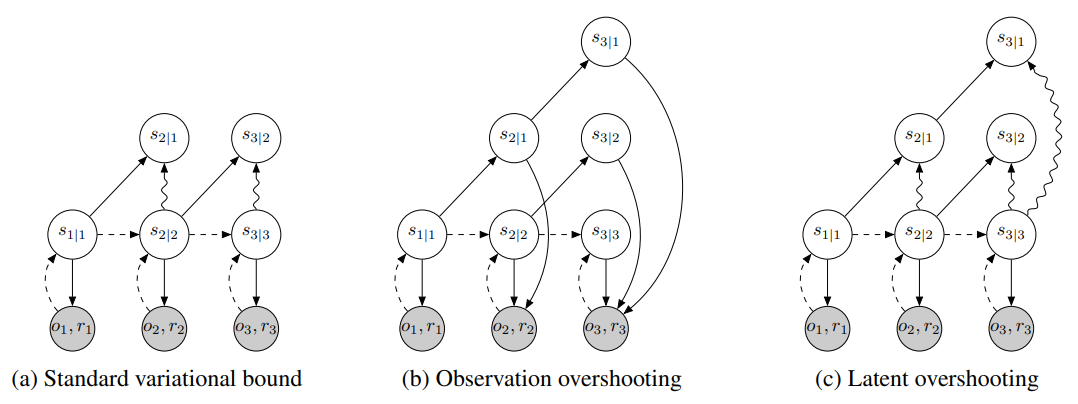
PlaNet's Model:
- Latent overshooting: prediction for the next N steps
- Generate for all intermediate steps in prediction horizon
- Focus on short term predictions:
- plan 12 steps ahead,
- ?did not use Latent Overshooting?
MemUP:
- Predict for arbitrary distant future events
- No need to to make intermediate predictions
- Focus on long-term memory: 100, 1000 steps, etc.
BigBird
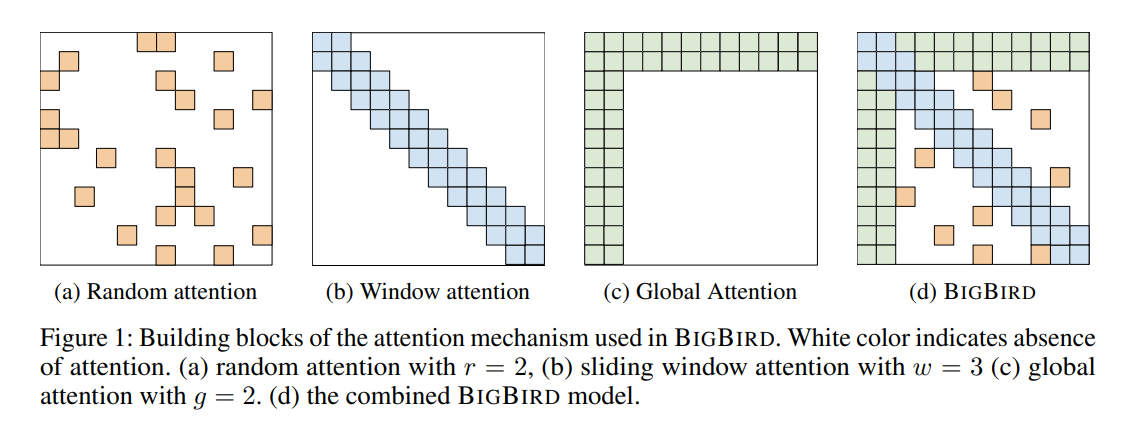
- Big Bird has Linear complexity in space instead of Quadratic complexity
- Can Process Longer Sequences
- Needs more Layers
Big Bird vs MemUP
Similarities:
- We fight the same problem
Differences (more like parallels):
Big Bird:
- Different Algorithms using different architectures
- Adds Global Tokens attending to everything
- Linear complexity in Space for each gradient update
- Quadratic complexity for each sequence
MemUP:
- Different Algorithms using different architectures
- "Selects some of the tokens that attend to everything"
- Constant complexity in Space for each gradient update
- Linear complexity for each sequence
Further Research Prespectives 1/2
Problems with Current Implementation:
-
Two-Phase Learning Process in RL
- There are some concerns but we probably can train memory and policy in parallel
- Different Prediction Targets
- Try to predict next observation, next reward
Appilcation to Other Domains:
-
Offline Reinforcement Learning
- No need to fix two-phase learning
-
Supervised Learning: NLP tasks in particular
- Core Idea behind MemUP is independent of RL specific properties
- No need to fix two-phase learning
Further Research Prespectives 2/2
Major Research Directions:
-
Fight with Noisy-TV problem
- Estimate Epistemic (reducible) and Aleatoric (irreducible) Entropy
- Estimating entropy reduction progress
- Combining MemUP with Transformer Archtechures
- Select which observations/tokens to store in transformer's attention window
- Local context is processed by transformer while MemUP based memory process long-term dependencies
-
Online Learning (only for RL applications)
- Learn memory/model in parallel with policy
-
Meta-Learning Applications
- Adapt to new tasks by selecting and storing samples with maximal MI for this task

Implementation Details
MemUP data Ёлка
By supergriver
MemUP data Ёлка
- 603



