MProve+

Privacy Enhancing Proof of Reserves for Monero

A. Dutta\(^{\dagger}\), Suyash Bagad\(^{\star}\), S. Vijayakumaran\(^{\dagger}\)

\(^{\dagger}\)Department of Electrical Engineering, IIT Bombay

Monero Konferenco 2023

June 23, 2023

\(^{\star}\)Aztec Protocol

Exchanges

  • Not your key, not your coins!
  • Cryptocurrency exchanges store your private keys
    • \(\color{lightgreen}{\text{Good:}}\) Seamless onboarding, trading
    • \(\color{red}{\text{Bad:}}\) Hacks, frauds, exit scams, fractional reserves! 

Solutions

  • Hardware wallets
    • Hard to use for general masses
    • Credit cards as HW wallets? Long way to go
  • Proof of solvency for exchanges:
  • Sensitive exchange data revealed
  • Still possible for public blockchains
  • What about Monero?
  • Hint: \(C^{\textcolor{lightgreen}{\text{Assets}} }\cdot C^{-\textcolor{red}{\text{Liabilities}}}>1\)
\textcolor{lightgreen}{\text{Assets}} - \textcolor{red}{\text{Liabilities}} \ge 0

BNB

USDC

BUSD

BTC

ETH

USDT

Source: https://www.binance.com/en/blog/community/our-commitment-to-transparency-2895840147147652626

Challenges in

  • Proof of reserves with privacy is hard
  • A Monero tx hides the spending address using ring signatures 
  • For a public key \(P=xG,\) we define key-image: \(I = xH(P)\)
  • A ring signature \(\sigma\) over \(\{P_1, P_2, \dots, P_{11}\}\) proves:
    • The tx sender owns one of the public keys in the ring
    • The key image \(I\) helps detect double-spending
  • Idea: Prove that we own multiple UTXOs from a large set of keys
1
2
3
4
5
6
7
8
9
10
11

MProve

\mathcal{P}_{\text{own}}
  • Suppose the exchange owns five addresses on Monero
  • It chooses an anonymity set to hide its addresses

MProve

\mathcal{P}_{\text{anon}}
1
2
3
4
5
6
7
8
9
10
12
11
13
  • Suppose the exchange owns five addresses on Monero
  • It chooses an anonymity set to hide its addresses
C_i = g^{\textcolor{orange}{y_i}} \cdot h^{\textcolor{red}{a_i}}
C'_i = \begin{cases} g^{\textcolor{orange}{z_i}} & P_i\in\mathcal{P}_{\text{own}} \\ g^{\textcolor{orange}{z_i}} \cdot C_i & P_i\notin\mathcal{P}_{\text{own}} \end{cases}
  • For each address \(P_i\in\mathcal{P}_{\text{anon}},\) the commitment is:
  • For each address it owns \(P_i\in\mathcal{P}_{\text{own}},\) it knows \((\textcolor{orange}{y_i}, \textcolor{red}{a_i})\)
  • It computes modified commitment s.t. \(\textcolor{orange}{z_i}\leftarrow \mathbb{F}\)

MProve

\mathcal{P}_{\text{anon}}
1
2
3
4
5
6
7
8
9
10
12
11
13
C_i = g^{\textcolor{orange}{y_i}} \cdot h^{\textcolor{red}{a_i}}
C'_i = \begin{cases} g^{\textcolor{orange}{z_i}} & P_i\in\mathcal{P}_{\text{own}} \\ g^{\textcolor{orange}{z_i}} \cdot C_i & P_i\notin\mathcal{P}_{\text{own}} \end{cases}
C_i\cdot C_i^{'-1} = \begin{cases} g^{\textcolor{orange}{y_i - z_i}} \cdot h^{\textcolor{red}{a_i}} & P_i\in\mathcal{P}_{\text{own}} \\ g^{\textcolor{orange}{z_i}} & P_i\notin\mathcal{P}_{\text{own}} \end{cases}

// commitment to amount \(\color{red}{a_i}\)

// commitment to amount \(\color{red}{0}\)

\prod_{i\in [n]} C_i\cdot C_i^{'-1} = g^{\textcolor{orange}{\dots}} \cdot h^{\textcolor{red}{\sum_j a_j}}

// commitment to total reserves \(\color{red}{\sum_ja_j}\)

  • We still need to prove that \(C'_i\) was correctly computed

MProve

\mathcal{P}_{\text{anon}}
1
2
3
4
5
6
7
8
9
10
12
11
13
C'_i = \begin{cases} g^{\textcolor{orange}{z_i}} & P_i\in\mathcal{P}_{\text{own}} \\ g^{\textcolor{orange}{z_i}} \cdot C_i & P_i\notin\mathcal{P}_{\text{own}} \end{cases}
\implies \text{keypair:} \left(\textcolor{orange}{z_i}, \ C'_i\right)
\implies \text{keypair:} \left(\textcolor{orange}{z_i}, \ C'_iC^{-1}_i\right)
  • Thus, we can compute a ring signature such that: 
\gamma_i \leftarrow \left(\textcolor{lightgreen}{C'_i}, \ \ \textcolor{orange}{C'_i \cdot C_i^{-1}}\right)
  • Still need to prove that already-spent addresses were not used 
\sigma_i \leftarrow \left(\textcolor{lightgreen}{P_i}, \ \ \textcolor{orange}{C'_i\cdot C_i^{-1}}\right)

// regular ring signature

// linkable ring signature

Drawbacks of MProve

  • Scales linearly in the size \(n\) of the anonymity set
  • Adds limits on the size of the anonymity set
  • The linkable ring signatures reveal the key image \(I^{\star}\) of \(P_i\in\mathcal{P}_{\text{own}}\)
  • A future transaction from \(P_i\) will reveal the same key image \(I^{\star}\)
  • Harms privacy of the exchange in the future

MProve+

1
2
3
4
5
6
7
8
9
10
12
11
13
0
1
0
0
0
0
0
0
0
0
0
0
0
(
)
\textbf{e}_1 =
0
0
0
0
0
1
0
0
0
0
0
0
0
(
)
\textbf{e}_2 =
0
0
0
0
0
0
0
0
1
0
0
0
0
(
)
\textbf{e}_3 =
0
0
0
0
0
0
0
0
0
1
0
0
0
(
)
\textbf{e}_4 =
0
0
0
0
0
0
0
0
0
0
0
0
1
(
)
\textbf{e}_5 =
y_1
y_2
y_3
y_4
y_5
(
)
\textbf{y} =
a_1
a_2
a_3
a_4
a_5
(
)
\textbf{a} =
C_1
C_2
C_3
C_4
C_5
C_6
C_7
C_8
C_9
C_{10}
C_{11}
C_{12}
C_{13}
(
)
\textbf{C} =
P_1
P_2
P_3
P_4
P_5
P_6
P_7
P_8
P_9
P_{10}
P_{11}
P_{12}
P_{13}
(
)
\textbf{P} =

MProve+

1
2
3
4
5
6
7
8
9
10
12
11
13
0
1
0
0
0
0
0
0
0
0
0
0
0
\textbf{e}_1
C_1
C_2
C_3
C_4
C_5
C_6
C_7
C_8
C_9
C_{10}
C_{11}
C_{12}
C_{13}
(
)
\textbf{C} =
\implies \textbf{C}^{\textbf{e}_j} = g^{\textcolor{orange}{y_j}} \cdot h^{\textcolor{red}{a_j}}
\implies \textbf{P}^{\textbf{e}_j} = g^{\textcolor{orange}{x_j}}
\implies \textbf{H}_P^{\textbf{e}_j} = I_j^{\textcolor{orange}{x_j^{-1}}}
  • Pattern: vectorise all the relations and combine into one equation
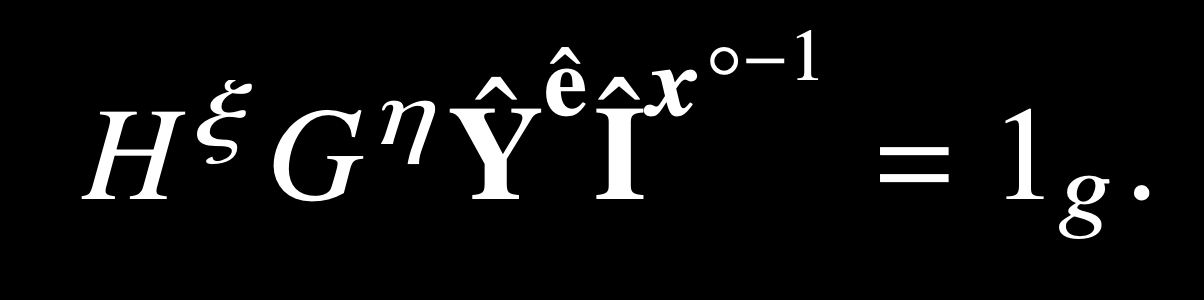
\implies \left(\textbf{C} \circ \textbf{P}^u \circ \textbf{H}_P^{u^2}\right)^{\textbf{e}_j} = g^{\textcolor{orange}{\langle ., . \rangle}} h^{\textcolor{red}{\langle ., . \rangle}} \textbf{I}^{\textcolor{green}{\langle ., . \rangle}}

MProve+

1
2
3
4
5
6
7
8
9
10
12
11
13
  • Pattern: vectorise all the relations and combine into one equation
\implies \left(\textbf{C} \circ \textbf{P}^u \circ \textbf{H}_P^{u^2}\right)^{\textbf{e}_j} = g^{\textcolor{orange}{\langle ., . \rangle}} h^{\textcolor{red}{\langle ., . \rangle}} \textbf{I}^{\textcolor{green}{\langle ., . \rangle}}
  • We can then use inner product argument of the form:
PoK \left\{ (\textbf{a}, \textbf{b}) \in \mathbb{Z}_q^N \ | \ P = u^{c}\textbf{g}^{\textbf{a}} \textbf{h}^{\textbf{b}} \wedge c = \langle \textbf{a}, \textbf{b} \rangle \ \right\}
  • Proof size in an inner product argument is \(\mathcal{O}(\text{log}(N))\)
  • MProve+ proof size \(\approx (n + s + \text{log}(ns))\) vs MProve was \(\approx 12n\)

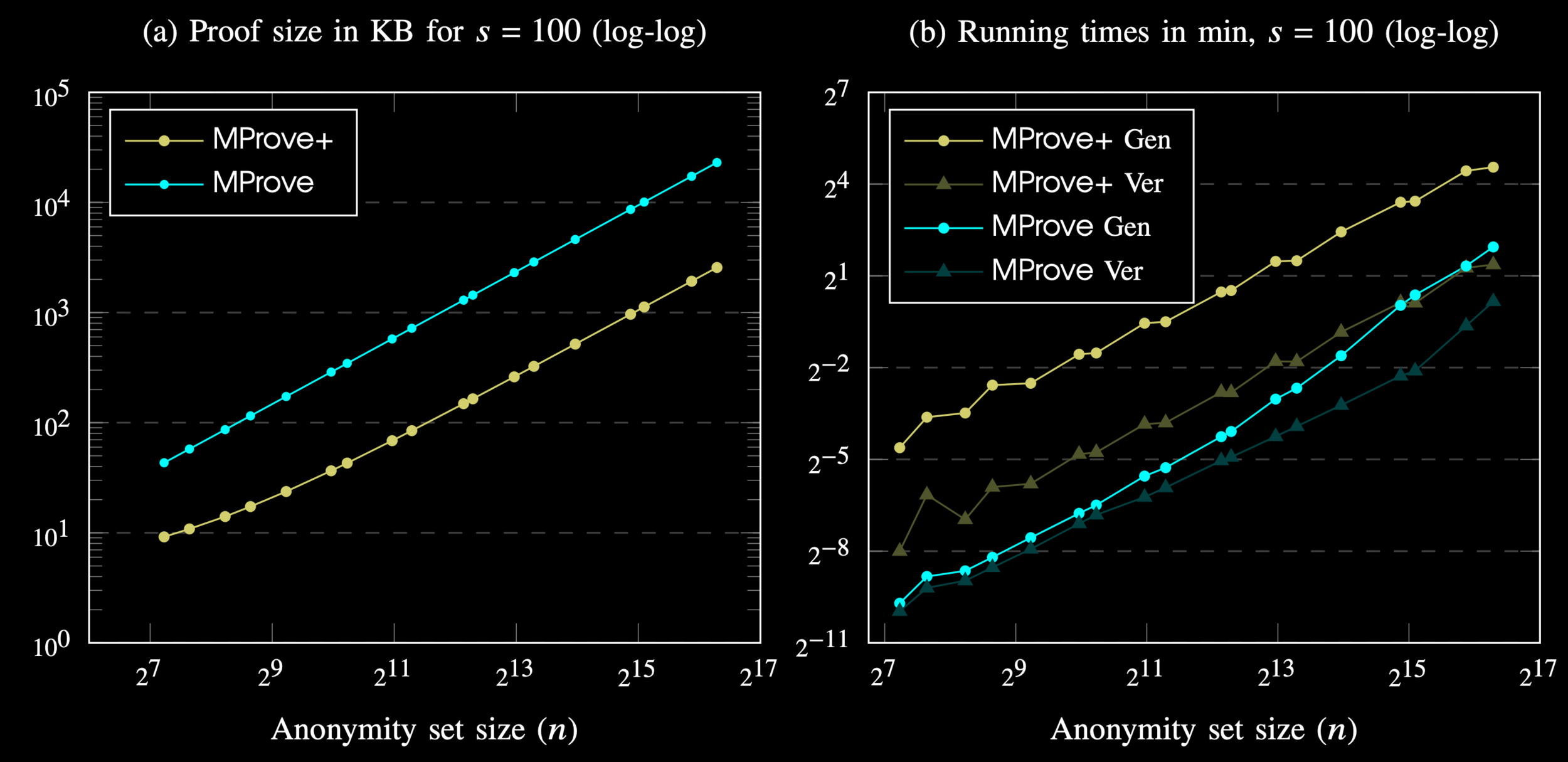
Performance

  • MProve+ proofs are \(\ge 8\text{x}\) shorter that that of MProve 
  • MProve+ proof generation is \(4-6\text{x}\) slower than MProve
  • MProve+ proof verification is \(8\text{x}\) faster than proof generation
n \ \longrightarrow
n \ \longrightarrow
\text{Proof size in KB} \longrightarrow

Note: All plots are in log-log scale.

\text{Time in min} \longrightarrow

Future work

  • MProve+ solves the key-image linkability of MProve
  • MProve+ proof sizes are much smaller than MProve
  • Thus, running MProve+ is possible for exchanges
  • But is it practical?
    • For \(n=50000\) the it takes \(\approx 2\) hours to generate a proof using an 2.6GHz i7 computer
    • Impractical to include all of UTXOs as anon set
    • Our group from IIT Bombay is working on Monero proof of reserves using Nova proof system

References

  1. Proof of concept in Rust: https://github.com/suyash67/MProvePlus-Ristretto

  2. Proof of concept in Monero source code: https://github.com/harshitgupta412/monero/blob/MProvePlus/

MProvePlus at Monerokon 2023

By Suyash Bagad

Made with Slides.com

MProvePlus at Monerokon 2023

MProve+ presentation at Monerokon 2023.

  • 31

More from Suyash Bagad