Learning to Coordinate
with Coordination Graphs
in Repeated
Single-Stage Multi-Agent
Decision Problems
Eugenio Bargiacchi, Timothy Verstraeten, Diederik Roijers, Ann Nowé, Hado van Hasselt
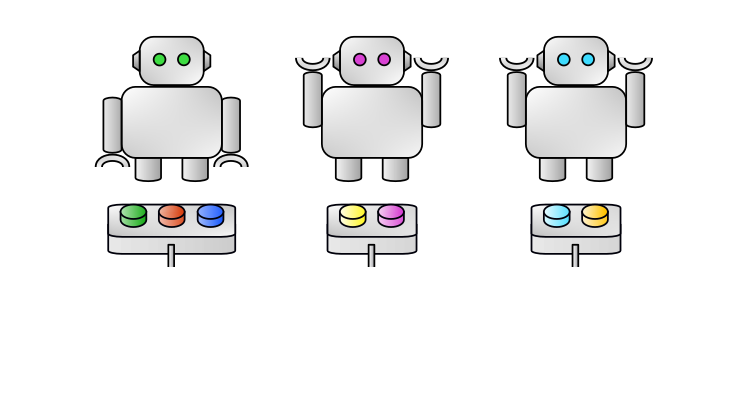
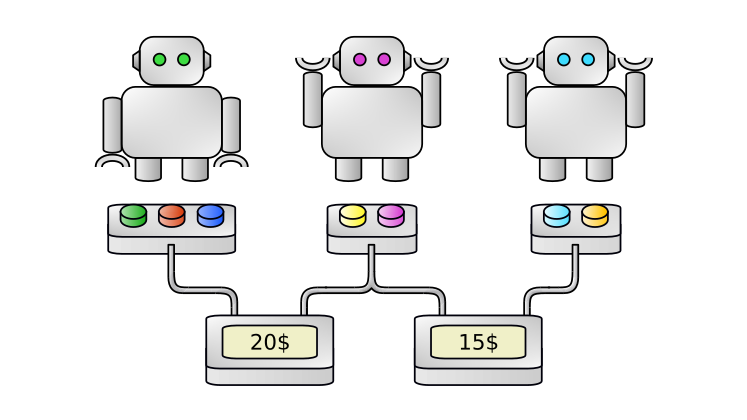
Possible approach: UCB
Does not scale with AN Exponential NUMBER OF joint actions
\hat\mu_i
\sqrt{2\frac{\log{n}}{n_i}}
LEARNED JOINT ACTION AVERAGE
JOINT ACTION EXPLORATION BONUS
+
OUR CONTRIBUTION: MAUCE
\hat\mu_e
\frac{(r^e_{\max})^2}{n_t^e}
LEARNED LOCAL JOINT ACTION AVERAGE
LOCAL JOINT ACTION EXPLORATION BONUS
MAXIMIZE:
\sum\limits_e\hat\mu_e + \sqrt{\frac{\log(tA)}{2}(\sum_e\frac{(r^e_{\max})^2}{n_t^e})}
OUR CONTRIBUTION: MAUCE
<\hat\mu_e, \frac{(r^e_{\max})^2}{n_t^e}>
-
WE INTRODUCE UCVE, A VARIABLE ELIMINATION-type Algorithm
-
prune suboptimal local joint actions, reducing the number of joint actions to consider.
VECTOR REPRESENTATION:(objectives)
variable elimination
variable elimination
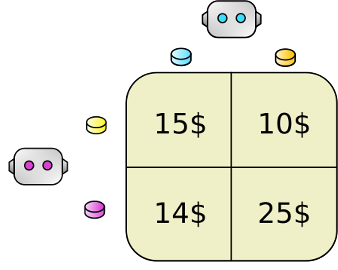
variable elimination
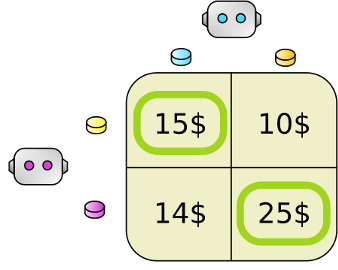
variable elimination
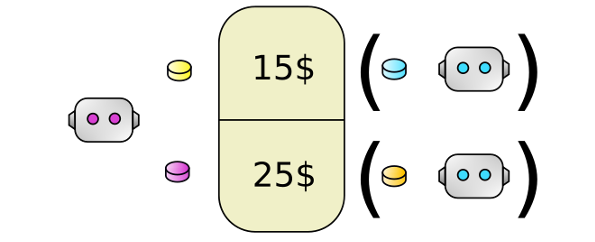
variable elimination
OUR CONTRIBUTION: MAUCE
<\hat\mu_e, \frac{(r^e_{\max})^2}{n_t^e}>
-
WE INTRODUCE UCVE, A VARIABLE ELIMINATION-type Algorithm
-
prune suboptimal local joint actions, reducing the number of joint actions to consider.
VECTOR REPRESENTATION:(objectives)
OUR CONTRIBUTION: MAUCE
\sqrt{\frac{\log(tA)}{2}(\sum_e\frac{(r^e_{\max})^2}{n_t^e})}
Exploration bonus bounds regret
linear in the number of agents!
Experiments
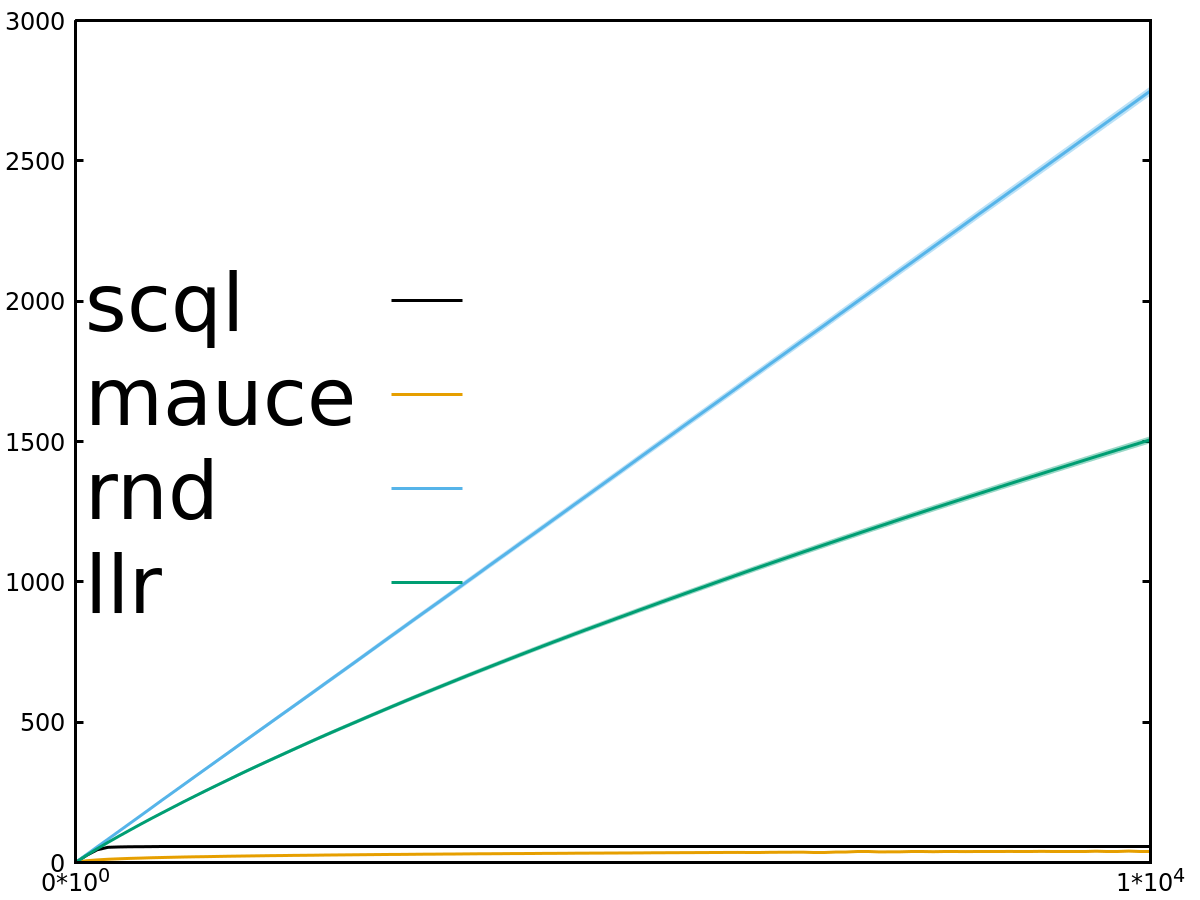
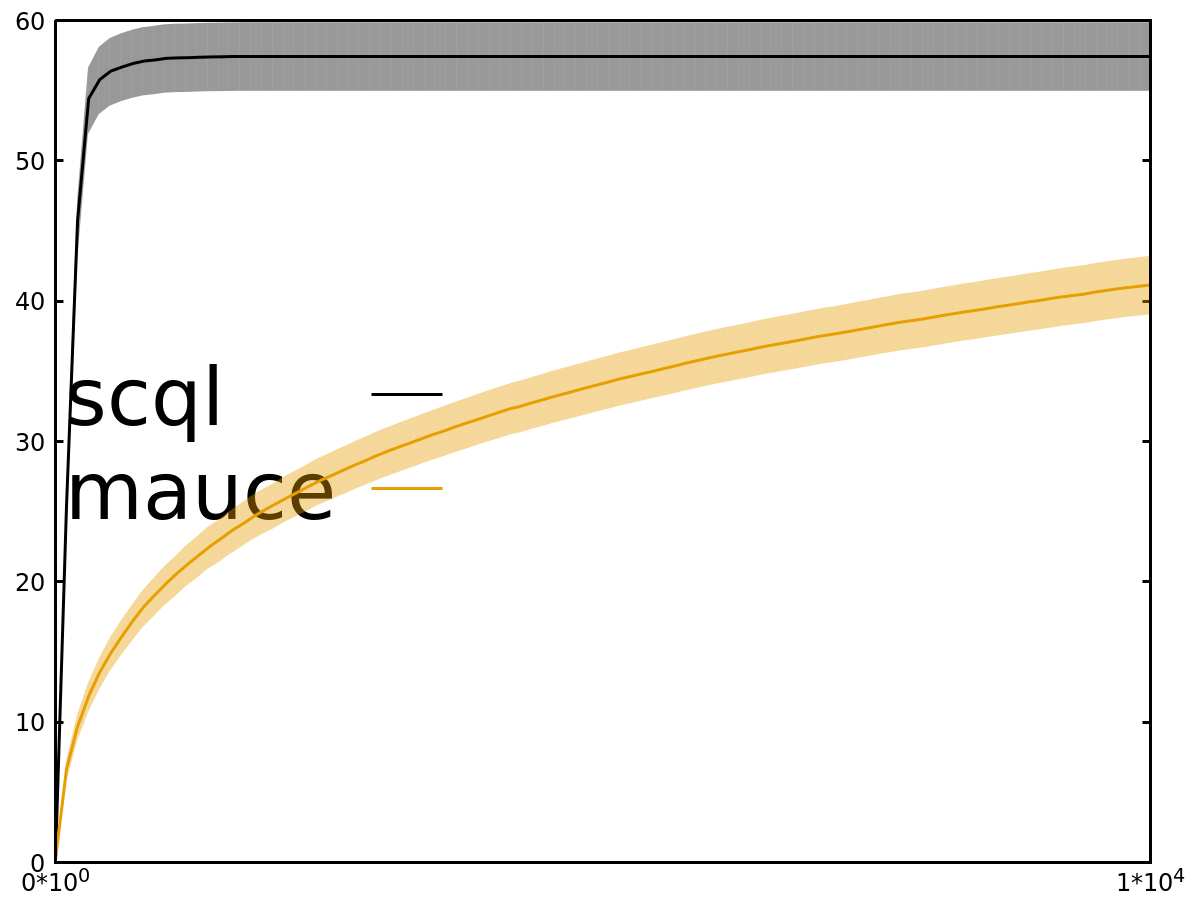
- Regret x Timesteps (lower is better)
We have similar results for other experiments:
- Mines benchmark from Multi Objective literature
- Windmill setting using realistic wind and turbulence simulator
All code released open source!
QUestions?
thank you!
BENERL 2018
By svalorzen
