数学と表現
クリエイティブコーディングの世界
どうも
HIGA

Enginner
クリエイティブ
コーディングとは
Section.1
Creative coding is a type of computer programming in which the goal is to create something expressive instead of something functional. It is used to create live visuals and for VJing, as well as creating visual art and design, entertainment, art installations, projections and projection mapping, sound art, advertising, product prototypes, and much more.
クリエイティブコーディングとは、機能的なものではなく表現力豊かなものを作成することを目的とするコンピュータープログラミングの一種です。 ライブビジュアルの作成やVJの作成、ビジュアルアートとデザイン、エンターテイメント、アートインスタレーション、プロジェクションとプロジェクションマッピング、サウンドアート、広告、製品プロトタイプなどの作成に使用されます。
表現するための
プログラミング
たとえば
ジェネラティブアート
データビジュアライゼーション
ポストエフェクト
デモシーン
などがあります
その強みとは
Section.2
1. データとの親和性
2. プロシージャル
3. 特異な表現力
データとの親和性
-
データを取得できればビジュアライズ可能
-
マウス、カメラ、音などリアルタイムに反応

プロシージャル
-
手続き型のことで数式や処理を組み合わせ操作
-
数値の調整や処理の組み換えによる変更容易性
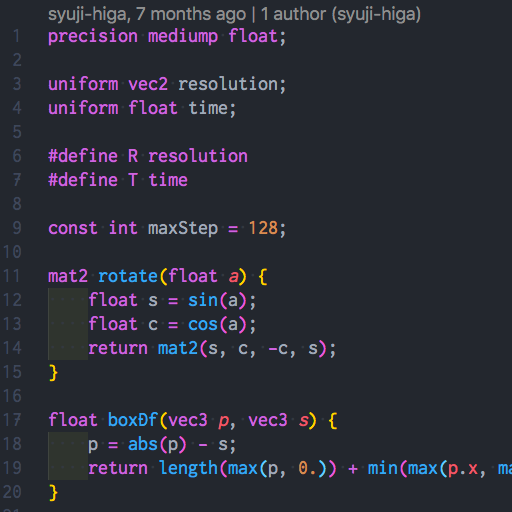
特異な表現力
-
数学的な表現につよい


ひとつづつをみると
クリエイティブコーディングを
選ぶ必要性を感じないかも
「それ他の方法でできるのでは?」
「今どきのツールはプロシージャルな部分も多いよ」
「リアルタイムだとクオリティ低くならない?」
「プログラムなんて大変でしょ」
「自由に描くことは難しいよね?」
「工数が増えるのでは?」
まあ、それはある
だが、ツールも色々あるし
それらの強みを合わせて考えると
その良さを感じとれる
クリエイティブコーディングとは、機能的なものではなく表現力豊かなものを作成することを目的とするコンピュータープログラミングの一種です。 ライブビジュアルの作成やVJの作成、ビジュアルアートとデザイン、エンターテイメント、アートインスタレーション、プロジェクションとプロジェクションマッピング、サウンドアート、広告、製品プロトタイプなどの作成に使用されます。
要は適材適所で
クリエイティブコーディングも
それに当てはまるという話
まあ、そんなことより
クリエイティブコーディングは
たのしい
だから今日は
俺の話を聞いてくれ!
なにで作るのか
Section.3
1. コードベース
2. ビジュアルベース
コードべース
ビジュアルべース
インストールが億劫な
そんな面倒くさがりの人には
コードベース
ビジュアルベース
Webできるプラットフォーム
いつだって
今すぐにだって始められる
ということで
数学からみる表現
Section.4
と題して
本日の一番伝えたいことを
お話しします
コンピュータを使っている以上
どんな内容であろうと結局は
数学的な計算が行われていることに
かわりはありません
普段それを意識することは少ないが
クリエイティブコーディングでは
描画に関する計算を
直接的におこなうことが基本
つまり、数学を制することは
クリエイティブを制する
それは
直接コードを書くことの少ない
ビジュアルベースのプログラミングでも
数学的な思考は大いに役立つ
とは言っても
数学は難しい思う方もいるかも
私もけっこう苦手
とりあえず、今日のところは
考えるな、感じろ
それでは
数学からみる様々な表現を
数学の時間はいつも寝ていた私と一緒に
いろいろと見ていこう
数学から得られる表現
と
表現に使われている数学
2つの視点から見てみます
1. 座標系
2. 三角関数
3. ベクトルと行列
数学から得られる表現
1. 座標系
主な座標系は2つ
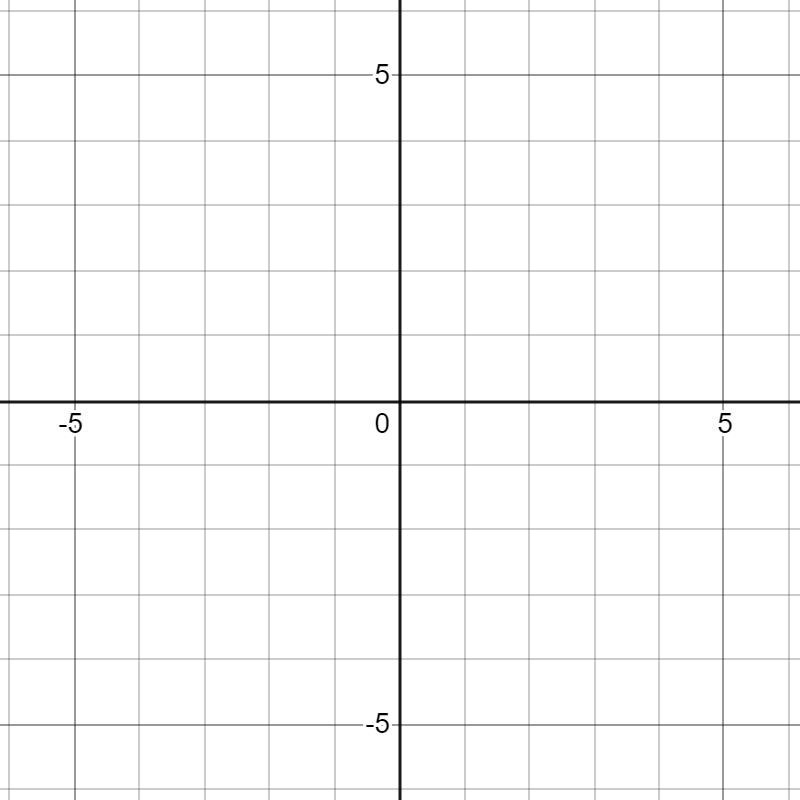
直交座標系
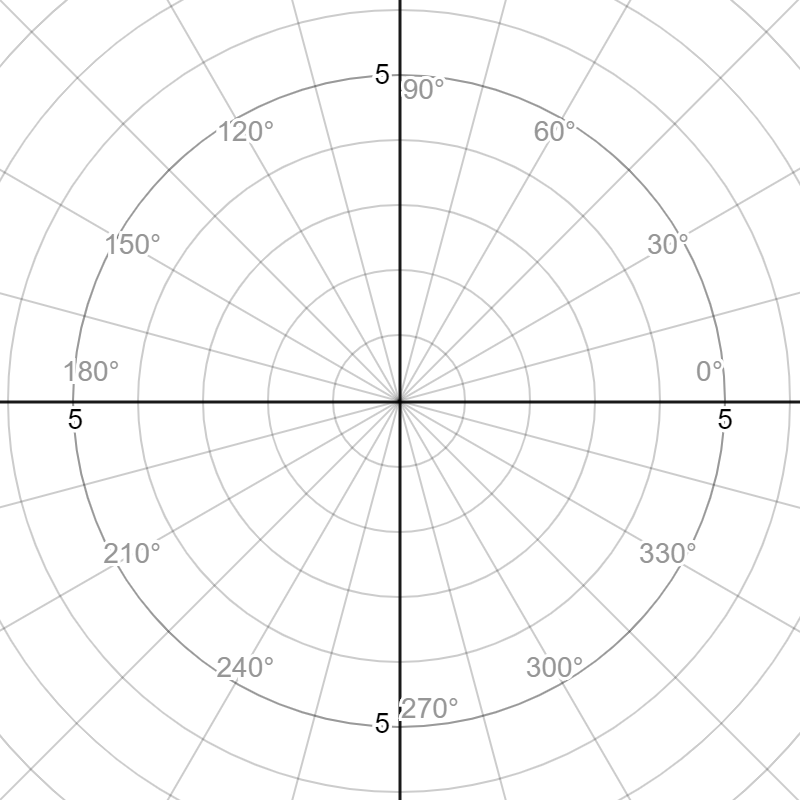
極座標系
直交座標系


極座標系
a
原点からのそれぞれの軸における距離で求める
3
2
(x, y)
(r, θ)
つまり a = (3, 2) となる
原点からの距離と角度で
求める
b
つまり b = (4, 30°) となる
4
30°
X座標とY座標がわかれば
三平方の定理により距離が
アークタンジェントにより角度が
わかる
つまり
直交座標系から極座標系へ
変換できる
直交座標系
極座標系


なぜ座標の話を
始めにしたのかというと
なにかに表示されている
または表示するということは
なんらかの座標系をもとに
考えなくては始まらない
その感覚を感じてもらえると
以降の話も理解しやすいかも
2. 三角関数
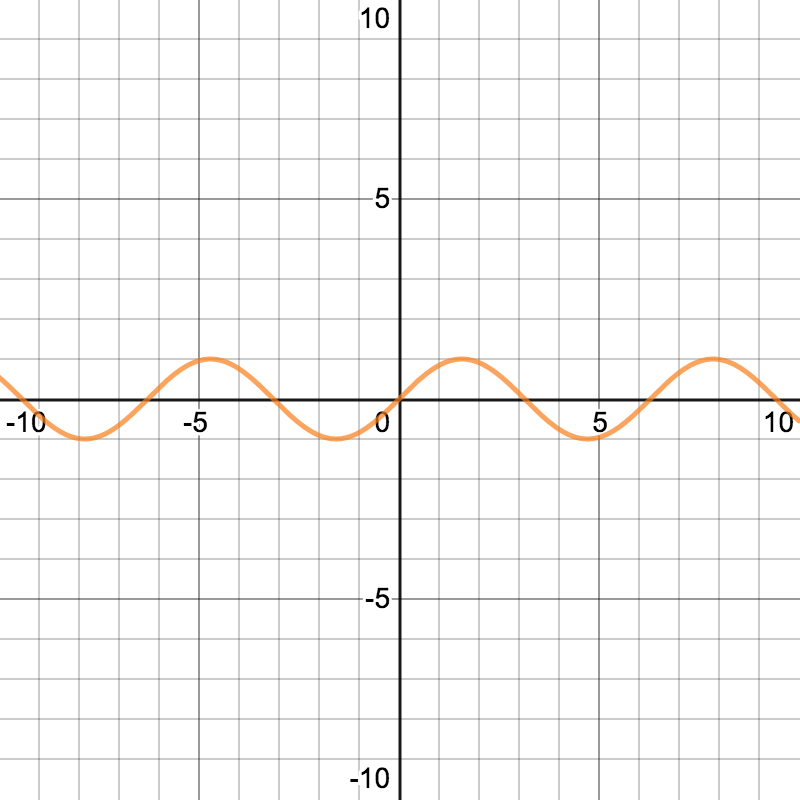
sin
cos
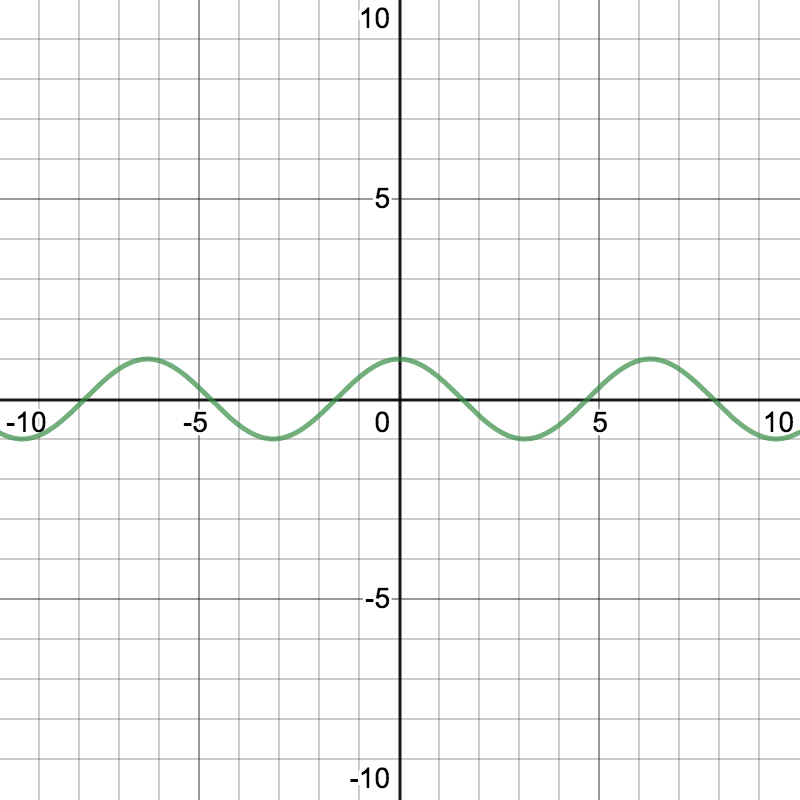
重ねると
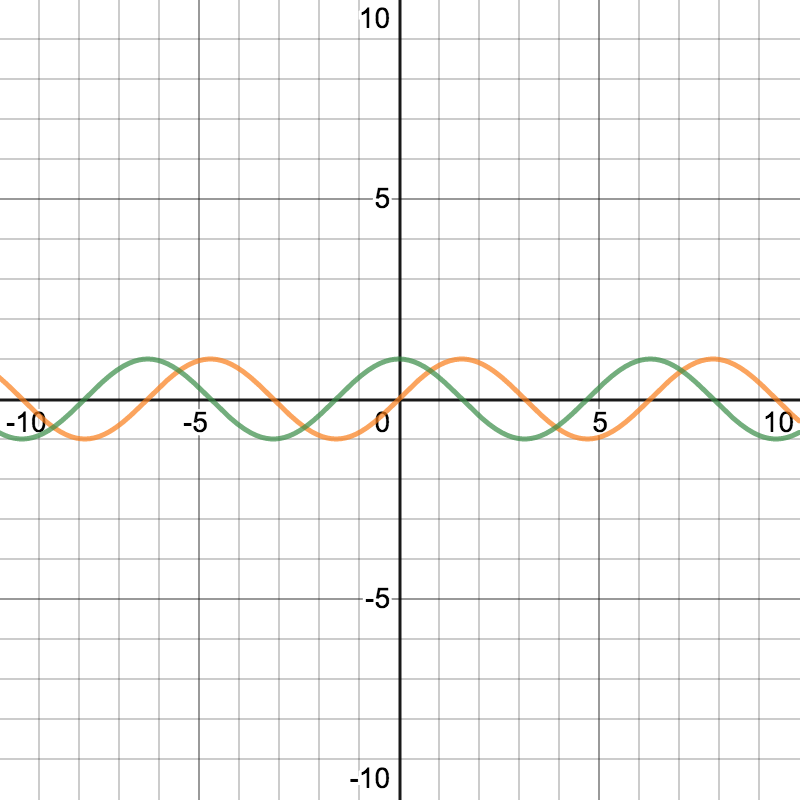
周期がズレている
のがわかる
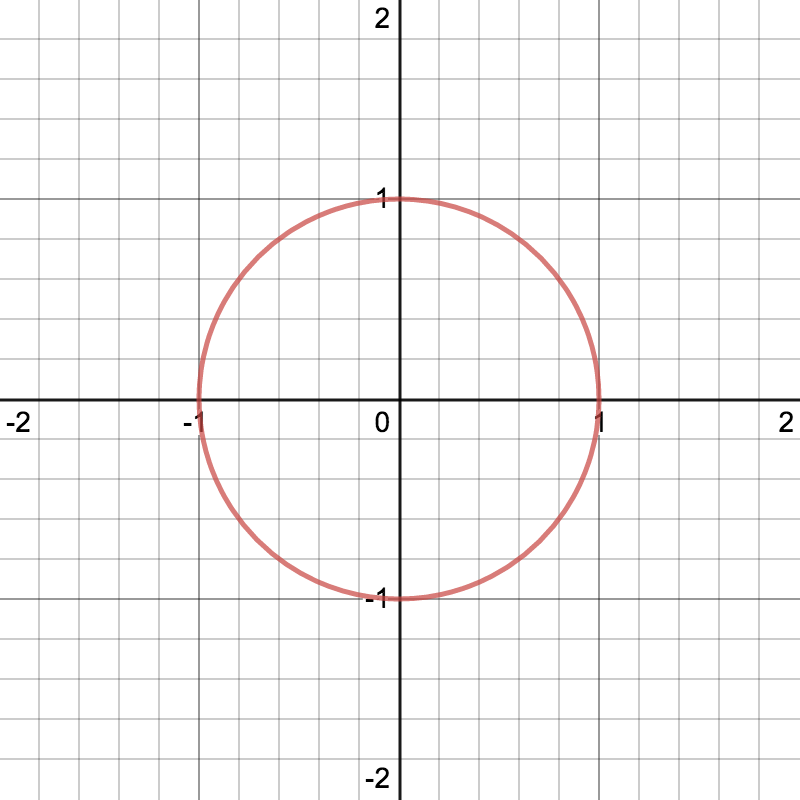
この性質を考えて
X軸 に sin の周期
Y軸 に cos の周期
を当てはめると
円を描いて動く

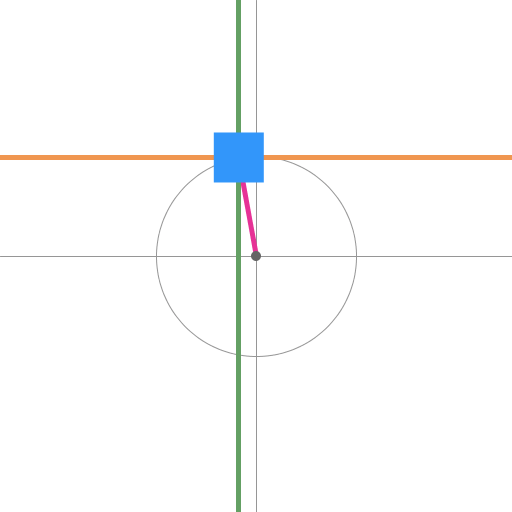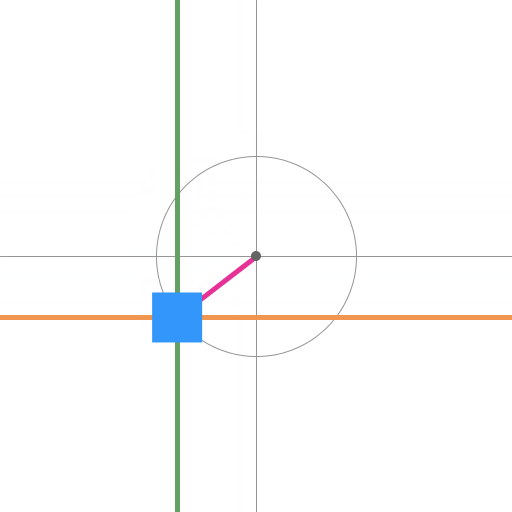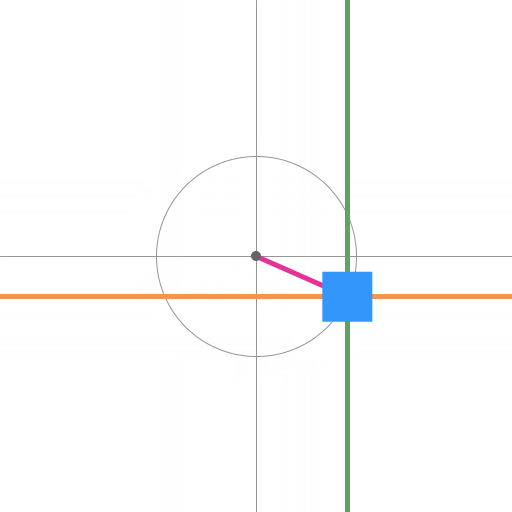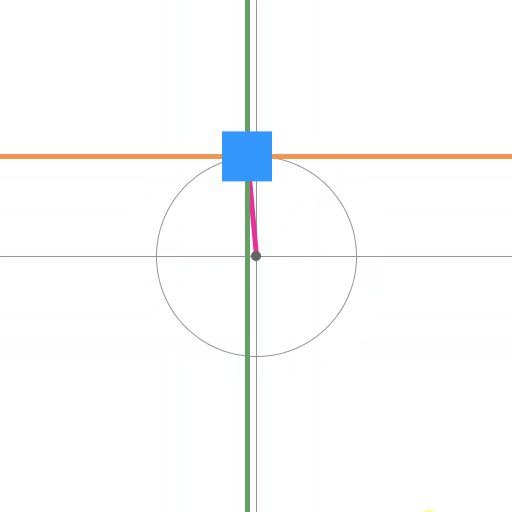
オレンジが X 軸で
sin の動き
グリーンが Y 軸で
cos の動き
美しいと思いませんか?
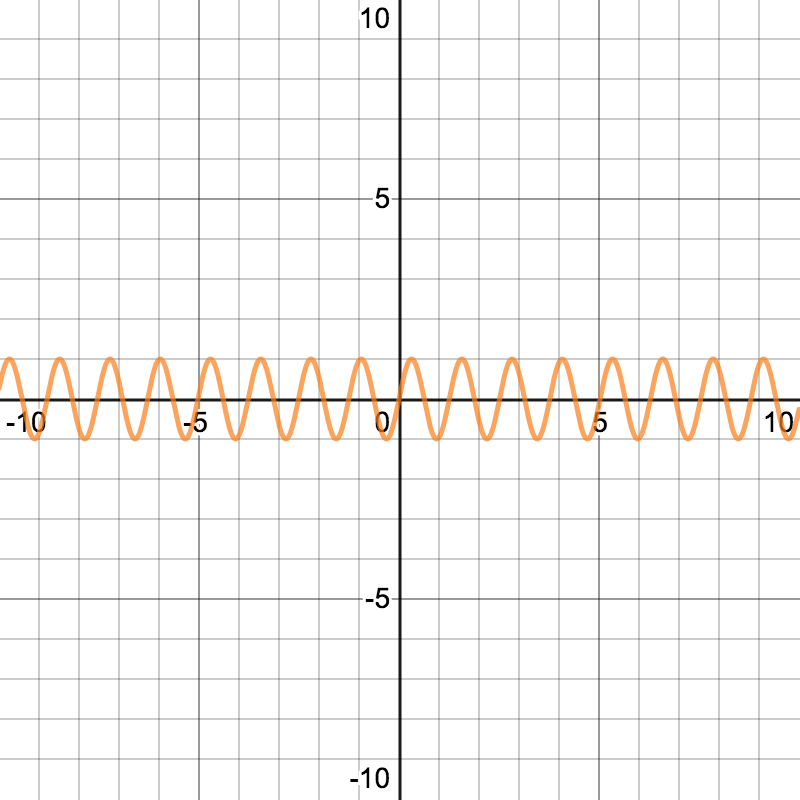
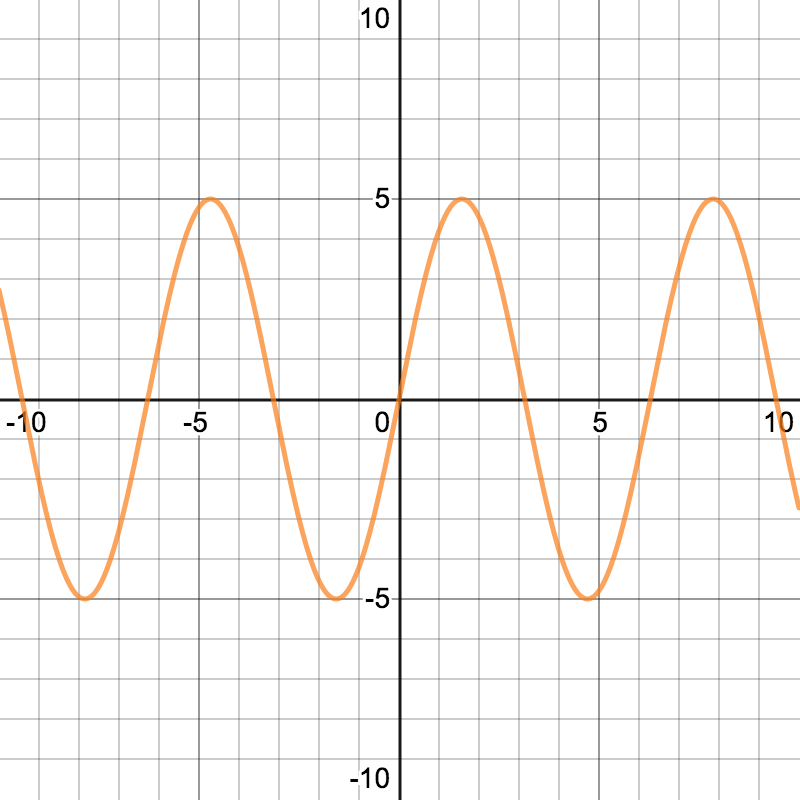
周期を変えたり
振幅を増減させたり
することも
簡単にできます
そして、それにより
さまざまな音がだせます
周波数 100 振幅 1
周波数 500 振幅 1
周波数 100 振幅 0.5
周波数 500 振幅 0.5
全く逆の振幅の音を用意すると
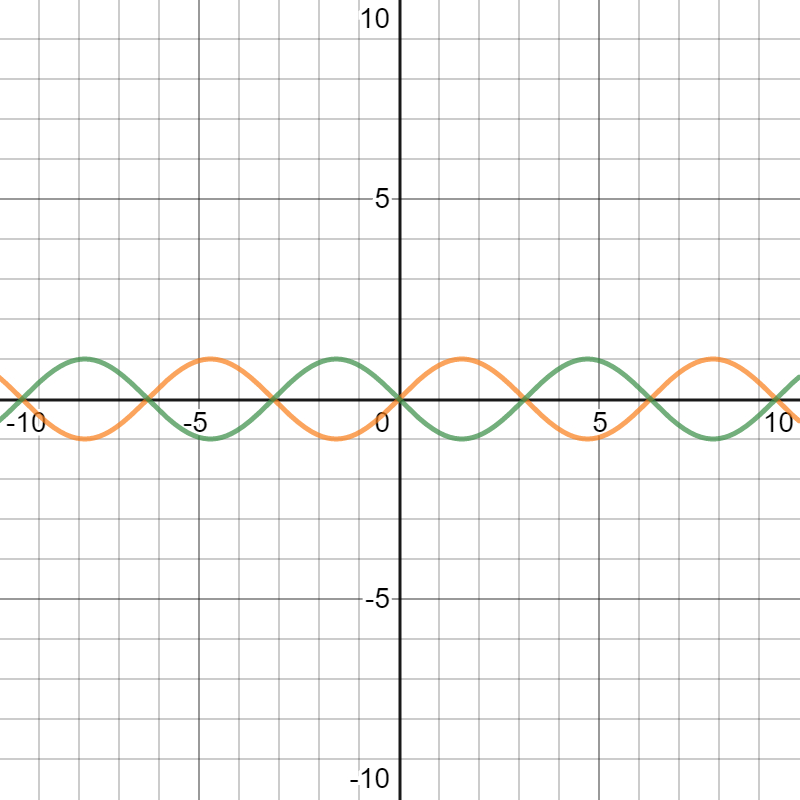
無音になります
面白いと思いませんか?
3. ベクトルと行列
ベクトルとは
向きと大きさの
要素をもった量

表し方は始点を原点として
(3, 4) と表せる
x = 4
y = 3
つまり
座標と同じ
実際プログラムでは
座標をベクトルで表したりする

画像で考えると
ピクセルごとの位置をベクトルとして格納


x = 0.4
y = 0.3
a
(0.3, 0.4) の
点 a のピクセルは
ベクトルとして
表せる
全てのピクセルの位置を
ベクトルで表せます
それがなんなんだ?
と、思うかもですが
先に行列について話す
行列とは
数などを矩形状に配列したもの
1 0 0
0 1 0
0 0 1
ベクトルに行列を作用できる
1 -1
0.5 1
4
2
=
2
4
1 -1
0.5 1
4
2
=
2
4
行列
ベクトル
✕
積

x = 4
y = 2
➡

x = 2
y = 4
これを画像の全てのピクセルで行うと
➡



矢印の先が指すピクセルの色は変わらない
➡




もしかしたら座標系を歪めている
と考えるとわかりやすいかも

➡
座標系の歪みによりベクトルが変化する


このように行列を使って
画像を変換できる
一般的な変換の行列には
公式があります
それを使えば




➡


➡


並行移動行列
拡大縮小行列

➡
回転行列


➡
シアー行列




それほど難しいものではないので
覚えてみるのもよいと思います
空間を自在に操れるって
かっこいいですよね
つぎは
1. ポストエフェクト
2. レイマーチング
表現に使われている数学
1. ポストエフェクト
ポストエフェクトとは
画面に効果を与えること
ビフォー
アフター

いくつかの効果がありますので
ひとつづつ紐解いてみます
ディストーション
これで画像のX軸をずらす
適応後
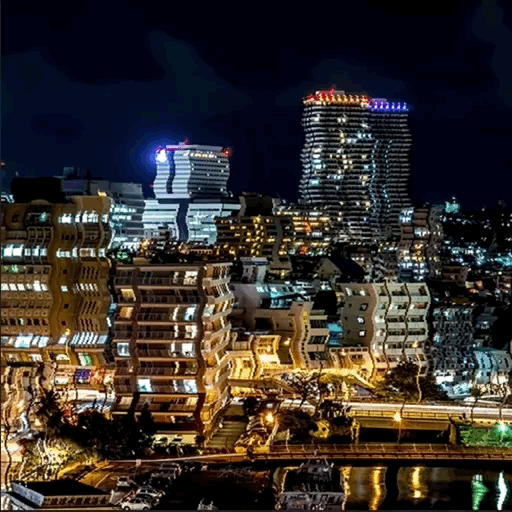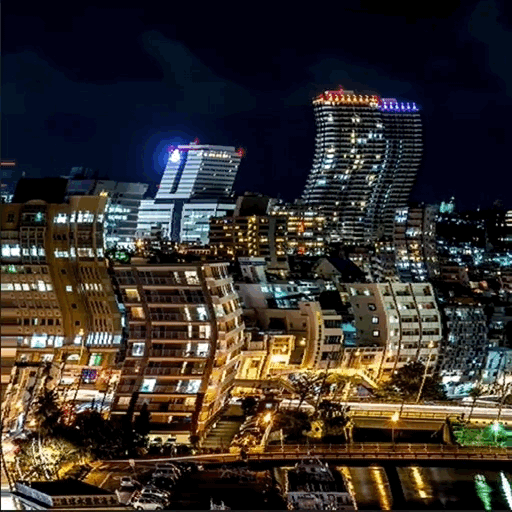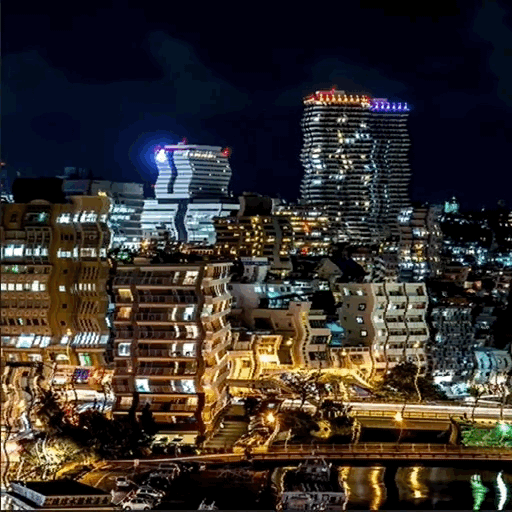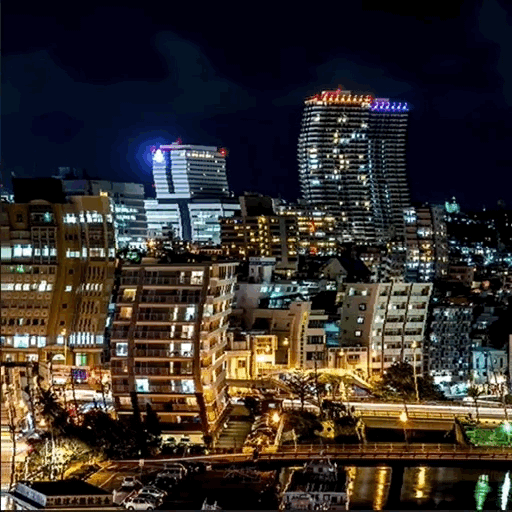

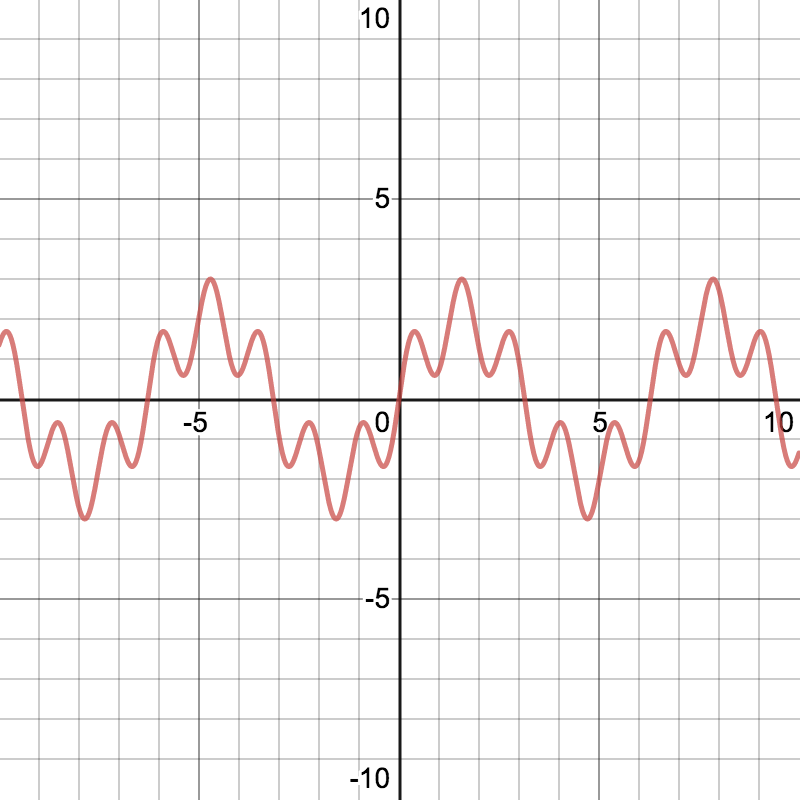
POINT. 三角関数の和
ホワイトノイズ
この色を足す
適応後


POINT. 乱数

ブロックノイズ
これで画像のX軸をずらす
適応後


POINT. 切り捨て
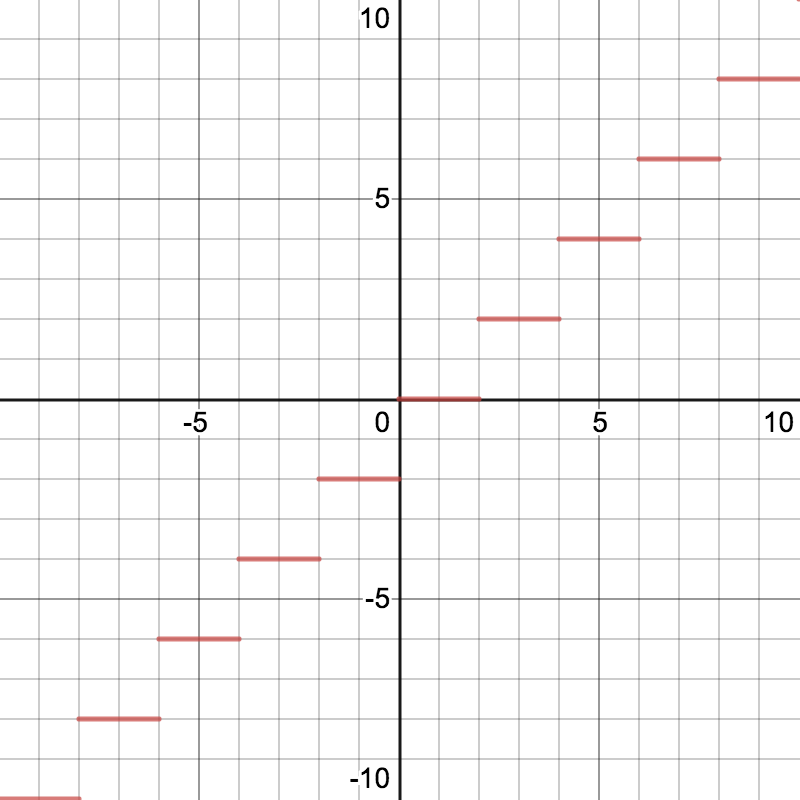
走査線
この色を引くする
適応後


POINT. 周期の短い三角関数
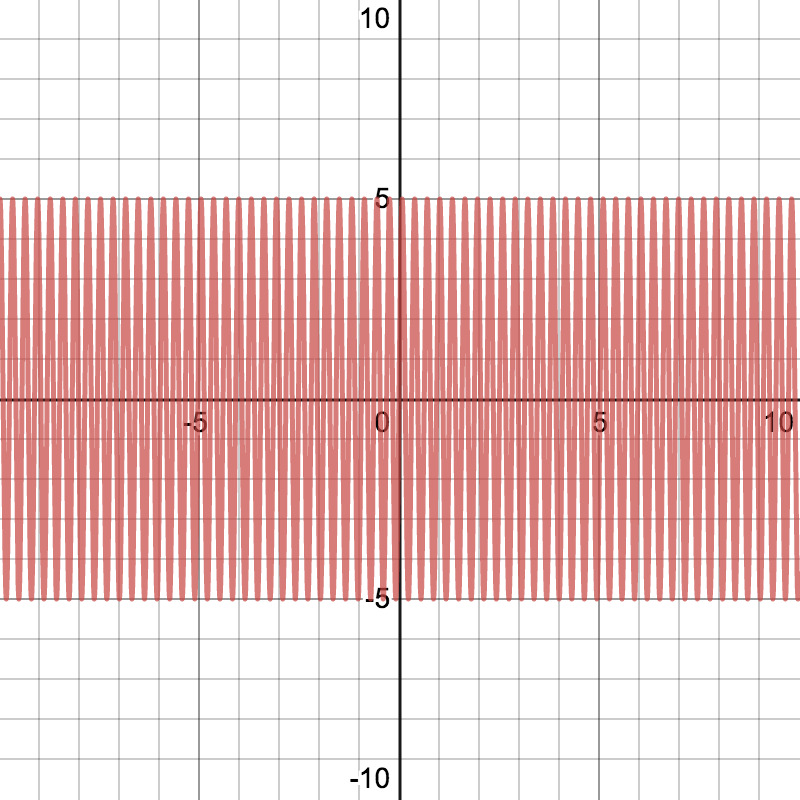
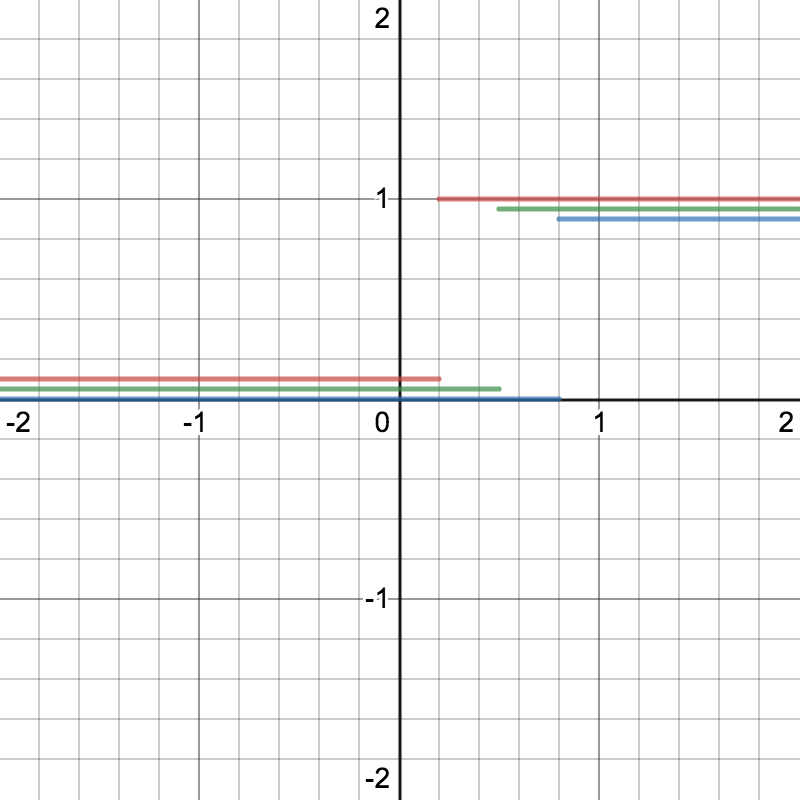
ポスタリゼーション
RGB ごとに二階調化
適応後


POINT. 二階調化
ビネット効果
この色を引く
適応後


POINT. 三平方の定理
もう一度みてみる
ビフォー
アフター

他にも様々なポストエフェクトがある
-
ノイズ
-
パーリンノイ
-
バリューノイズ
-
シンプレック
ノイズ -
セルラーノイズ
-
fBm
-
-
RGB シフト
-
モーションブラー
-
被写界深度
-
ブルーム
-
モザイク
-
モノクロ
-
アウトライン
etc...
さまざまな表現と
組み合わせやすい
無限に遊べる
2. レイマーチング
レイマーチングとは
3Dモデルなどのポリゴンを使わず
距離関数という式で
3Dオブジェクトを表示する方法
ゆえに
距離関数を制する者は
レイマーチングを制す
と言われている
✕ モデリングデータ
◯ 距離関数

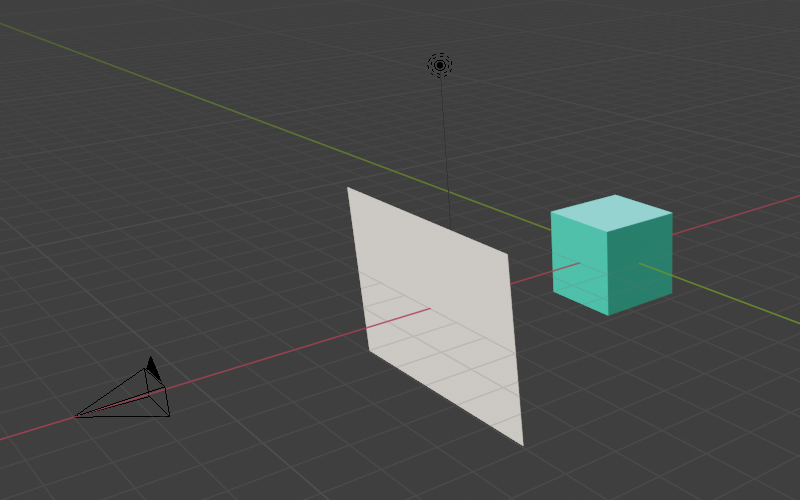
⬅ スクリーン
レイ(通過)⬇
⬆ レイ(衝突)
カメラ(視点)からレイ(光線)を放ち衝突判定
衝突判定に距離関数を使う
オブジェクトの形は原点からの距離で決める

原点
レイを段階的に進める
平面的にしたレイの軌道
カメラ
原点
スクリーン
オブジェクトまでの距離を取得し
カメラ
原点
オブジェクトの
原点からの距離
スクリーン
スクリーン通過点
レイとオブジェクトの衝突を判定して
カメラ
原点
衝突点
スクリーン
スクリーン通過点
距離が 0 になるまで繰り返す
このエリアはオブジェクトから離れてるので
距離は0より大きい
このエリアは
オブジェクト内なので
距離は0以下
カメラ
原点
衝突点
スクリーン
スクリーン通過点
現在のレイの位置から
オブジェクトへの距離を求める式が
距離関数
距離関数から生まれるのが
レイマーチング
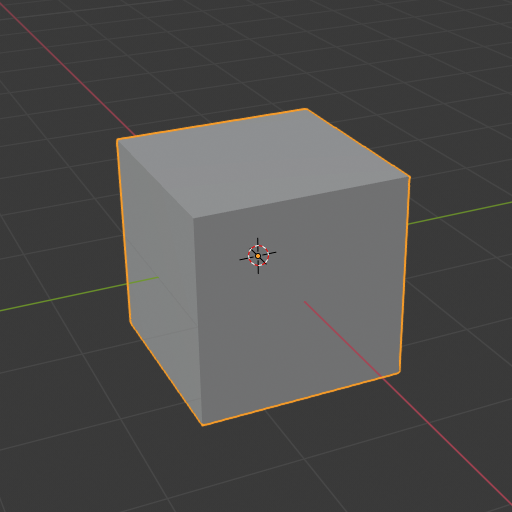
ボックスの距離関数では
絶対値や最大値などなど
形により様々な数式が使われる
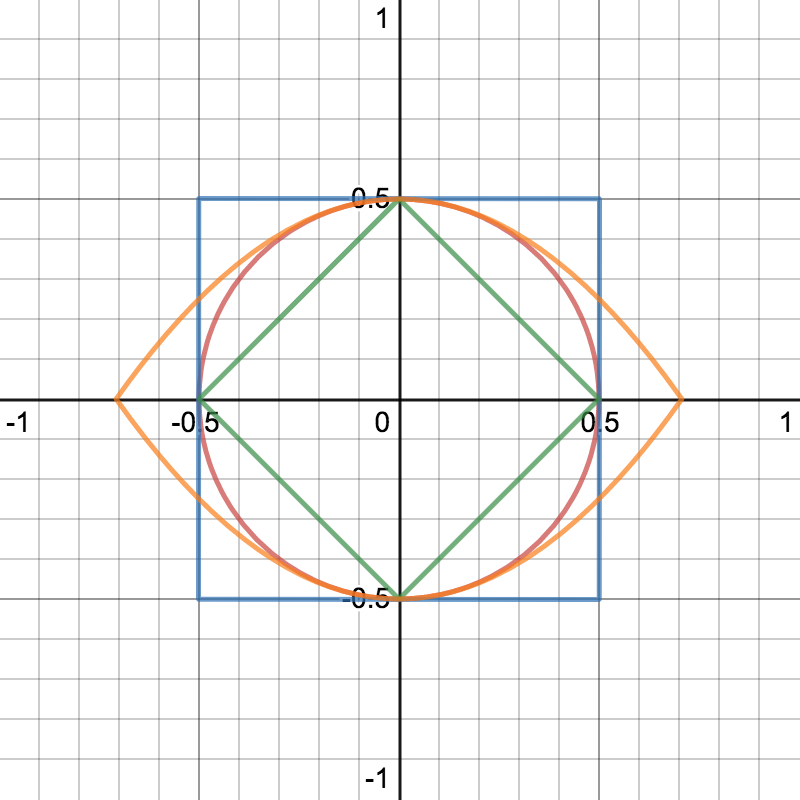
距離関数をグラフでみると
他にも色々と使われている
-
光の計算
-
内積
-
反射
-
階乗
-
指数
-
-
アニメーション
-
三角関数
-
回転行列
-
-
法線の算出
-
微分
-
-
その他
-
単位ベクトル
-
最小値
-
etc...
レイマーチングは
数学の塊
実に面白い
Section.5
素敵な作品たち
阿部悠希
Mathmare
・unity での制作
・様々な曲線による弾幕
aadebdeb
POOL
・WebGL
・Boids
・ジェネラティブアート
SeiichiSega
SHIBUYA scan
・Houdini
・スキャンされた渋谷の 3Dモデルの座標データ
soma-arc
Morph
・GLSL
・フラクタル

なめらかサンショウウオ
Web Graphic Experiments
・WebGL
・さまざまなノイズ

tokyomax
VFX Graph + RealSence
・Unity + VFX Graph
・RealSence
・ボリュメトリック
ビデオ
Simon Thommes
My Nodevember 2019
・Blender
・Shader Editor

Lusion
CineShader
・WebGL
・3D空間での
シェーダアート
・シェーダの取り込み
・立体にできる

かねた
Unity HDRP + Raymarching
・Unity
・HDPR
・レイマーチング
・リピテーション
・フラクタル

FMS_Cat
Until
・64KB WebGL Intro
・レイマーチング
・音もシェーダ
iq
Happy Jumping
・GLSL
・レイマーチング

まだまだ紹介したいが
あまりにも時間が足りない
のでまたの機会に
これからの活躍
Section.6
現在でもさまざまな分野で活躍している
クリエイティブコーディングですが
一度目線を変えて未来について
考えてみようと思います
CESって
知ってますか?
コンシューマー
エレクトロニクス
ショー
毎年1月にひらかれる
電子機器の見本市
その中で発表されたものに
焦点をあててみます
-
North Focals
-
Vuzix Blade
-
Realmax Qian
-
0glasses RealX
-
LetinAR
-
Magig Leap
-
nreal light
これらは
AR/MRグラス
スマートグラス
です
どんどん増えてきている
他にも
-
スマートミラー
-
木目調のディスプレイ
-
フレキシブルディスプレイ
-
視線認識型ライトフィールディスプレイ
-
シースルーディスプレイ
-
ホログラム
さまざまなディスプレイなどが増えて
プロトタイプや
既に製品化されているものも多い
つまり
あらゆるモノで
あらゆる空間で
表現できるように
なっていく
最後に
もうひとつ
スマートシティって
知ってますか?
MaaS
(モビリティ・アズ・ア・サービス)
の
終着点
先進的技術による
街の機能の最適化
トヨタが発表した実験都市
「ウーブン・シティ」
が話題になりました
表現の場が
広がりそうです
それもあるが
求められる表現の幅が
広がりそう
日常に溶け込む
静かな表現
イベントなどで街全体をつかった
壮大な表現
などなど
ということで
クリエイティブコーディングの
未来は希望に満ちている
THANKS

数学と表現 〜クリエイティブコーディングの世界〜
By Syuji Higa
数学と表現 〜クリエイティブコーディングの世界〜
- 400



















