Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

Thomas Cohn, Mark Petersen, Max Simchowitz, Russ Tedrake

Motion Planning Today
- Sampling-based planning
-
+
Global (probabilistic) completeness -
-
"Curse of Dimensionality" -
-
Non-smooth paths
-
- Trajectory optimization
-
-
Nonconvex -
+
Scales with dimension -
+
Smooth paths, dynamics
-
Motion Planning, Wikipedia


Motion Planning Today
- Sampling-based planning
-
+
Global(probabilistic)completeness -
-
"Curse of Dimensionality" -
-
Non-smooth paths
-
- Trajectory optimization
-
-
Nonconvex -
+
Scales with dimension -
+
Smooth paths, dynamics
-
Common challenge: collision avoidance
Motion Planning, Wikipedia


- Sampling-based planning
-
+
Global (probabilistic) completeness -
-
"Curse of Dimensionality" -
-
Non-smooth paths
-
- Trajectory optimization
-
-
Nonconvex -
+
Scales with dimension -
+
Smooth paths, dynamics
-
Planning through Convex Sets
Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.
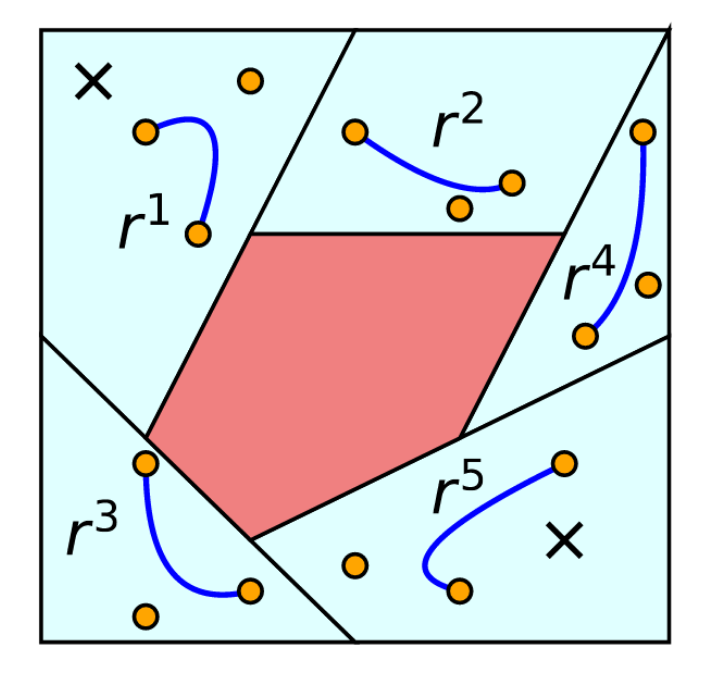
Obstacle avoidance: nonconvex
Safe-set containment: convex
Obstacle avoidance guarantees!
- Piecewise-linear trajectories: just check endpoints
- Bezier curves: check control points



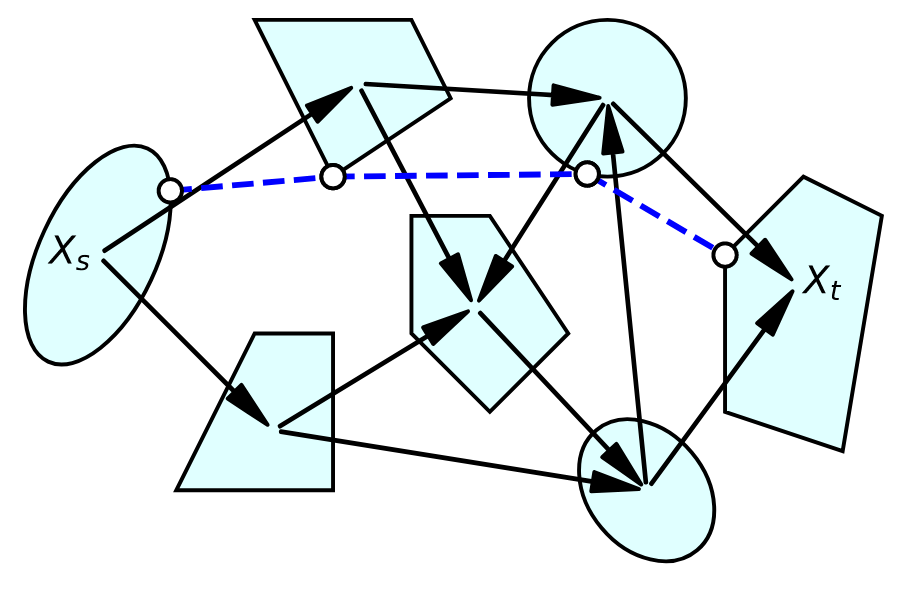
Motion Planning with GCS
- Represent C-Free with convex sets
- Formulate shortest path problem as MICP
- Can solve to optimality (branch and bound)
- In practice, relax and round yields a good result
Shortest Paths in Graphs of Convex Sets, Marcucci et. al.
Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.
What about non-Euclidean configuration spaces?
Configuration Space as a Manifold
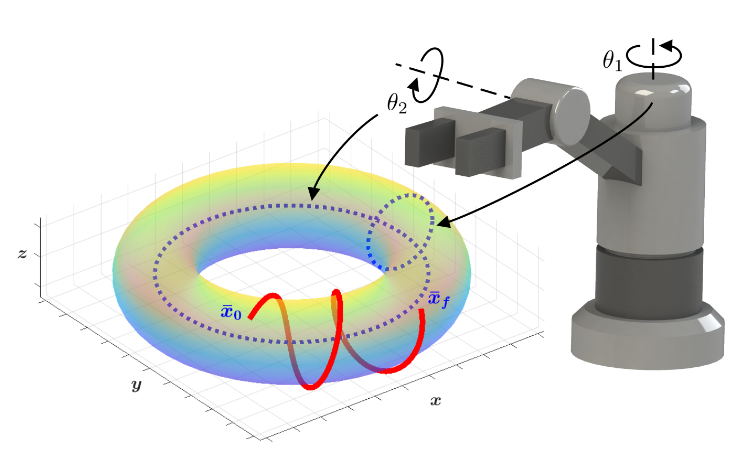
Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.
Configuration Space as a Manifold

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.

\(\mathcal{Q}\)
Configuration Space as a Manifold

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.

\(\mathcal{Q}\)
\(\overline{\mathcal{M}}\subseteq\mathcal{Q}\)
(Collision free subset)
Shortest-Path Planning along a Manifold

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.
\[\begin{array}{rl} \argmin & L(\gamma)\\ \textrm{subject to} & \gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\overline{\mathcal{M}})\\ & \gamma(0)=p\\ & \gamma(1)=q\end{array}\]
Shortest-Path Planning along a Manifold
\[\begin{array}{rl} \argmin & L(\gamma)\\ \textrm{subject to} & \gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\bar{\mathcal{M}})\\ & \gamma(0)=p\\ & \gamma(1)=q\end{array}\]
Minimize arc length
Path must be
piecewise-differentiable
Start at point \(p\)
Finish at point \(q\)
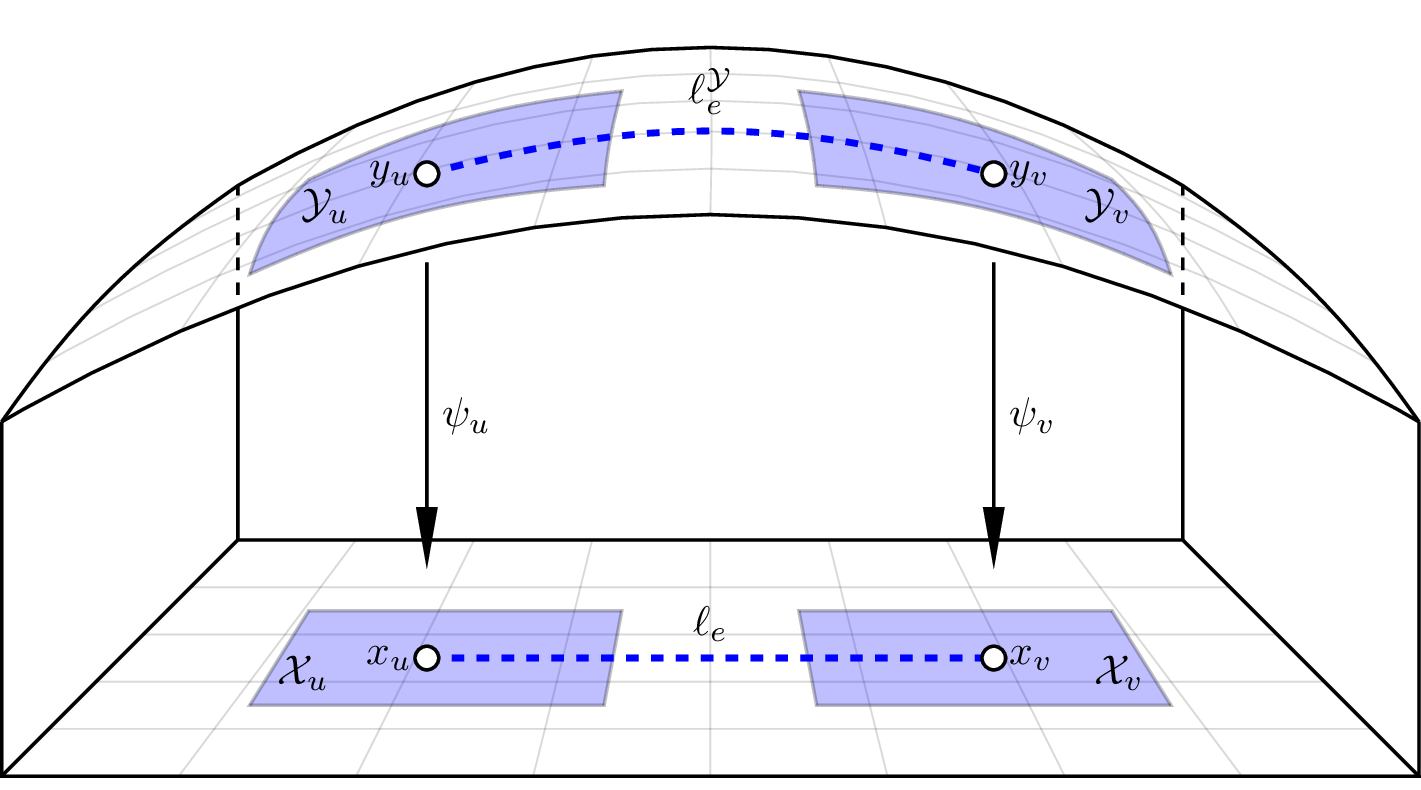
Computing Shortest Paths
- Formulate GCS on a Manifold
- Transform Problem back into Euclidean Space
- Additional requirements to ensure convexity


Results: PR2 Whole-Body Plans

Robot Operating System (ROS), Picknik
Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

Thomas Cohn, Mark Petersen, Max Simchowitz, Russ Tedrake

GGCS RSS Talk
By tcohn
GGCS RSS Talk
- 213



