Algorithms complexity
Telerik Academy Alpha
DSA
Table of contents
Algorithm complexity
Algorithm analysis
- Why we should analyze algorithms?
- Predict the resources the algorithm requires
- Computational time (CPU consumption)
- Memory space (RAM consumption)
- Communication bandwidth consumption
- The running time of an algorithm is:
- The total number of primitive operations executed (machine independent steps)
- Also known as algorithm complexity
- Predict the resources the algorithm requires
Algorithmic complexity
- What to measure?
- CPU Time
- Memory
- Number of steps
- Number of particular operations
- Number of disk operations
- Number of network packets
- Asymptotic complexity
Time Complexity
-
Worst-case
- An upper bound on the running time for any input of given size
-
Average-case
- Assume all inputs of a given size are equally likely
-
Best-case
- The lower bound on the running time (the optimal case)
Time Complexity - example
- Sequential search in a list of size n
- Worst-case:
- n comparisons
- Best-case:
- 1 comparison
- Average-case:
- n/2 comparisons
- Worst-case:
- The algorithm runs in linear time
- Linear number of operations
Algorithms Complexity
- Algorithm complexity is a rough estimation of the number of steps performed by given computation depending on the size of the input data
- Measured through asymptotic notation
- O(g) where g is a function of the input data size
- Examples:
- Linear complexity O(n) – all elements are processed once (or constant number of times)
- Quadratic complexity O(n^2) – each of the elements is processed n times
- Measured through asymptotic notation
Asymptotic Notation
- Asymptotic upper bound
- O-notation (Big O notation)
- For given function g(n), we denote by O(g(n)) the set of functions that are different than g(n) by a constant
\( O(g(n)) \) = {\( f(n) \): there exist positive constants \( c \) and \( n_0 \) such that \( f(n) \leq c*g(n) \) for all \( n \geq n_0 \) }
3*n^2 + n/2 + 12 \in O(n^2)
3∗n2+n/2+12∈O(n2)
3*n*log_2(3*n+1)+2*n-1 \in O(n*log n)
3∗n∗log2(3∗n+1)+2∗n−1∈O(n∗logn)
Typical Complexities
| Complexity | Notation | Description |
|---|---|---|
| constant | O(1) | Constant number of operations, not depending on the input data size, e.g. n = 1 000 000 → 1-2 operations |
| logarithmic | O(log n) | Number of operations proportional of log2(n) where n is the size of the input data, e.g. n = 1 000 000 000 → 30 operations |
| linear | O(n) | Number of operations proportional to the input data size, e.g. n = 10 000 → 5 000 operations |
| quadratic | O(n^2) | Number of operations proportional to the square of the size of the input data, e.g. n = 500→ 250 000 operations |
| cubic | O(n^3) | Number of operations proportional to the cube of the size of the input data, e.g. n = 200 → 8 000 000 operations |
| exponential | O(2^n) O(k^n) O(n!) |
Exponential number of operations, fast growing, e.g. n = 20 → 1 048 576 operations |
Time Complexity and Speed
| Complexity | 10 | 20 | 50 | 100 | 1000 | 10000 | 100000 |
|---|---|---|---|---|---|---|---|
| O(1) | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s |
| O(log n) | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s |
| O(n) | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s |
| O(n*logn) | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s | < 1s |
| O(n^2) | < 1s | < 1s | < 1s | < 1s | < 1s | 2s | 3-4 min |
| O(n^3) | < 1s | < 1s | < 1s | < 1s | 20 s | 5 hours | 231 days |
| O(2^n) | < 1s | < 1s | 26 days | hangs | hangs | hangs | hangs |
| O(n!) | < 1s | hangs | hangs | hangs | hangs | hangs | hangs |
| O(n^n) | hangs | hangs | hangs | hangs | hangs | hangs | hangs |
Time and Memory Complexity
- Complexity can be expressed as formula on multiple variables, e.g.
- Algorithm filling a matrix of size [n x m] with the natural numbers 1, 2, … will run in O(n*m)
- A traversal of graph with n vertices and m edges will run in O(n+m)
- Memory consumption should also be considered, for example:
- Running time O(n) & memory requirement O(n^2)
- n = 50 000 → OutOfMemoryException
The Hidden Constant
- Sometimes a linear algorithm could be slower than quadratic algorithm
- The hidden constant could be significant
- Example:
- Algorithm A makes: 100*n steps → O(n)
- Algorithm B makes: n*n/2 steps → O(n2)
- For n < 200 the algorithm B is faster
- Real-world example:
- Insertion sort is faster than quicksort for n <= 16
Polynomial Algorithms
- A polynomial-time algorithm is one whose worst-case time complexity is bounded above by a polynomial function of its input size \( W(n) \in O(p(n)) \)
- Examples:
- Polynomial-time:
- \( log(n) \)
- \( n^2 \)
- \( 3n^3+ 4n \)
- \( 2 * n*log(n) \)
- Non polynomial-time: \( 2^n, 3^n, k^n, n! \)
- Non-polynomial algorithms hang for large input data sets
- Polynomial-time:
Computational Classes
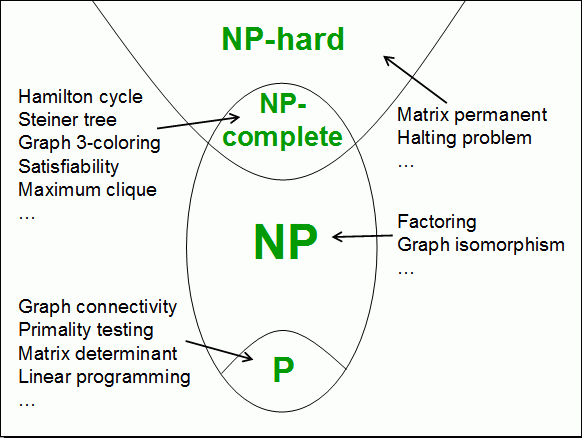
Complexity examples
Examples
- Runs in O(n) where n is the size of the array
The number of elementary steps is ~n
int FindMaxElement(int[] array)
{
int max = array[0];
for (int i = 0; i < array.Length; i++)
{
if (array[i] > max)
{
max = array[i];
}
}
return max;
}Examples
- Runs in \( O(n^2) \) where n is the size of the array
The number of elementary steps is ~n*(n-1)/2
long FindInversions(int[] array)
{
long inversions = 0;
for (int i = 0; i < array.Length; i++)
for (int j = i + 1; j < array.Length; i++)
if (array[i] > array[j])
inversions++;
return inversions;
}Examples
- Runs in cubic time \( O(n^3) \)
The number of elementary steps is ~\( n^3 \)
decimal Sum3(int n)
{
decimal sum = 0;
for (int a = 0; a < n; a++)
for (int b = 0; b < n; b++)
for (int c = 0; c < n; c++)
sum += a * b * c;
return sum;
}Examples
- Runs in quadratic time \( O(n*m) \)
The number of elementary steps is ~\( n*m \)
long SumMN(int n, int m)
{
long sum = 0;
for (int x = 0; x < n; x++)
for (int y = 0; y < m; y++)
sum += x * y;
return sum;
}Examples
- Runs in quadratic time \( O(n*m) \)
The number of elementary steps is ~\( n*m + min(m,n)*n \)
long SumMN(int n, int m)
{
long sum = 0;
for (int x = 0; x < n; x++)
for (int y = 0; y < m; y++)
if (x == y)
for (int i = 0; i < n; i++)
sum += i * x * y;
return sum;
}Examples
- Runs in exponential time \( O(2^n) \)
The number of elementary steps is ~\(2^n \)
decimal Calculation(int n)
{
decimal result = 0;
for (int i = 0; i < (1 << n); i++)
result += i;
return result;
}Examples
- Runs in linear time \( O(n) \)
The number of elementary steps is ~\(n \)
decimal Factorial(int n)
{
if (n == 0)
return 1;
else
return n * Factorial(n-1);
}Examples
- Runs in exponential time \( O(2^n) \)
The number of elementary steps is ~\( Fib(n+1) \) where ~\( Fib(k) \) is the `k`-th Fibonacci's number
decimal Fibonacci(int n)
{
if (n == 0)
return 1;
else if (n == 1)
return 1;
else
return Fibonacci(n-1) + Fibonacci(n-2);
}Questions?
[C# DSA] Algorithms complexity
By telerikacademy
[C# DSA] Algorithms complexity
- 1,501



