Graph Algorithms
Telerik Academy Alpha

 

DSA

 Table of contents

Graphs Traversal

Algorithms

 Graph Traversal Algorithms 

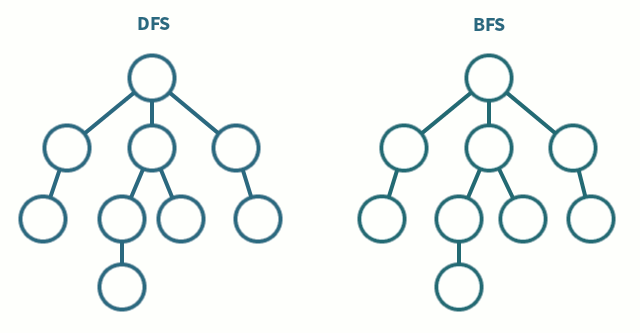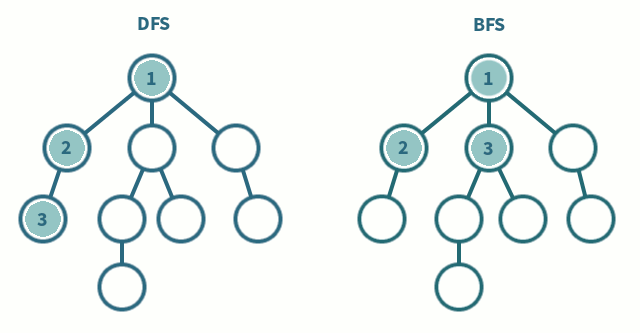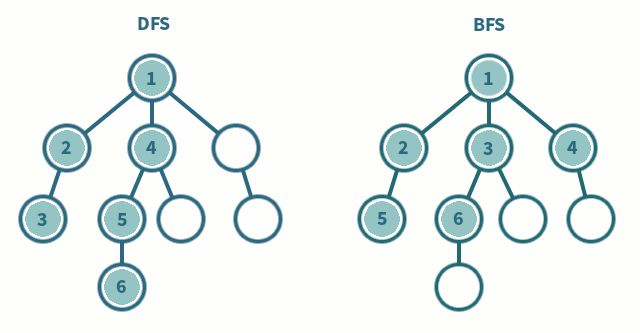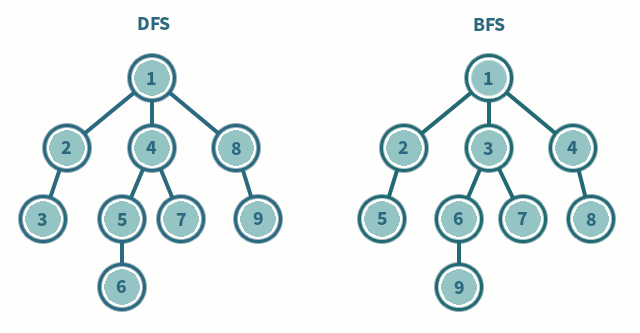
  • Depth-First Search (DFS) and Breadth-First Search (BFS) can traverse graphs
    • Each vertex should be visited at most once
BFS(node)
{
  queue ← node
  visited[node] = true
  while queue not empty
    v ← queue
    print v
    for each child c of v
      if not visited[c]
        queue ← c
        visited[c] = true
}
DFS(node)
{
  stack ← node
  visited[node] = true
  while stack not empty
    v ← stack
    print v
    for each child c of v
      if not visited[c]
        stack ← c
        visited[c] = true
}

 Recursive DFS Graph Traversal 

void TraverseDFSRecursive(node)
{
  if (not visited[node])
  {
    visited[node] = true;
    print node;
    foreach child node c of node
    {
       TraverseDFSRecursive(c);
    }
  }
}

void Main()
{
  TraverseDFS(firstNode);
}

Connectivity

 Connectivity

  • Connected component of undirected graph
    • A sub-graph in which any two nodes are connected to each other by paths

 Connectivity

  • A simple way to find number of connected components
    • A loop through all nodes and start a DFS or BFS traversing from any unvisited node
  • Each time you start a new traversing
    • You find a new connected component!
foreach node from graph G
{
  if node is unvisited
  {
    DFS(node);
    countOfComponents++;
  }
}

 Connectivity

  • Connected graph
    • A graph with only one connected component
  • Checking whether a graph is connected
    • If DFS / BFS passes through all vertices → graph is connected!

Topological Sorting

 Topological sorting

  • Topological sorting is just sorting a directed graph that has no cycles.

    • So you move through the nodes of the graph till you get to the end

    • Then on your way back from the recursion, you push them into the stack.

    • Because of the way the stack orders things (reverses the order), you’ll always get the first node, then the second, and so on all the way to the last

 Topological sorting

  • Topological sorting of a directed graph
    • Linear ordering of its vertices
    • For every directed edge (U, V), U comes before V in the ordering
  • Example:
    • 7, 5, 3, 11, 8, 2, 9, 10
    • 3, 5, 7, 8, 11, 2, 9, 10
    • 5, 7, 3, 8, 11, 10, 9, 2

 Topological sorting rules

  • Sorting is not unique
  • Undirected graph cannot be sorted
  • Directed graphs with cycles cannot be sorted
  • Various sorting algorithms exists and they give different results

 Topological sorting

  • Source removal algorithm
    • Create an Empty List
    • Find a Node without incoming Edges
    • Add this Node to the end of the List
    • Remove the Edge from the Graph
    • Repeat until the Graph is empty

 Topological sorting

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges

while S is non-empty do
    remove a node n from S
    insert n into L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S

if graph has edges then
    return error (graph has at least one cycle)
else
    return L (a topologically sorted order)

Topological sort demo

Dijkstra's Algorithm

 Dijkstra's Algorithm

  • We maintain two sets, one set contains vertices included in shortest path tree, other set includes vertices not yet included in shortest path tree. At every step of the algorithm, we find a vertex which is in the other set (set of not yet included) and has minimum distance from source.
    • Complexity
      • \( O((|V| + |E|).log(|V|)) \)
  • Applications – GPS, Networks, Air travels, etc.

 Dijkstra's Algorithm

  • Find the shortest path from vertex A to all other vertices
    • The path is a directed path between them such that no other path has a lower weight.
  • Assumptions
    • Edges can be directed or not
    • Weight does not have to be distance
    • Weights are positive or zero
    • Shortest path is not necessary unique
    • Not all edges need to be reachable

 Dijkstra's Algorithm

  • In non-weighted graphs or edges with same weight finding shortest path can be done with BFS
  • Note: Path from A to B does not matter - triangle inequiality

 Dijkstra's Algorithm

  • In weighted graphs – simple solution can be done with breaking the edges in sub-vertexes
  • Note: Too much memory usage even for smaller graphs!

 Dijkstra's Algorithm

  • Solution to this problem:
    • Priority queue instead of queue
    • Keeping information about the shortest distance so far
  • Steps:
    • Enqueue all distances from S
    • Get the lowest in priority - B
    • If edge (B, A) exists, check (S, B) + (B, A) and save the lower one
    • Overcome the triangle inequality miss

 Dijkstra's Algorithm

  1. Set the distance to every node to Infinity except the Source 
  2. Mark every node as unprocessed
  3. Choose the first unprocessed node with smallest non-infinity distance as current. If there is none, the algorithm has finished
  4. At first we set the current node our Source
  5. Calculate the distance for all unprocessed neighbors by adding the current distance to the already calculated one
  6. Set a new value if the new distance is smaller 
  7. Mark the current node as processed
  8. Repeat step 3.

 Dijkstra's Algorithm

set all nodes DIST = INFINITY;
set current node the source and distance = 0;
Q -> all nodes from graph, ordered by distance;
while (Q is not empty)
    a = dequeue the smallest element (first in PriorityQueue);
    if (distance of a == INFINITY) break

    foreach neighbour v of a     
        potDistance = distance of a + distance of (a-v)      
        if (potDistance < distance of v)
            distance of v = potDistance;
            reorder Q;

Dijkstra's Algorithm Demo

Questions?

[C# DSA] Graph Algorithms

By telerikacademy

Made with Slides.com

[C# DSA] Graph Algorithms

  • 1,481

More from telerikacademy