Pigeonhole Principle

Thameera Senanayaka

Allion Technologies

aka Why lossless compression is not guaranteed

Task: Fill each square with a 1 or a -1 so that each row, column and diagonal has a different sum

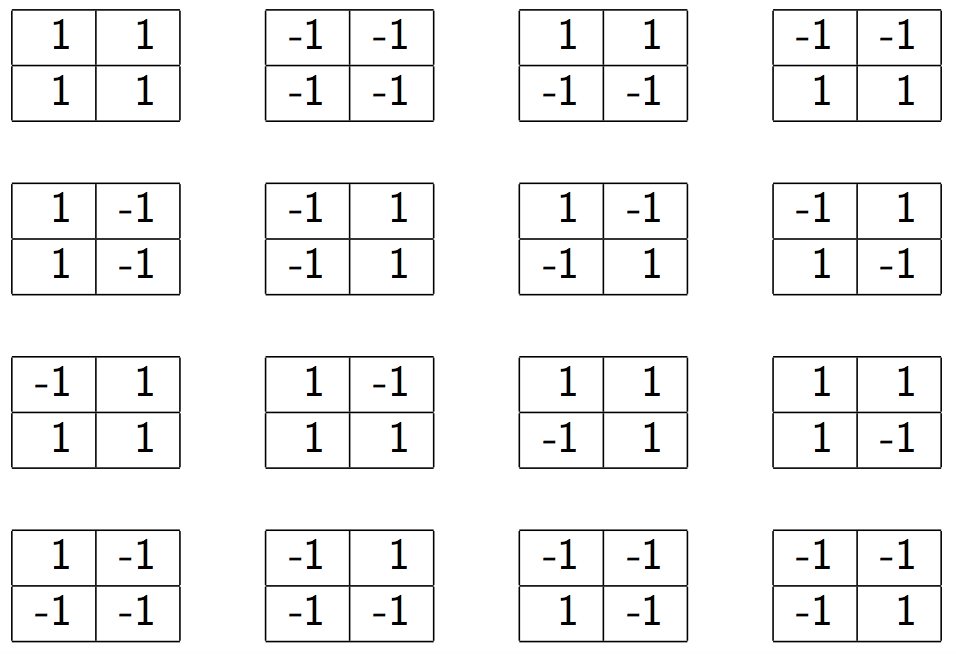
Number of sums needed:

2 rows + 2 columns + 2 diagonals = 6

Maximum sum:

1 + 1 = 2

Minimum sum:

-1 + -1 = -2

Number of possible sums:

-2 to 2 = 5

# of sums needed < # of sums possible

Pigeonhole principle

If you have n pigeonholes and n+1 pigeons, then there's one (or more) pigeonhole with at least two pigeons.

There are at least two people in Allion Technologies with the same birthday date

35 people

31 possible dates

There are red and blue socks bag.

How many socks do you need to take out so you will get a matching pair?

There are 100 people at a party.

They shake hands with each other.

Some people might not shake hands.

Show that there are at least two people who shook the same number of hands.

Show that there's a multiple of 2015 that is entirely consisted of 1s and 0s in its decimal representation.

111

11...11

(2016 1's)

2016 numbers.

Two of them have same remainder.

2015 possible remainders when divided by 2015.

x - y = divides by 2015

x -y has only 1's and 0's

Why can't we guarantee lossless compression for all possible inputs?

Question: If the compression algorithm makes some inputs smaller, then should it make some other inputs larger?

Thank you!