Quasi-resonant collisions in kinetic theory and bi-temperature systems
38e séminaire de mécanique des fluides numérique
CEA-SMAI/GAMNI
IHP, January 27, 2026
\(\phantom{x}^*\)post-doc at CERMICS, École des Nationale des Ponts et Chaussées
\text{T. Borsoni}^*, \text{ L. Boudin, J. Mathiaud, F. Salvarani}
a peculiar polyatomic Boltzmann model
Microscopic
Macroscopic
Kinetic theory: statistical description of gases
Mesoscopic
gaz large collection of molecules
Part 1. Standard polyatomic Boltzmann
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
Outline
- How to model quasi-resonance
- Peculiar characteristic of the dynamic
- Numerical experiments
Part 1. Standard polyatomic Boltzmann
x
+
+
polyatomic molecules have an internal structure
v
?
x
+
v
x
position, velocity
position, velocity, angular velocity, vibration modes,...
monoatomic
polyatomic
Internal state
\textcolor{orange}{?} : (\omega,n_1,n_2,n_3)
Internal
energy quantile
Internal
energy level
\textcolor{olive}{?} : I =\frac12\mathcal{J}|\omega|^2 + E_1 n_1 + E_2 n_2 + E_3n_3
x,v
x,v, \textcolor{orange}{?}
How to describe the internal structure?
[Borgnakke\(\text{--}\)Larsen 75', Desvillettes 97']
[Wang-Chang\(\text{--}\)Uhlenbeck 51', Waldmann 57', Snider 60']
[Taxman 58', B.\(\text{--}\)Bisi\(\text{--}\)Groppi '23]
\omega
n_1
n_2
n_3
I \in \R_+
q \in \R_+
(\partial_t + v \cdot \nabla_x) f_{t,x}(v,I) = Q(f_{t,x})(v,I)
- We study \(f \equiv f_{t,x}(v, I)\) density of molecules
+
x
the polyatomic Boltzmann equation
(with internal energy levels description)
v
Boltzmann equation:
I
energy of the molecule
= \frac12|v|^2 + I
- Description of a gaz as a collection of molecules
Each molecule either moves in straight line of collides with another molecule
\partial_t f_{t}(v,I) = Q(f_{t})(v,I)
- We study \(f \equiv f_{t}(v, I)\) density of molecules
the space homogeneous
polyatomic Boltzmann equation
(with internal energy levels description)
v
Space homogeneous Boltzmann equation
I
energy of the molecule
= \frac12|v|^2 + I
- Assume that the gaz is homogeneous in space
Dynamic driven by collisions between molecules
v \cdot \nabla_x
the collision operator \(Q\)
v
v,I
v_*,I_*
v',I'
v'_*,I'_*
\begin{align*}
v+v_*&=v'+v'_* \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &= \frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_* \\
\end{align*}
Conservation laws
I
(momentum)
(total energy)
energy of the molecule
= \frac12|v|^2 + I
\newcommand{\dd}{\mathrm{d}}
Q(f)(v,I) = \int
[f(v',I') f(v'_*,I'_*) -
f(v,I) f(v_*,I_*)] \;
\textcolor{purple}{B(v,v_*,v',v'_*,I,I_*, I',I'_*)}
\(\textcolor{purple}{B(v,v_*,v',v'_*,I,I_*, I',I'_*)} > 0 \iff \) the collision is possible
Collision kernel
\partial_t f_{t}(v,I) = Q(f_{t})(v,I),
Entropy and equilibrium
Boltzmann entropy functional
\mathcal{M}(v,I) = \textcolor{blue}{\rho}\, Z(\textcolor{blue}{T})^{-1} \, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T}} - \frac{I}{\textcolor{blue}{T}} \right)
\newcommand{\dd}{\mathrm{d}}
H (f) := \int f \log f
Boltzmann's H-theorem
(i) 2\(^{nd}\) principle of thermodynamics
(ii) Equilibrium
If
then
\displaystyle \frac{\mathrm{d} H(f_t)}{\mathrm{d} t} =: -D(f_t) \leqslant 0.
entropy dissipation functional
For any
g \equiv g(v,I),
D(g) = 0 \quad \iff \quad g = \mathcal{M}
With \(\mathcal{M}\) the Maxwellian (Gibbs) distribution
\(\textcolor{blue}{\rho}\) average density
\(\textcolor{blue}{u}\) bulk velocity
\(\textcolor{blue}{T}\) temperature
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
quasi-resonant collisions
v,I
v_*,I_*
v',I'
v'_*,I'_*
(separation kinetic/internal)
Observed experimentally, e.g. \(\mathrm{CO}_2\)
v,I
v_*,I_*
v',I'
v'_*,I'_*
I+I_* \approx I' + I'_*.
\begin{align*}
v+v_*&=v'+v'_*, \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*,
\end{align*}
quasi-resonant possible collisions
How to make it rigorous?
(almost separation kinetic/internal)
resonant possible collisions
I+I_* = I' + I'_*.
\begin{align*}
v+v_*&=v'+v'_*, \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*,
\end{align*}
standard possible collisions
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
How to model quasi-resonance?
Other contributions :
- Aoki-Bernhoff (2025)
- Graille-Magin-Massot (2012)
- Frozen collisions of Torrilhon and Pavic
quasi-resonant collisions by truncation of the kernel
Set of possible collisions \(\equiv\) support of the collision kernel
resonant possible collisions
v,I
v_*,I_*
v',I'
v'_*,I'_*
I+I_* = I' + I'_*.
\begin{align*}
v+v_*&=v'+v'_*, \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*,
\end{align*}
B^{\rm \textcolor{grey}{std}}
Let
a standard collision kernel
\mathrm{supp}(B^{\rm \textcolor{grey}{std}})
standard possible collisions
\mathrm{supp}(B^{\rm {res}})
``B^{\textcolor{green}{\text{res}}} = B^{\rm \textcolor{grey}{std}} \times \textcolor{green}{\delta_{I+I_* = I'+I'_*}}"
quasi-resonant collisions by truncation of the kernel
Set of possible collisions \(\equiv\) support of the collision kernel
quasi-resonant possible collisions
v,I
v_*,I_*
v',I'
v'_*,I'_*
I+I_* \approx_\varepsilon I' + I'_*.
\begin{align*}
v+v_*&=v'+v'_*, \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*,
\end{align*}
B^{\rm \textcolor{grey}{std}}
Let
a standard collision kernel
\mathrm{supp}(B^{\rm \textcolor{grey}{std}})
\varepsilon
B^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}} = B^{\rm \textcolor{grey}{std}} \times
\textcolor{red}{\frac{c \,\mathbf{ \bm{1}_{\mathcal{V}_{\varepsilon}}}}{\textcolor{red}{\varepsilon}}}
\textcolor{black}{\forall} \varepsilon \textcolor{black}{> 0,}
\(\mathcal{V}_{\varepsilon}\)
\mathrm{supp}(B^{\text{\textcolor{red}{q-res}}}_{\textcolor{red}{\varepsilon}})
Family of collision kernels:
truncation family
the truncation family
B^{\rm \textcolor{grey}{std}}
a standard collision kernel
B^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}} = B^{\rm \textcolor{grey}{std}} \times
\textcolor{red}{\frac{c \,\mathbf{ \bm{1}_{\mathcal{V}_{\varepsilon}}}}{\textcolor{red}{\varepsilon}}}
\textcolor{black}{\forall} \varepsilon \textcolor{black}{> 0,}
\(\mathcal{V}_{\varepsilon}\)
The collision is in \(\textcolor{red}{\mathcal{V}_{\varepsilon}}\) if
\left| \eta(R) - \eta(R') \right| \leqslant \textcolor{red}{\varepsilon}
- Pre-and post-collision energy ratios:
\in [0,1]
- A diffeomorphism \(\eta : (0,1) \to \R\)
Remark:
R = R'
\iff
the collision is resonant
The collision is in \(\textcolor{green}{\mathcal{V}_{0}}\) iff
\(\mathcal{V}_{0}\)
R' =
R =
pre-collision kinetic energy
total energy
post-collision kinetic energy
total energy
the truncation family
B^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}} = B^{\rm \textcolor{grey}{std}} \times
\textcolor{red}{\frac{c \,\mathbf{ \bm{1}_{\mathcal{V}_{\varepsilon}}}}{\textcolor{red}{\varepsilon}}}
\textcolor{black}{\forall} \varepsilon \textcolor{black}{> 0,}
\(\mathcal{V}_{\varepsilon}\)
The collision is in \(\textcolor{red}{\mathcal{V}_{\varepsilon}}\) if
\left| \log \frac{\frac{R}{R'}}{\frac{1-R}{1-R'}} \right| \leqslant \textcolor{red}{\varepsilon}
- Pre-and post-collision energy ratios:
R' =
R =
\in [0,1]
pre-collision kinetic energy
total energy
- Take \(\eta : R \in (0,1) \mapsto \log \frac{R}{1-R}\)
In practice:
controls a ratio of ratios of ratios!
B^{\rm \textcolor{grey}{std}}
a standard collision kernel
Remark:
R = R'
\iff
the collision is resonant
The collision is in \(\textcolor{green}{\mathcal{V}_{0}}\) iff
post-collision kinetic energy
total energy
\newcommand{\dd}{\mathrm{d}}
Q^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}}(f)(v,I) = \int
\big[ f(v',I') f(v'_*,I'_*) - f(v,I) f(v_*,I_*) \big] \times
B^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}}(v,v_*,v',v'_*,I,I_*,I',I'_*)
Family of collision kernels:
Family of collision operators:
\textcolor{black}{\forall} \varepsilon \textcolor{black}{> 0,}
The quasi-resonant Boltzmann dynamics
B^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}} = B^{\rm \textcolor{grey}{std}} \times
\textcolor{red}{\frac{c \,\mathbf{ \bm{1}_{\mathcal{V}_{\varepsilon}}}}{\textcolor{red}{\varepsilon}}},
\textcolor{black}{\forall} \varepsilon \textcolor{black}{> 0,}
Family of quasi-resonant Boltzmann dynamics
\textcolor{black}{\forall} \varepsilon \textcolor{black}{> 0,}
\partial_t f^{\textcolor{red}{\varepsilon}}_{t} = Q_{\textcolor{red}{\varepsilon}}^{\textcolor{red}{\text{q-res}}}(f^{\textcolor{red}{\varepsilon}}_{t})
RESONANT ASYMPTOTICS \(\varepsilon \to 0\)
Resonant asymptotics
Q^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}}(f) \underset{\textcolor{red}{\varepsilon} \to 0}{\longrightarrow}
Q^{\rm \textcolor{green}{res}} (f),
``B^{\textcolor{green}{\text{res}}} = B^{\rm \textcolor{grey}{std}} \times \textcolor{green}{\delta_{I+I_* = I'+I'_*}}"
B^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}} = B^{\rm \textcolor{grey}{std}} \times
\textcolor{red}{\frac{c \,\mathbf{ \bm{1}_{\mathcal{V}_{\varepsilon}}}}{\textcolor{red}{\varepsilon}}},
\textcolor{black}{\forall} \varepsilon \textcolor{black}{> 0,}
we expect the quasi-resonant dynamic to be "close" to the resonant one
\newcommand{\dd}{\mathrm{d}}
Q^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}}(f)(v,I) = \int
\big[ f(v',I') f(v'_*,I'_*) - f(v,I) f(v_*,I_*) \big] \times
B^{\textcolor{red}{\text{q-res}}}_{\textcolor{red}{\varepsilon}}(v,v_*,v',v'_*,I,I_*,I',I'_*)
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
Peculiar characteristic of the dynamic
Resonant and Quasi-resonant long-time properties
and consequent expected behaviour
\mathcal{M}_2(v,I) \propto\, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T_k}} - \frac{I}{\textcolor{blue}{T_i}} \right)
Equilibrium:
two distinct temperatures
kinetic
temperature
internal
temperature
\mathcal{M}(v,I) \propto\, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T}} - \frac{I}{\textcolor{blue}{T}} \right)
Equilibrium:
two distinct temperatures
same
temperature
one single temperature
\partial_t f^{\textcolor{red}{\varepsilon}}_{t} = Q_{\textcolor{red}{\varepsilon}}^{\textcolor{red}{\text{q-res}}}(f^{\textcolor{red}{\varepsilon}}_{t})
\partial_t f^{\textcolor{green}{0}}_{t} = Q^{\textcolor{green}{\text{res}}}(f^{\textcolor{green}{0}}_{t})
For the resonant dynamic
For the quasi-resonant dynamic
Boudin-Rossi-Salvarani 2022
time
\(\mathcal{O}(1)\) short time
\(\mathcal{O}(\textcolor{red}{\varepsilon}^{-2})\) long time
relaxation towards a
two-temperature
Maxwellian
\propto \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T_k}} - \frac{I}{\textcolor{blue}{T_i}} \right)
- the solution (almost) remains of two-temperature Mawellian shape
- the kinetic (\(\textcolor{blue}{T_k}\)) and internal (\(\textcolor{blue}{T_i}\)) temperatures relax towards each other
(1)
(2)
Expected behaviour of the quasi-resonant dynamics 1/2
\partial_t f^{\textcolor{red}{\varepsilon}}_{t} = Q_{\textcolor{red}{\varepsilon}}^{\textcolor{red}{\text{q-res}}}(f^{\textcolor{red}{\varepsilon}}_{t})
If \(\varepsilon \ll 1\), we expect
Explicit ODE system on the two temperatures?
Explicit Landau-Teller ODE system
\partial_t f^{\textcolor{red}{\varepsilon}}_{t} = Q_{\textcolor{red}{\varepsilon}}^{\textcolor{red}{\text{q-res}}}(f^{\textcolor{red}{\varepsilon}}_{t})
Proposition.
If
with
f^{\textcolor{red}{\varepsilon}}_{t=0} = \mathcal{M}_2 \propto \exp\left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T^0_k}} - \frac{I}{\textcolor{blue}{T^0_i}} \right),
\displaystyle\frac{\mathrm{d} T_i(t)}{\mathrm{d} t}_{|t=0} = \varepsilon^2 \, \alpha(T_i^0, T_k^0) \; (T_k^0 - T_i^0) + o(\varepsilon^2)
then for a certain family of kernels \(B^{\textcolor{grey}{std}}\) and energy laws \(\varphi\), we have
with \(\alpha\) explicit.
Internal temperature at time \(t\):
T_i(t) \leftrightarrow \iint_{\R^3 \times \R_+} \, I \, f_t^{\textcolor{red}{\varepsilon}}(v,I) \, \mathrm{d} v \, \varphi(I)\, \mathrm{d} I
(T_i(t), \, T_k(t)) \approx (\overline{T}_i(t), \, \overline{T}_k(t))
\newcommand{\dd}{\mathrm{d}}
\newcommand{\e}{\textcolor{red}{\varepsilon}}
\begin{equation*}
\begin{cases}
&\overline{T}_k'(t) = \e^2 \, \alpha[\overline{T}_k, \overline{T}_i] (\overline{T}_i - \overline{T}_k),\\
&\overline{T}_i'(t) = \e^2 \; \widetilde{\alpha}[\overline{T}_k, \overline{T}_i] (\overline{T}_k - \overline{T}_i),
\end{cases} \quad {\small(\overline{T}_i(0),\overline{T}_k(0)) = (T_i(0),T_k(0))}.
\end{equation*}
(LT)
(2)
Long-time behaviour: Landau-Teller relaxation of (\(\textcolor{blue}{T_k}\)) and (\(\textcolor{blue}{T_i}\)) towards each other
expected behaviour of the QUASI-RESONANT dynamics 2/2
let's check this numerically!
time
\(\mathcal{O}(1)\) short time
\(\mathcal{O}(\textcolor{red}{\varepsilon}^{-2})\) long time
relaxation towards a
two-temperature
Maxwellian
\propto \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T_k}} - \frac{I}{\textcolor{blue}{T_i}} \right)
- the solution (almost) remains of two-temperature Mawellian shape
- the kinetic (\(\textcolor{blue}{T_k}\)) and internal (\(\textcolor{blue}{T_i}\)) temperatures relax towards each other
(1)
(2)
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
Numerical experiment
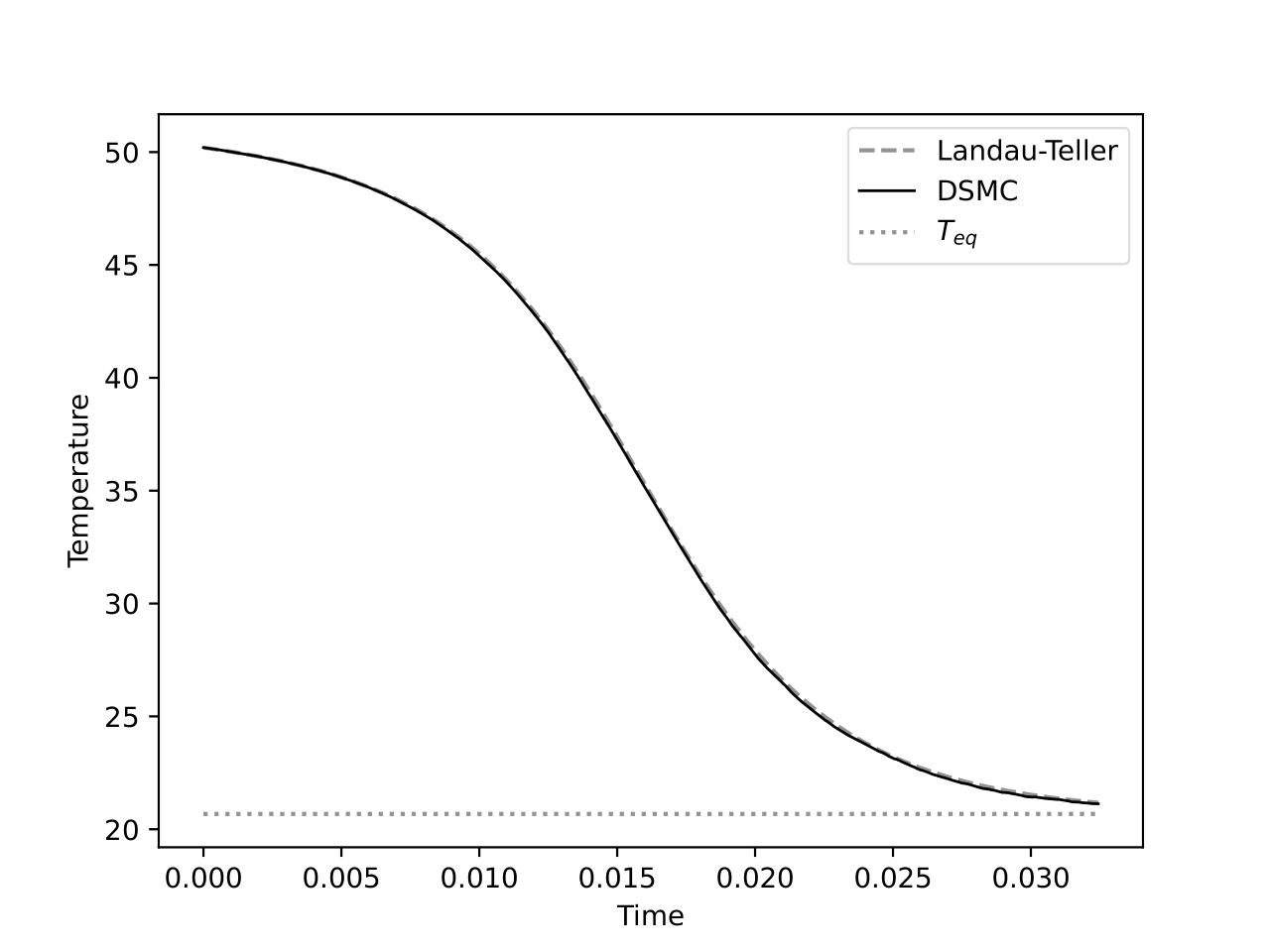
Numerical experiment
\bullet \; T_k^0 = 1, \quad T_i^0 = 50, \quad T_{eq} = 20.6,
(T_i(t), \, T_k(t)) \approx (\overline{T}_i(t), \, \overline{T}_k(t))
Parameters
\varepsilon = 10^{-1},
\varphi(I) = 1,
\textcolor{black}{\bullet \; B^{\text{q-res}}_\varepsilon(v,v_*,\sigma,I,I_*,I',I'_*) = \frac{\mathbf{1}_{[I'+I'_* \leqslant E]}}{2 \pi}
\times \frac{E^3}{E_i \, E_i' \, \sqrt{E_k}} \times }
\frac{\mathbf{1}_{[|\log(E_k/E_i) - \log(E_k' / E_i')| \leqslant \varepsilon]}}{\varepsilon}\textcolor{black}{,}
E_k = \frac14|v-v_*|^2, \quad E_i = I+I_*, \quad E_k' = \frac14|v'-v'_*|^2, \quad E'_i = I'+I'_*, \quad E = E_k + E_i = E_k'+ E_i'.
N_{\mathrm{DSMC}} = 10^5.
- Simulation of the quasi-resonant Boltzmann equation with DSMC
\partial_t f^{\textcolor{red}{\varepsilon}}_{t} = Q_{\textcolor{red}{\varepsilon}}^{\textcolor{red}{\text{q-res}}}(f^{\textcolor{red}{\varepsilon}}_{t})
(T_i(t), \, T_k(t)) \approx (\overline{T}_i(t), \, \overline{T}_k(t))
T_i(t)
- Integration of the LT ODE system
\newcommand{\dd}{\mathrm{d}}
\newcommand{\e}{\textcolor{red}{\varepsilon}}
\begin{equation*}
\begin{cases}
&\overline{T}_k'(t) = \e^2 \, \alpha[\overline{T}_k, \overline{T}_i] (\overline{T}_i - \overline{T}_k),\\
&\overline{T}_i'(t) = \e^2 \; \widetilde{\alpha}[\overline{T}_k, \overline{T}_i] (\overline{T}_k - \overline{T}_i),
\end{cases}
\end{equation*}
\overline{T}_i(t)
\overline{T}_i(t)
T_i(t)
Numerical experiment
Goal. Check if
(T_i(t), \, T_k(t)) \approx (\overline{T}_i(t), \, \overline{T}_k(t))
temperatures associated with the quasi-resonant Boltzmann dynamics
temperatures of the Landau-Teller ODE system
Simulation of the quasi-resonant Boltzmann equation with DSMC
- \(N\) numerical particles, each with velocity \(v\) and energy quantile \(q\)
- at each time step, randomly select couples of particles to collide, according to the collision kernel
- for each collision, randomly draw the new states of the particles, according to the collision kernel
Conclusion
- The shape of the distribution is known at all times (two-temperature Maxwellian)
For the quasi-resonant Boltzmann dynamic
- The two temperatures are related to a Landau-Teller ODE system
- This ODE system is explicit from the Boltzmann model in some cases
Thank you for your attention!
Presentation IHP
By Thomas Borsoni
