关于红包
一些你以为你知道但是其实或许你不知道的故事但也许你应该知道的故事

红包系统
也不像它看起来那么简单
- 高并发
- 瞬时大流量
- 单SKU队列
- 财务审计
微博的红包服务架构

红包生成
- 维护公平感
- 制造惊喜感
- 预算控制
也不像它看起来那么简单
100块钱发100个红包
公平感
每个红包应当多少钱?
E(X) = { \sum X \over n }
E(X)=n∑X
100块钱发100个红包
惊喜感
你希望拿多少钱?
D(X) \to N ( N \ggg 1)
D(X)→N(N⋙1)
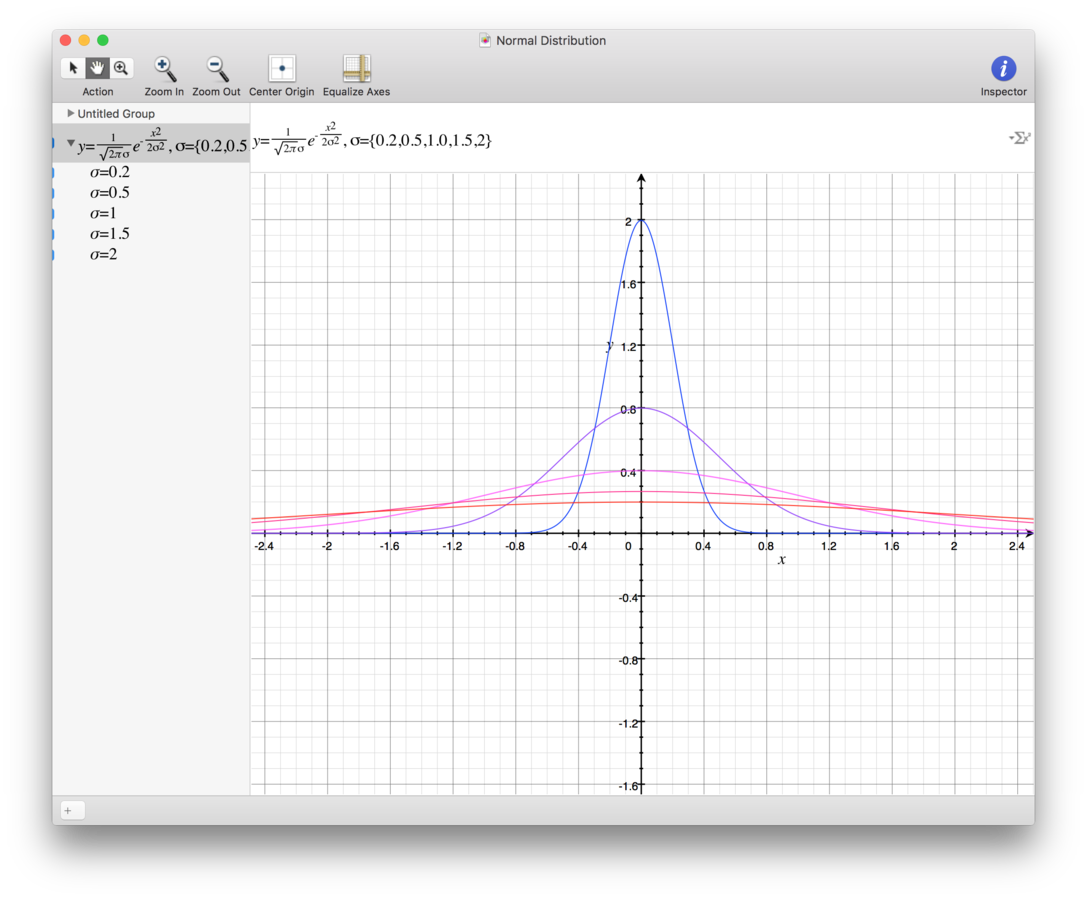
发100个红包平均1元的红包
预算控制
预算需要是100元整
D(\sum X) = 0
D(∑X)=0
E(\sum X) = E(\sum X)
E(∑X)=E(∑X)
需求弄明白了
怎么实现呢?
function generateValue(max) {
return Math.random() * max;
}分析一下
function generateValue(max) {
return Math.random() * max;
}max = 2 \cdot E(X)
max=2⋅E(X)
D(X) = { max \over 12}
D(X)=12max
= { E(X) \over 6 }
=6E(X)
\therefore E(\sum X) = \sum E(X)
∴E(∑X)=∑E(X)
\therefore D(\sum X) = \sum D(X)
∴D(∑X)=∑D(X)
= { N \cdot E(X) \over 6 }
=6N⋅E(X)
E(X) = { max \over 2 }
E(X)=2max
问题来了
E(X) = { max \over 2 }
E(X)=2max
D(X) = { max \over 12}
D(X)=12max
E(\sum X) = { max \cdot N \over 2 }
E(∑X)=2max⋅N
D(\sum X) = { N \cdot max \over 12 }
D(∑X)=12N⋅max
D(\sum X) = 0
D(∑X)=0
E(\sum X) = \sum E(X)
E(∑X)=∑E(X)
E(X) = { \sum X \over n }
E(X)=n∑X
D(X) \to N ( N \ggg 1)
D(X)→N(N⋙1)
需求
结论
Experiment
const maxValue = 100
const totalTimes = 1000
const distribution = {}
const recordSum = (value) => {
const count = distribution[value] || 0
distribution[value] = count + 1
}
const random = () => Math.random() * maxValue >> 0
const doOnce = () => compose(recordSum, sum, times)(random, totalTimes)
times(doOnce, 10000)
toPairs(distribution).forEach((arr) => console.log(`${arr[0]}, ${arr[1]}`))E(X) = { max \over 2 } = 50
E(X)=2max=50
D(X) = { max \over 12} \approx 8.33
D(X)=12max≈8.33
E(\sum X) = { max \cdot N \over 2 } = 50000
E(∑X)=2max⋅N=50000
D(\sum X) = { N \cdot max \over 12 } \approx 8333.33
D(∑X)=12N⋅max≈8333.33
Result
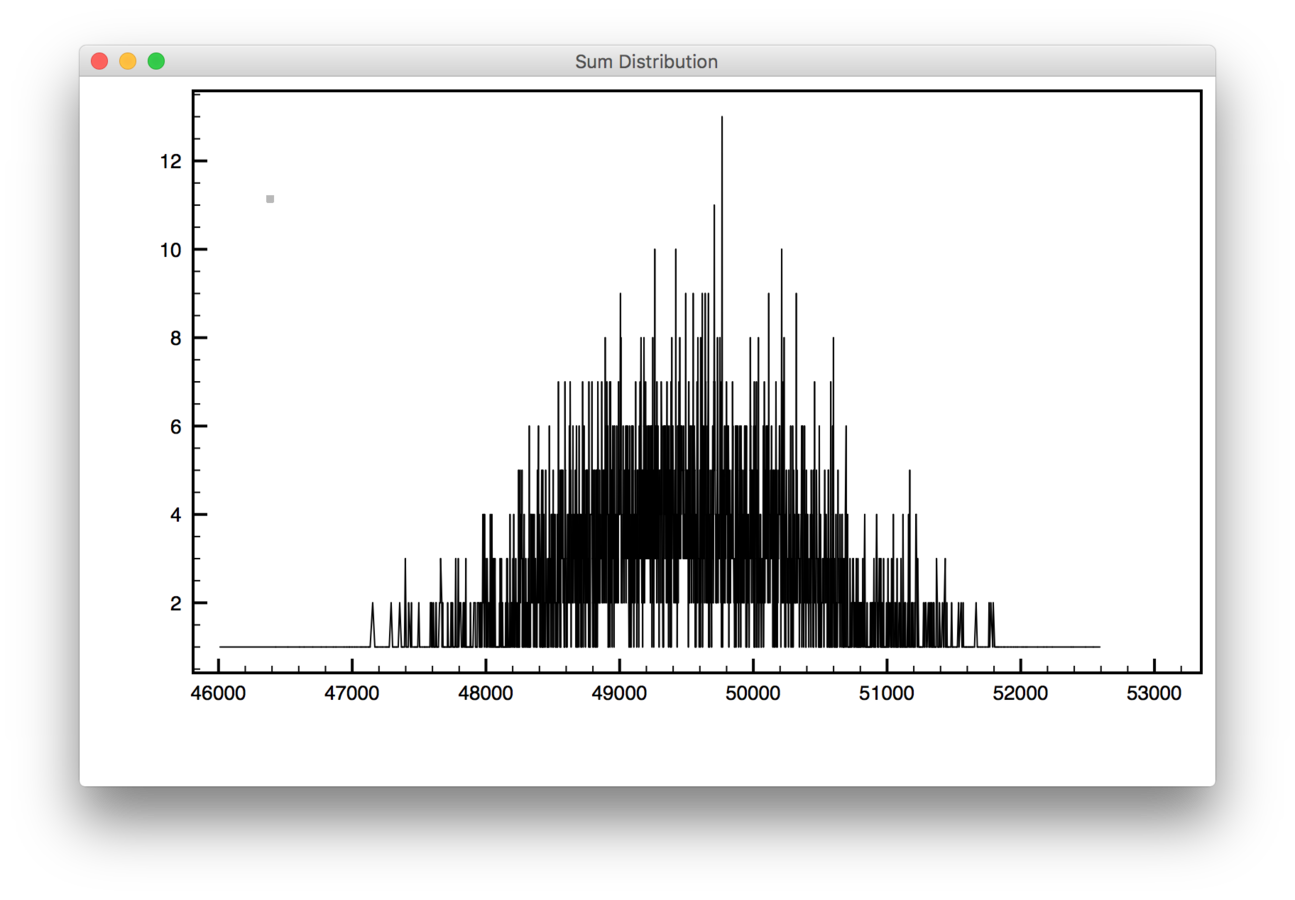
E(\sum X) = { max \cdot N \over 2 } = 50000
E(∑X)=2max⋅N=50000
D(\sum X) = { N \cdot max \over 12 } \approx 8333.33
D(∑X)=12N⋅max≈8333.33
微信怎么做的?
public static double getRandomMoney(LeftMoneyPackage _leftMoneyPackage) {
// remainSize 剩余的红包数量
// remainMoney 剩余的钱
if (_leftMoneyPackage.remainSize == 1) {
_leftMoneyPackage.remainSize;
return (double) Math.round(_leftMoneyPackage.remainMoney * 100) / 100;
}
Random r = new Random();
double min = 0.01;
double max = _leftMoneyPackage.remainMoney / _leftMoneyPackage.remainSize * 2;
double money = r.nextDouble() * max;
money = money <= min ? min : money;
money = Math.floor(money * 100) / 100;
_leftMoneyPackage.remainSize--;
_leftMoneyPackage.remainMoney -= money;
return money;
}金额分布
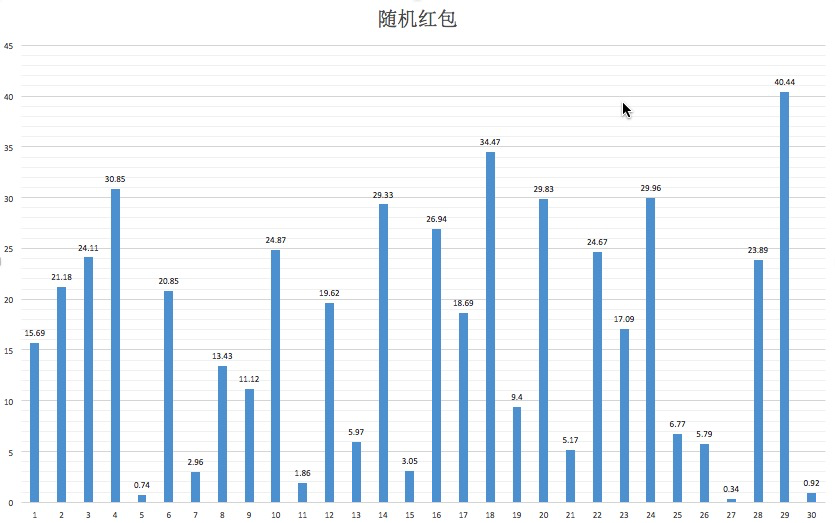
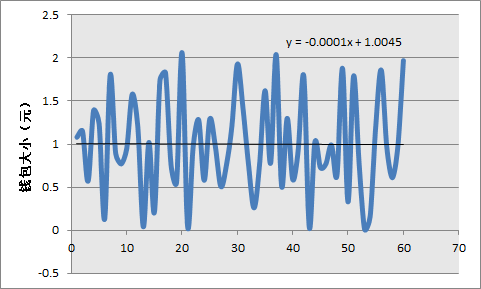
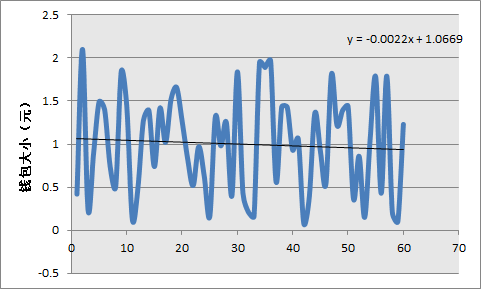
2000次后的金额分布
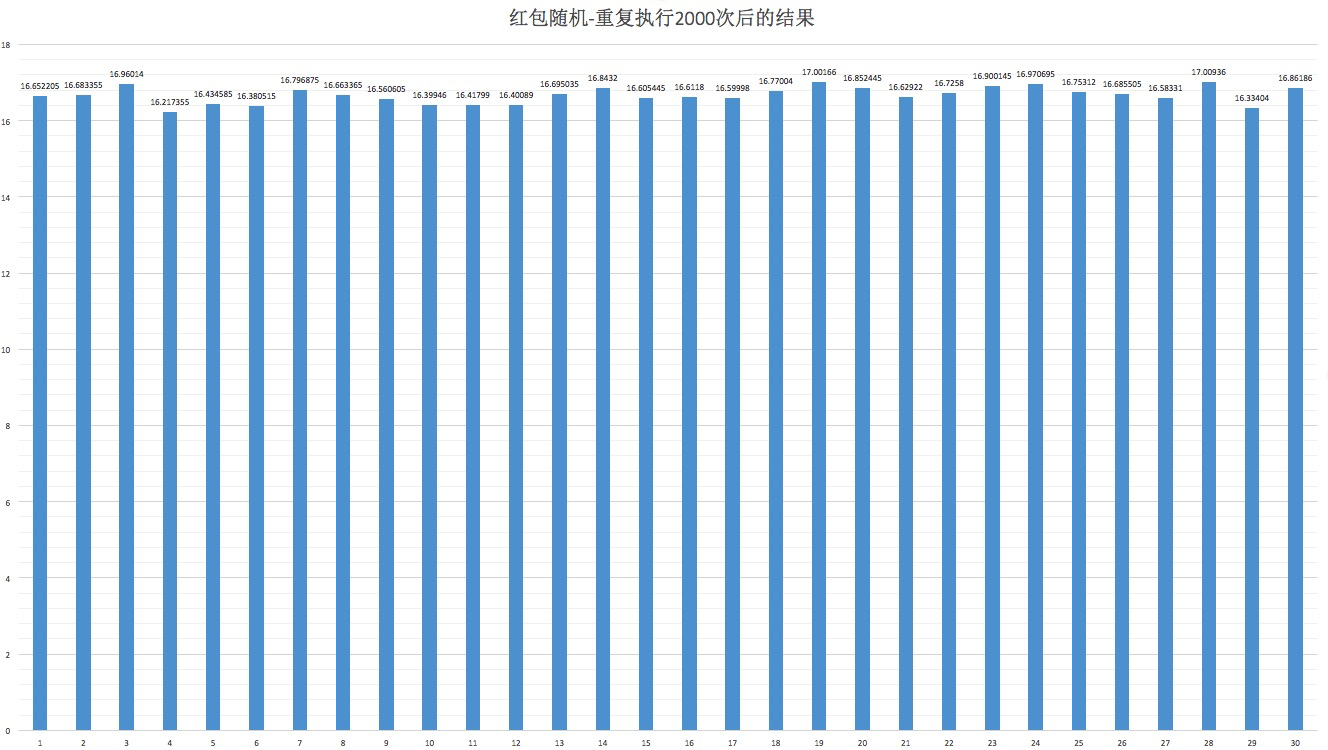
60元60份的结果
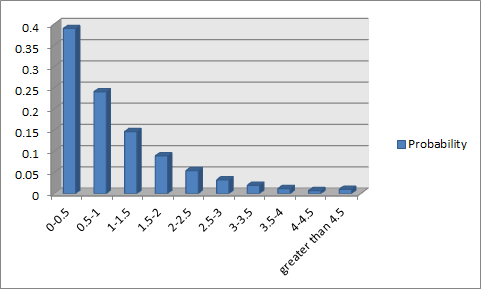
自适应的分布
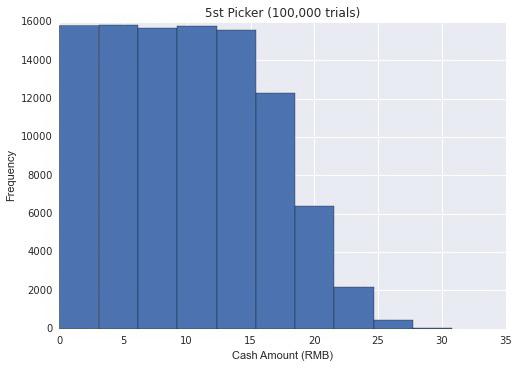
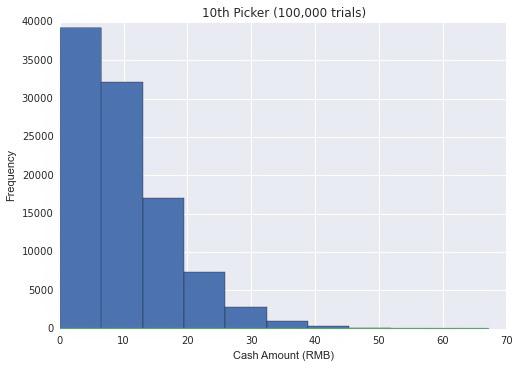
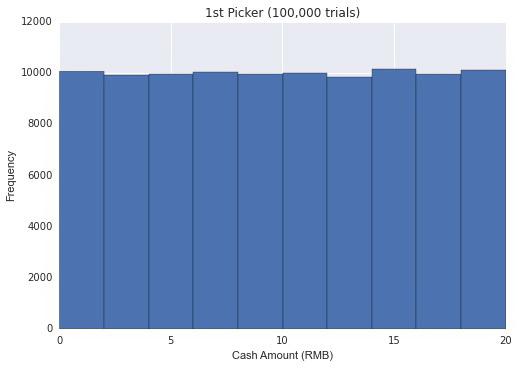
不影响公平性
THANKS
Q&A
关于红包
By timnew
关于红包
- 532



