Minimum Spanning Tree
by jacky860226
Undirected Weighted Graph
- A undirected graph whose edges have weights.
Definition
1
2
3
4
- Example:
- \(V=\{1,2,3,4\}\)
- \(E=\{\)
\((1,3), (1,2),\)
\((2,3), (4,2),\)
\((3,4)\)
\(\}\) - \(W\left(\left(1,2\right)\right)=13\)
2
8
13
7
6
$$G=(V,E)$$
- \(V\) is a set of vertices of \(G\) and \(E\) is a set of edges of \(G\).
- \(\forall e \in E\),
we define the weight function \(W(e)\) is the weight of \(e\).
Spanning Tree
- Give graph \(G=(V,E)\)
-
Spanning Tree is a connected tree \(T=(V,E')\) where
$$E' \subseteq E$$
2
4
3
2
1
8
13
7
6
Minimum Spanning Tree(MST)
- Give graph \(G=(V,E)\)
-
Minimum Spanning Tree is a Spanning Tree which
the sum of edge weights is minimum.
2
6
7
13
8
4
3
2
1
Greedy Algorithms to find MST
- Kruskal's algorithm
- Prim's algorithm
- Borůvka's algorithm
- ...
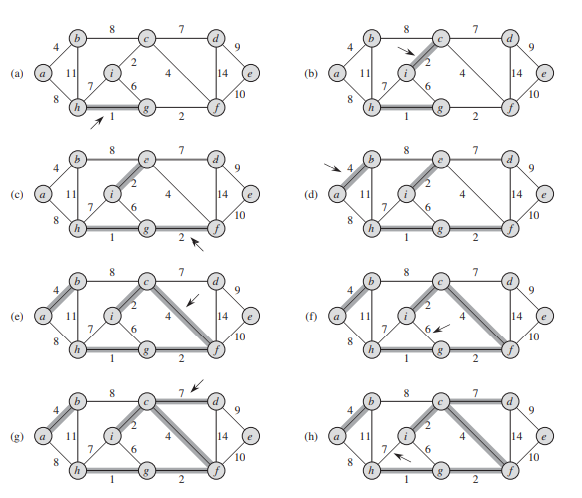
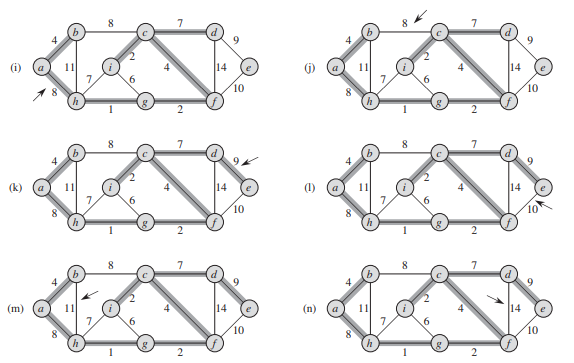
Kruskal's algorithm
- Input \(G=(V,E)\)
- Let \(E_s = E, E' = \{\}\)
- while ( \(E_s\) is not empty)
- Remove an edge \(e\) with minimum weight from \(E_s\)
- If add \(e\) into \(E'\) will not create a circle
- Add \(e\) into \(E'\)
- If \(T=(V,E')\) is a tree
- output \(T\) is a minimum spanning tree
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Complexity
- Sort the edges by weight
- Using Union Find Set to maintain trees
#include <tuple>
#include <vector>
#include <algorithm>
#include <numeric> // for iota(first, last, val) setting iterator value
using namespace std;
struct DSU // disjoint set no rank-comp-merge
{
vector<int> fa;
DSU(int n) : fa(n) { iota(fa.begin(), fa.end(), 0); } // auto fill fa from 0 to n-1
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) { fa[find(x)] = find(y); }
};
int kruskal(int V, vector<tuple<int, int, int>> E) // save all edges into E, instead of saving graph via adjacency list
{
sort(E.begin(), E.end());
DSU dsu(V);
int mcnt = 0;
int ans = 0;
for (auto e : E)
{
int w, u, v; // w for weigth, u for start, v for destination
tie(w, u, v) = e;
if (dsu.find(u) == dsu.find(v))
continue;
dsu.merge(u, v);
ans += w;
if (++mcnt == V - 1)
break;
}
return ans;
}
CODE
How
to
Proof?
Edge inclusion lemma
$$G=(V,E)$$
- Let \(S\) be a subset of \(V\), and suppose \(e = (u, v)\) is the minimum cost edge of \(E\), with \(u\) in \(S\) and \(v\) in \(V-S\).
- Then \(e\) is in a certain minimum spanning tree of \(G\).
\(u\)
\(v\)
\(V-S\)
\(S\)
\(e\)
Proof
- Suppose \(T\) is a minimum spanning tree that does not contain \(e\).
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Proof
- Add \(e\) to \(T\), this creates a cycle.
- The cycle must have some edge \(e' = (u', v')\) with \(u'\) in \(S\) and \(v'\) in \(V-S\).
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Proof
- By definition, we have \(W(e) \le W(e')\)
- \(W(e) = W(e')\) because \(T\) is a minimum spanning tree.
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Proof
- By definition, we have \(W(e) \le W(e')\)
- \(W(e) = W(e')\) because \(T\) is a minimum spanning tree.
- We can remove \(e'\) and add \(e\) to create a new tree \(T'\)
- \(T'\) must be a minimum spanning tree!
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Prim's algorithm
- \(G=(V,E)\)
- Let \(S=\{v_0\}\) where \(v_0 \in V\)
- Let \(E'=\{\}\)
- while(\(V-S\) not empty)
- Let \(e = (u, v)\) is the minimum cost edge of \(E\), with \(u\) in \(S\) and \(v\) in \(V-S\)
- Add \(e\) into \(E'\)
- add \(v\) into \(S\)
-
If \(T=(V,E')\) is a tree
- output \(T\) is a minimum spanning tree
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b,e\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b,e,c\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b,e,c,g\}\)
Complexity
- Using Binary heap maintain edges
- Using adjacency list
Complexity
- Using Fibonacci heap maintain edges
- Using adjacency list
#include <vector>
#include <queue>
#include <utility>
using namespace std;
#define enp pair<int, int> // pair<edge_val, node>
int prim_pq(vector<vector<enp>> E){
vector<bool> vis;
vis.resize(E.size(), false);
vis[0] = true;
priority_queue<enp, vector<enp>, greater<enp>> pq;
for(auto e: E[0]){
pq.emplace(e.first, e.second);
}
int ans = 0; // min value for MST
while(pq.size()){
int w, v; // edge-weight, vertex index
tie(w, v) = pq.top();
pq.pop();
if(vis[v])
continue;
vis[v] = true;
ans += w;
for(auto e: E[v]){
if(!vis[e.second])
pq.emplace(e.first, e.second);
}
}
return ans;
}
CODE
UVa 908
Tioj 1211
Minimum Bottleneck Path
-
\(G=(V,E)\)
-
For any path \(p\), we call a \(Bottleneck(p)\) is an edge \(e \in p\)
which \(W(e)\) is maximum -
A Minimum Bottleneck Path from \(u\) to \(v\)
is a path \(p\) from \(u\) to \(v\) which \(W(Bottleneck(p))\) is minimum
Minimum Bottleneck Path
4
8
7
9
11
8
6
15
9
7
5
e
c
f
g
b
d
a
Minimum Bottleneck Path
4
8
7
9
11
8
6
15
9
7
5
e
c
f
g
b
d
a
Minimum Bottleneck Lemma
- \(G=(V,E)\)
- Let \(T=(V,E')\) is a Minimum Spanning Tree of \(G\)
- \(\forall u,v \in V\):
- \(path(u,v)\) in \(T\) is a Minimum Bottleneck Path in \(G\)
Proof
We ignore proof because it is similar to
Edge Inclusion lemma
UVa 10369
UVa 1395
Minimum Spanning Tree by jacky860226
By tunchin kao
Minimum Spanning Tree by jacky860226
- 80



