Stack & Queue
Outline
- What is data structure
- stack
- Queue
- Link List
Intro. to Data Structure
Briefly Speaking : how to store data in a computer
Like a Library
Your book is data
And how to sort and store these books
Target : find a book a quick as possible
In real world

A new Book
Where to put this book?
An old book
Delete this book
Maybe need to check
In computer
Some Valuation
- Time Complexity
- Space Complexity
- Coding Complexity
Data Structure as tools
Solving a Problem
(multi) Data Structure + (multi) Algorithm
Common Operation on DS
push/insert : put in an element
pop/delete : take out an element
query : search, if-exist, quantitiy, max, min
Stack
stack (堆疊)
Properties
- First in last out (FILO)
- each pop operation, pop out the last one enter stack
- like plates

stack implementation
- Array
- Linked List ( mention latter )
What we need in array implementation ?
- Use a variable "top" to record the position of top
- top = -1 -> the stack is empty
- push : top increase 1
- pop : top decrease 1
| Outcome |
|---|
| Stack |
|---|
| Operation |
|---|
Stack
<- top
| Outcome |
|---|
| Stack |
|---|
| Operation |
|---|
| push 1 |
Stack
<- top
| Outcome |
|---|
| Stack |
|---|
| 1 |
| Operation |
|---|
| push 1 |
Stack
<- top
| Outcome |
|---|
| Stack |
|---|
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
Stack
<- top
| Outcome |
|---|
| Stack |
|---|
| 19 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
Stack
<- top
| Outcome |
|---|
| Stack |
|---|
| 19 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
Stack
<- top
| Outcome |
|---|
| Stack |
|---|
| 35 |
| 19 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
Stack
<- top
| Outcome |
|---|
| Stack |
|---|
| 35 |
| 19 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
Stack
<- top
| Outcome |
|---|
| 35 |
| Stack |
|---|
| 19 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
Stack
<- top
| Outcome |
|---|
| 35 |
| Stack |
|---|
| 19 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
Stack
<- top
| Outcome |
|---|
| 35 |
| 19 |
| Stack |
|---|
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
Stack
<- top
| Outcome |
|---|
| 35 |
| 19 |
| Stack |
|---|
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
| push 7 |
Stack
<- top
| Outcome |
|---|
| 35 |
| 19 |
| Stack |
|---|
| 7 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
| push 7 |
Stack
<- top
| Outcome |
|---|
| 35 |
| 19 |
| Stack |
|---|
| 7 |
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
| push 7 |
| pop |
Stack
<- top
| Outcome |
|---|
| 35 |
| 19 |
| 7 |
| Stack |
|---|
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
| push 7 |
| pop |
Stack
<- top
| Outcome |
|---|
| 35 |
| 19 |
| 7 |
| Stack |
|---|
| 1 |
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
| push 7 |
| pop |
| pop |
Stack
<- top
| Outcome |
|---|
| 35 |
| 19 |
| 7 |
| 1 |
| Stack |
|---|
| Operation |
|---|
| push 1 |
| push 19 |
| push 35 |
| pop |
| pop |
| push 7 |
| pop |
| pop |
Stack
<- top
Use Array
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
push 4
top = -1
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 4 |
top = 0
push 7
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 4 | 7 |
top = 1
Use Array
pop, outcome = 7
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 4 |
top = 0
push 17, push 39
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 4 | 17 | 39 |
top = 2
push 25, pop, pop, push 14 pop
What are the outcomes , top, and remaining value in array ?
STL : standard template library
#include <stack>
std::stack<int> steak;
steak.push(10);
steak.push(18);
std::cout << steak.top() << '\n';
// return the top value of stack. No pop out.
steak.pop();
// only pop out the top one of stack, no return;
std::cout << steak.top() << '\n';
Please share your screen
Homework
Use stack
Queue
(佇列)
Queue Properties
- first in first out (FIFO)
- like lining up
- pop operation : pop out the oldest element in queue
- some structure : single direction, cycle linked list
Queue Operations
- push : put an element into queue
- pop : take an element out of queu
Queue Implementation
Same
- Array
- Linked list
Implement in array
- use a variable "front" to record the position in front of the first element.
- use a variable "rear" to record the position of the last element
- if front == rear -> queue is empty
- push : rear + 1
- pop : front + 1
| Outcome |
|---|
| Queue |
|---|
| Operation |
|---|
Queue
<- front = rear
| Outcome |
|---|
| Queue |
|---|
| Operation |
|---|
| push 'a' |
Queue
<- front = rear
| Outcome |
|---|
| Queue |
|---|
| a |
| Operation |
|---|
| push 'a' |
Queue
<- front
<- rear
| Outcome |
|---|
| Queue |
|---|
| a |
| Operation |
|---|
| push 'a' |
| push 't' |
Queue
<- front
<- rear
| Outcome |
|---|
| Queue |
|---|
| t |
| a |
| Operation |
|---|
| push 'a' |
| push 't' |
Queue
<- front
<- rear
| Outcome |
|---|
| Queue |
|---|
| t |
| a |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| Queue |
|---|
| t |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| Queue |
|---|
| t |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| Queue |
|---|
| e |
| t |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| Queue |
|---|
| e |
| t |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| Queue |
|---|
| k |
| e |
| t |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| Queue |
|---|
| k |
| e |
| t |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| t |
| Queue |
|---|
| k |
| e |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| t |
| Queue |
|---|
| k |
| e |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
| pop |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| t |
| e |
| Queue |
|---|
| k |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
| pop |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| t |
| e |
| Queue |
|---|
| k |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
| pop |
| pop |
Queue
<- front
<- rear
| Outcome |
|---|
| a |
| t |
| e |
| k |
| Queue |
|---|
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
| pop |
| pop |
Queue
<- front =rear
Now Stack is empty !!
| Outcome |
|---|
| a |
| t |
| e |
| k |
| Queue |
|---|
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
| pop |
| pop |
| push 'm' |
Queue
<- front =rear
Now Stack is empty !!
| Outcome |
|---|
| a |
| t |
| e |
| k |
| Queue |
|---|
| m |
| Operation |
|---|
| push 'a' |
| push 't' |
| pop |
| push 'e' |
| push 'k' |
| pop |
| pop |
| pop |
| push 'm' |
Queue
<- front
Now Stack is empty !!
<- rear
But array will running out ?
| 0 | 1 | ... | 21473646 | 21473657 |
|---|---|---|---|---|
| k |
^------------------------unused-----------^
front
rear
The problem : if an element is popped out,
that position can't be used anymore.
Solution 1
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| k | a | e |
front
rear
when rear is at the end, move(shift) all element to the begin.
pushing an 'r'
Solution 1
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| k | a | e | r |
front
rear
When rear is at the end, move(shift) all element to the begin.
shift then push an 'r'
Solution 2 : use circular queue
We just push then element as usual
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| r | k | a | e |
front
rear
pushing an 'r'
Solution 2 : use circular queue
What should be aware of ?
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| r | k | l | k | a | e |
front
rear
- When rear = front ? is it empty or full
Sacrifice a place and note that when
rear == front -> empty
rear == front -1 -> full
Some cheat
Actually, in some problem, the size of input is not so big.
We can just allocate an array that large enough.
Solution 3 : Linked List
Later we will mention
Time complexity
push |
pop |
|
|---|---|---|
stack |
O(1) |
O(1) |
queue |
O(1) |
O(1) |
#include <queue>
std::queue<int> que;
que.push(1);
std::cout << que.front() << '\n';
// return the value of first element
// (the next one to be pop),
// not performing pop
que.push(2);
std::cout << que.front() << '\n';
que.pop();
// pop out the firsst element, no return
std::cout << que.front() << '\n';What are the outputs ?
Homework UVa-540
Use linked list
Linked List
(鏈結串列)
Real life Question
There are N trains, each one has M carriages
Now you have some work to do
connect a-th train to b-th train
and the station master ask you how is the final train like


Real life Question
We just simply connect the train
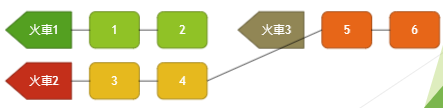
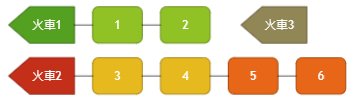
Now, how to implement in program ?
We try array
An 1D array represents a train
| 0 | 1 | 2 | 3 | 4 | ... | |
|---|---|---|---|---|---|---|
| train 1 | 1 | 3 | ||||
| train 2 | 5 | 7 | ||||
| train 3 | 9 | 11 |
How long should an array be ?
N trains, M carriages
Largest possible train is N*M
So your array should be N*M long...
Connect the train
| 0 | 1 | 2 | 3 | 4 | ... | |
|---|---|---|---|---|---|---|
| train 1 | 1 | 3 | ||||
| train 2 | 5 | 7 | 9 | 11 | ||
| train 3 |
for (int i = 0; i < len_b; i++){
train_a[len_a + i] = train_b[i];
}
len_a += len_b;Problems
- Waste lots of space
- Most of the space are empty
- Allocate N*M but only use M
- Waste of time
- Each operation needs O(N)
- Array is not good...
Linked List
Basic Elements
Node : (data + pointer) (like carriage)
link lots of nodes together
use a pointer "head" point to the first node
the last node point to null
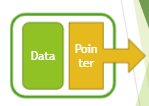

Properties of Linked List
- Every element only take care of its next element
- We only take care of the start (head)
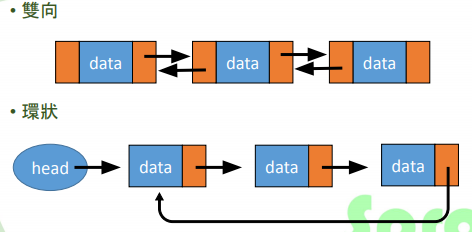
- Classification : single linked list, doubly, circular
- No random access
Operations of Linked List
- Insert : insert an element between two elements or at the head or at the end.
- Delete : delete an element
Implementation
- Define a struct / class "Node" as the node of linked list, contain data the pointer to the next node.
- At the outside we only save the head as the start point.
struct Node{
int _data;
Node * _next;
}
int main(){
Node* node = new Node();
}Pros of Linked List
- Better usage of memory
- insert and delete fast
- (record how to delete an element in array)
Insert
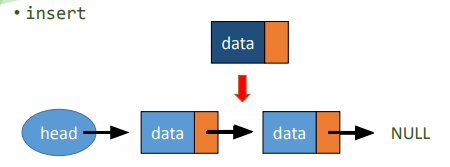
void insert(Node *A, Node* B){
A->_next = B;
}Delete
void delete(Node *A){
Node * tode = A->next;
A->next = A->next->next;
delete tode; // free memory
}
Is there some problem about the code ?
Delete
void delete(Node *A){
Node * tode = A->next;
if(A->next != nullptr){
A->next = A->next->next;
delete tode; // free memory
}else{
A->next = nullptr;
}
}
Stack & Queue
Use linked list implement stack
- push : insert a node in front of head
- pop : delete the node head point to
Use linked list implement queue
- push : insert a node at the end of last node
- pop : delete the node head point to
Implement Stack
class Stack{
private:
struct Node{
Node *_next;
int _data;
}
Node * head
public:
void push(int val){
Node * newNode = new Node(val);
newNode->next = head;
head = newNode;
}
void pop(int val){
Node * tode = head;
head = head->next;
delete head;
}
};Implement Queue
class Stack{
private:
struct Node{
Node *_next;
int _data;
}
Node * head;
Node * end;
public:
void push(int val){
Node * newNode = new Node(val);
end->next = newNode;
end = newNode;
}
void pop(int val){
Node * tode = head;
head = head->next;
delete head;
}
};Of course there are lots of implementing Detail need to be cover
Time Complexity
| random access | push front |
push back |
pop front |
pop back |
|
|---|---|---|---|---|---|
| Array | yes | O(n) | O(1) | O(n) | O(1) |
| Linked List | No | O(1) | O(1) | O(1) | O(1) |
Some classic Problems
give you a string of parentheses, determine if it is legal
"{([])([]{{}[]})}" => legal
"({([][]))} => illegal
Thinking 1
Count how many left parenthesis and right parenthesis ?
How about this ?
{ [ ( ] ) } ?
Thinking 2
Use stack !!
push in when encounter left one
pop out when match right
Problem 2
The maximum Rectangle in a Bar Graph
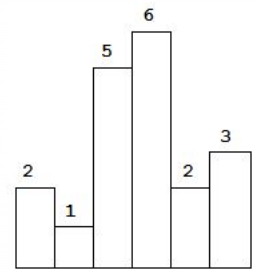
Challenge Problem 2
The maximum Rectangle in a Bar Graph

Try to implement Stack & Queue by yourself
And get AC of previous problems use your own stack & queue
Homework
Remember to send me the AC screen shot !
Problems tutorial
UVa 514- Rails
UVa 514- Rails
We stimulate the stack directly
And try to produce the order it wants
So
1. if the top is equal to the current wanting order, pop out
2. if the top is not equal, we can't pop.
So we put another new train into stack
Pseudo Code
up_coming = 1
push up_coming into stack
up_coming = up_coming + 1
want = 0
while up_coming <= N or stack isn't empty
if(order[want] equal to top of stack)
pop out stack
else
push up_coming into stack
up_coming = up_coming+1
How about the invalid case ?
If the order is valid
then all element in stack will eventually popped out due to matching.
If the order is invalid
eventually there must some place the stack start to unmatch
and never match again.
So in all element pushed into stack and still not matching
It must be invalid
Pseudo Code
up_coming = 1
push up_coming into stack
up_coming = up_coming + 1
want = 0
while up_coming <= N or stack isn't empty
if(order[want] equal to top of stack)
pop out stack
else
push up_coming into stack
up_coming = up_coming+1
if(up_coming == N+1 and the top of stack != order[want])
failed
break
UVa 540
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| a | x |
|---|
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| a | x | y |
|---|
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| a | b | x | y |
|---|
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| b | x | y |
|---|
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| b | x | y | r |
|---|
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| b | c | x | y | r |
|---|
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
We think as a group queue
| b | c |
|---|
| x | y |
|---|
| r |
|---|
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
We think as a group queue
| c |
|---|
| x | y |
|---|
| r |
|---|
when popping... pop the element from the top queue of group queue
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
We think as a group queue
| x | y |
|---|
| r |
|---|
when popping... pop the element from the top queue of group queue
when popping... pop the top queue of group queue
if the top queue is empty
UVa 540
Here is the assumption
If two person who both in the same group is in the queue, the must be contiguous.
| groups |
|---|
| a, b, c |
| x, y, z |
| r, v |
We think as a group queue
| x | y |
|---|
| r | v |
|---|
when pushing... check if the group it belongs is in group queue
if yes, push the corresponding queue
if no, push a new group into group queue and push element into that new queue
| a |
|---|
Parentheses matching
if left
put into stack
if right
check if it's match with top
if not
error
if matched
pop
Additional Question
Additional Question
Given an array of integer
ask about the first number on the right of number that greater than this number.
ex. 3 2 1 6 3 7 5 4 2 1 8 9
6 6 6 7 7 8 8 8 8 8 9 -1
Formal input description
the first line is an integer N, N <= 10^7
2nd line contains N integers
3rd line is an integer Q, Q<=10^7
and following Q lines
each line have one integer x, 0<=x<=N-1, represent the index
for each x, output the first element greater than x-th element on the right of x-th element
input:
8
3 2 5 7 4 3 9 1
5
3
2
5
1
4
output:
7
5
9
5
9
int seq[10006];
int ans[10006];
int main(){
cin >> N;
for(int i = 0; i < N; i++){
cin >> seq[i];
}
int Q;
cin >> Q;
int index;
for(int i = 0; i < Q; i++){
cin >> index;
for(int j = index; j < N; j++){
if(seq[j] > seq[index-1]){
cout << seq[j] << endl;
}
if(j == N-1){
cout << -1 << endl;
}
}
}
}What is the time complexity ??
How about we store all answer first?
int seq[10006];
int ans[10006];
int main(){
cin >> N;
for(int i = 0; i < N; i++){
cin >> seq[i];
}
for(int i = 0; i < N; i++){
for(int j = i + 1; j < N; j++){
if(seq[j] > seq[i]){
ans[j] = seq[i];
break;
}
if(j == N-1)
ans[j] = -1;
}
}
int Q;
cin >> Q;
int index;
for(int i = 0; i < Q; i++){
cin >> index;
cout << ans[index-1] << endl;
}
}What is the time complexity ??
Note
For i-th element
any element after it(j > i) but small than i-th element (seq[j] < seq[i])
can't be the answer of any element in front of i-th element
So we can... skip them!
And only record those who is possible be the anwer.
int seq[10006];
int ans[10006];
int main(){
cin >> N;
stack<int> S;
for(int i = 0; i < N; i++){
cin >> seq[i];
}
for(int i = N-1; i < N; i++){
while(!S.empty() && S.top() <= seq[i]){
S.pop();
}
if(S.empty())
ans[i] = -1;
else
ans[i] = S.top();
S.push(seq[i]);
}
int Q;
cin >> Q;
int index;
for(int i = 0; i < Q; i++){
cin >> index;
cout << ans[index-1] << endl;
}
}What is the time complexity ?? How many times does stack pop() operate ?
int seq[10006];
int ans[10006];
int main(){
cin >> N;
stack<int> S;
for(int i = 0; i < N; i++){
cin >> seq[i];
}
for(int i = N-1; i < N; i++){
while(!S.empty() && S.top() <= seq[i]){
S.pop();
}
if(S.empty())
ans[i] = -1;
else
ans[i] = S.top();
S.push(seq[i]);
}
int Q;
cin >> Q;
int index;
for(int i = 0; i < Q; i++){
cin >> index;
cout << ans[index-1] << endl;
}
}Every element only enter stack and pop out stack once
int seq[10006];
int ans[10006];
int main(){
cin >> N;
stack<int> S;
for(int i = 0; i < N; i++){
cin >> seq[i];
}
for(int i = N-1; i < N; i++){
while(!S.empty() && S.top() <= seq[i]){
S.pop();
}
if(S.empty())
ans[i] = -1;
else
ans[i] = S.top();
S.push(seq[i]);
}
int Q;
cin >> Q;
int index;
for(int i = 0; i < Q; i++){
cin >> index;
cout << ans[index-1] << endl;
}
}We can say that it is still O(n)
Stack & Queue
By tunchin kao
Stack & Queue
- 82



