Primer Questions

What is an algorithm?

Are all programs algorithms?

Primer Questions

What is the "runtime" of a program?

Primer Questions

How many operations will occur when I run this program?

var arr = [1, 2, 3, 4, 5];
var sum = 0;

while(i < arr.length) {
    sum += arr.length;
    i++;    
}

Primer Questions

2 + 3*5 = 17

var arr = [1, 2, 3, 4, 5];
var sum = 0;

while(i < arr.length) {
    sum += arr.length;  
    i++;  
}

At its heart, computing Big O is about counting the number of operations a program will run.

Big O -- Medium Formality

"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.

Big O

"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.

Theoretical: We're dealing with the abstraction, not necessarily a specific implementation.

Big O

"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.

Time or Memory: We can measure two categories of complexity.

Time complexity is the number of operations a program must execute before completing

Big O

"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.

Time or Memory: We can measure two categories of complexity.

Memory complexity is the amount of data that must be stored before the algorithm completes.

Big O

"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.

Problem Size n: The algorithmic complexity is based on the size of the input.

"Asymptotic Complexity"

The reason we measure algorithms in Big O is to determine how they behave as n gets very large.

In this way, Big O is kind of like limits in calculus. We care about the big o as n approaches infinity.

"Asymptotic Complexity"

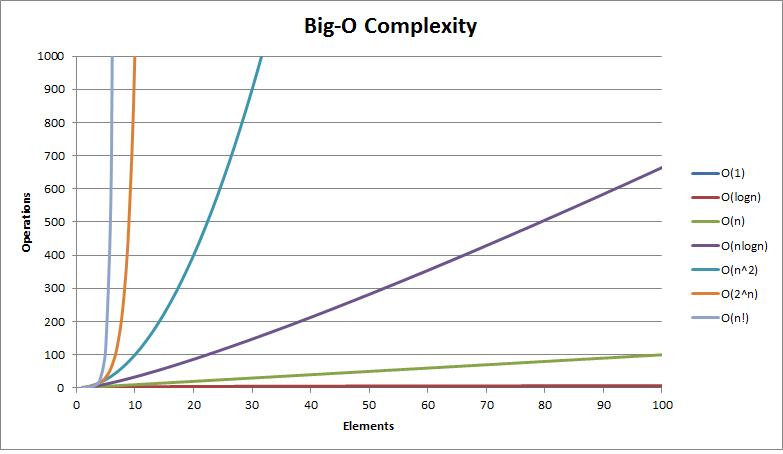
"Asymptotic Complexity"

With your table, discuss why computer scientists tend to only care about complexity as n gets large.
 

What are some potential drawbacks of this mentality?

"Asymptotic Complexity"

Consider this program:

function twoLoops(n) {
  let sum = 0;
  for(let i = 0; i < 100000000; i++) {
    sum += 1
  }

  for(let i = 0; i < n; i++) {
    sum += 1
  }
}

What is the time complexity Big O of this function?

function twoLoops(n) {
  let sum = 0;
  for(let i = 0; i < 100000000; i++) {
    sum += 1
  }

  for(let i = 0; i < n; i++) {
    sum += 1
  }
}

Can you plot the line/curve for our twoLoops function on this graph?

function print50nums() {
  for (var i = 0; i < 50; i++) {
    console.log(i);
  }
}

function print500000nums() {
  for (var i = 0; i < 500000; i++) {
    console.log(i);
  }
}

Binary Search (recursive)

function binarySearch(arr, lowIndex, highIndex, searchVal) {
    var sliceLength = highIndex - lowIndex;
    var midIndex = lowIndex + Math.floor(sliceLength / 2);
    var midVal = arr[midIndex];

    if(midVal === searchVal){
        return midIndex;
    }
    else if(lowIndex === highIndex) {
        return -1;
    }
    else if(searchVal < midVal) {
        return binarySearch(arr, lowIndex, midIndex - 1, searchVal);
    }
    else if(searchVal > midVal) {
        return binarySearch(arr, midIndex + 1, highIndex, searchVal);
    }
    else {
        throw new Error("Incompatible data -- no comparison returned true");
    }

    throw new Error("Reached what should be unreachable code.");
}

Binary Search (iterative)

function binaryIndexOf(searchElement) { 
    var minIndex = 0;
    var maxIndex = this.length - 1;
    var currentIndex;
    var currentElement;
 
    while (minIndex <= maxIndex) {
        currentIndex = (minIndex + maxIndex) / 2 | 0;
        currentElement = this[currentIndex];
 
        if (currentElement < searchElement) {
            minIndex = currentIndex + 1;
        }
        else if (currentElement > searchElement) {
            maxIndex = currentIndex - 1;
        }
        else {
            return currentIndex;
        }
    }
 
    return -1;
}

Iterative Fibonacci sequence

function fibbonacciIterative(n) {
	if(n <= 1) {
		return 1;
	}

	var fibNumber;
	var numberOne = 1;
	var numberTwo = 1;

	for(var i = 1; i < n; i++) {
		fibNumber = numberOne + numberTwo;
		numberOne = numberTwo;
		numberTwo = fibNumber;
	}

	return fibNumber;

}

Recursive Fibonacci sequence

function fibbonacciRecursive(n) {
	if(n <= 1) {
		return 1;
	}

	return fibbonacciRecursive(n - 1) + fibbonacciRecursive(n - 2);
}

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

reading the notation:

"F of n is said to be Big Oh of g of n"

THIS DEFINITION IS PURELY ACADEMIC

No employer that isn't a university will EVER care if you can describe Big O in this level of detail.

That doesn't mean it isn't worth examining...

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

This is full of "math-ese", which makes it a bit intimidating. Lets break it down with an example.

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

This equation is a statement about a function called f. Lets call this function f:

function f(arr) {
    var sum = 0;
    
    while(i < arr.length) {
        sum += arr.length;  
        i++;  
    }
}

Big O -- Formal

f(n) = O(g(n))

function f(arr) {
    var sum = 0;
    
    while(i < arr.length) {
        sum += arr.length; 
        i++;   
    }
}

n represents the "size of the input".

f( [1, 2, 3, 4] );          // n === 4
f( [1, 2, 3, 4, 5] );       // n === 5
f( [1, 2, 3, 4, 6, 7, 8] ); // n === 8

Big O -- Formal

f(n) = O(g(n))

Because the Big O notation is relative to the input size the Big O is a measure of how the algorithm scales.

function f(arr) {
    var sum = 0;
    
    while(i < arr.length) {
        sum += arr.length;
        i++; 
    }
}

Big O -- Formal

f(n) = O(g(n))

An equation for the operations run by this algorithm:

Ops = 1 + 3*arr.length

Ops = 1 + 3n

f(n) = O(c1 + c2*n)

f(n) = O(n)

function f(arr) {
    var sum = 0;
    
    while(i < arr.length) {
        sum += arr.length;
        i++; 
    }
}

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

Ops = 1 + 3n

f(n) == O(c1 + c2*n) == O(n)

f(n) is said to be O(n)

g(n) is the stand in for our magnitude: n

As soon as n > 3, the size of n "dominates" the equation 1+3*n

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

This "domination" is the core of Big O.

For every algorithm, there comes a point where the size of the input becomes more important than any other factor.

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

Recall:

f(n) = 1 + 3n

so, it is true that 0 ≤ f(n) ≤ cg(n)

  for all n ≥ 4

k == 4, c == 1

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

Recall:

f(n) = 1 + 3n

Can we choose different values for c and k that still satisfy the question?

Big O -- Formal

f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

Recall:

f(n) = 1 + 50n + 2n^2

What is the big O of this new formula?

What are valid some choices of c and k?