Extracting Structured Data from Web Pages

Arvind Arasu & Hector Garcia-Molina , 2003

Yan-Kai Lai, Yu-An Chou

Outline

• Abstract
• Introduction
• Structured Data
• Model of Page Creation
• Optionals and Disjunctions
• Problem Statement
• EXALG Approach
• Concusion

Abstract

• Many web sites contain large sets of pages generated using a common template or layout.
• We study the problem of automatically extracting the database values from such template- generated web pages without any learning examples or other sim- ilar human input.

Introduction

• There are, however, many web sites that have large collections of pages containing structured data, i.e., data having a structure or a schema.
• These pages are typically generated dynamically from an underlying structured source like a relational database.

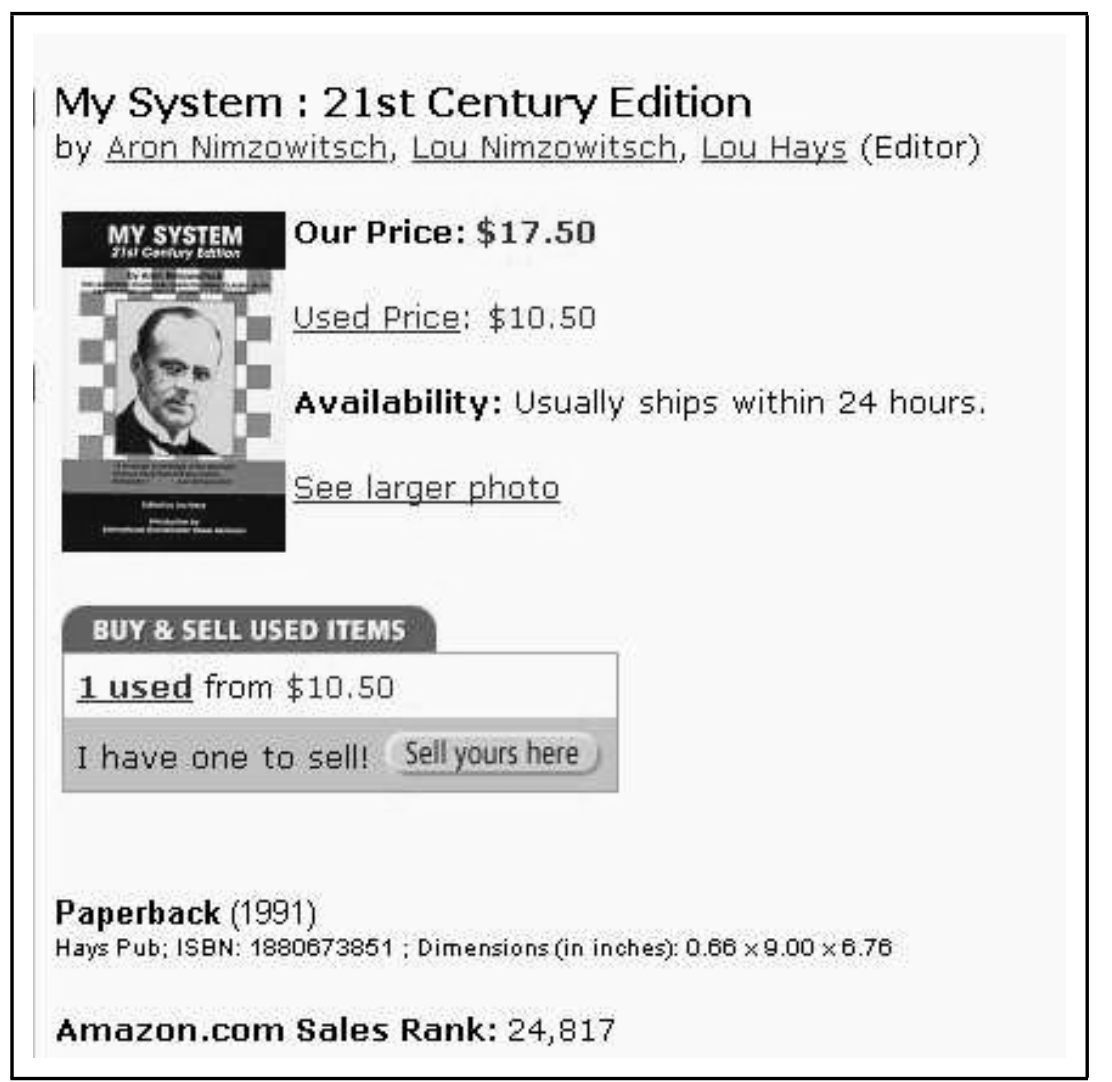
Introduction

• The above pages are generated using a common “template” by “plugging-in” values for the title, list of authors and so on.
• There are two fundamental challenges in automatically deducing the template
  • There is no obvious way of differentiating between text that is part of template and text that is part of data
  • the schema of data in pages is usually not a “flat” set of attributes, but is more complex and semi-structured.

Structured Data

• Structured Data is any set of data values conforming to a common schema or type. A type is defined recursively as follows
  1. The Basic Type, denoted by B, represents a string of tokens. A token is some basic unit of text. For the rest of the paper, we define a token to be a word or a HTML tag.
  2. If T1,...,Tn are types, then their ordered list ⟨T1,...,Tn⟩ is also a type. We say that the type ⟨T1,...,Tn⟩ is constructed from the types T1,...,Tn using a tuple constructor of order n.
  3. If T is a type, then {T} is also a type. We say that the type {T} is constructed from T using a set constructor.

Structured Data

• We use the term type constructor to refer to either a tuple or set constructor. An instance of a schema is defined recursively as follows.
  1. An instance of the basic type, B, is any string of tokens.
  2. An instance of type ⟨T1, T2,...,Tn⟩ is a tuple of the form ⟨i1, i2,...,in⟩ where i1, i2,...,in are instances of types T1, T2,...,Tn, respectively. Instances i1, i2,...,in are called attributes of the tuple.
  3. An instance of type {T} is any set of elements {e1,...,em}, such that ei(1 ≤ i ≤ m) is an instance of type T

Structured Data

• Each page contains the title, the set of authors, and the cost of a book. Further, each author has a first name and a last name. Then the schema of the data encoded in the pages is:
  • S1 = ⟨B, {⟨B, B⟩τ3 }τ2 , B⟩τ1
•  An instance of S1 is the value x1 = ⟨t, {⟨f1, l1⟩,⟨f2, l2⟩}, c⟩

Model of Page Creation

• A template T for a schema S, is de- fined as a function that maps each type constructor τ of S into an ordered set of strings T(τ ), such that,
  1. If τ is a tuple constructor of order n, T(τ ) is an ordered set of n + 1 strings ⟨Cτ1,...,Cτ(n+1)⟩.
  2. If τ is a set constructor, T(τ ) is a string Sτ (trivially an ordered set of unit size).

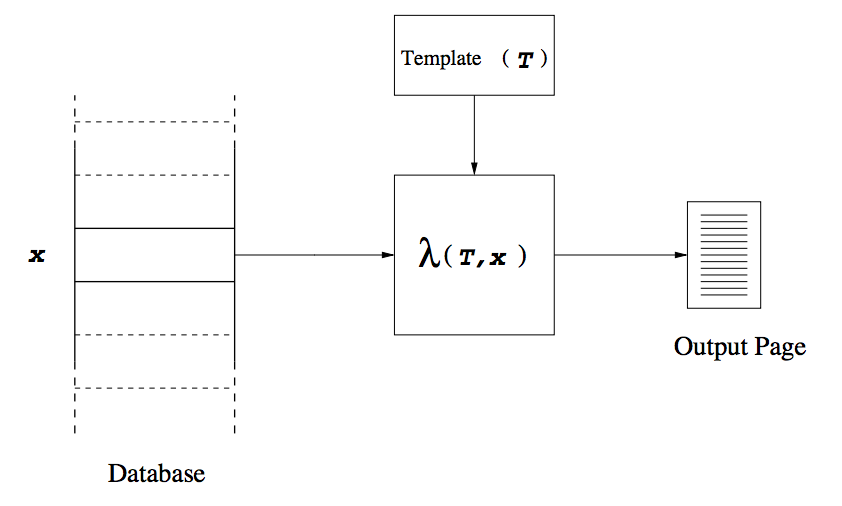
Model of Page Creation

• A template T1 S1 for Schema S1 is given by the mapping,
  • T1(τ1) = ⟨A, B, C, D⟩
  • T1(τ2) = H
  • T1(τ3) = ⟨E,F, G⟩
• the encoding λ(T1, x1) is the string 
• The web page corresponding to the book tuple
  • ⟨ C Programming Language, { ⟨ Brian, Kernighan⟩, ⟨ Dennis,Ritchie ⟩ }, $30.00 ⟩

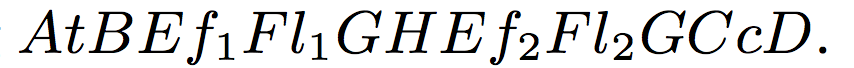
Optionals and Disjunctions

• There are two other kinds of type constructors that occur commonly in the schema of web pages, namely, optionals and disjunctions.
•  If T is a type, then (T)? represents the optional type T, and is equivalent to {T}τ with the constraint that in any instantiation τ has a cardinality of 0 or 1.
• Similarly, if T1 and T2 are types, (T1 | T2) represents a type which is disjunction of T1 and T2, and is equivalent to                          where for every instantiation of τ exactly one of τ1, τ2 has cardinality one and the other, cardinality zero.

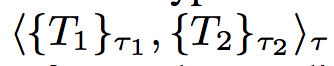
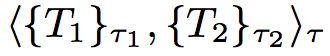
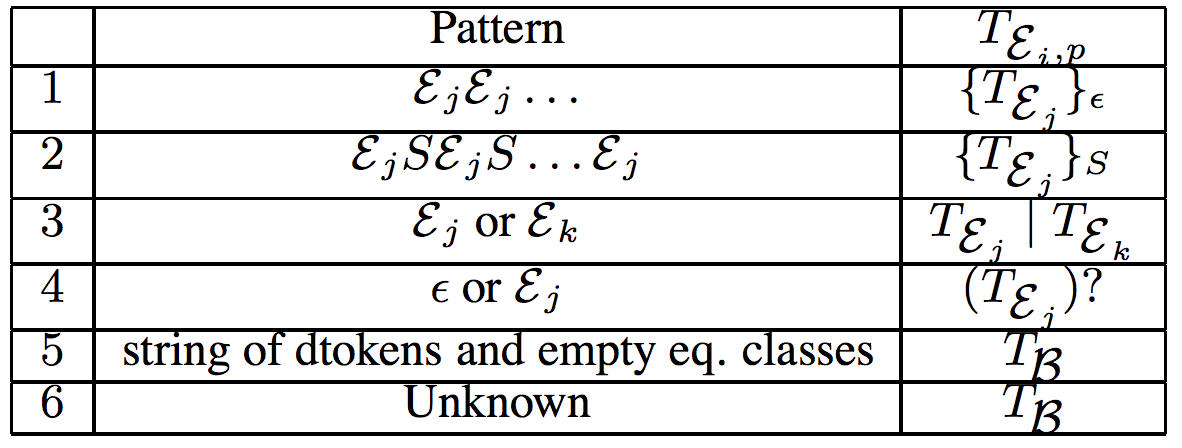
 Problem Statement

Equivalence Classes

• Occurrence Vector: The occurrence-vector of a token t, is defined as the vector ⟨f1,...,fn⟩, where fi is the number of occurrences of t in pi.
• Equivalence Class: An equivalence class is a maximal set of tokens having the same occurrence-vector

EXALG Approach​

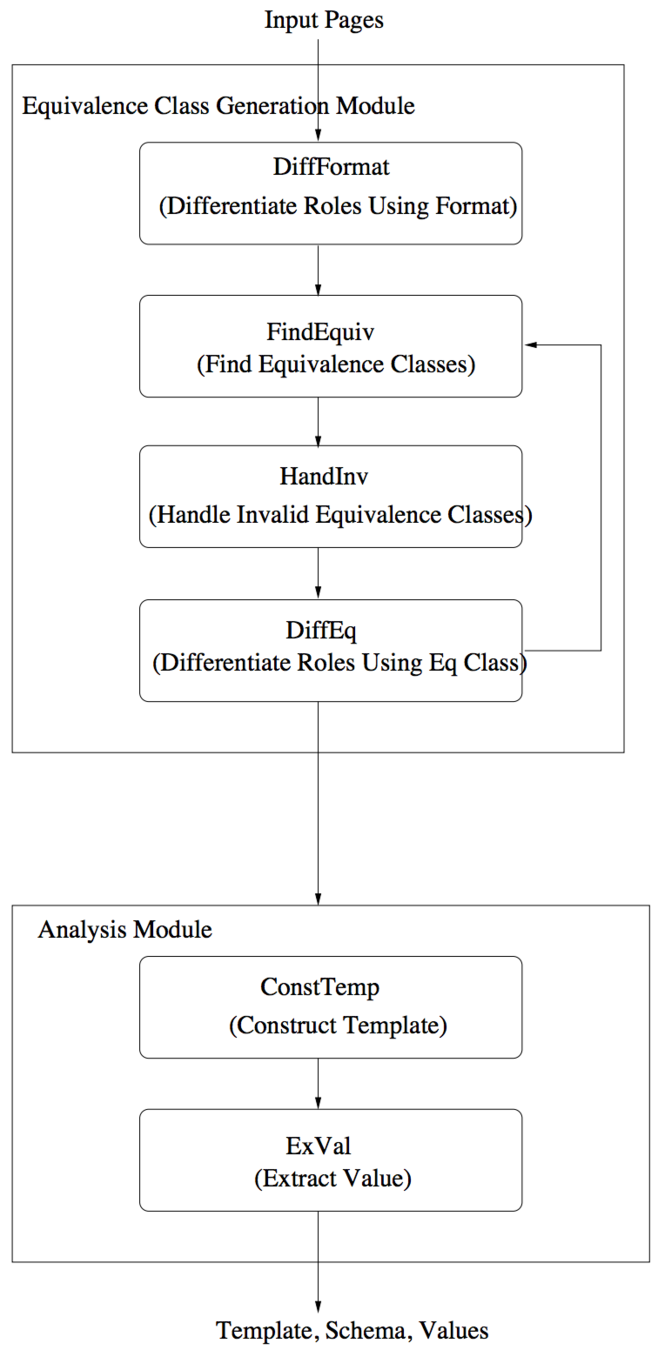
• In the first stage (ECGM), it discovers sets of tokens associated with the same type constructor in the (unknown) template used to create the input pages.
•  In the second stage (Analysis), it uses the above sets to deduce the template. The deduced template is then used to extract the values encoded in the pages. This section outlines the execution of EXALG for our running example.

EXALG Approach​

EXALG Approach​

• First, EXALG, infers (within Sub-module DIFFFORM) 3 that the “role” of Name when it occurs in Book Name is different from the “role” when it occurs in Reviewer Name, using the fact that these two occurrences always have different paths from the root in the html parse trees of the pages.

EXALG Approach​

• Second, EXALG (within Sub-module FINDEQ) computes “equivalence classes” — sets of tokens having the same frequency of occurrence in every page in Pe. EXALG retains only the equivalence classes that are large and whose tokens occur in a large number of input pages. We call such equivalence classes LFEQs (for Large and Frequently occurring EQuivalence classes).

EXALG Approach​

EXALG Approach​

EXALG Approach​

• 3rd, Module HANDINV takes as input a set of LFEQs (determined by FINDEQ), detects the existence of invalid LFEQs using violations of ordered and nesting properties, and “processes” the invalid LFEQs found

EXALG Approach​

• 4th, This section presents a powerful technique, called differentiating roles of tokens.
• Briefly, when we differentiate roles of tokens, we identify “contexts” such that the occurrences of a token in different contexts above necessarily have different roles.

EXALG Approach​

• The output template of CONSTTEMP is the template corresponding to the root equivalence class — the equivalence class with occurrence vector ⟨1, 1, ···⟩ 8 .

Conclusion

• This paper presented an algorithm, EXALG, for extracting structured data from a collection of web pages generated from a common template.
• EXALG uses two novel concepts, equivalence classes and differentiating roles, to discover the template.