Оценка неопределенности предсказания нейросетей байесовскими методами

По мотивам работ Yarin Gal & Zoubin Ghahramani

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

История байесовских нейросетей

John Denker & John Hopfield, 1987
Naftali Tishby, Esther Levin, Sara Solla, 1989
John Denker & Yann LeCun, 1991
David MacKay, 1992
Radford Neal, 1993
Christopher K.I. Williams 1996

История байесовских нейросетей

David MacKay

История байесовских нейросетей

Radford Neal

BNN with infinite latent layer = gaussian process
Automatic relevance determination
Hamiltonian Monte Carlo

Ссылки:

Доклад Зубина Гарамани на NIPS 2016: https://www.youtube.com/watch?v=FD8l2vPU5FY
Доклад Ярина Гала в Microsoft Research: https://www.youtube.com/watch?v=YAb5C5_g-kk
Блог-диссертация Ярина Гала: http://mlg.eng.cam.ac.uk/yarin/blog_3d801aa532c1ce.html
Современное положение дел в области: https://wjmaddox.github.io/assets/BNN_tutorial_CILVR.pdf

История байесовских нейросетей

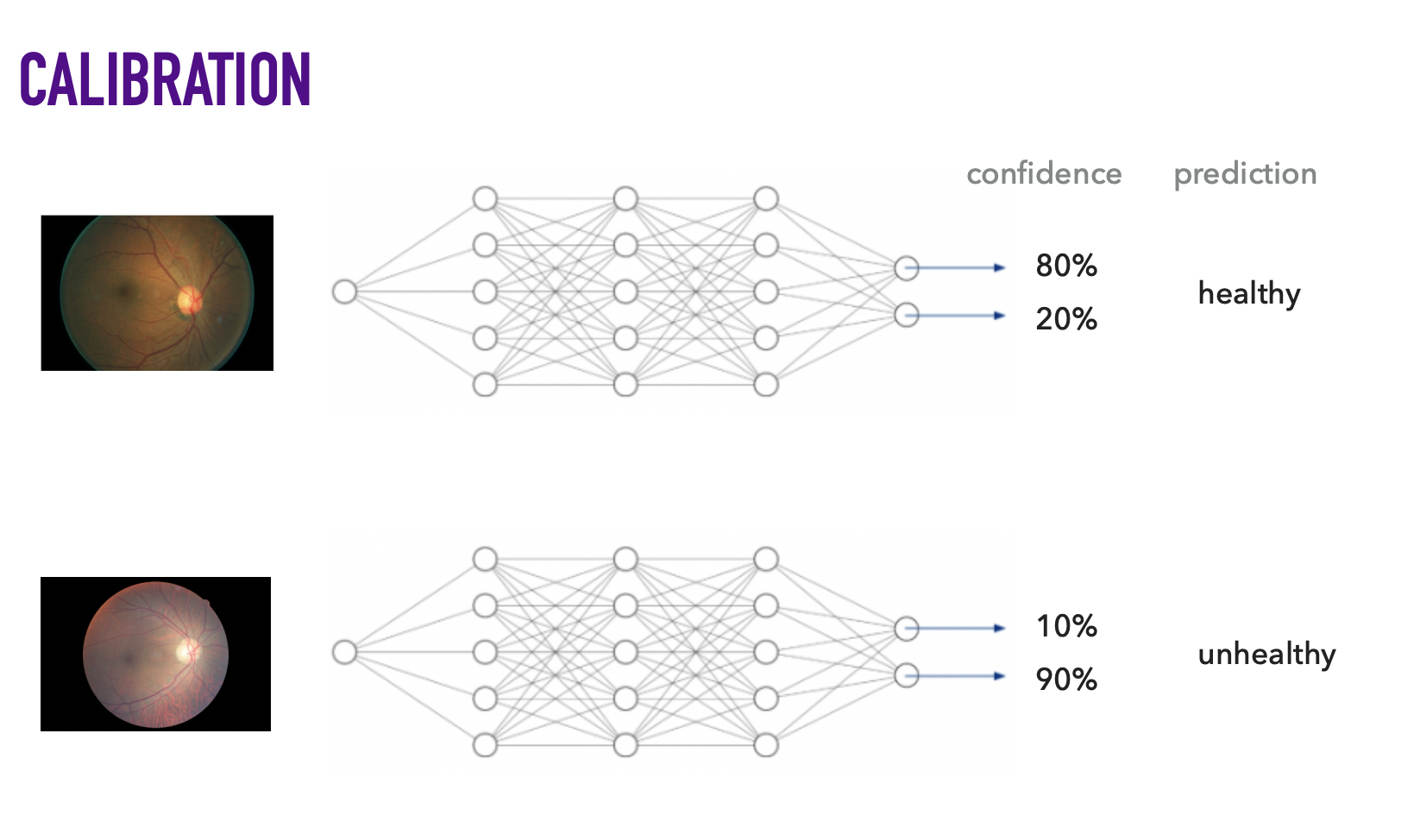
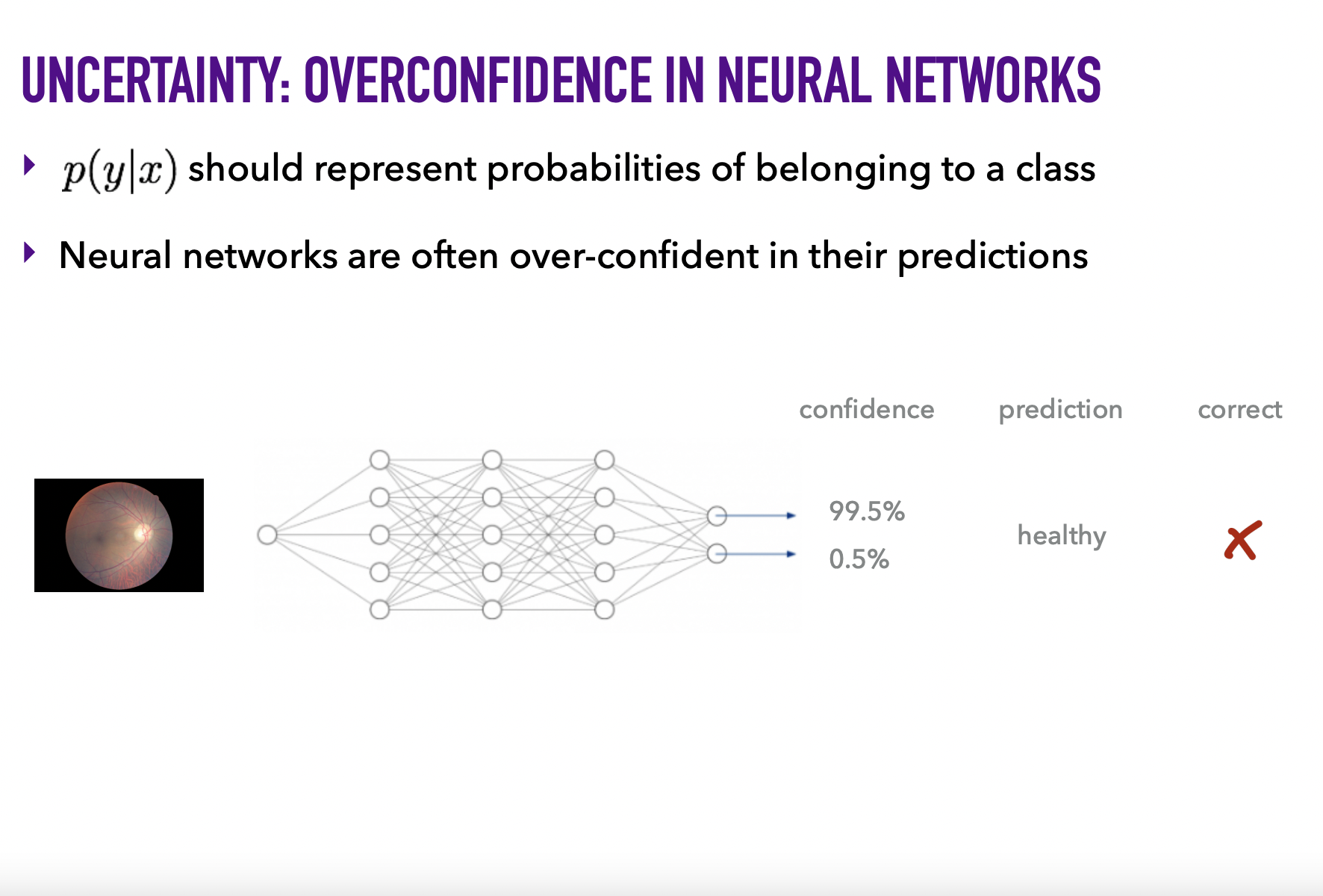
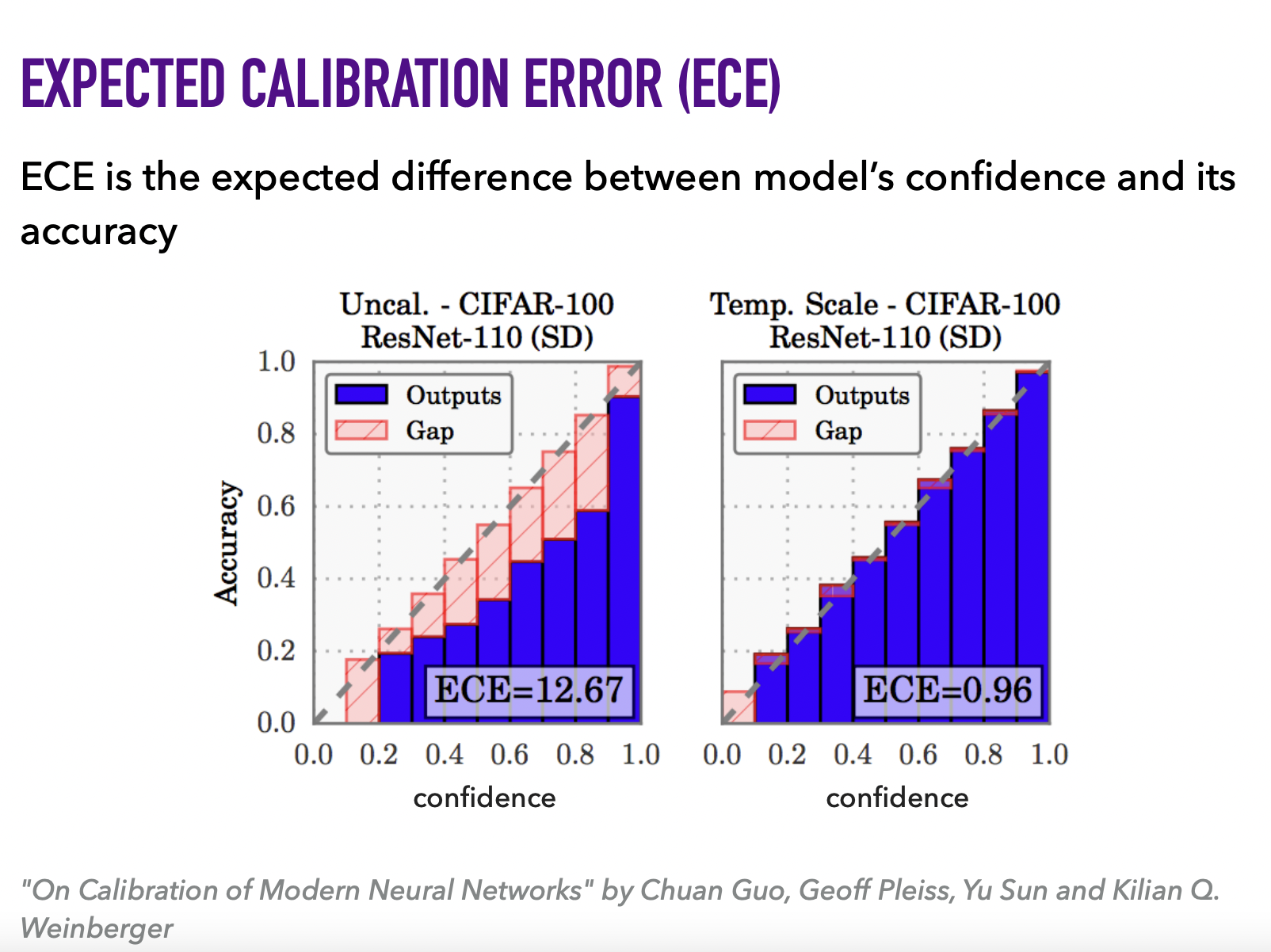
Из https://wjmaddox.github.io/assets/BNN_tutorial_CILVR.pdf

Предостережение: опасно рассматривать число от 0 до 1, возвращаемое predict_proba(), как степень уверенности модели. Нельзя просто применить сигмоиду/софтмакс/z-score и считать это вероятностью.

Пререквизиты для BNN

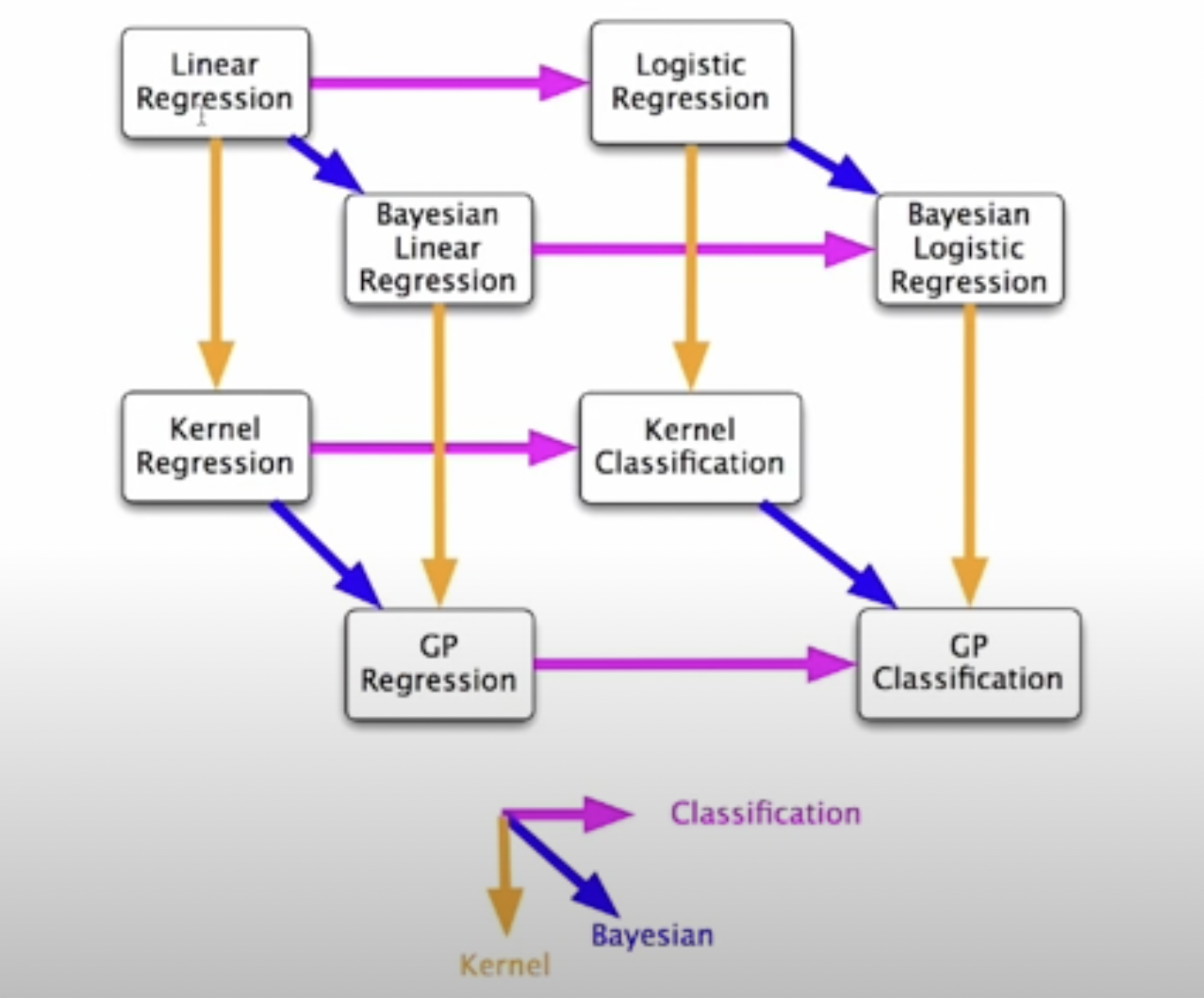
Z. Ghahramani, NIPS 2016: https://www.youtube.com/watch?v=FD8l2vPU5FY

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

Байесовская линейная регрессия

f(x) = x^T \cdot w

y = f(x) + \epsilon

\epsilon \sim \mathcal{N}(o, \sigma^2_n)

Байесовская линейная регрессия

Из Rasmussen, Williams: Gaussian Processes (2006)

Сумму наименьших квадратов можно рассматривать как многомерное нормальное распределение.

Байесовская регрессия

Из Rasmussen, Williams: Gaussian Processes (2006)

Байесовская линейная регрессия с гауссовским prior'ом эквивалентна ridge-регрессии (линейной регрессии с тихоновской l2-регуляризацией)

Байесовская регрессия

Из Rasmussen, Williams: Gaussian Processes (2006)

Байесовскую линейную регрессию можно рассматривать как ансамбль моделей, по предсказаниям которого мы берем взвешенное среднее.

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

Kernel ridge regression

Осторожно: не путайте kernel ridge regression c kernel regression (например, вычисляемый с помощью Nadaraya-Watson estimator, это другой метод):

https://stats.stackexchange.com/questions/312929/is-kernel-ridge-regression-the-same-as-kernel-regression

Kernel ridge regression

Что делать, если нам нужно смоделировать нелинейную зависимость целевой переменной от независимых переменных?

Можно сделать ту же самую линейную регрессию с регуляризацией, только в качестве факторов использовать полиномы от независимой переменной:

\phi(x) = \begin{bmatrix} 1 \\ x \\ x^2 \\ x^3 \\ \cdots \end{bmatrix}

f(x) = \phi(x)^T \cdot w

Kernel ridge regression

Из Rasmussen, Williams: Gaussian Processes (2006)

Kernel ridge regression

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

Гауссовы процессы

Переход от многомерного нормального распределения как в байесовской линейной регрессии к бесконечномерному вектору - функции.

\begin{bmatrix} f(x_1) \\ f(x_2) \\ \cdots \\ f(x_n) \end{bmatrix}, (f(x_i), f(x_j)) \sim \mathcal{N}(\mu, \Sigma)

\mu = \begin{bmatrix} \mu_{1} \\ \cdots \\ \mu_{n} \end{bmatrix}, \Sigma = \begin{bmatrix} k(x_1, x_1) \ldots k(x_1, x_n) \\ \cdots \cdots \cdots \\ k(x_n, x_1) \ldots k(x_n, x_n) \end{bmatrix}

Гауссовы процессы

Ссылки:

C.Williams, K.Rasmussen - Gaussian processes:
http://www.gaussianprocess.org/gpml/chapters/
R.Neal - thesis
C.Williams - computing with infinite networks: https://proceedings.neurips.cc/paper/1996/file/ae5e3ce40e0404a45ecacaaf05e5f735-Paper.pdf
Visual exploration of Gaussian processes: https://distill.pub/2019/visual-exploration-gaussian-processes/
https://peterroelants.github.io/posts/gaussian-process-tutorial/
Neil Lawrence: http://inverseprobability.com/talks/notes/gaussian-processes.html

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

Вариационный вывод

p(x, \theta) = p(x | \theta) \cdot p(\theta) = p(\theta | x) \cdot p(x)

likelihood

prior

posterior

evidence

Задача: вычислить posterior.

Препятствие: проблема обычно состоит в том, что evidence is intractable.

p(x) = \int p(x | \theta) p(\theta) d{\theta}

- не вычисляемо

Вариационный вывод

p(\theta | x) \approx q(\theta) \in \mathcal{Q}

KL(q(\theta) \Vert p(\theta | x)) \to \min\limits_{q(\theta) \in \mathcal{Q}}

KL(q(\theta) \Vert p(\theta | x)) = \int q(\theta) \log \frac{q(\theta)}{p(\theta | x)} d\theta \ge 0

Из лекции Д.Ветрова на DeepBayes2019

Вариационный вывод

\log p(x) = \int q(\theta) \log{p(x)} d\theta = \int q(\theta) \log \frac{p(x, \theta)}{p(\theta | x)} d\theta

= \int q(\theta) \log \frac{p(x, \theta) q(\theta)}{p(\theta | x) q(\theta)} d\theta

= \int q(\theta) \log \frac{p(x, \theta)}{q(\theta)} d\theta + \int q(\theta) \log \frac{q(\theta)}{p(\theta | x)} d\theta

= \mathcal{L}(q(\theta)) + KL(q(\theta) \Vert p(\theta | x))

Из лекции Д.Ветрова на DeepBayes2019

ELBO

\log p(x) = \mathcal{L}(q(\theta)) + KL(q(\theta) \Vert p(\theta | x))

ELBO - Evidence lower bound

KL \ge 0 \Rightarrow \log p(x) \ge \mathcal{L}(q(\theta))

KL(q(\theta) \Vert p(\theta | x)) \to \min \Leftrightarrow \mathcal{L}(q(\theta)) \to \max

Из лекции Д.Ветрова на DeepBayes2019

ELBO

\mathcal{L}(q(\theta)) = \int q(\theta) \log \frac{p(x, \theta)}{q(\theta)} d\theta = \int q(\theta) \log \frac{ p(x|\theta) p(\theta) }{q(\theta)} d\theta

Из лекции Д.Ветрова на DeepBayes2019

= \int q(\theta) \log p(x| \theta) d\theta + \int q(\theta) \log \frac{ p(\theta) }{q(\theta)} d\theta

= \mathbb{E}_{ q(\theta) } \log p(x|\theta) - KL(q(\theta) \Vert p(\theta))

Expected log-likelihood

Regulariser term

KL-divergence

Стохастический вариационный вывод

Литература:

Тьюториал David Blei: https://arxiv.org/pdf/1601.00670.pdf - через Natural gradient descent - обеспечивает равное убывание KL divergence по всем направлениям движения, основан на Fisher information matrix (см. https://towardsdatascience.com/natural-gradient-ce454b3dcdfa)
Статья Kingma, Welling по VAE: https://arxiv.org/pdf/1312.6114.pdf
Лекция Дмитрия Ветрова по VI и ELBO: https://www.youtube.com/watch?v=xH1mBw3tb_c
Лекция Дмитрия Ветрова по SVI и VAE: https://www.youtube.com/watch?v=tjT4Wf86FMM

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

Uber Pyro

VAE SVI in Pyro

ScanVI in Pyro

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

Дропаут как регуляризация нейронных сетей

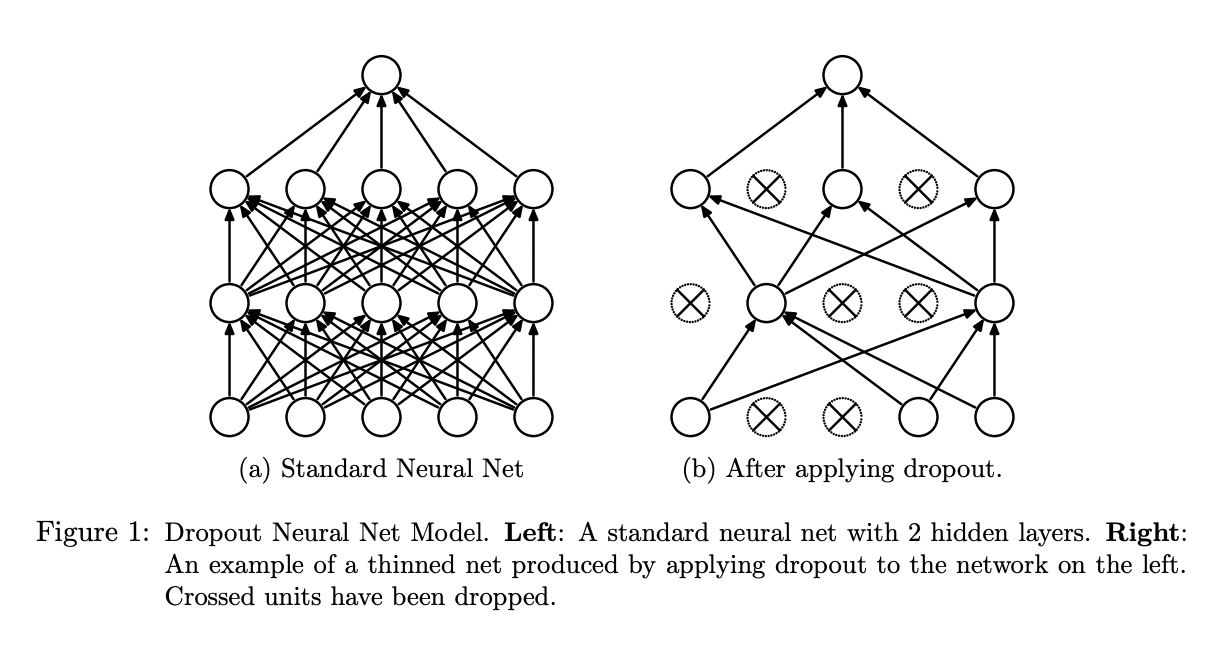
Бинарный или бернуллиевский дропаут

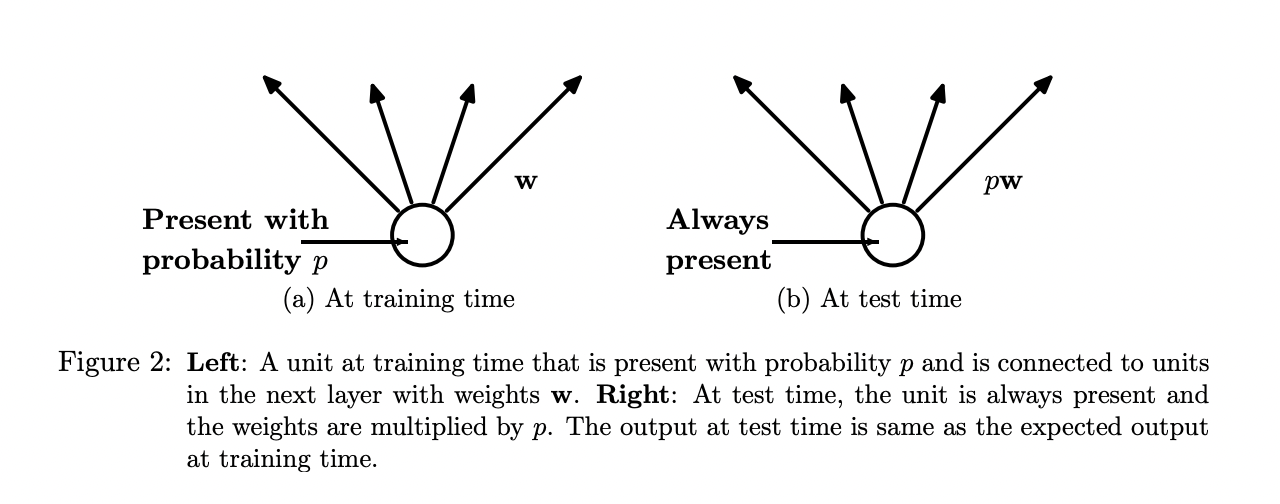
Аналогия с половым размножением - каждая модель

в ансамбле передает половину своих весов потомству с вероятностью p (исходно - 0.5).

Гауссовский дропаут

Srivastava, Hinton et al. позже показали, что Гауссовский Дропаут с непрерывным шумом работает не хуже и быстрее.

\xi_\mu \sim \mathcal{N}(1, \alpha=\frac{p}{(1-p)})

Дропаут

Hinton 2012: https://arxiv.org/pdf/1207.0580.pdf
Srivastava, Hinton 2014a: https://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf

План доклада

История байесовских нейросетей
Байесовская регрессия
Kernel ridge regression
Гауссовы процессы
Вариационный вывод и ELBO, стохастический вариационный вывод
Библиотека вероятностного программирования Uber Pyro
Регуляризация нейросетей, бинарный и гауссовский дропаут
Вариационный дропаут

Вариационный дропаут

Байесовская нейронная сеть с бесконечным числом нейронов в скрытом слое ведет себя как гауссовский процесс.

Вариационный дропаут

http://mlg.eng.cam.ac.uk/yarin/blog_3d801aa532c1ce.html

Вариационный дропаут

https://polit.ru/article/2014/05/04/pigarev/

Automatic Relevance Determination или Relevance Vector Machines применительно к висцеральной теории сна.

Вариационный дропаут

Ссылки

Молчанов, Ашуха, Ветров, 2017:
https://arxiv.org/pdf/1701.05369.pdf
Kingma, Salimans, Welling, 2015:
https://arxiv.org/pdf/1506.02557.pdf
Gal, Ghahramani, 2016:
https://arxiv.org/pdf/1506.02142.pdf

Оценка неопределенности предсказания нейросетей байесовскими методамим

By vasjaforutube1

Оценка неопределенности предсказания нейросетей байесовскими методамим