SROVNÁNÍ DVOU PRŮMĚRŮ A JEDNODUCHÁ ANALÝZA SOUVISLOSTI

Vít Gabrhel

vit.gabrhel@mail.muni.cz

FSS MU,

9. 10. 2017

Harmonogram

 0. Rekapitulace předchozí hodiny

 

 1. Deskriptivní statistiky - doplnění 

 

 2. Srovnání dvou průměrů

 

 3. Chí-kvadrát

 

 4. Korelace

 

 

Rekapitulace

Skript

# Jakou třídu (class) tvoří obě proměnné?

class(alco_1$Country)
class(alco_1$Litry)

 

lapply(Alco, class)

# Změňte tuto hodnotu na "NA"

alco_1$Litry[alco_1$Litry == "-99"] <- NA

Alco$Litry <- str_replace(Alco$Litry,-99.00, "NA")

Alco[46,2] = NA

# Jedna z hodnot je evidentně špatně evidovaná. O jakou hodnotu se jedná?

chyby = subset(alco, subset = (Litry < 0))

# V této nové matici ať jsou všechny země napsané velkými písmeny.

Alco_2 [,"Stát"] = toupper(Alco_2[,"Stát"])

Deskriptivní statistiky

Rozšiřující možnosti

setwd()

library("readxl")

talent_scores_sheets = excel_sheets("talent_scores.xlsx")
talent_scores = read_excel("talent_scores.xlsx", sheet = 1)

 

# Compute the mean of the scores for each student individually
rowMeans(talent_scores[, 2:6])

 

# Compute the mean of the scores for each course individually
colMeans(talent_scores[, 2:6])

 

# Compute the score each student has gained for all his courses
rowSums(talent_scores[, 2:6])

 

# Compute the total score that is gained by the students on each course
colSums(talent_scores[, 2:6])

Deskriptivní statistiky

Rozšiřující možnosti

wm = read.csv2("wm.csv", header = TRUE)

 

mean(wm$gain) # function: computes the arithmetic mean
mean(wm$gain, na.rm = TRUE) # function: computes the arithmetic mean
median(wm$gain) # function: computes the median
var(wm$gain) # function: computes the variance
sd(wm$gain) # function: computes the standard deviation
min(wm$gain) # function: return the minimum
max(wm$gain) # function: return the maximum

 

# Summary statistics for all variables - 5 digits
summary(wm, digits = 5)

 

# Summary statistics for all variables - 10 digits
summary(wm, digits = 10)

Deskriptivní statistiky

Rozšiřující možnosti

library("dplyr")

# Calculate summary statistics for variables containing "ai". Calculate the statistics to 4 significant digits
summary(select(wm, contains("ai")))

 

# Alternatively, the numSummary() function might be used to obtain some summary statistics. The function computes:

• mean= the mean
• sd = the standard deviation
• iqr = the interquartile range
• 0% = the minimum
• 25% = the 1st quantile or the lower quartile
• 50% = the median
• 75% = the 3rd quantile or the upper quartile
• 100%= the maximum
• n = the number of observations

library("Rcmdr")
numSummary(wm$gain)

 

library("Hmisc")
describe(wm)

Korelace

Úvod (dle Pearson product-moment correlation coefficient, n.d.)

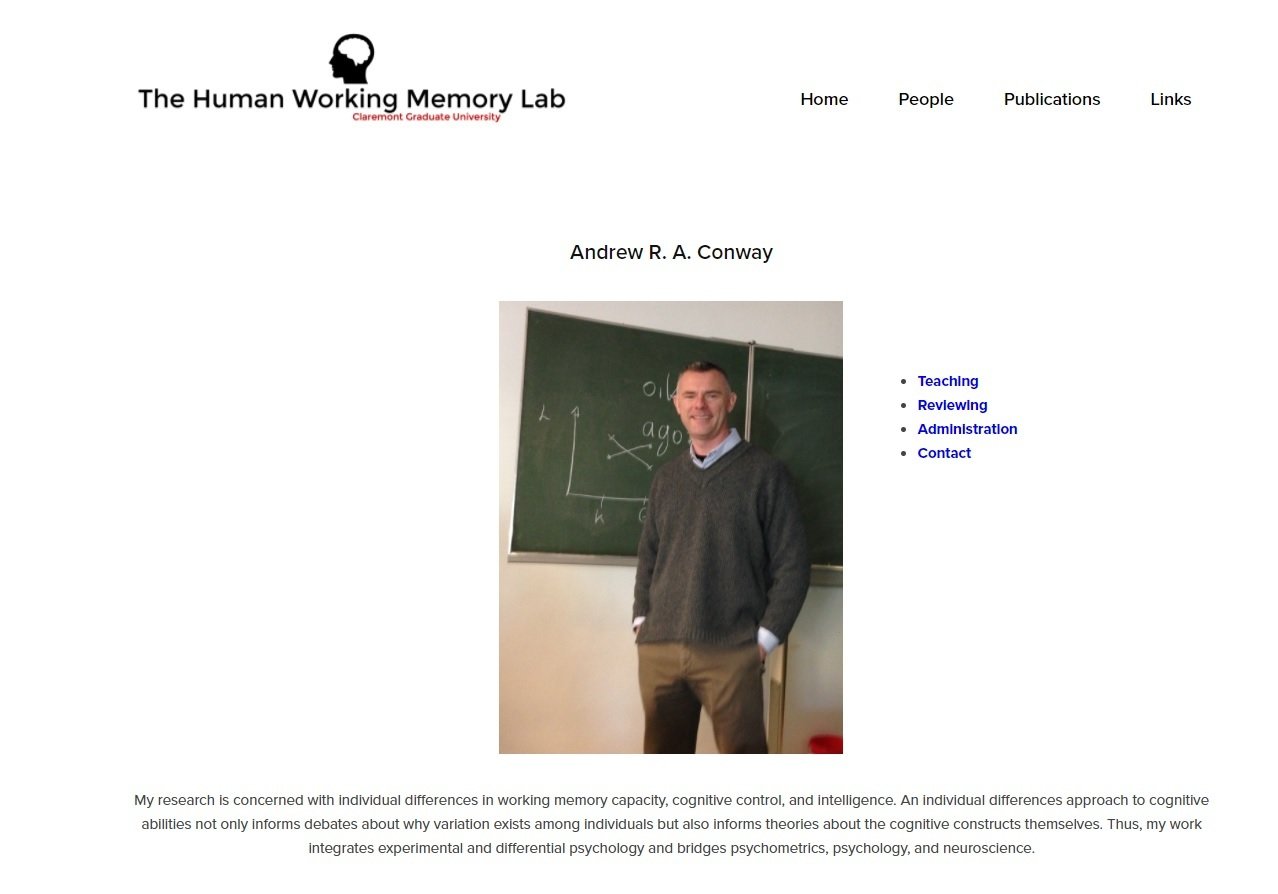
Pearson product-moment correlation coeficient

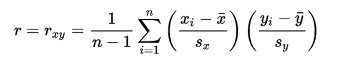
Předpoklady použití:

• Alespoň intervalová úroveň měření proměnných
• Normálně rozložená data
• Homoskedascita

Korelace

base

# Read the variables names
names(talent_scores)

 

# Create a subset of the dataframe talent, talent_selected, containing reading, english and math (in that order)
talent_selected <- subset(talent_scores, select = c(reading, english, math))

 

# Předpoklady pro použití

hist(talent_selected$english, main="Histogram for English scores", xlab="Students", border="blue", col="green", xlim=c(0,120), breaks=20)

 

plot(talent_selected$english, talent_selected$math, main="Scatterplot of Grades", xlab="English ", ylab="Math", pch=19)

 

qqnorm(talent_selected$math)

 

Korelace

base

# Compute the correlations among reading, english and math
cor(talent_selected)

 

#The cor() function does not calculate p-values to test for significance, but the cor.test() function does.
cor.test(talent_selected$english, talent_selected$reading, use = pairwise)
cor.test(talent_selected$reading, talent_selected$math, use = pairwise)
cor.test(talent_selected$english, talent_selected$math, use = pairwise)

Korelace

Rcmdr

# The rcorr.adjust() function of the Rmcdr package computes the correlations with the pairwise p-values among the correlations.

 

library("Rcmdr")

 

# Two types of p-values are computed: the ordinary p-values and the adjusted p-values.

?rcorr.adjust

rcorr.adjust(talent_selected)
 

 

# Test the significance of the correlations among `english` and `math`
cor.test(talent_selected$english, talent_selected$math, use = pairwise)

Srovnání dvou průměrů (dle Conway, n.d.)

Dependent t-test - úvod

Předpoklady použití:

• The sampling distribution is normally distributed. In the dependent t-
  test this means that the sampling distribution of the differences between scores should be normal, not the scores themselves.
• Data are measured at least at the interval level.

Srovnání dvou průměrů

Dependent t-test - base - argumenty

# Data

wm_t <- subset(wm, wm$train == "1")

# In the case of our dependent t-test, we need to specify these arguments to t.test():

?t.test
 
# x: Column of wm_t containing post-training intelligence scores
# y: Column of wm_t containing pre-training intelligence scores
# paired: Whether we're doing a dependent (i.e. paired) t-test or # # independent t-test. In this example, it's TRUE
# Note that t.test() carries out a two-sided t-test by default

Srovnání dvou průměrů

Dependent t-test - base - kód

# Conduct a paired t-test using the t.test function
t.test(wm_t$post, wm_t$pre, paired = TRUE)

Output:

Paired t-test

data:  wm_t$post and wm_t$pre
t = 14.492, df = 79, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 3.008511 3.966489
sample estimates:
mean of the differences
                 3.4875

Srovnání dvou průměrů (dle Conway, n.d.)

Dependent t-test - Cohenovo d

Srovnání dvou průměrů

Dependent t-test - Cohenovo d - lsr - argumenty

library("lsr")

# For cohensD(), we'll need to specify three arguments:

# x: Column of wm_t containing post-training intelligence scores
# y: Column of wm_t containing pre-training intelligence scores
# method: Version of Cohen's d to compute, which should be "paired" in this case

?cohensD()

Srovnání dvou průměrů

Dependent t-test - Cohenovo d - lsr - output

# Calculate Cohen's d
cohensD(wm_t$post, wm_t$pre, method = "paired")

[1] 1.620297

Srovnání dvou průměrů

Dependent t-test - Cohenovo d - effsize - argumenty

library("effsize")

cohen.d(x, y, pooled=TRUE, paired=TRUE,
        na.rm=FALSE, hedges.correction=FALSE,
        conf.level=0.95, noncentral=FALSE)

?cohen.d()

Srovnání dvou průměrů

Dependent t-test - Cohenovo d - effsize - příklad

library("effsize")

cohen.d(wm_t$post,wm_t$pre,pooled=TRUE,paired=TRUE,
        na.rm=FALSE, hedges.correction=FALSE,
        conf.level=0.95,noncentral=FALSE)

Srovnání dvou průměrů (dle Conway, n.d.)

Independent t-test - úvod

Předpoklady použití:

• The sampling distribution is normally distributed.
• Data are measured at least at the interval level.
• Homogeneity of variance.
• Scores are independent (because they come from different people).

Srovnání dvou průměrů

Independent t-test - data

# View the wm_t dataset
wm_t

 

# Create subsets for each training time
wm_t08 <- subset(wm_t, subset = (wm_t$cond == "t08"))
wm_t12 <- subset(wm_t, subset = (wm_t$cond == "t12"))
wm_t17 <- subset(wm_t, subset = (wm_t$cond == "t17"))
wm_t19 <- subset(wm_t, subset = (wm_t$cond == "t19"))

 

# Summary statistics for the change in training scores before and after training
describe(wm_t08)
describe(wm_t12)
describe(wm_t17)
describe(wm_t19)

 

# Create a boxplot of the different training times
ggplot(wm_t, aes(x = cond, y = gain, fill = cond)) + geom_boxplot()

 

# Levene's test
leveneTest(wm_t$gain ~ wm_t$cond)

Srovnání dvou průměrů

Independent t-test - base

# Conduct an independent t-test
t.test(wm_t19$gain, wm_t08$gain, var.equal = FALSE)

 

Welch Two Sample t-test

data:  wm_t19$gain and wm_t08$gain
t = 8.9677, df = 34.248, p-value = 1.647e-10
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 3.287125 5.212875
sample estimates:
mean of x mean of y
     5.60      1.35 

Srovnání dvou průměrů (dle Conway, n.d.)

Independent t-test - Cohen's d

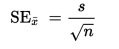
Srovnání dvou průměrů

Independent t-test - effsize

# Calculate Cohen's d

cohen.d(wm_t19$gain, wm_t08$gain,pooled=TRUE,paired=FALSE,
        na.rm=FALSE, hedges.correction=FALSE,
        conf.level=0.95,noncentral=FALSE)

 

Cohen's d

d estimate: 2.835822 (large)
95 percent confidence interval:
     inf      sup
1.893561 3.778083 

Chí-kvadrát (dle Pearson's chi-squared test, n.d.)

Úvod

Předpoklady použití:

• Ne méně než 20 % buněk v rámci kontigenční tabulky s hodnotou méně než 5

• Nenulová hodnota v každé z buněk v rámci kontingenční tabulky

Chí-kvadrát

Data a gmodels

# Data

• gedu_sheets = excel_sheets("gedu.xlsx")
• gedu = read_excel("gedu.xlsx", sheet = 1)
• gedu$Gender = as.factor(gedu$Gender)
• gedu$Edu = as.factor(gedu$Edu)
• gedu$Edu2 = as.factor(gedu$Edu2)
• levels(gedu$Gender) = c("Muž", "Žena")
• levels(gedu$Edu) = c("ZŠ", "SŠ bez maturity", "SŠ s maturitou", "VŠ")
• levels(gedu$Edu2) = c("Nižší než VŠ", "VŠ")

 

# gmodels

library("gmodels")

 

?CrossTable()

Chí-kvadrát

Kontingenční tabulky

# Generate a cross table of gender and education
Gedu_CT_01 <- CrossTable(gedu$Edu, gedu$Gender)

 

# Generate a crosstable for gender and education in which only the results for the chi-square test are included, and the row proportions.
Gedu_CT_02 = CrossTable(gedu$Edu, gedu$Gender, prop.c = FALSE, prop.t = FALSE, chisq  = TRUE, prop.chisq = FALSE)

 

# Generate a cross table of gender and fulltime in SPSS format
Gedu_CT_03 = CrossTable(gedu$Edu, gedu$Gender, format = "SPSS")

Chí-kvadrát

Velikost účinku - phí (dle Phi coefficient, n.d.)

library("psych")

 

Gen = gedu$Gender
Edu2 = gedu$Edu2

 

table_phi = table(Gen, Edu2)

 

phi(table_phi, digits = 2)

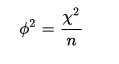
Chí-kvadrát

Velikost účinku - Cramerovo V (dle Cramér's V, n.d.)

library("psych")

 

Gen = gedu$Gender
Edu = gedu$Edu

 

table_CV = table(Gen, Edu)

cramersV(table_CV)

Zdroje

Conway, A. (n.d.) Intro to Statistics with R: Student's T-test. Dostupné online na: https://www.datacamp.com/courses/intro-to-statistics-with-r-students-t-test

 

Cramér's V. (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Cram%C3%A9r%27s_V

Effect size (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Effect_size

 

Pearson's chi-squared test (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test

 

Pearson product-moment correlation coefficient (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient

 

Phi coefficient (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Phi_coefficient

Sampling distribution (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Sampling_distribution

 

Standard error (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Standard_error

Student's t-test (n.d.). In Wikipedia: Staženo dne 10. 10. 2016 z https://en.wikipedia.org/wiki/Student%27s_t-test