Стереометрия. Введение
10 класс
vkrysanov320@gmail.com
version 3.3, 04-09-2025Что такое стереометрия?
Школьный курс геометрии
Стереометрия
Планиметрия
Cтереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве (от др.-греч. στερεός [стереос] — «твёрдый; объёмный, пространственный» + μετρέω [метрео] — «измеряю»).
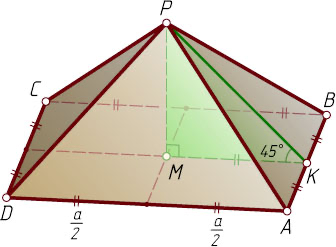
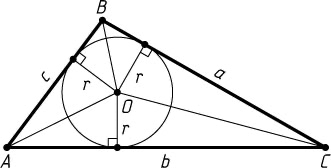
Основные фигуры стереометрии
Точка
Прямая
Плоскость
A
a
\alpha
A, B, C, ...
a, b, c, ..., AB, BC, ...
\alpha, \beta, \gamma, ..., ABC, BCD, ...
\begin{cases}
\\
\\
\\\\\\\\\\\\\\\\\\
\\
\end{cases}
Геометрические тела:
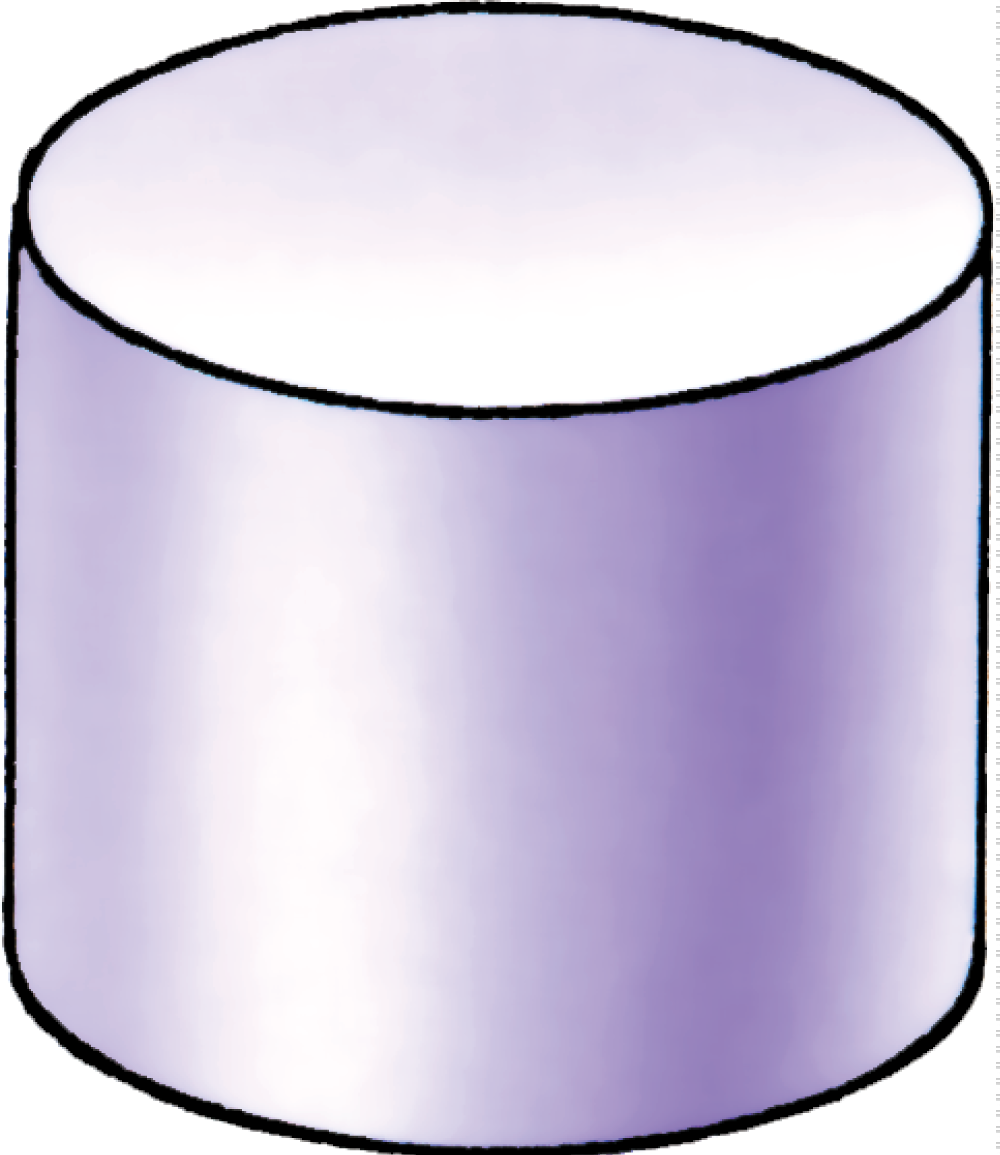
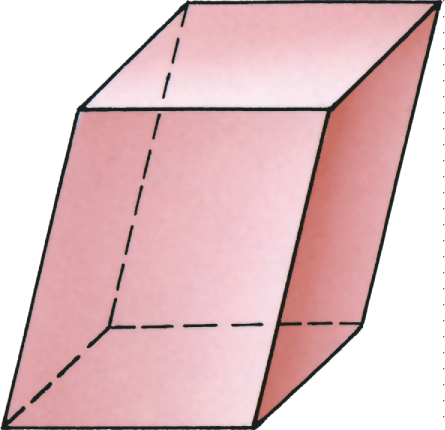
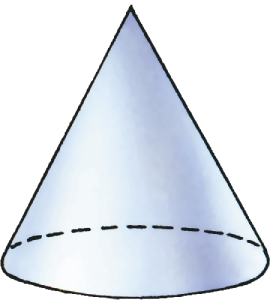
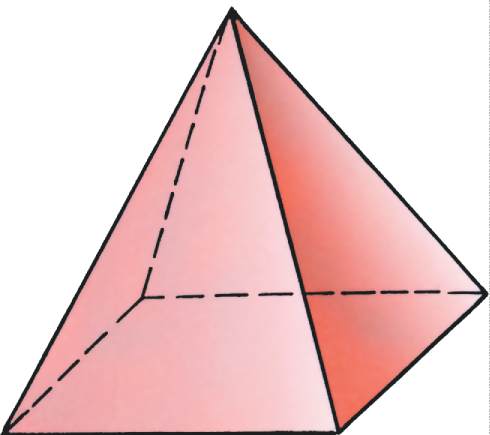
Куб
Шар
Параллелепипед
Цилиндр
Конус
Пирамида
Некоторые понятия стереометрии
Ребро (прямая)
Вершина (точка)
Грань
(плоскость)
\alpha
A
k
B
A \notin \alpha, B \in \alpha
C
k \cap \alpha = C
BC \subset \alpha
\gamma
\beta
\beta \cap \gamma = c
c
пересечение
явл. подмножеством
символы принадлежности
Аксиомы стереометрии
Аксиомы стереометрии (I)
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиомы стереометрии (II)
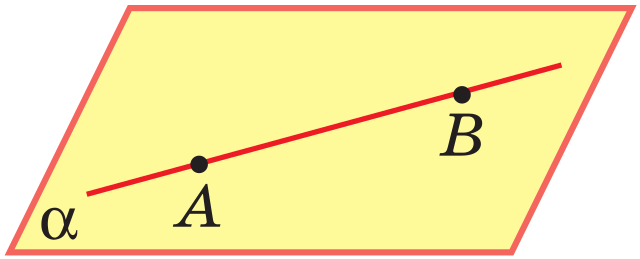
Eсли две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
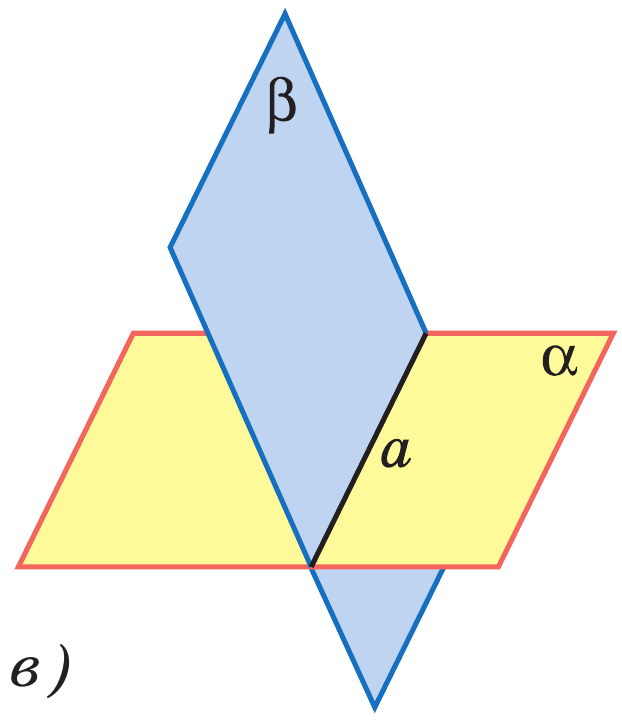
Аксиомы стереометрии (III)
Eсли две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Следствия из аксиом
Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Задачи
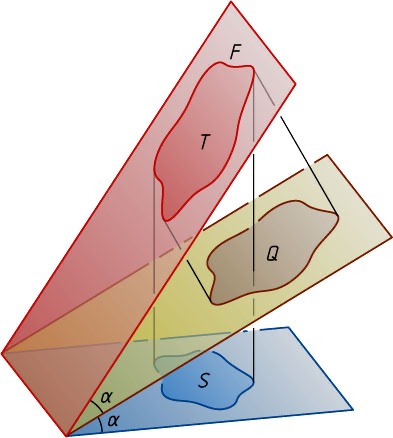
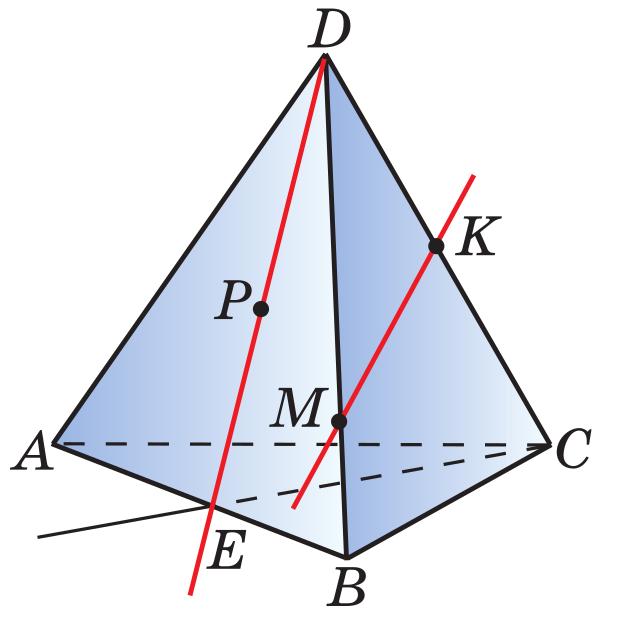
1. По чертежу определить:
а) плоскости, в которых лежат прямые
б) точки пересечения прямой с плоскостью , прямой с плоскостью ;
в) точки, лежащие в плоскостях и
г) прямые, по которым пересекаются плоскости и , и , и .
PE, MK, DB, AB, EC;
DK
ABC
CE
ADP
ADB
DBC;
ABC
DCB
ABD
CDA
ABC
PDC
Задачи (2)
2. Записать символически и сделать чертежи:
а) точка принадлежит плоскости , а точка ей не принадлежит;
б) плоскость проходит через прямую ;
в) прямая пересекает плоскость в точке ;
г) плоскости и пересекаются по прямой ;
д) прямые , и имеют общую точку и не лежат в одной плоскости;
е) прямые и , изображенные на рисунке параллельными, на самом деле не параллельны;
ж) прямые и , изображенные на рисунке пересекающимися, на самом деле не имеют общих точек.
\alpha
T
P
\alpha
k
PT
\alpha
S
\alpha
\beta
k
MA
BC
a
b
c
MA
BC
Задачи (3)
3. Две плоскости имеют две общие точки. Какая фигура является их пересечением? Ответ обосновать.
4. Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.
5. Верно ли утверждение:
а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости;
б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
6. Верно ли, что прямая лежит в плоскости данного треугольника, если она:
а) пересекает две стороны треугольника;
б) проходит через одну из вершин треугольника?
Задачи (4)
7. Могут ли две плоскости иметь:
а) только одну общую точку;
б) только две общие точки;
в) только одну общую прямую?
8. Три прямые проходят через одну точку. Через каждые две из них проведена плоскость. Cколько всего проведено плоскостей?
9. Три прямые попарно пересекаются. Доказать, что они либо лежат в одной плоскости, либо имеют общую точку.
10. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли две другие вершины параллелограмма в плоскости ? Oтвет обоснуйте.
\alpha
\alpha
Задачи (5)
11. Можно ли провести плоскость через четыре произвольные точки пространства? Ответ обосновать.
12. Плоскости и пересекаются по прямой , прямая лежит в плоскости и пересекается с прямой в точке . Доказать, что точка — общая точка плоскостей и .
\alpha
\gamma
k
\alpha
k
C
C
\alpha
\gamma
a
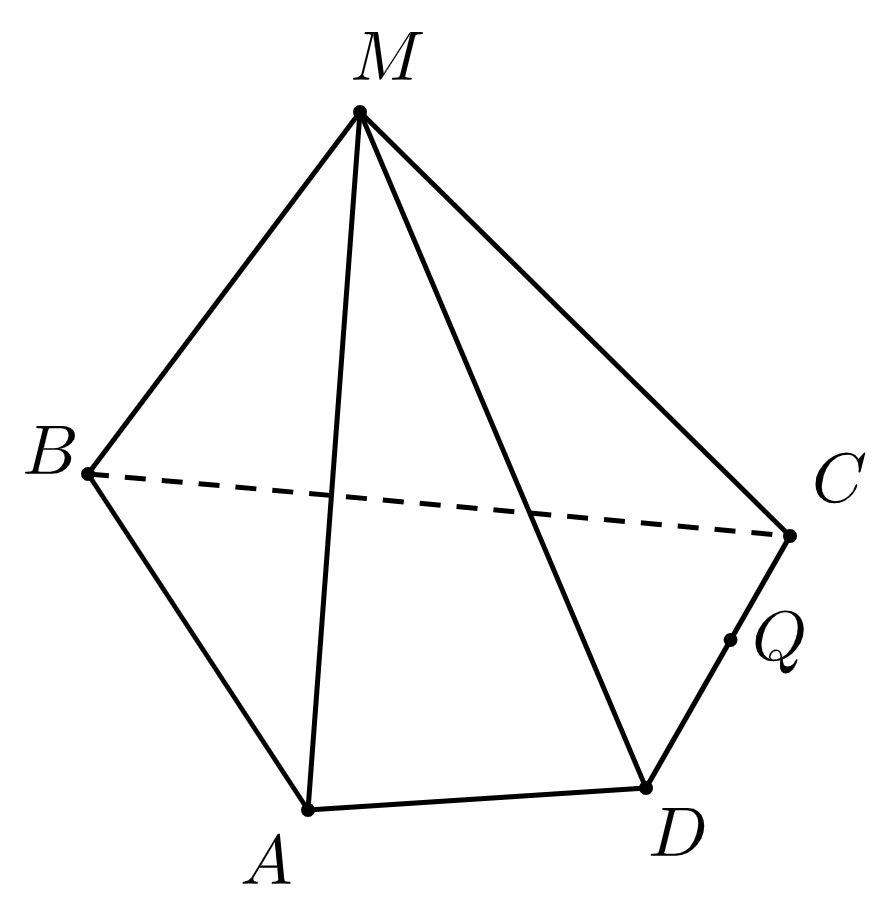
13. Продолжения каких рёбер пирамиды пересекает прямая ?
SABC
MN
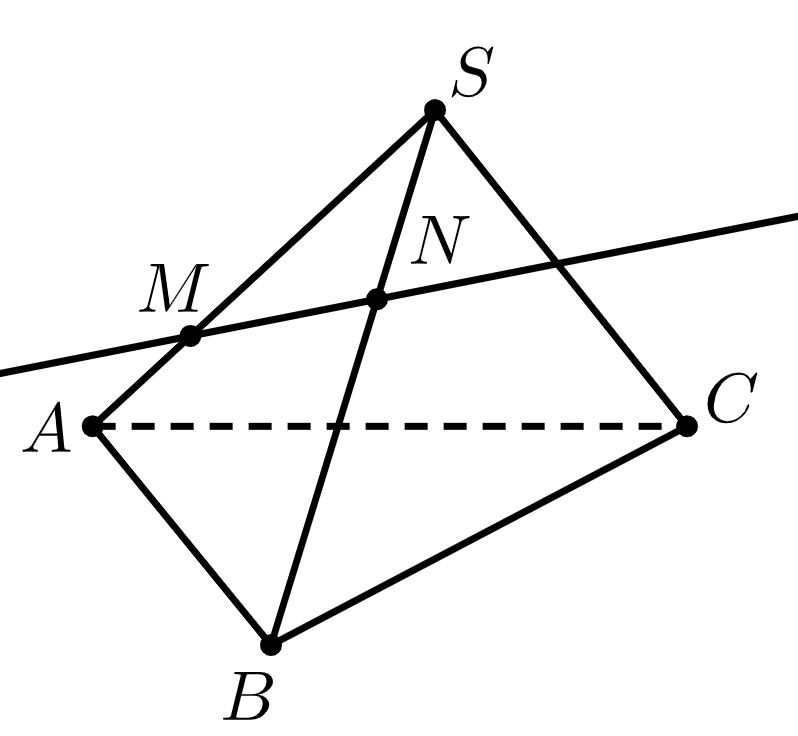
14. Какие из пересечений на рисунке можно считать точками пересечения соответствующих прямых в пространстве?
N, P, E, G
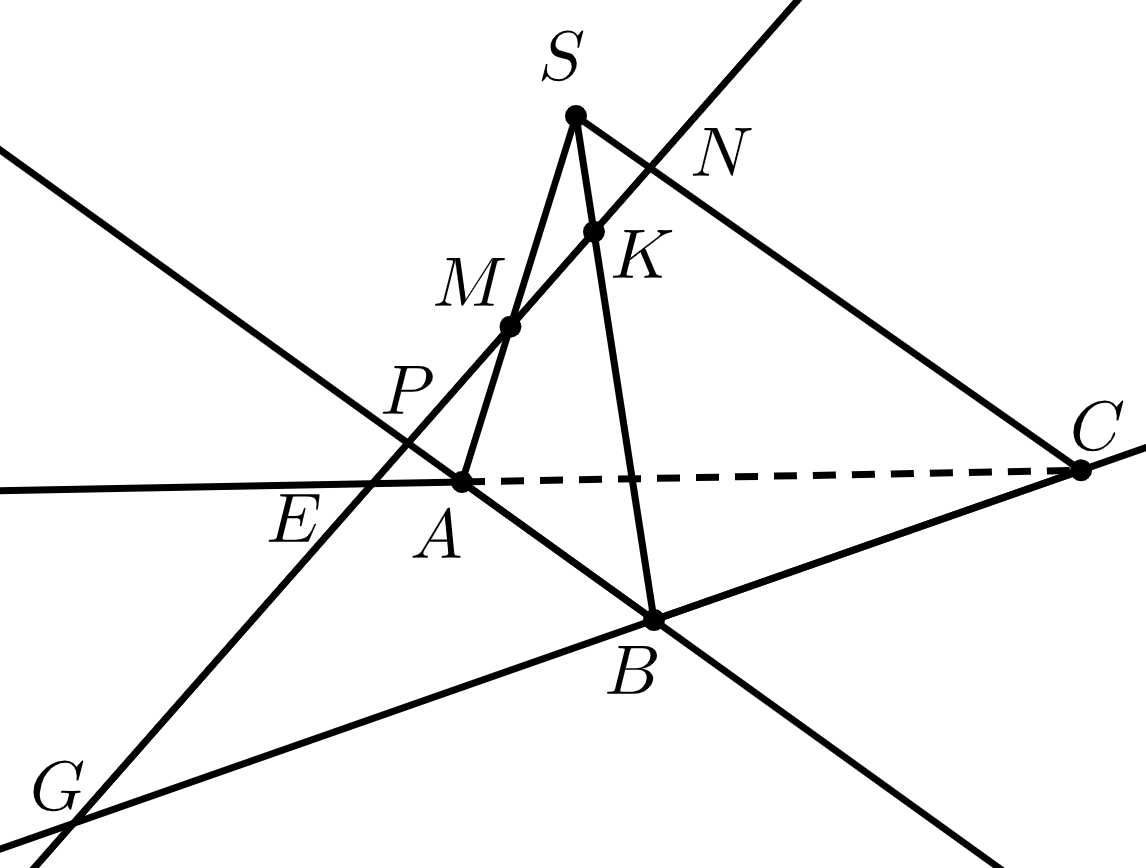
Задачи (6)
15. Построить линии пересечения заданных плоскостей:
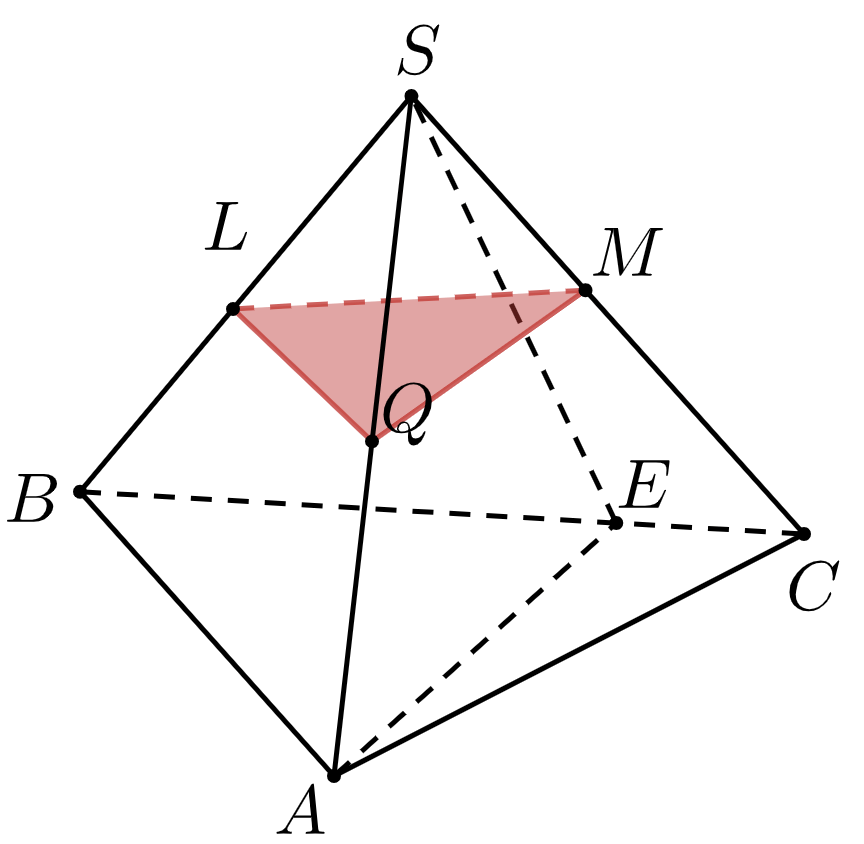
*Для построения линии пересечения двух плоскостей достаточно найти две общие точки этих плоскостей.
MKL \cap ASI
ASL \cap CEK
ASE \cap LQM
Задачи (7)
16. Построить линии пересечения заданных плоскостей:
MAB \cap MCD
MAB \cap MDE
MEA \cap MCB
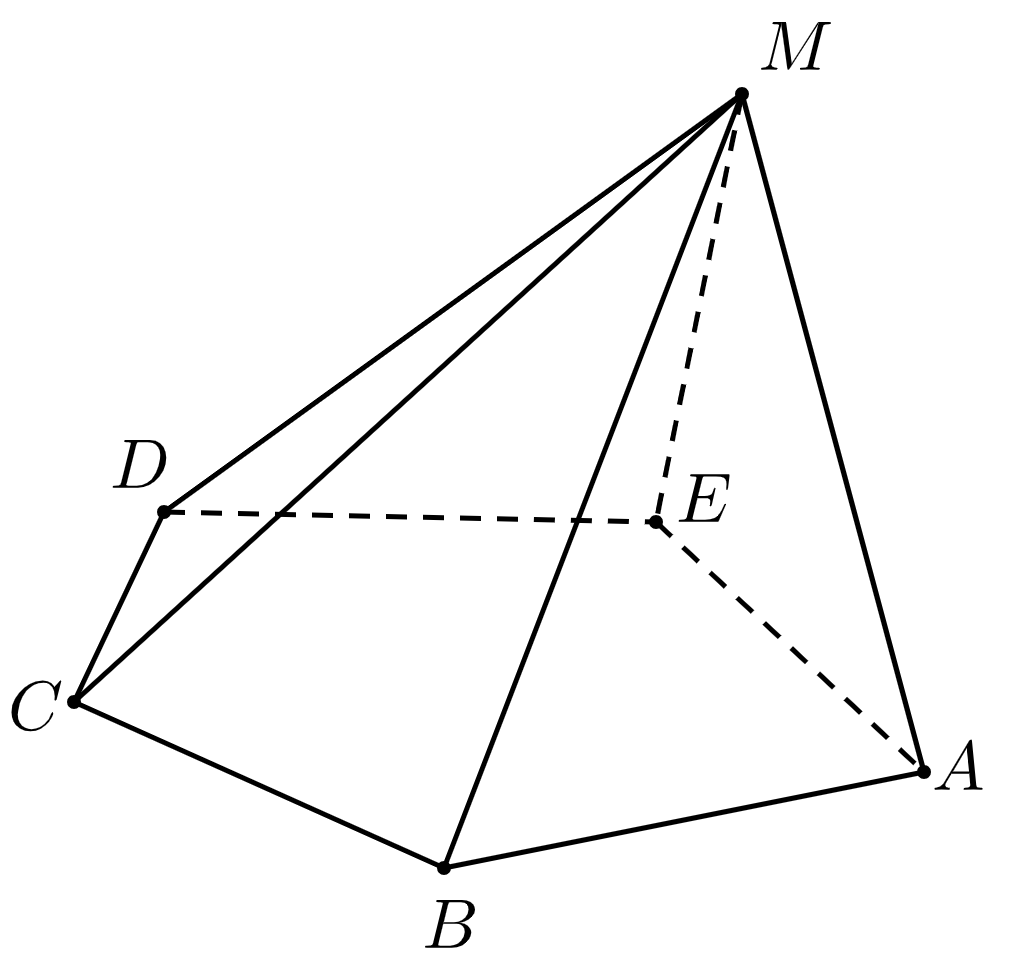
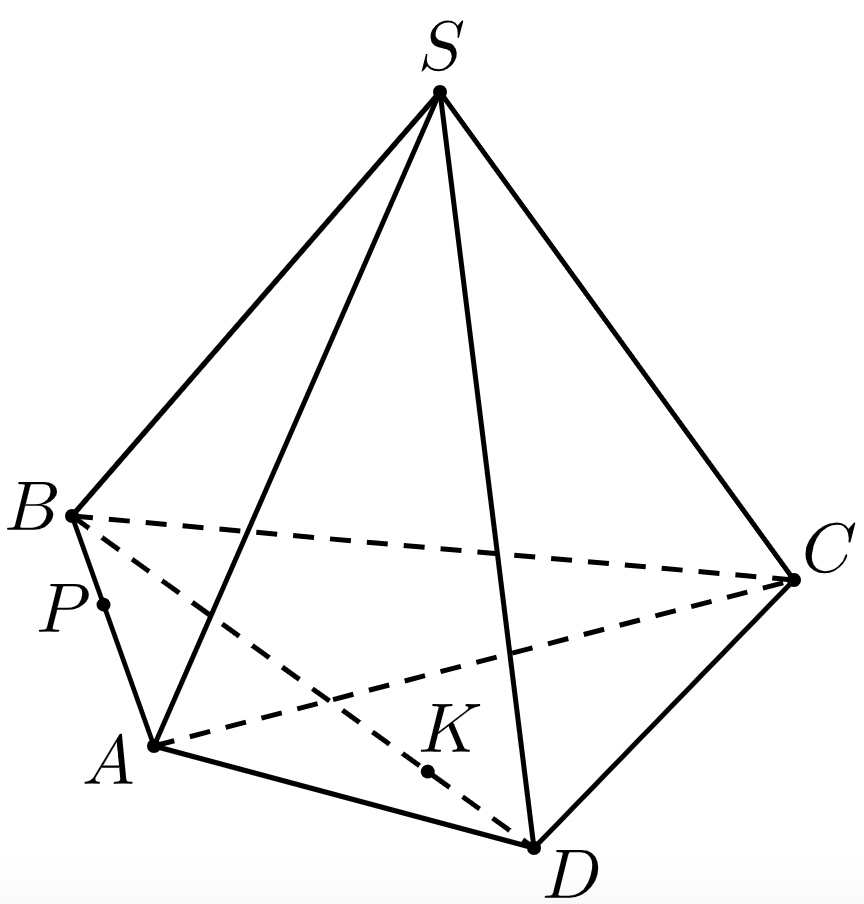
а)
б)
в)
I.
II.
III.
SBD \cap SAC
SCK \cap SAB
SCP \cap SCD
а)
б)
в)
MAQ \cap MCD
MAQ \cap MBC
MDQ \cap MAB
а)
б)
в)
Г0. Стереометрия. Введение
By vkrysanov320
