Задача 5

Создание таблицы

CREATE TABLE table_name (
    column_name1 data_type1 [column_constraint],
    column_name2 data_type2 [column_constraint],
    ...
    [table_constraint]
);

Основные типы данных:

Основные ограничения:

NOT NULL — не пустое значение 

UNIQUE — уникальное значение

SERIAL PRIMARY KEY — первичный ключ

FOREIGN KEY — внешний ключ

INTEGER — целые числа

REAL — числа с плавающей точкой

TEXT — строки

VARCHAR(n) — строка из n символов

BOOLEAN — булевский тип

DATE — дата

TIME — время

Ограничения таблицы

Создание таблицы. Пример

CREATE TABLE users (
    user_id SERIAL PRIMARY KEY,
    username VARCHAR(50) UNIQUE NOT NULL,
    email VARCHAR(255) UNIQUE NOT NULL
);
CREATE TABLE posts (
    post_id SERIAL PRIMARY KEY,
    title VARCHAR(200) NOT NULL,
    content TEXT NOT NULL,
    user_id INTEGER NOT NULL,
    	FOREIGN KEY (user_id) REFERENCES users(user_id)
);
users
user_id (PK)
username
email
posts
post_id (PK)
title
content
user_id (FK)

1

М

Запросы

SELECT [ ALL | DISTINCT [ ON ( expression [, ...] ) ] ]
[ FROM from_item [, ...] ]
[ WHERE condition ]
[ GROUP BY expression [, ...] ]
[ HAVING condition [, ...] ]
[ { UNION | INTERSECT | EXCEPT } [ ALL | DISTINCT ] select ]
[ ORDER BY expression [ ASC | DESC]
[ NULLS { FIRST | LAST } ] [, ...] ]
[ LIMIT { count | ALL } ]
[ OFFSET start [ ROW | ROWS ] ];

LIMIT

SELECT ... FROM ...
LIMIT n;

LIMIT ограничивает количество строк, возвращаемых запросом. Он всегда выполняется после всех других операций:

SELECT user_id, username, email FROM users
LIMIT 3;

Примеры:

WHERE

SELECT ... FROM ...
WHERE condition;

WHERE фильтрует строки перед их обработкой. Он определяет, какие строки будут включены в результат запроса:

SELECT user_id, username, email FROM users
WHERE username = 'alex';

SELECT title, content FROM posts
WHERE user_id = 1;

SELECT username, email FROM users
WHERE user_id BETWEEN 1 AND 3 AND username != 'john';

SELECT username, email FROM users
WHERE user_id IN (1, 3);

Примеры:

ORDER BY

SELECT user_id, username, email
FROM users
ORDER BY username ASC;  


SELECT user_id, username, email
FROM users
ORDER BY username DESC;

Сортировка таблицы по

 

SELECT ... FROM ...
ORDER BY column_name ASC;

SELECT ... FROM ...
ORDER BY column_name DESC;

возрастанию:

убыванию:

Примеры:

GROUP BY

SELECT user_id, COUNT(*) as post_count FROM posts
GROUP BY user_id;

GROUP BY в SQL работает, собирая строки с одинаковыми значениями в одну группу, чтобы затем выполнить агрегатные функции (например, COUNT, SUM, AVG) над каждой группой отдельно. Результатом запроса становится одна строка для каждой уникальной комбинации значений в столбцах, указанных в GROUP BY. 

SELECT ... FROM ...
GROUP BY ...;

Примеры:

HAVING

SELECT user_id, COUNT(*) as post_count FROM posts
GROUP BY user_id
HAVING COUNT(*) > 1;

С помощью ключевого слова HAVING мы можем задать условия на строки выборки после группировки данных.

SELECT ... FROM ...
GROUP BY ...
HAVING ...

Примеры:

COUNT() —  подсчет кол-ва строк

SUM() — сумма числовых значений строк

MAX() — наибольше значение в выборке

MIN() — наименьшее значение в выборке

Основные агрегатные функции:

как правило используется с агрегатными функциями

Запросы

SELECT posts.title, posts.content FROM posts
JOIN users ON posts.user_id = users.user_id
WHERE users.username = 'Иван';

Задача 8

Распределения

В теории вероятностей выделяют два фундаментальных класса распределений: дискретные и непрерывные.

Непрерывные распределения моделируют случайные величины, способные принимать любые значения в определённом интервале.

Дискретные распределения описывают случайные величины, которые принимают отдельные, изолированные значения.

  • Все значения из конечного множества равновероятны

Дискретные распределения (1)

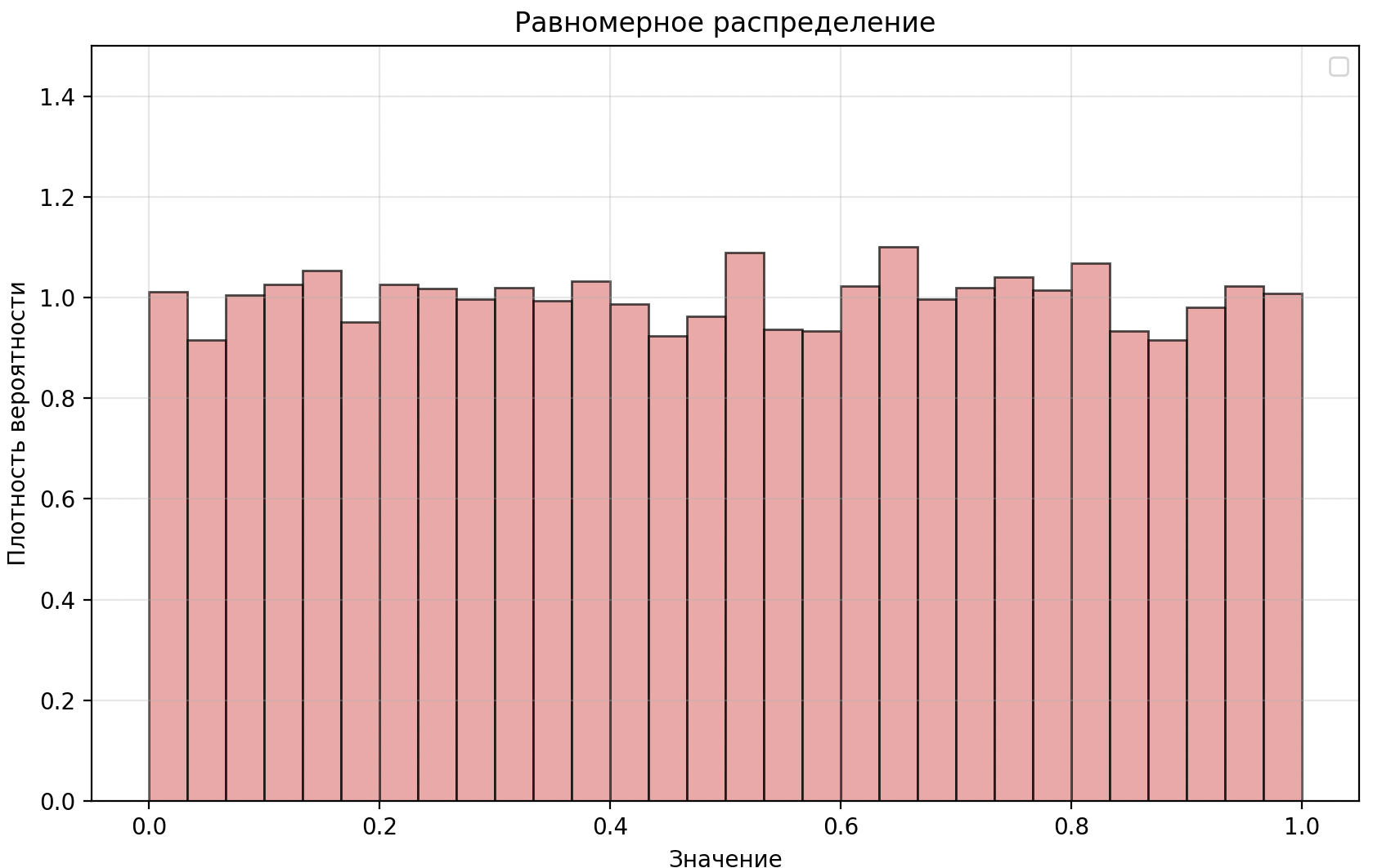
Равномерное распределение

  • Все значения одинаковой высоты
a
b

Дискретные распределения (2)

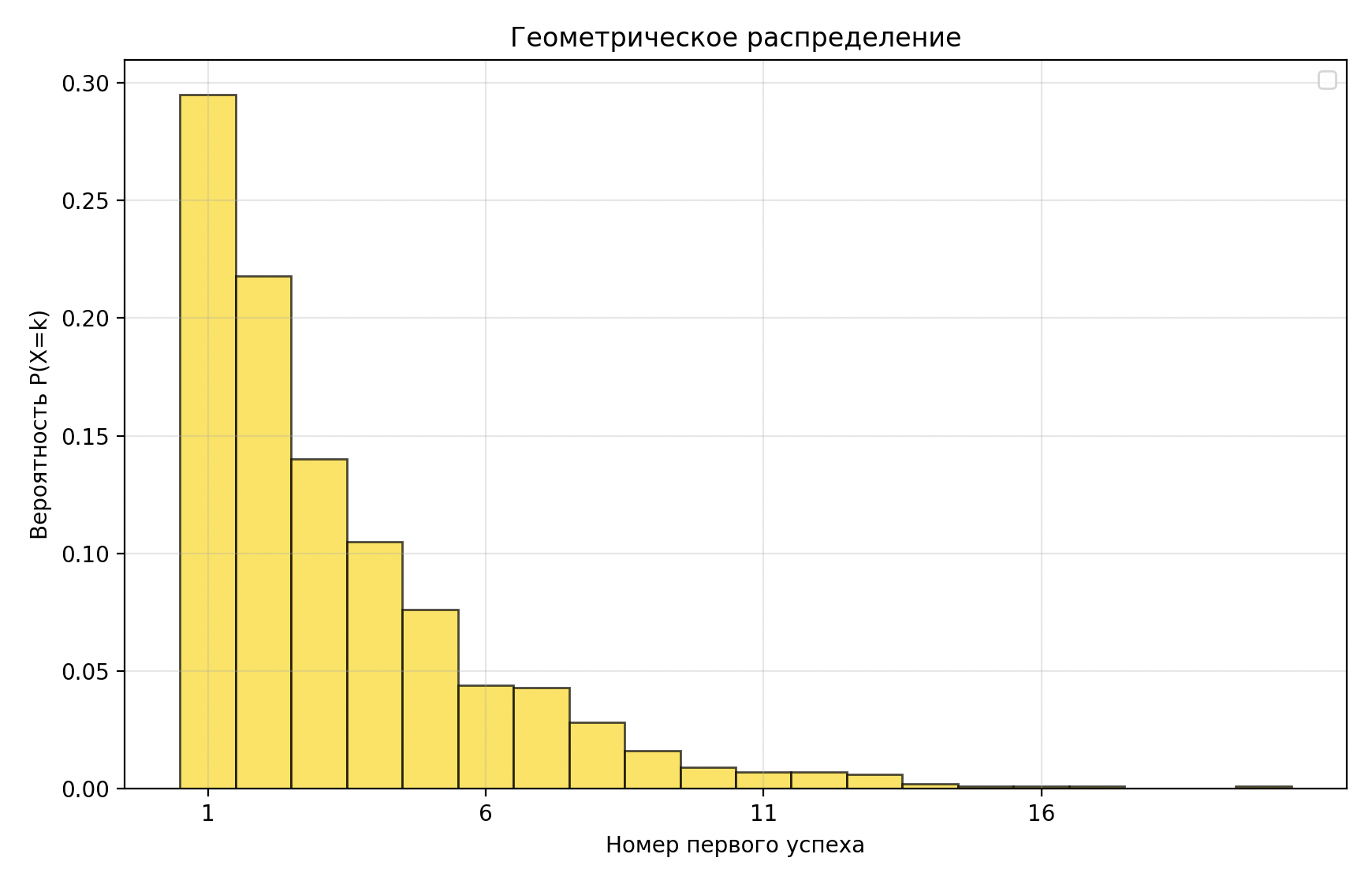
Геометрическое распределение

  • Описывает, сколько требуется попыток для достижения первого успеха.

  • Начинается с 1.
  • Форма скатывающейся горки

Примеры:

• Число бросков монетки до первого орла
• Количество попыток до первого попадания в цель
• Число тестов до обнаружения первого бага в программе
• Количество звонков до первой продажи
• Число попыток до первого выигрыша в казино

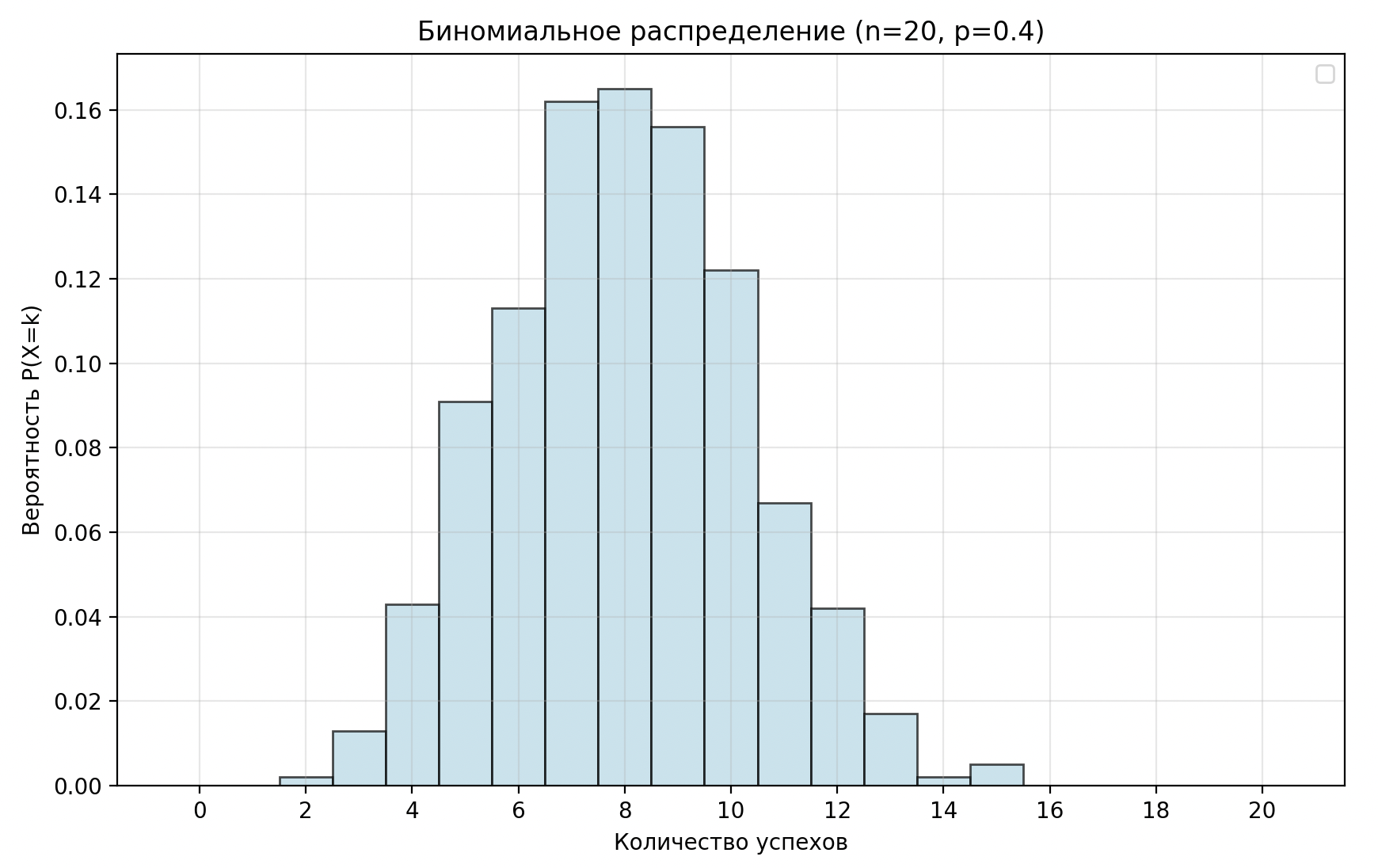
Дискретные распределения (3-4)

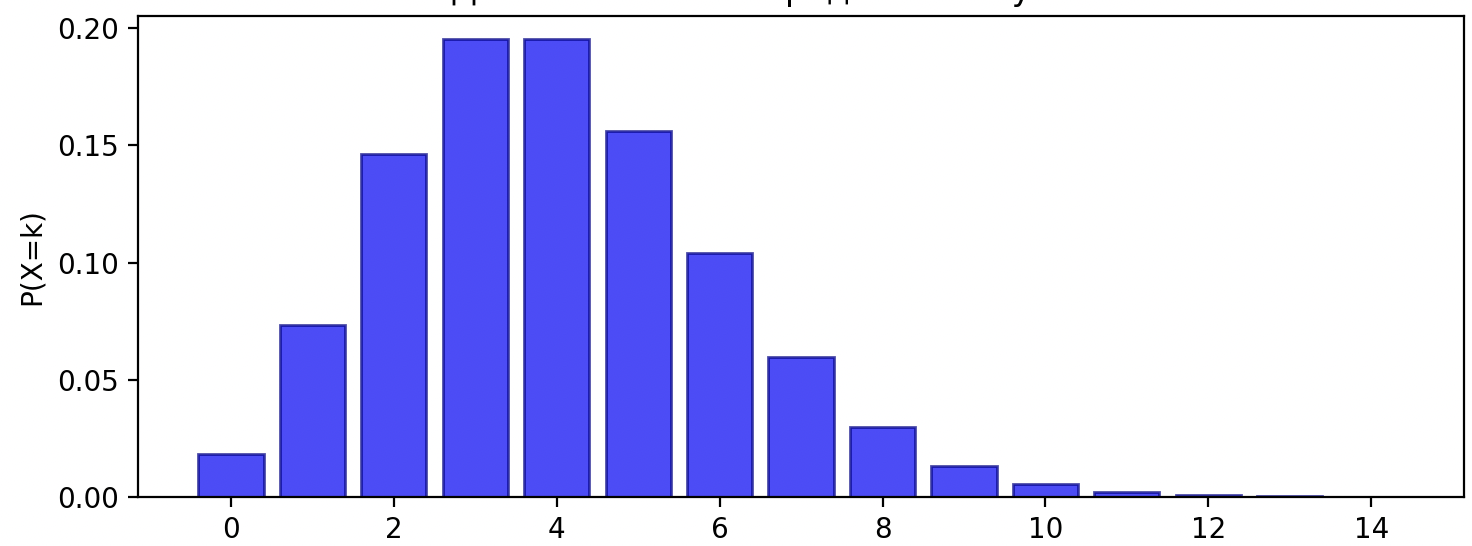
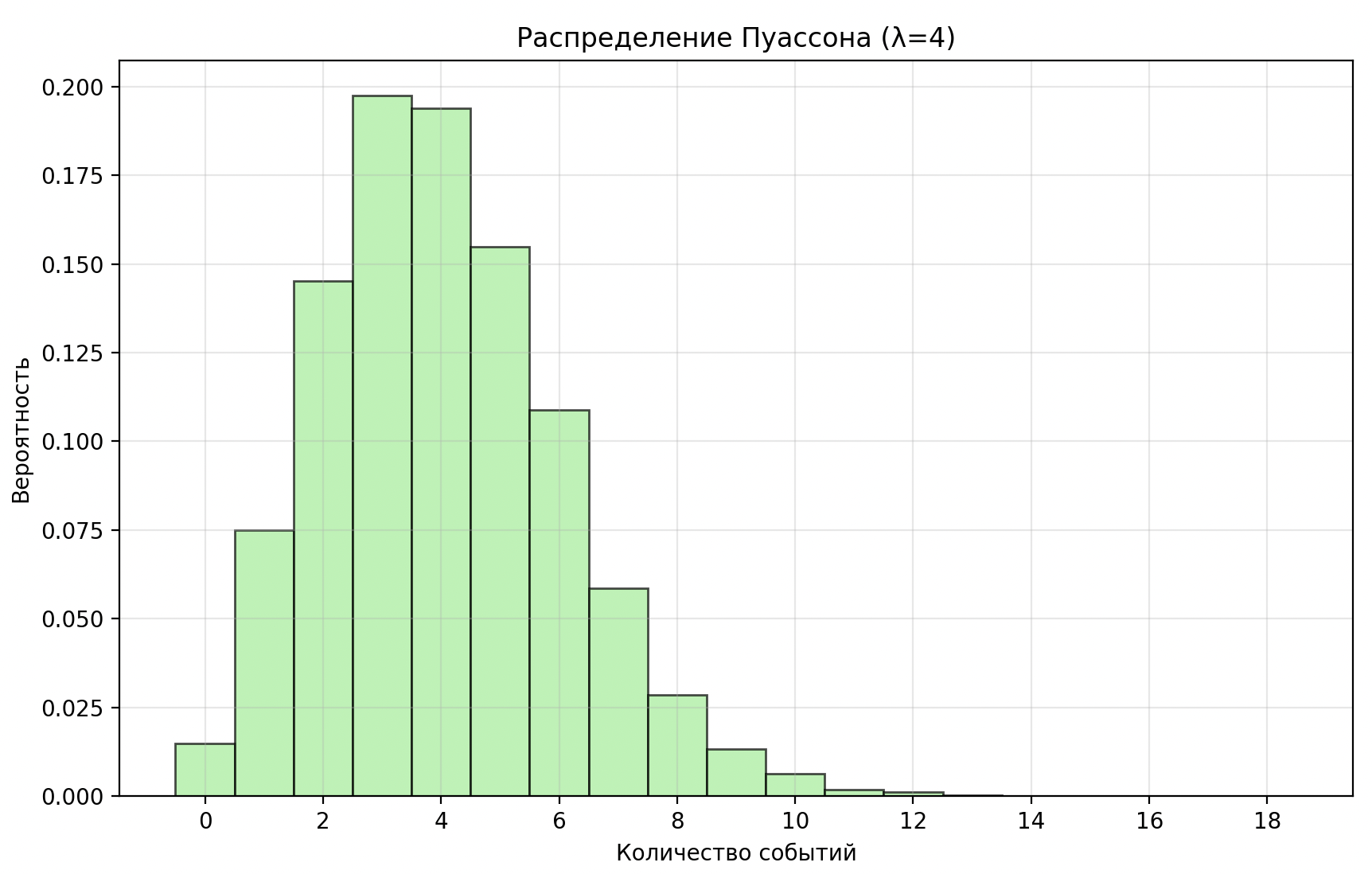
Распределение Пуассона. Биномиальное распределение

Пуассона Биномиальное
Что считаем? События за время Успехи в n попытках
Параметры λ n, p
Диапазон 0, 1, 2, ... (без ограничения) 0, 1, 2, ..., n
Пример 5 клиентов за час 3 орла из 10 бросков

  • Описывает,  сколько раз произойдет определенное событие за фиксированный период времени или в определенном пространстве.

  • Описывает,  моделирование числа успешных исходов в серии независимых испытаний с двумя возможными исходами: успех или неудача.

  • куполообразная форма
  • ограниченные диапазон
  • Скошенная вправо горка
  • Длинный правый хвост — постепенно спадает до 0
  • В нуле есть значения

    — количество испытаний

    — это среднее количество событий за фиксированный интервал времени или пространства.

\lambda
n
\mu
p = \frac{\mu}{n}

Дискретные распределения (3-4)

Распределение Пуассона. Биномиальное распределение. Примеры

Примеры:

• Количество клиентов в магазине за 15 минут

• Число звонков в кол-центр за час
• Число аварий на дороге за день
• Количество опечаток на странице текста
• Число землетрясений в регионе за год
• Количество посетителей сайта в минуту

​

Примеры:

• Число правильных ответов в тесте из 20 вопросов

• Количество выигрышных лотерейных билетов из 100

• Число успешных продаж из 50 холодных звонков

• Количество дефектных изделий в партии из 1000

• Число попаданий в баскетбольную корзину из 10 бросков

• Количество орлов при 100 подбрасываниях монетки

Распределение Пуассона

Биномиальное распределение

Непрерывные распределения (1)

Равномерное распределение

  • Постоянная высота.
  • Резкие границы.
  • Прямоугольная форма.

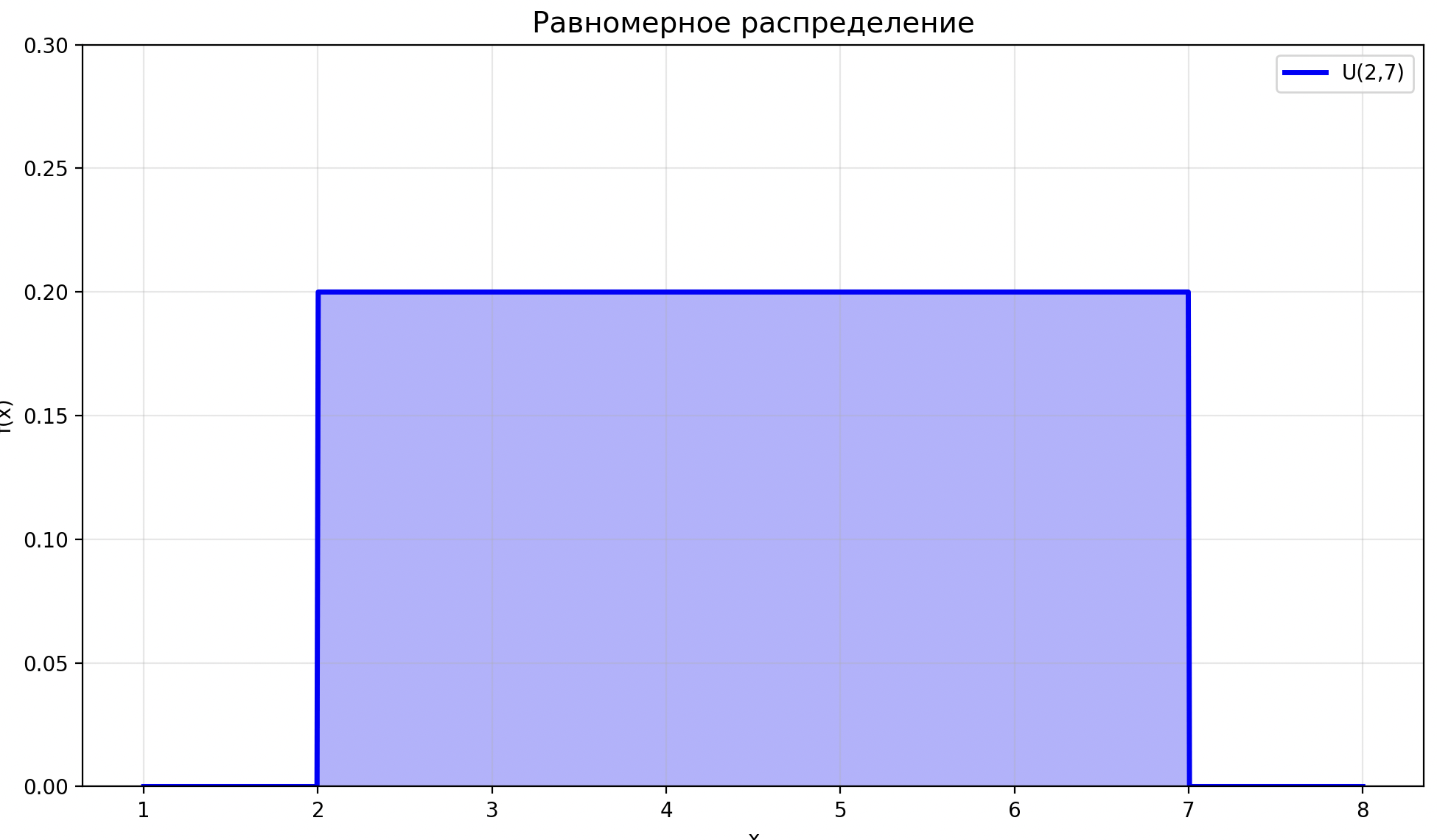
  • Все значения из конечного множества равновероятны

a
b
h = \frac{1}{b-a}

Примеры:

• Случайное число от 1 до 100
• Результат броска игрального кубика
• Время ожидания автобуса (если ходит по расписанию)
• Выбор случайного человека из группы
• Координата точки на отрезке

Непрерывные распределения (2)

Экспоненциальное распределение

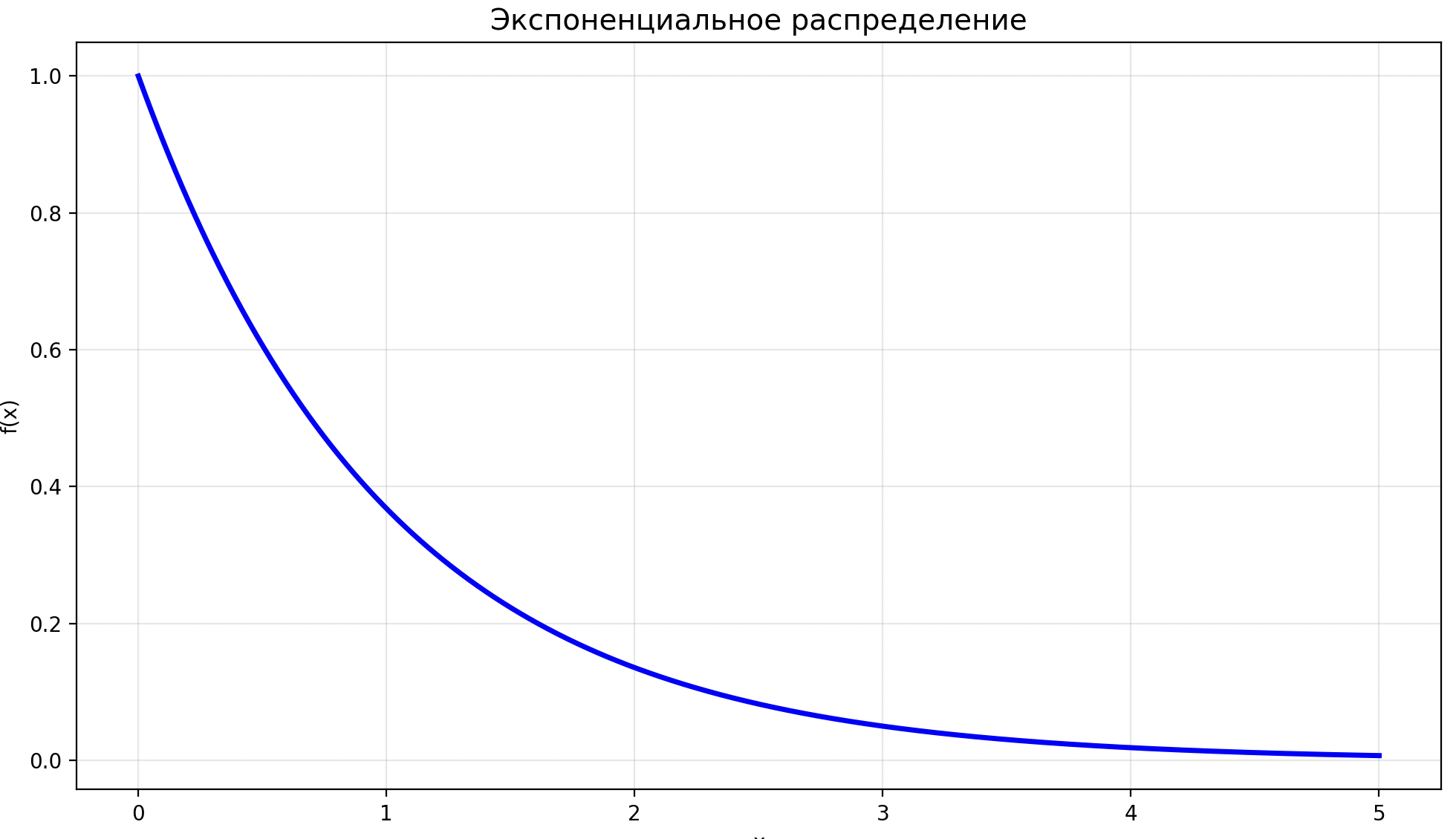
  • Резкое убывание.
  • Длинный «хвост» справа.
  • Симметрия отсутствует.
  • Начинается с максимума.
  • Форма гауссова распределения, в которой данные описывают время между событиями, которые происходят с постоянным средним интервалом.
\lambda

Примеры:

• Время между звонками в кол-центр
• Длительность телефонных разговоров
• Время до отказа электронного компонента
• Длительность обслуживания клиента в банке
• Длительность безработицы

Непрерывные распределения (3)

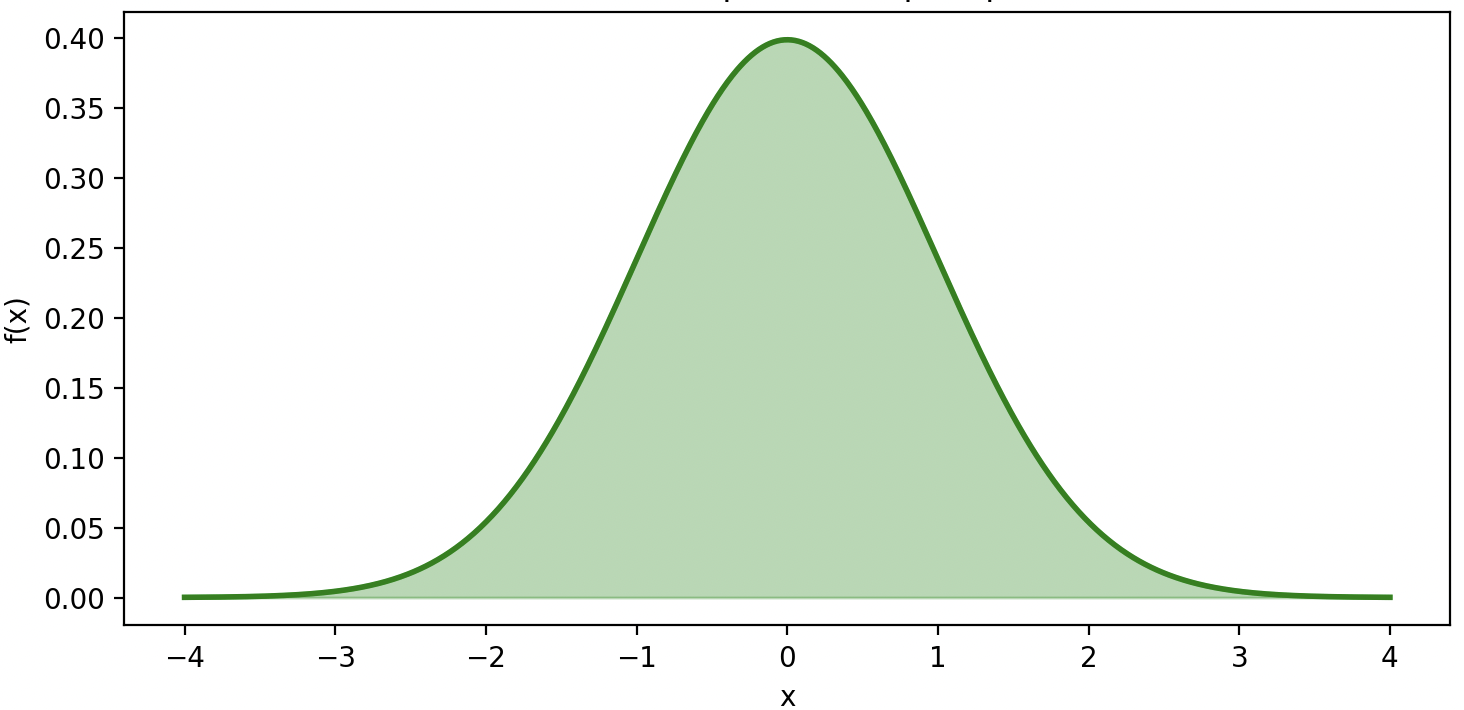
Нормальное (Гауссово) распределение

  • куполообразная форма.

  •     — среднее значение (определяет центр распределения).

  •     — стандартное отклонение (определяет ширину распределения)

\mu = 5
\mu
\sigma

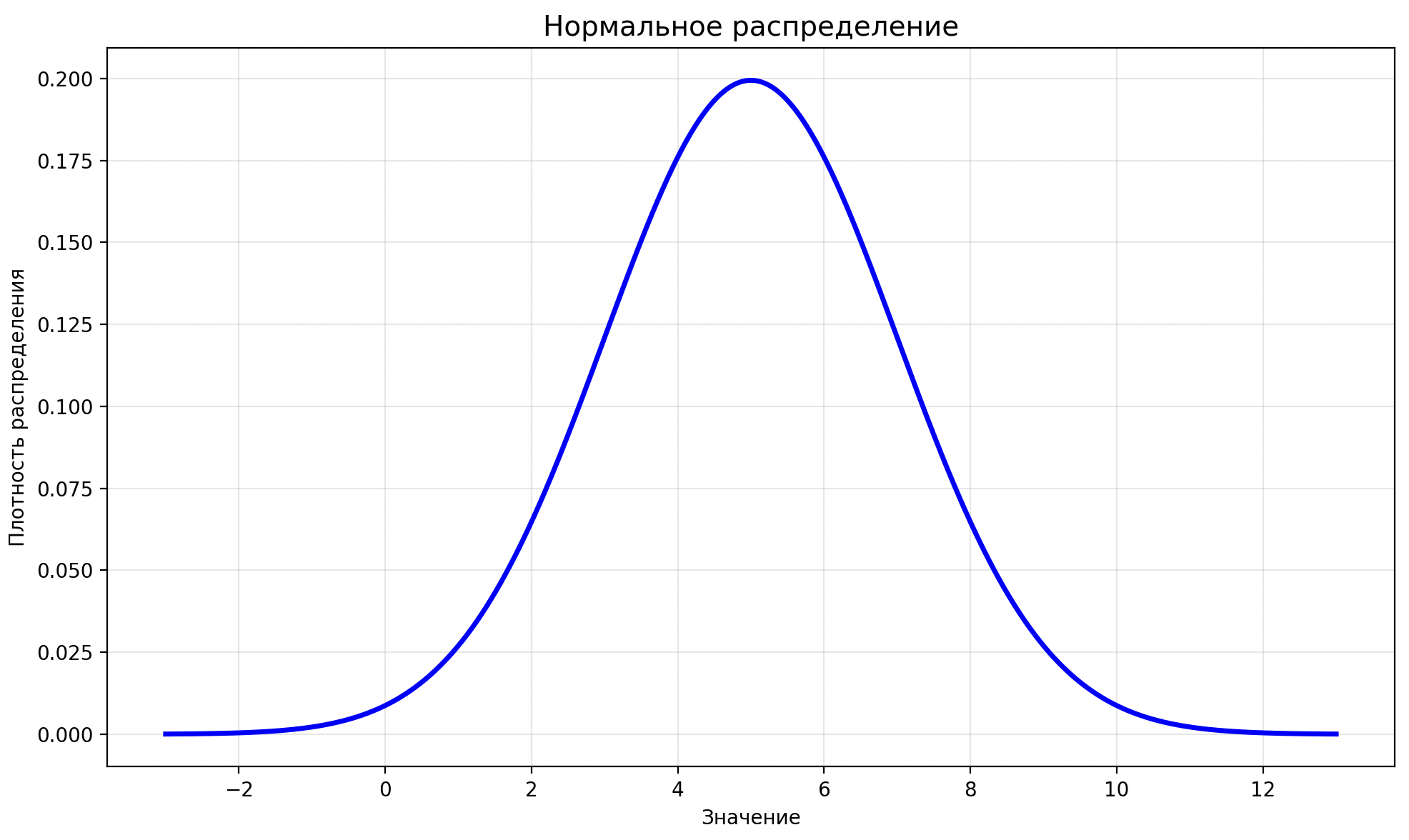
Медиана, мода, среднее совпадают

*Для нахождения    необходимо найти точки перегиба — они всегда находятся точно на расстоянии    от    .  

Точка перегиба

\sigma = 2
\sigma
\sigma
\mu

Примеры:

• Рост взрослых людей в популяции
• Размер обуви в магазине  
• Результаты IQ-тестов
• Погрешности измерений
• Вес новорожденных детей
• Время реакции человека

Copy of Особенности изучения профильной математики в ИТ-классе

By vkrysanov320

Made with Slides.com

Copy of Особенности изучения профильной математики в ИТ-классе

  • 96

More from vkrysanov320

  • Особенности изучения профильной математики в ИТ-классе
    vkrysanov320
    217
  • 5. Основы языка программирования Python. Строки
    vkrysanov320
    481