А0. Теория вероятностей

Если космос располагает безграничным запасом времени, это не просто означает, что может произойти всё, что угодно. Это означает, что всё когда-нибудь действительно произойдет.

Эрленд Лу

Что такое теория вероятностей?

Теория вероятностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.

* При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы. Т.е. теория вероятностей рассматривает не сами реальные явления, а их упрощенные схемы — математические модели.

Прогнозирование временных рядов

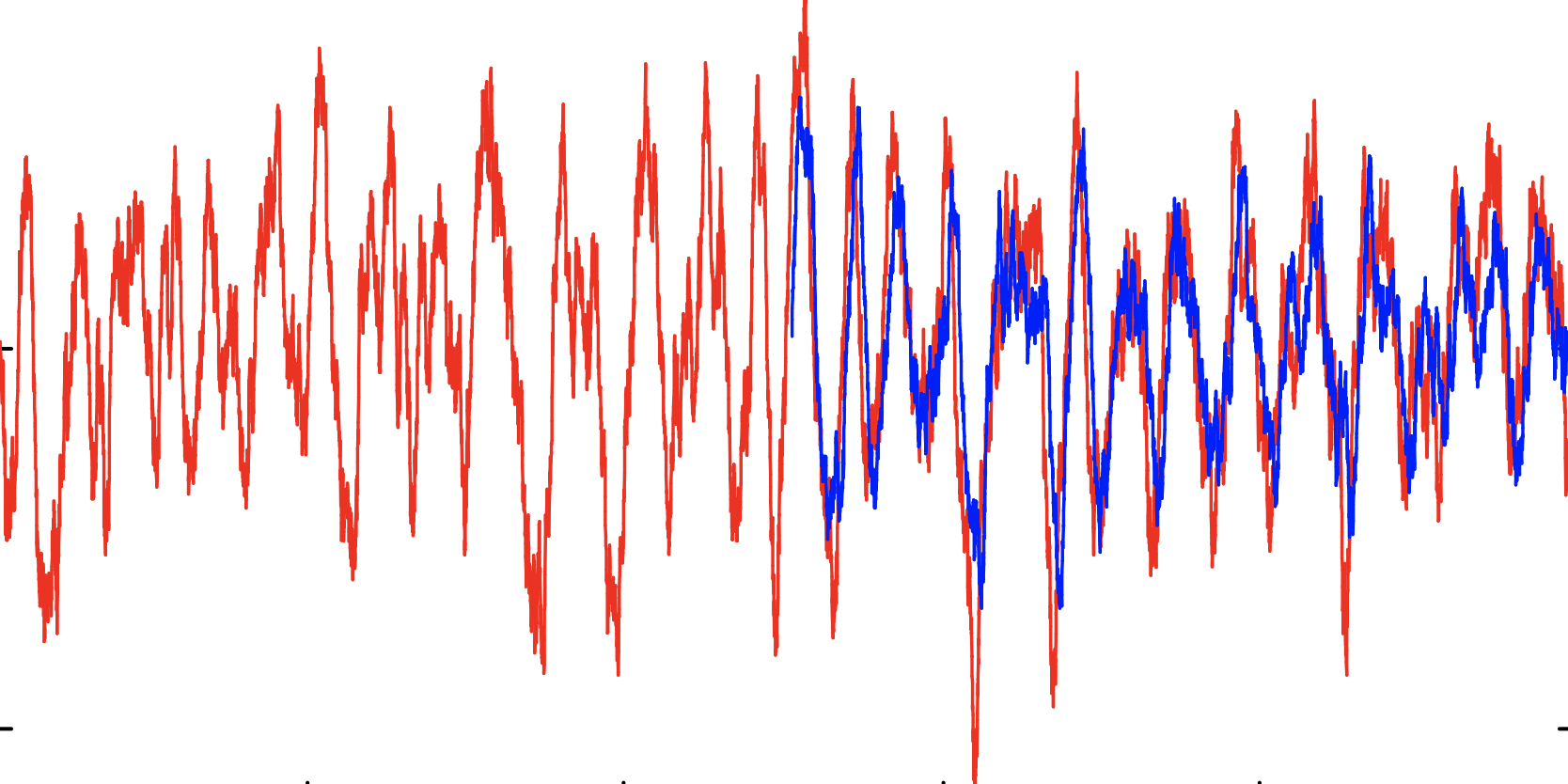
— Реальные значения

— Прогноз

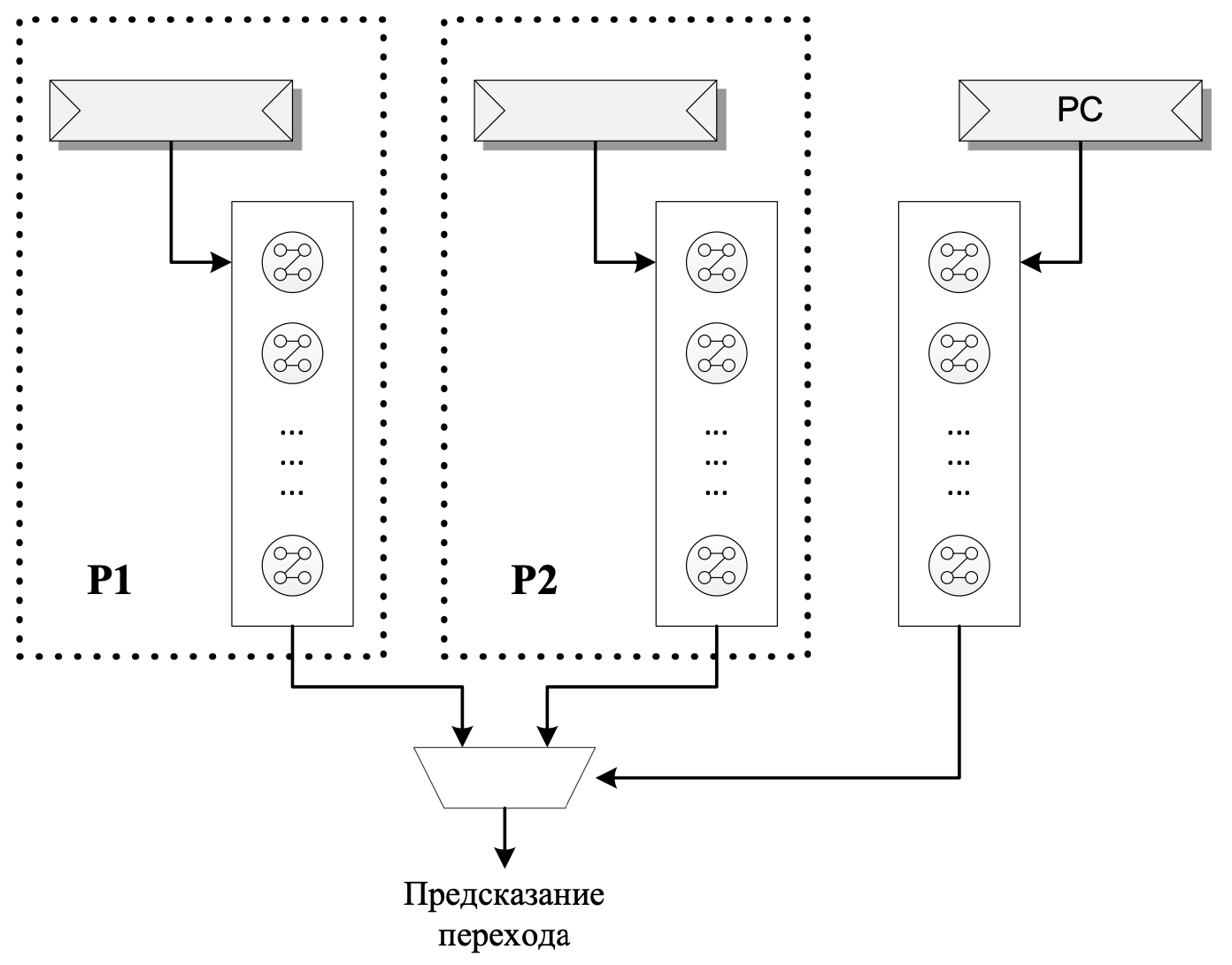
Предсказание переходов в процессорах

Биология

События

Событие — любое явление, которое может произойти или не произойти в результате опыта.

достоверное событие

событие, которое всегда происходит при проведении опыта.

случайное событие

событие, которое может либо произойти, либо не произойти.

невозможное событие

событие, которое в результате опыта произойти не может.

P(A) = 1

P(A) = 0

0 \le P(A) \le 1

Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события.

События обозначают большими латинскими буквами, либо теми же буквами с подстрочными индексами:

A, B, C, ..., A_0, G_T, R_{tf}

Примеры:

A_O

— в результате броска монеты выпадет «орёл».
— в результате броска игральной кости (кубика) выпадет 5 очков.

и т.д.

A_5

* Исключение составляет буква , которая зарезервирована под другие нужды.

P

Пространство исходов — это множество всех исходов. Оно описывает все возможные варианты того, что может случиться в результате эксперимента. Обозначается буквой .

Чаще всего нас интересуют не отдельные исходы, а целые группы исходов. Иначе говоря, мы рассматриваем подмножества множества .

Пространство исходов. Группы событий

\Omega

Примеры:

Подбрасывается монета. Элементарные события: О, Р.
Монета подбрасывается дважды. Элементарные события: ОО, ОР, РО, РР.

О

Р

\Omega = \{О, Р\}

\Omega = \{ОО, ОР, РО, РР\}

ОО

ОР

РР

РО

\Omega

Например, событие можно назвать «первый бросок был решкой».

а событие — «выпала хотя бы одна решка».

\{ОО, ОР\}

\{РР, ОР, РО\}

P(\Omega) = 1

Взаимосвязь событий

Равновероятные события

Равновероятные события — это такие события, которые имеют одинаковые возможности для их появления.

P(\omega_i) = \frac{1}{N}

всего — событий

N

Примеры:

Появление орла или решки при подбрасывание монеты;
Появление какого-либо варианта при одном бросании игральной кости;
Появление какого-либо варианта при вытягивании карты из колоды.

\Omega

Далеко не во всех случайных экспериментах элементарные исходы равновероятны!

* Если у монеты или кубика смещен центр тяжести, то гораздо чаще будут выпадать вполне определённые грани, и в таком случае события с подбрасыванием монеты или кубика уже будут неравновероятными.

Совместные и несовместные события

События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий.

События называют совместными, если в одном и том же испытании появление одного из событий не исключает появление других событий.

Примеры: идет дождь и идет снег, человек ест и человек читает, число целое и четное;

Примеры: день и ночь, человек читает и человек спит, число иррациональное и четное.

U

A

B

совместные события

U

A

B

несовместные события

Противоположные события

Событие противоположно событию , если состоит из тех исходов , в которых нет в .

A

\overline{A}

A

\Omega

A

\Omega

Свойства:

● события и не могут произойти одновременно;
● события и и образуют всё пространство исходов ( ).

\overline{A}

A

\Omega

Примеры:

сдача и несдача экзамена студентом;
день и ночь;
выпала единица и выпало что угодно, кроме единицы (2, 3, 4, 5, 6), в результате броска игрального кубика.

P(\overline{A}) = 1 - P(A)

P(\Omega) = P(A) + P(\overline{A}) \Rightarrow

1

Зависимые и независимые события

Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого. В противном случае (появление одного события изменяет вероятность появления другого) события называются зависимыми.

Как определить зависимость / независимость событий?

Иногда об этом прямо сказано в условии задачи, но чаще приходится проводить самостоятельный анализ. Какого-то однозначного ориентира тут нет, и факт зависимости либо независимости событий вытекает из естественных логических рассуждений.

Примеры:

Подбрасывание двух монет: «появление герба на первой монете» и «появление герба на второй монете» является независимыми событиями.
Вытаскивание шаров из урны: в урне 2 белых шара и один черный; два человека вынимают из урны по одному шару; очевидно, что первое вытаскивание повлияет на результат второго.

Примеры задач на классическое определение вероятности

Элементарные задачи

1. В кармане у Миши было четыре конфеты  — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».

Решение: Задача на классическое определение вероятности:

\Rightarrow P(A) = \frac{1}{4} = 0{,}25.

число подходящих: 1

общее количество исходов: 4

P(A) = 1 - P(\overline{A}) = 1 - \frac{3}{60} = 0{,}05.

Решение:

2. На экзамен вынесено 60 вопросов, Тимошка не выучил 3 из них. Найти вероятность того, что ему попадется невыученный вопрос.

3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

ОО

ОР

РО

ОО

Решение: Переберем варианты и применим классический подход:

\begin{cases} \\ \\ \end{cases}

4 варианта, но подходит только 2

\Rightarrow P(A) = \frac{2}{4} = \frac{1}{2} = 0{,}5.

Задачи на жребьевку

1. В соревновании по биатлону участвуют спортсмены из 25 стран, одна из которых ― Россия. Всего на старт вышло 60 участников, из которых 6 ― из России. Порядок старта определяется жребием, стартуют спортсмены друг за другом. Какова вероятность того, что десятым стартовал спортсмен из России?

Решение: Номер выступления не имеет никакой роли, т.к. речь идет о жеребьёвке

\Rightarrow P(A) = \frac{6}{60} = 0{,}1.

2. На рок-фестивале выступают группы  — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлить до сотых.

...Ш...Н...Д...

...Ш...Д...Н...

...Д...Ш...Н...

...Д...Н...Ш...

...Н...Д...Ш...

...Н...Ш...Д...

Решение: Рассмотрим все возможные случаи выступления:

\begin{cases} \\ \\ \\ \end{cases}

6 вариантов, но подходит только 2

\Rightarrow P(A) = \frac{2}{6} = \frac{1}{3} = 0{,}(3) \approx 0{,}33.

Задачи с числовыми осями

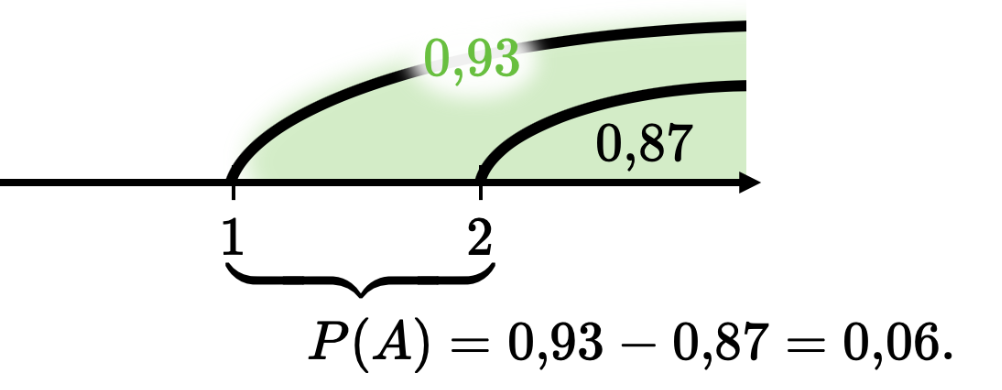
1. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение: Лучше всего рассмотреть графическое решение:

P(A) = 0{,}93 - 0{,}87 = 0{,}06.

2. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.

P(A) = 0{,}82 - 0{,}51 = 0{,}31.

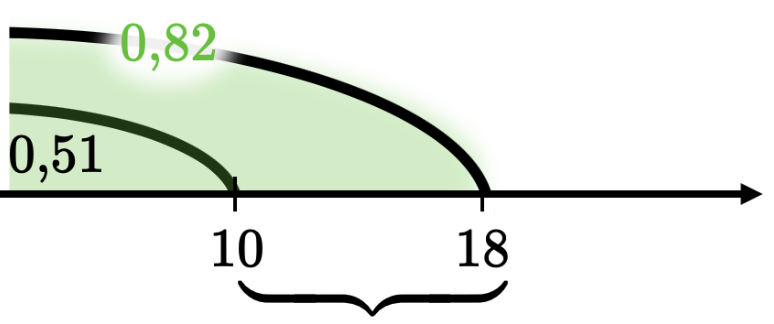
Решение: Аналогично предыдущей задаче:

Задачи «в среднем»

1. Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.

2. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Решение: В среднем без дефектов выпускают 92 сумки из каждых 100:

Решение: По условию из любых 100 + 8  =  108 сумок в среднем 100 качественных сумок. Значит, вероятность того, что купленная сумка окажется качественной, равна:

\Rightarrow P(A) = \frac{92}{100} = 0{,}92.

P(A) = \frac{100}{108} = 0{,}925925... \approx 0{,}93.

обратите внимание на формулировки!

Задачи на классическое опр-е вероятности

1. Люба включает телевизор. Телевизор включается на случайном канале. В это время по четырем каналам из шестнадцати показывают музыкальные клипы. Найти вероятность того, что Люба попадет на канал, где клипы не идут.
2. Люба включает телевизор. Телевизор включается на случайном канале. В это время по шести каналам из сорока восьми показывают документальные фильмы. Найти вероятность того, что Люба попадет на канал, где документальные фильмы не идут.
3. В сборнике билетов по физике всего 40 билетов, в 6 из них встречается вопрос по теме «Термодинамика». Найти вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Термодинамика».
4. В сборнике билетов по биологии всего 25 билетов, в 9 из них встречается вопрос по теме «Круглые черви». Найти вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Круглые черви».

5. В чемпионате мира участвуют 15 команд. С помощью жребия их нужно разделить на пять групп по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в четвёртой группе?

Задачи на классическое опр-е вероятности (2)

6. В чемпионате мира участвуют 10 команд, среди которых есть команда Канады. С помощью жребия их нужно разделить на пять пар. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 2, 2, 3, 3, 4, 4, 5, 5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Канады окажется в первой группе?

7. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найти вероятность того, что он прослужит меньше двух лет, но больше года.
8. Вероятность того, что новый пылесос прослужит больше года, равна 0,95. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найти вероятность того, что он прослужит меньше двух лет, но больше года.
9. Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной?
10. В среднем из 2000 садовых насосов, поступивших в продажу, 6 подтекают. Найти вероятность того, что один случайно выбранный для контроля насос не подтекает?

Задачи на классическое опр-е вероятности (3)

11. В среднем из 1300 садовых насосов, поступивших в продажу, 13 подтекают. Найти вероятность того, что один случайно выбранный для контроля насос не подтекает.

12. Фабрика выпускает сумки. В среднем из 125 сумок, поступивших в продажу, 5 сумок имеют скрытый дефект. Найти вероятность того, что случайно выбранная сумка окажется без скрытых дефектов.
13. Фабрика выпускает сумки. В среднем на 50 качественных сумок приходится пять сумок со скрытыми дефектами. Найти вероятность того, что купленная сумка окажется качественной. Результат округлить до сотых.
14. Фабрика выпускает сумки. В среднем на 120 качественных сумок приходится восемь сумок со скрытыми дефектами. Найти вероятность того, что купленная сумка окажется качественной. Результат округлить до сотых.
15. Научная конференция проводится в 4 дня. Всего запланировано 60 докладов: первые два дня — по 12 докладов, остальные распределены поровну между третьим и четвёртым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

Задачи на классическое опр-е вероятности (4)

16. Научная конференция проводится в 4 дня. Всего запланировано 50 докладов: первые два дня — по 13 докладов, остальные доклады распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора К. Порядок докладов определяется случайным образом. Какова вероятность того, что доклад профессора К. окажется запланированным на последний день конференции?
17. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и больше 3?
18. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет меньше 4?
19. На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 8 прыгунов из России и 10 прыгунов из Мексики. Порядок выступлений определяется жеребьёвкой. Найти вероятность того, что пятнадцатым будет выступать прыгун из России.
20. На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 9 прыгунов из России и 12 прыгунов из Китая. Порядок выступлений определяется жеребьёвкой. Найти вероятность того, что третьим будет выступать прыгун из Китая.

Задачи на классическое опр-е вероятности (5)

21. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из России будет выступать после группы из Вьетнама и после группы из Англии? Результат округлить до сотых.
22. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Китая будет выступать после группы из Вьетнама и после группы из Канады? Результат округлить до сотых.
23. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найти вероятность того, что во второй раз выпало 3 очка.
24. Игральный кубик бросают дважды. Известно, что в сумме выпало 5 очков. Найти вероятность того, что в первый раз выпало 2 очка.
25. При двукратном бросании игральной кости в сумме выпало 9 очков. Какова вероятность того, что хотя бы раз выпало 5 очков?
26. При двукратном бросании игральной кости в сумме выпало 6 очков. Какова вероятность того, что хотя бы раз выпало 3 очка?

Задачи на классическое опр-е вероятности (6)

27. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найти вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 4 часа.
28. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найти вероятность того, что часовая стрелка застыла, достигнув отметки 8, но не дойдя до отметки 11 часов.
29. Найти вероятность того, что случайно выбранное трёхзначное число делится на 33.
30. Найти вероятность того, что случайно выбранное трёхзначное число делится на 25.
31. В ящике находятся чёрные и белые шары, причём чёрных в 3 раза больше, чем белых. Из ящика случайным образом достали один шар. Найти вероятность того, что он будет белым.

32. В ящике находятся чёрные и белые шары, причём чёрных в 9 раз больше, чем белых. Из ящика случайным образом достали один шар. Найти вероятность того, что он будет белым.

Задачи на классическое опр-е вероятности (7)

33. В случайном эксперименте бросают две игральные кости. Найти вероятность того, что сумма выпавших очков равна 6. Результат округлить до сотых.

34. В случайном эксперименте бросают две игральные кости. Найти вероятность того, что в сумме выпадет 10 очков. Результат округлить до сотых.

Алгебра событий

A

B

{A}\cdot \overline{B}

A

B

A

B

A

B

\Omega

B

A

B

\Omega

A

B

\Omega

A + B

AB

\Omega

\overline{B}

A

B

\Omega

\overline{A}

A

B

\Omega

{A}\cdot \overline{B}

\Omega

{A}\cdot \overline{B}

A

B

A

B

\overline{A}\cdot B

\Omega

или

и

все, кроме

только

A

B

A

B

A

B

A

B

Сумма событий (совместных)

Операция сложения событий означает логическую связку ИЛИ.

Суммой двух событий и называется событие, которое состоит в том, что наступит или событие , или событие , или оба события одновременно, если события совместны.

A

B

A

B

A =

B =

A + B

'трефа'

'туз'

Пример:

P(A + B) = P(A) + P(B) - P(A) \cdot P(B)

A

B

\Omega

Сумма событий (несовместных)

Операция сложения событий означает логическую связку ИЛИ.

A

B

В том случае, если события несовместны, наступление обоих событий — отпадает, то есть может наступить или событие или событие .

Пример:

A =

B =

'удовл. за экзамен'

'хор. за экзамен'

A + B

A

B

A

\Omega

P(A + B) = P(A) + P(B)

Произведение событий (независимых)

Операция произведения событий означает логическую связку И.

Произведением двух независимых событий и называют событие , которое состоит в совместном появлении этих событий, иными словами, умножение означает, что при некоторых обстоятельствах наступит и событие , и событие .

A

B

A

B

Пример:

A_1 =

B_1 =

'на первой монете орел'

'на второй монете орел'

\Rightarrow

A_2 =

B_2 =

'на первой монете решка'

'на второй монете решка'

A_1B_2

A_2B_2

P(AB) = P(A) \cdot P(B)

B

A

\Omega

Произведение событий (зависимых)

Операция произведения событий означает логическую связку И.

Вероятность события , вычисленная при условии, что имеет место событие , называется условной вероятностью события при условии появления и обозначается или . .

Вероятность появления произведения двух событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло:

A

B

A

B

P(A B) = P(A) \cdot P_A(B) = P(B) \cdot P_B(A)

P_B(A)

P(A/B)

Пример: Ученик дважды извлекает по одному билету из 34. Какова вероятность того, что он сдаст экзамен, если им подготовлено 30 билетов и в первый раз вынут неудачный билет?

P(AB) = P(A) \cdot P_A(B) = \frac{4}{34} \cdot \frac{30}{33} = \frac{20}{187}.

Решение:

Вероятность того, что первый билет неудачный

Вероятность того, что первый билет удачный, но с учетом того, что один билет уже вытянут

Примеры задач на теоремы вероятностей

Задачи на деревья

1. Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 5% яиц из первого хозяйства  — яйца высшей категории, а из второго хозяйства  — 30% яиц высшей категории. В этой агрофирме 15% яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение: Построим дерево событий:

I хоз-во

II хоз-во

высш кат.

др. кат.

0{,}05

0{,}3

x

1-x

1-0{,}05

1-0{,}3

0{,}15 \Sigma

\Rightarrow x \cdot 0{,}05 + (1-x) \cdot 0{,}3 = 0{,}15

0{,}05 x + 0{,}3 - 0{,}3x = 0{,}15

x = 0{,}6

* где — вероятность того, что яйцо I хоз-ва

x

Задачи на рассадку

2.

Задачи про автоматы

3. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

A =

'исправен первый автомат';

B =

'исправен второй автомат';

P(A) = 1 - 0{,}05 = 0{,}95

P(B) = 1 - 0{,}05 = 0{,}95

события совместные

A

B

\Omega

т.н.:

P(A+B).

P(A+B) = P(A) + P(B) - P(A)\cdot P(B) = 0{,}95 + 0{,}95 - 0{,}95 \cdot0{,}95 = 0,9975.

Решение:

\Rightarrow

Задачи про шахматистов

3. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

A =

'выиграет белыми';

B =

'выиграет черными';

P(A) = 0{,}52

P(B) = 0{,}3

события независимые

т.н.:

P(A \cdot B) = P(A) \cdot P(B) = 0{,}52 \cdot 0{,}3  =  0{,}156.

Решение:

P(A \cdot B).

Теория вероятностей

Что такое теория вероятностей?

События

Пространство исходов. Группы событий

Взаимосвязь событий

Равновероятные события

Совместные и несовместные события

Противоположные события

Зависимые и независимые события

Классическое определение вероятности

Примеры задач на классическое определение вероятности

Элементарные задачи

Задачи на жребьевку

Задачи с числовыми осями

Задачи «в среднем»

Задачи на классическое опр-е вероятности

Задачи на классическое опр-е вероятности (2)

Задачи на классическое опр-е вероятности (3)

Задачи на классическое опр-е вероятности (4)

Задачи на классическое опр-е вероятности (5)

Задачи на классическое опр-е вероятности (6)

Задачи на классическое опр-е вероятности (7)

Алгебра событий

Алгебра событий

Сумма событий (совместных)

Сумма событий (несовместных)

Произведение событий (независимых)

Произведение событий (зависимых)

Примеры задач на теоремы вероятностей

Задачи на деревья

Задачи на рассадку

Задачи про автоматы

Задачи про шахматистов

А0. Теория вероятностей

А0. Теория вероятностей

vkrysanov320

Теория вероятностей

Что такое теория вероятностей?

События

Пространство исходов. Группы событий

Взаимосвязь событий

Равновероятные события

Совместные и несовместные события

Противоположные события

Зависимые и независимые события

Классическое определение вероятности

Примеры задач на классическое определение вероятности

Элементарные задачи

Задачи на жребьевку

Задачи с числовыми осями

Задачи «в среднем»

Задачи на классическое опр-е вероятности

Задачи на классическое опр-е вероятности (2)

Задачи на классическое опр-е вероятности (3)

Задачи на классическое опр-е вероятности (4)

Задачи на классическое опр-е вероятности (5)

Задачи на классическое опр-е вероятности (6)

Задачи на классическое опр-е вероятности (7)

Алгебра событий

Алгебра событий

Сумма событий (совместных)

Сумма событий (несовместных)

Произведение событий (независимых)

Произведение событий (зависимых)

Примеры задач на теоремы вероятностей

Задачи на деревья

Задачи на рассадку

Задачи про автоматы

Задачи про шахматистов

А0. Теория вероятностей

More from vkrysanov320