Перпендикулярность прямой и плоскости
10 класс
vkrysanov320@gmail.com
version 1.1, 30-11-2022
Перпендикулярные прямые в пространстве
Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен .
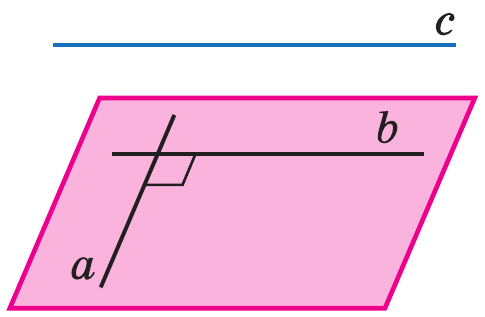
Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
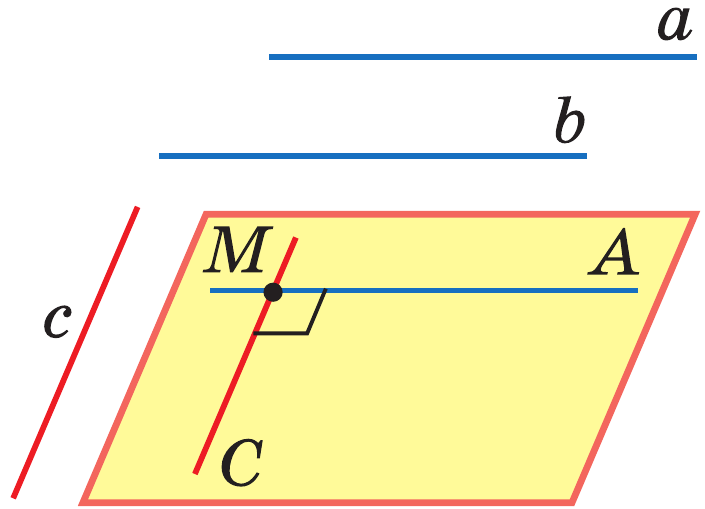
Пусть
Т. д.
Параллельные прямые, перпендикулярные к плоскости
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
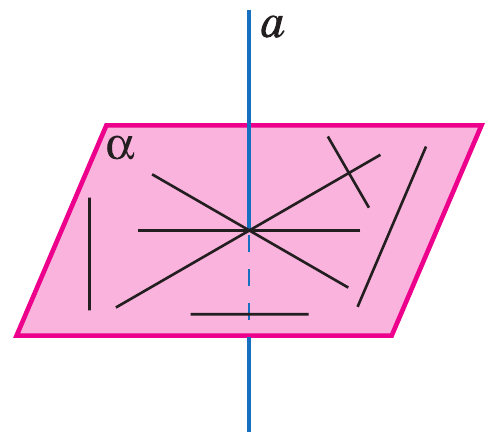
Теорема: Eсли две прямые перпендикулярны к плоскости, то они параллельны.
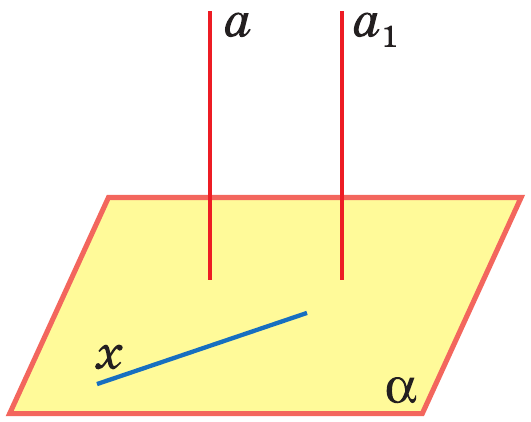
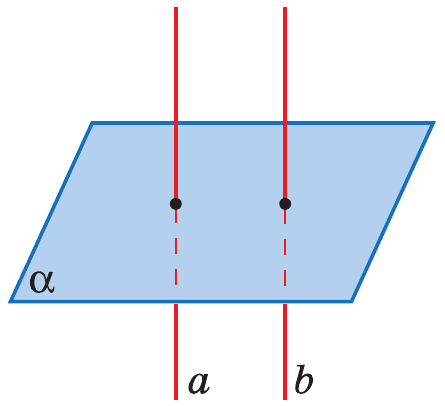
Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Признак перпендикулярности прямой и плоскости
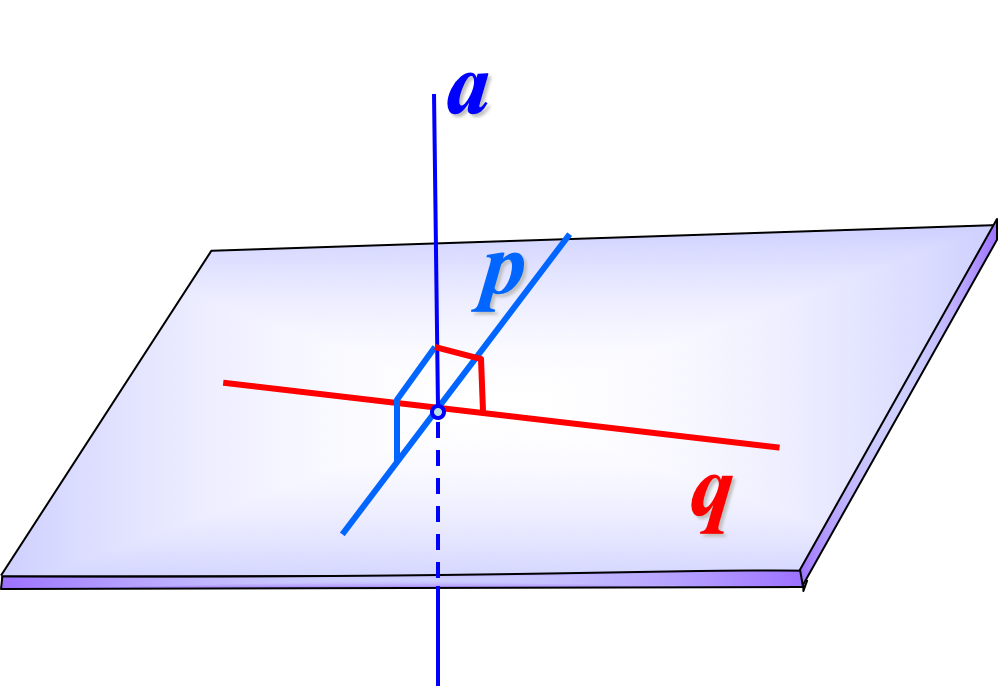
Eсли прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
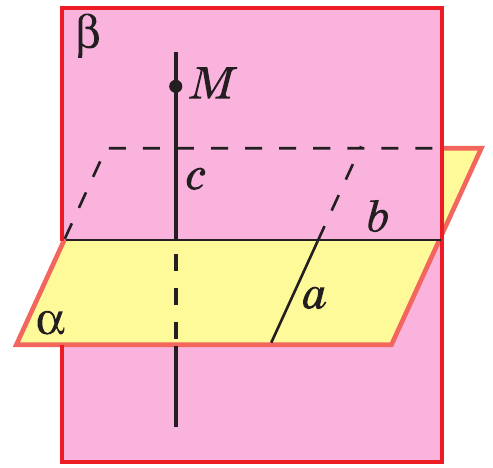
Теорема о прямой, перпендикулярной к плоскости
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Задачи
т. д.
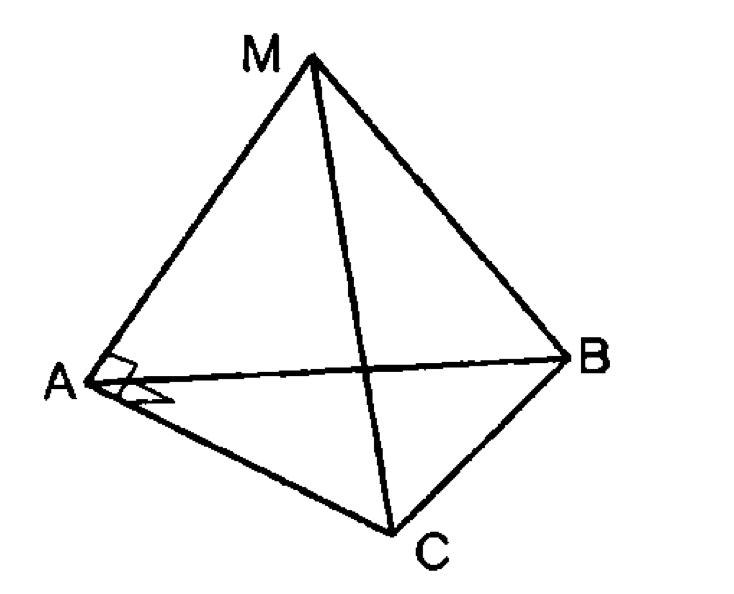
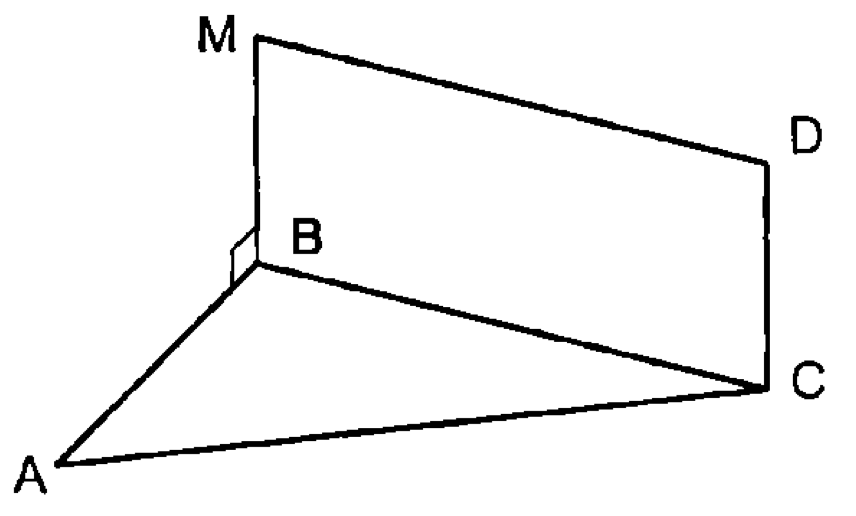
т. д.
— прямоугольник
1.
2.
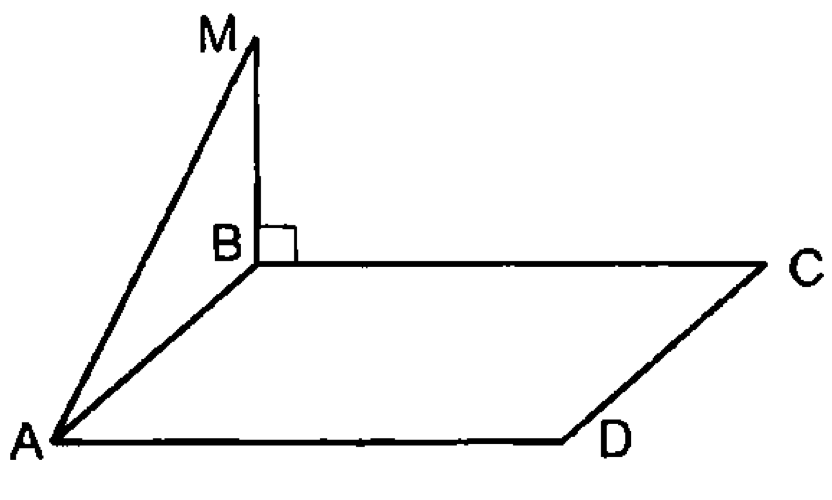
т. д.
— прямоугольник
4.
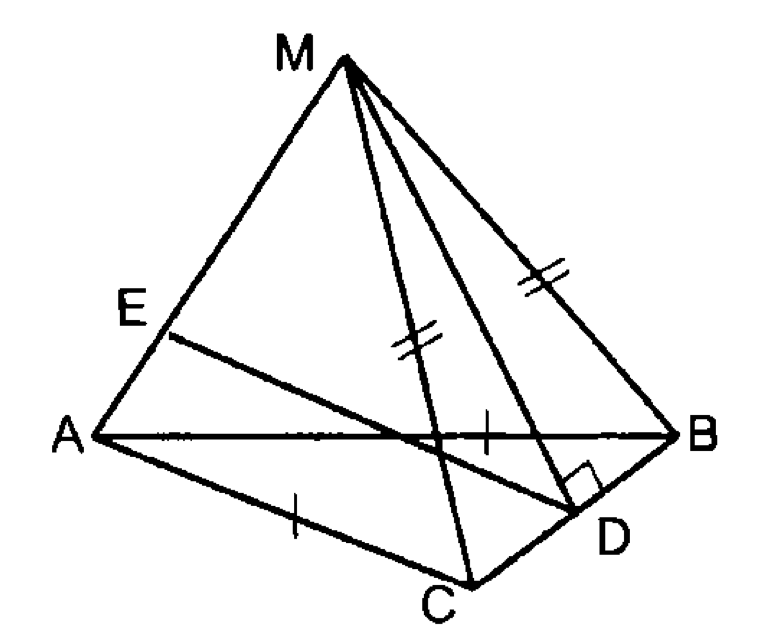
3.
т. д.
Задачи (2)
т. д.
5.
— параллелограмм
6.
т. д.
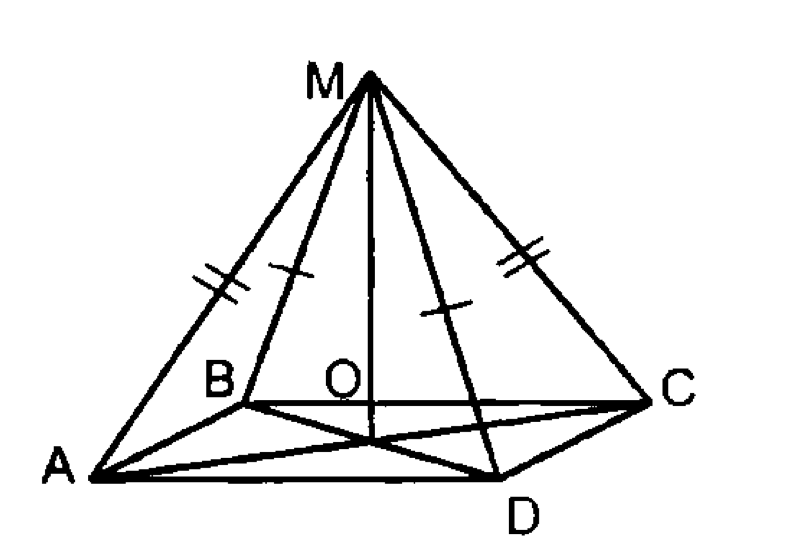
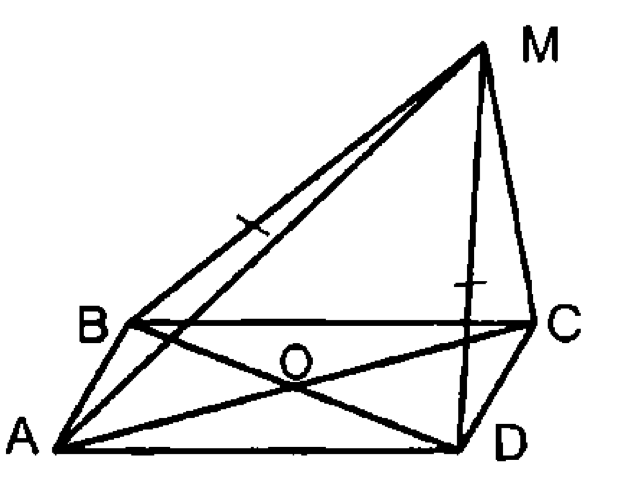
— ромб
Задачи (3)
т. н.
7.
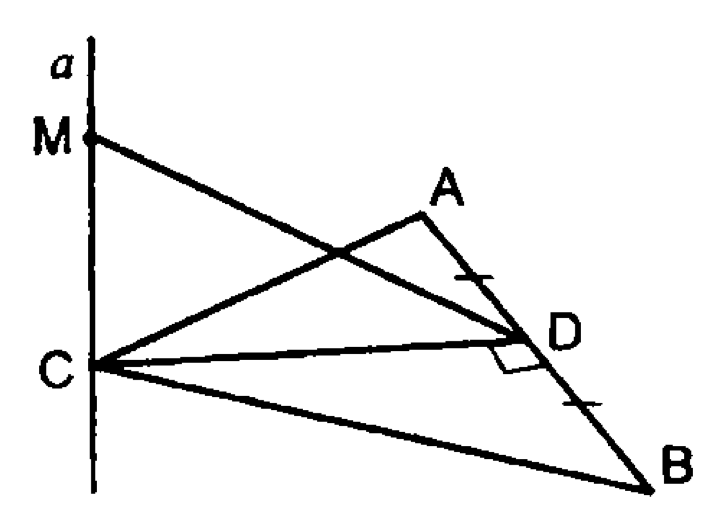
8.
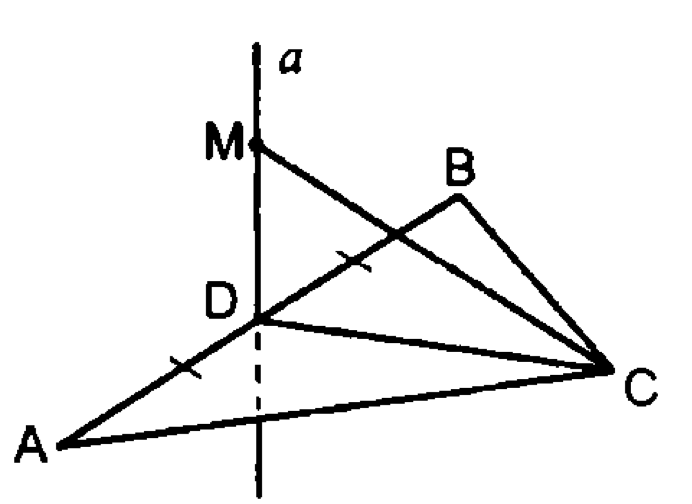
— равносторонний
т. н.
Задачи (4)
т. н.
9.
10.
т. н.
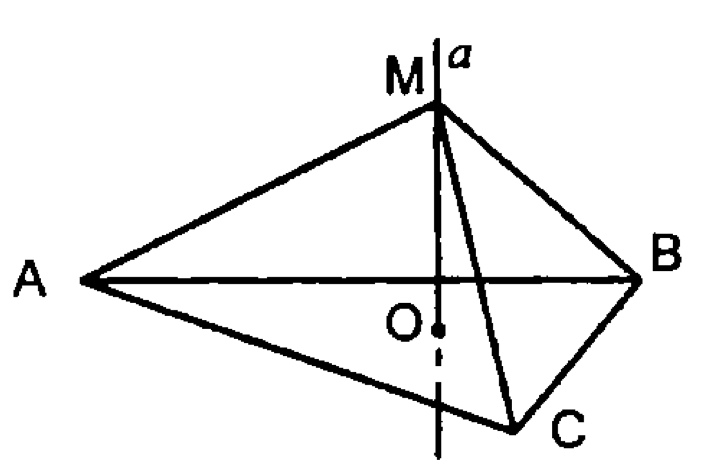
— равносторонний
— центр описанной окружности у
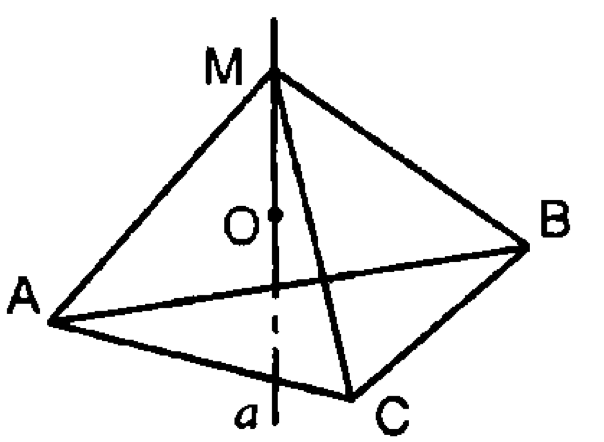
— центр описанной окружности у
Задачи (5)
т. н.
11.
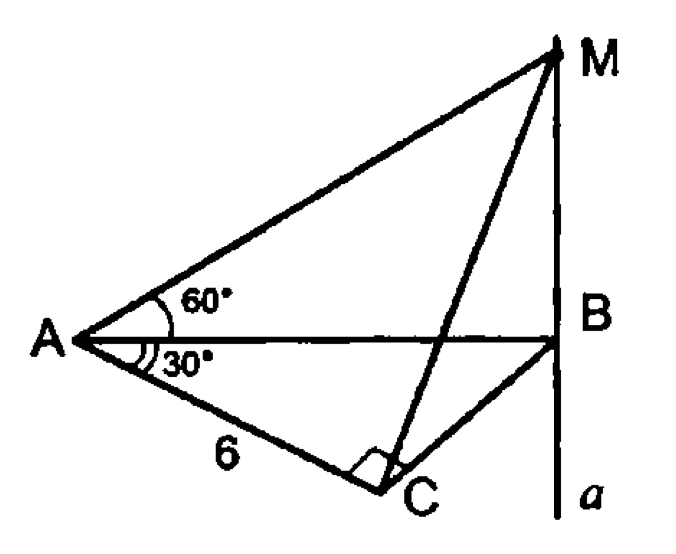
12.
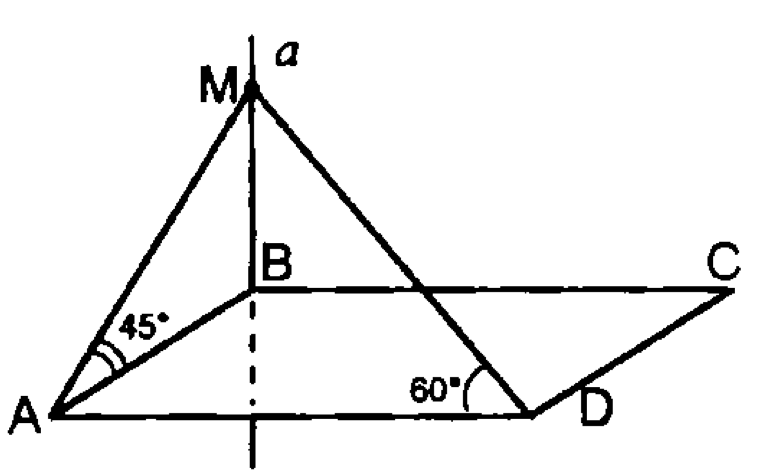
— прямоугольник
т. н.
Задачи (6)
13. Прямая перпендикулярна к плоскости правильного треугольника . Через центр этого треугольника проведена прямая , параллельная прямой Известно, что . Найти расстояния от точек и до вершин и треугольника.
14. Через точки и прямой проведены прямые, перпендикулярные к плоскости и пересекающие ее соответственно в точках и . Найдите , если
Г3. Перпендикулярность прямой и плоскости
By vkrysanov320
Г3. Перпендикулярность прямой и плоскости
- 1,001



