Algorithms #10
Heaps

Lets start from the interview question
We have a list of points on the plane. Find the K closest points to the origin (0, 0).
(1; 1)
(3; 2)
(-0.3; -0.4)
(-2; -1)
Data = [[3, 2], [1,1], [-0.3, -0.4], [-2, -1]], k = 2
x
y
Res = [ [-0.3, -0.4], [1,1]], k = 2

Another question
Kth Largest Element in an Array
Given [3,2,1,5,6,4] and k = 2, return 5.
One of the possible solutions is using a Heap
Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly.
What is a Heap ?
The maximum number of children of a node in a heap depends on the type of heap. However, in the more commonly-used heap type, there are at most 2 children of a node and it's known as a Binary heap
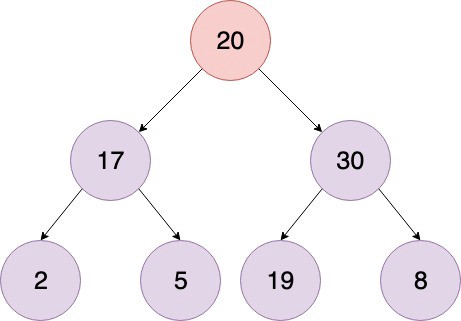
Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.

Other types of heaps
When would I want to use a heap?
- Whenever you need quick access to the largest (or smallest) item
- Queues / Schedulers (where the earliest item is desired)
- Heapsort: One of the best sorting methods being in-place and with no quadratic worst-case scenarios.
- Selection algorithms: Finding the min, max, both the min and max, median, or even the k-th largest element
- Graph algorithms: By using heaps as internal traversal data structures, run time will be reduced by polynomial order.

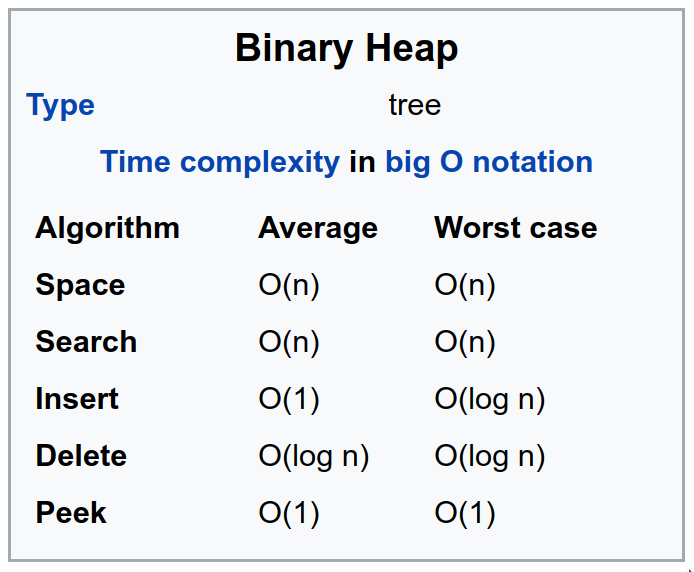
The complexity
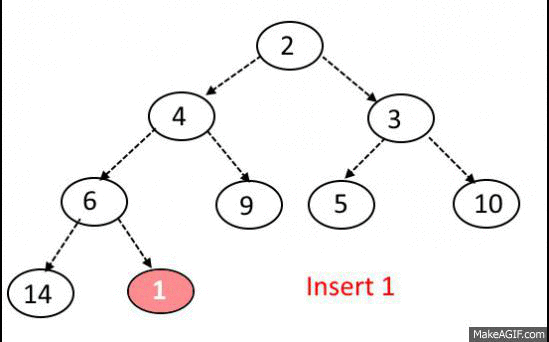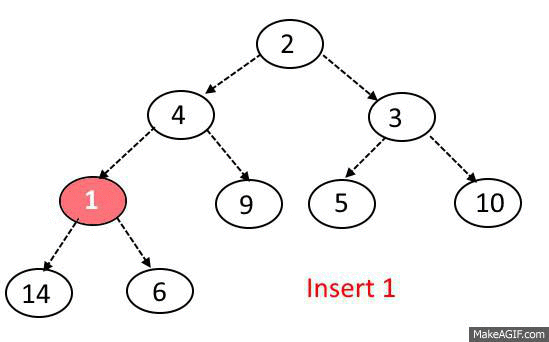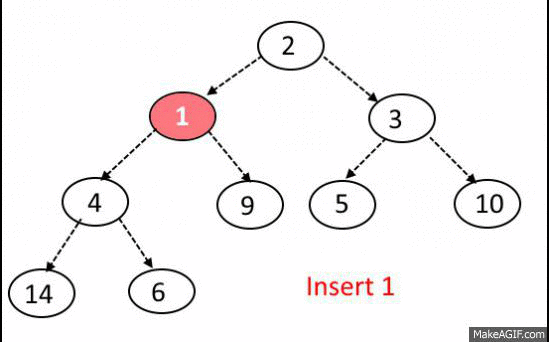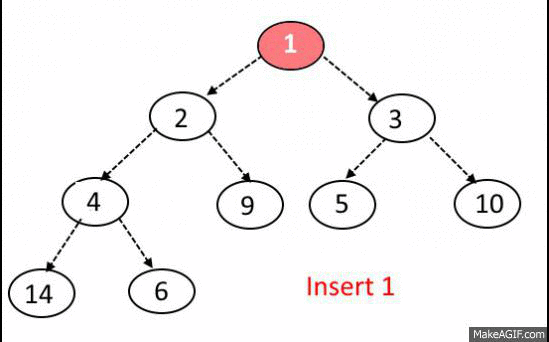
A heap can be implemented using objects links (like we did for BST) and the Array!
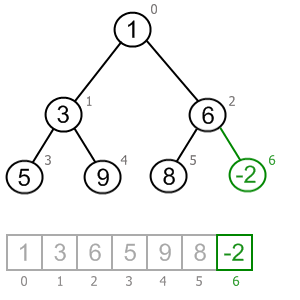
<-- Figure out this!
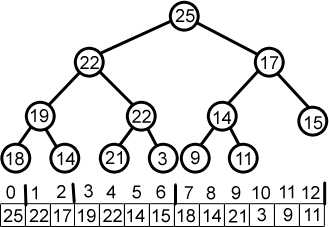
Parent = (index-1)/2
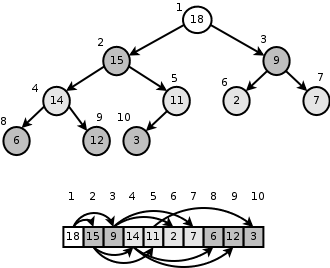
Left child index*2 + 1
Right child index*2 + 2
Push algorithm
- Place new element to the end of array
- Find parent index
- Check if parent element is on his place
- Move recursively on top node or stop the execution.
class Heap {
constructor() {
this.data = [];
this.size = 0;
}
bubbleUp() { /* ... */ }
put(val) { /* ... */ }
print() { console.log(this.data) }
}
const heap = new Heap();
heap.push(20);
heap.push(10);
heap.push(30);
heap.push(1);
heap.push(100);
heap.print(); // [ 100, 30, 20, 1, 10 ]Problem #1
Implement .push(val) method
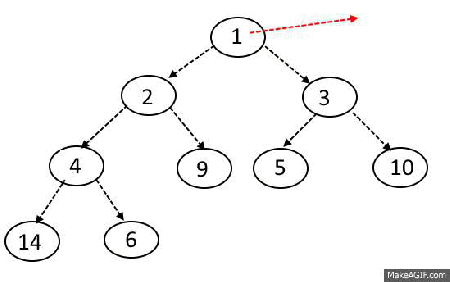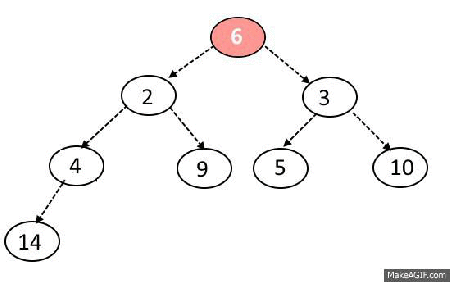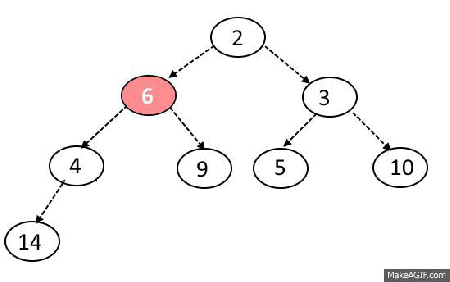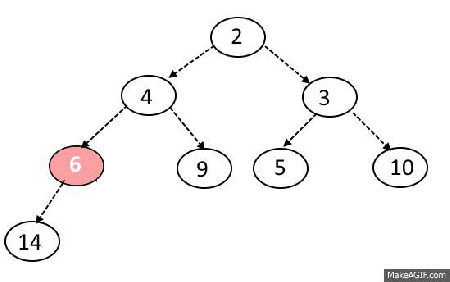
Pop algorithm
- Remove first item in array (and return it later)
- Place last item of array to the first place
- Check if left or right child is bigger than current node
- Move down recursively until you all childs will be smaller than current node
}
Max-Heapify
Problem #2
Implement .pop() method
class Heap {
constructor() {
this.data = [];
this.size = 0;
}
bubbleUp() { /* ... */ }
put(val) { /* ... */ }
print() { console.log(this.data) }
maxHeapify() { /* ... */ }
pop() { /* ... */ }
}
Problem #3
Implement .buildMaxHeap(arr) method
class Heap {
/* ... */
buildMaxHeap(arr = []) { /* ... */ }
}
const heap = new Heap();
heap.buildMaxHeap([1,20,10,100,30]);
heap.print(); // [ 100, 30, 20, 1, 10 ]Priority Queue
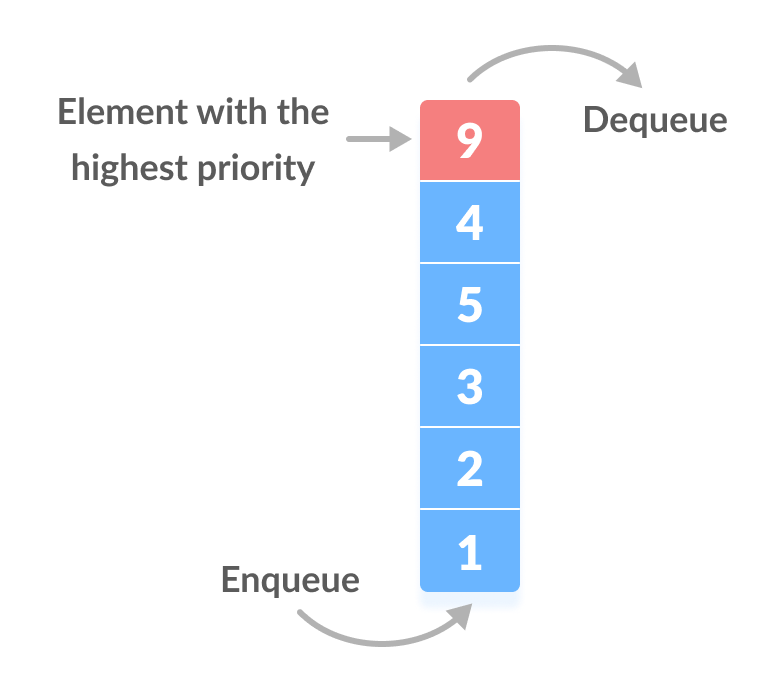
Applications of Priority Queue
- Dijkstra's shortest path algorithm implementation can be done using priority queues.
- A* Search algorithm implementation can be done using priority queues.
- Priority queues are used to sort heaps.
- Priority queues are used in operating system for load balancing and interrupt handling.
- Priority queues are used in huffman codes for data compression.
- In traffic light, depending upon the traffic, the colors will be given priority.
Problem #4
Refactor a Heap class, so you can use it as a priority queue

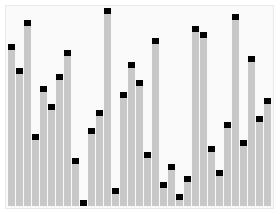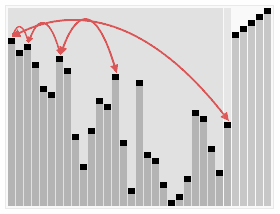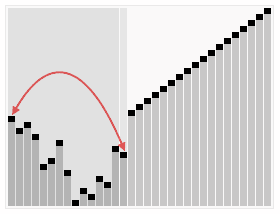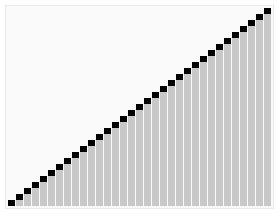
HeapSort
Heap sort is a comparison based sorting technique based on Binary Heap data structure. It is similar to selection sort where we first find the maximum element and place the maximum element at the end. We repeat the same process for remaining element.
Time Complexity: Time complexity of heapify is O(Log n). Overall time complexity of Heap Sort is O(n Log n).
Problem #5
Use Heap to sort an array

Thank you!

Algorithms #10
By Vladimir Vyshko
Algorithms #10
Heap, Binary tree, Priority Queue
- 714



