Algorithms #11
Graphs

How would you implement a map ?
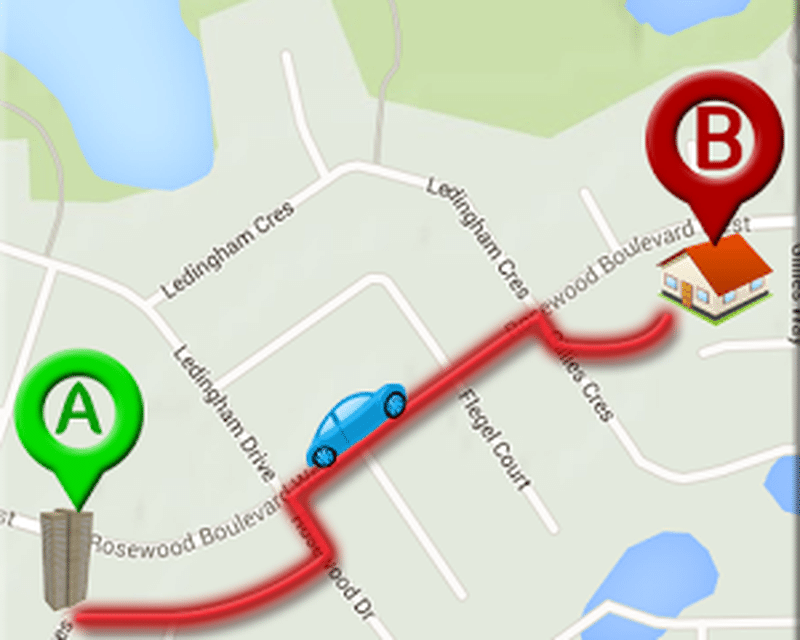
Lets make an abstraction: a set of nodes connected with edges
This is a graph !
A Graph is a non-linear data structure consisting of nodes and edges.
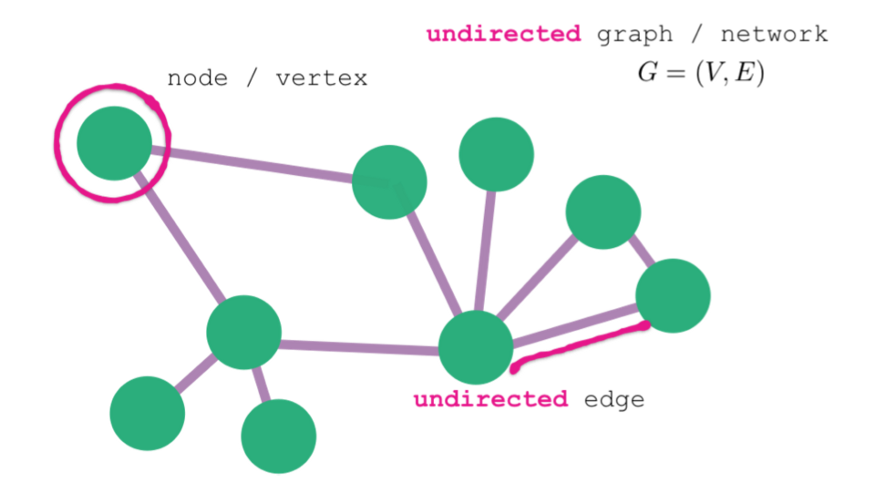
A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes.
Use cases of graphs
1. Maps
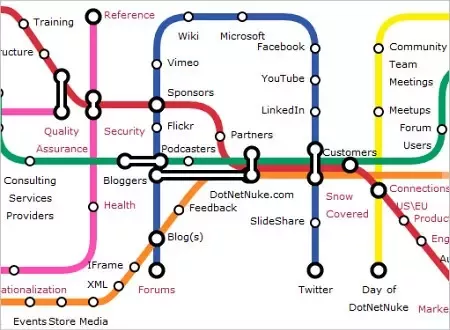
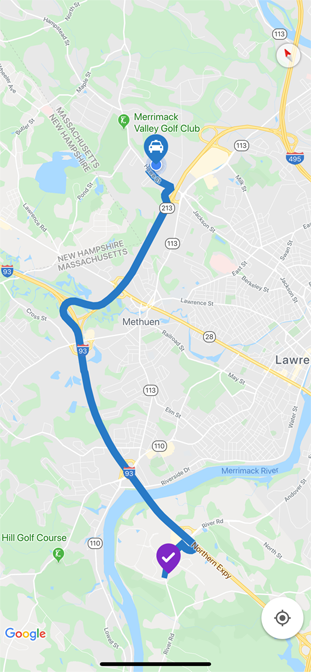
The best way of drawing subway maps can be easily solved using graph theory.
2. Chemical models
Most widely used chemical models are graph models
3. Facebook friends connection
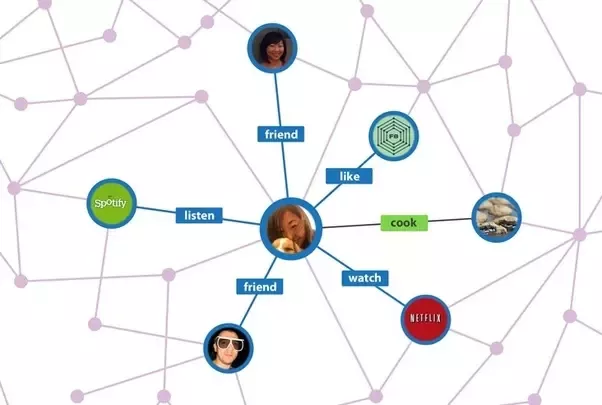
Facebook (and almost all other social networks) model the users and their connections with their friends in a graph structure. And, they use this graph model to do their business by applying graph theory ideas, including how to populate your timeline, what advertisements to show, etc.
4. Your favorite search engine
Google, uses a graph representation to store/retreive the semantic relationship between different entities, which they call it, Knowledge Graph, as well as providing you with the top relevant webpages for your query, using PageRank algorithm, which is a graph theorethic algorithm.

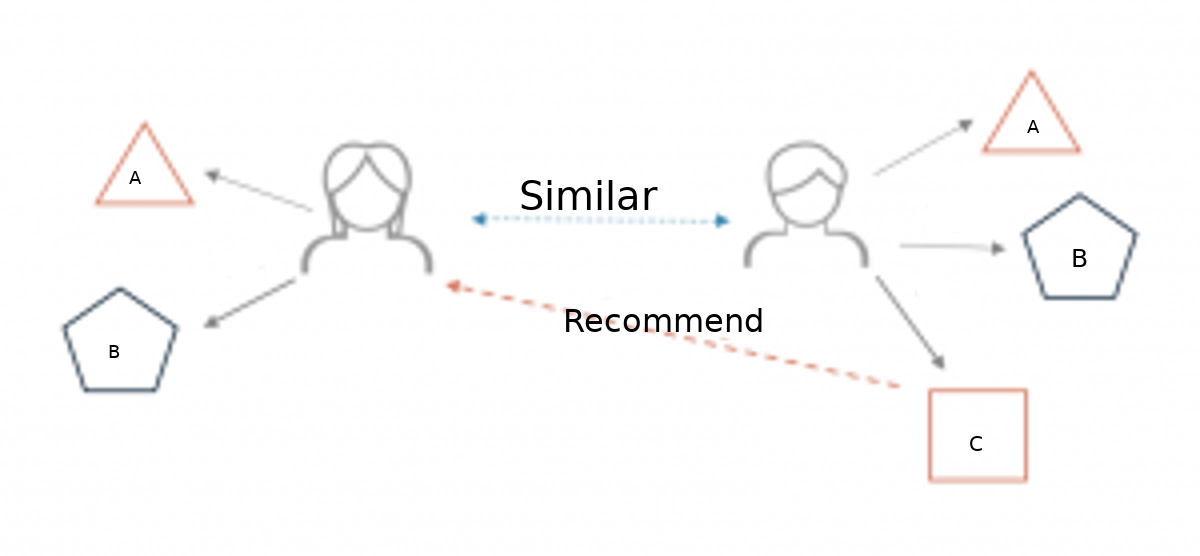
5. Almost every recommendation system
including the ones used by Amazon for recommending you the relevant books to buy, or Netflix for recommending you what to watch use graph theoretic algorithms.
6. Networking
Your entire Internet works on the principle of Graph Theory.
Also
- Graph theory is used in biology and conservation efforts where a vertex represents regions where certain species exist and the edges represent migration path or movement between the regions.
- Graph theoretical concepts are widely used in Operations Research.
- Dependecy management / representation
- File system
- The networks may include paths in a telephone network.
- Graphs are used to solve many real-life problems.

Graphs are important!

Terminology
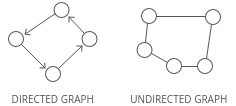
Directed or undirected
In directed graphs, edges point from the node at one end to the node at the other end. In undirected graphs, the edges simply connect the nodes at each end.
Cyclic or acyclic
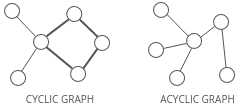
graph is cyclic if it has a cycle—an unbroken series of nodes with no repeating nodes or edges that connects back to itself. Graphs without cycles are acyclic.
Weighted or unweighted
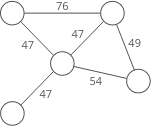
If a graph is weighted, each edge has a "weight." The weight could, for example, represent the distance between two locations, or the cost or time it takes to travel between the locations.
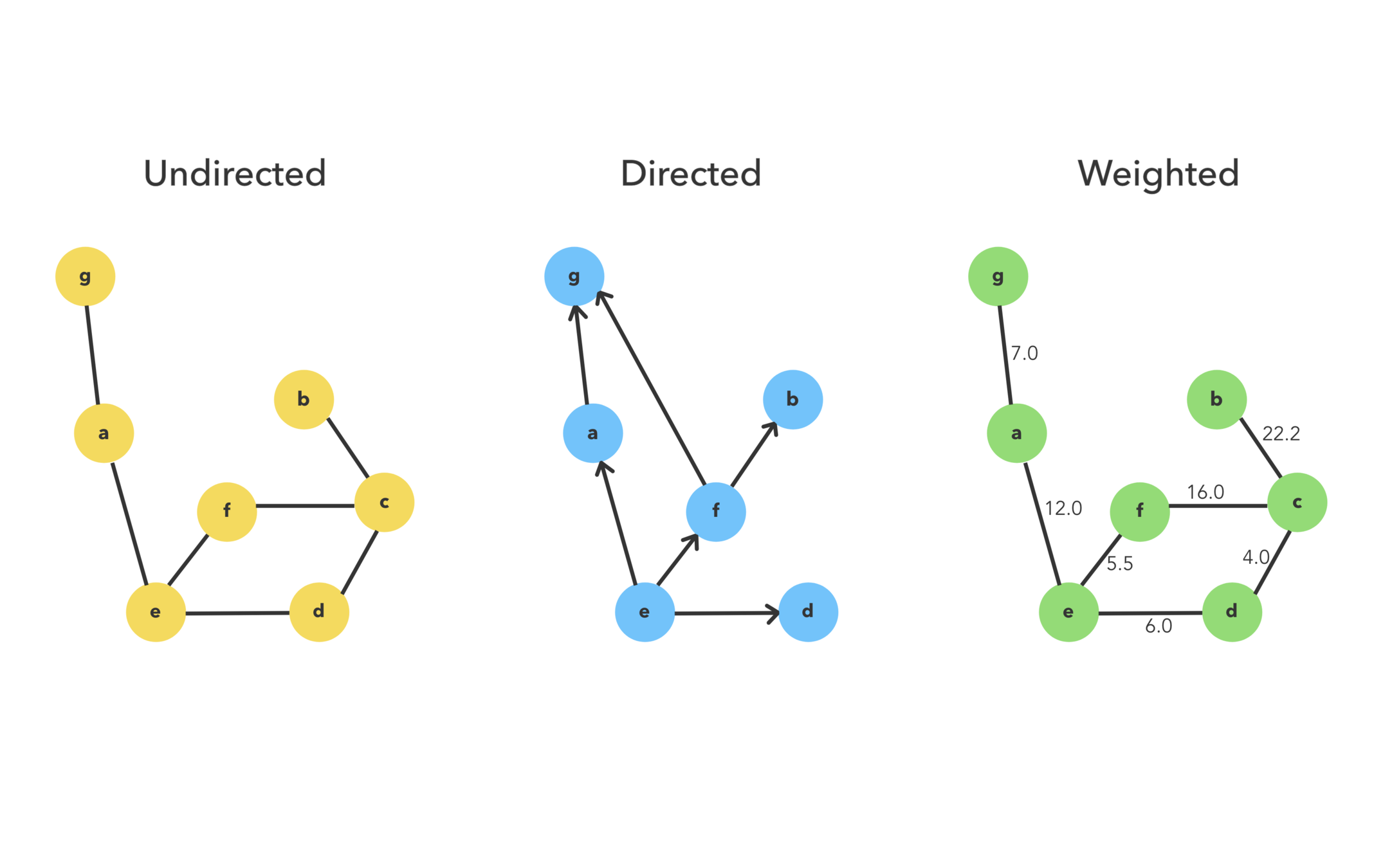
Types of graphs
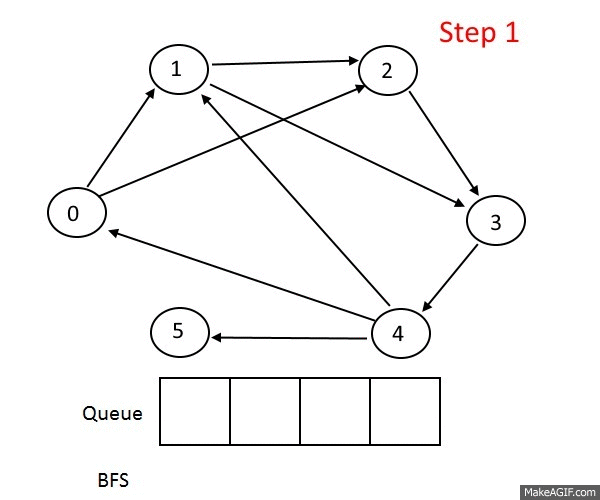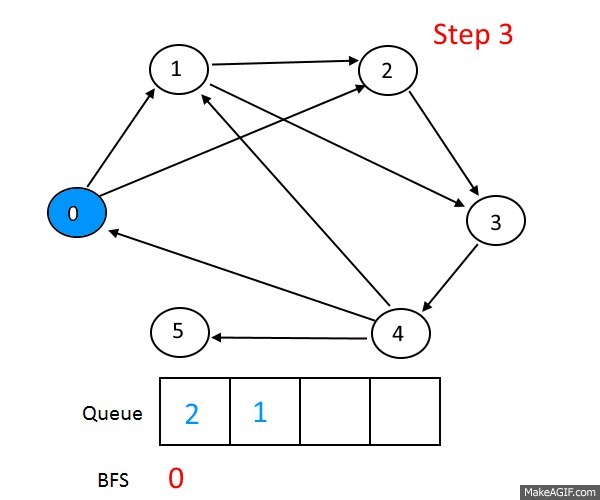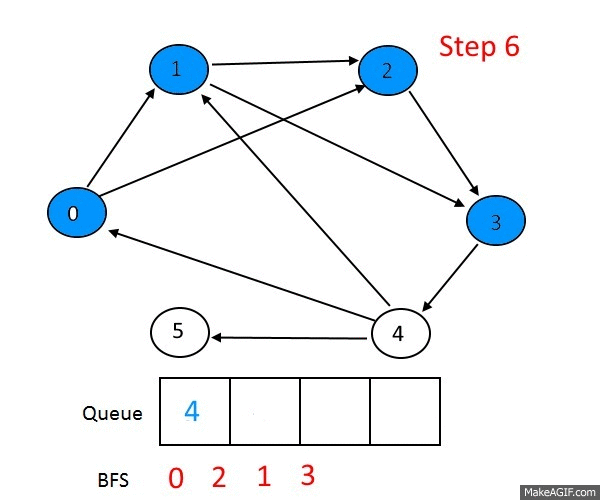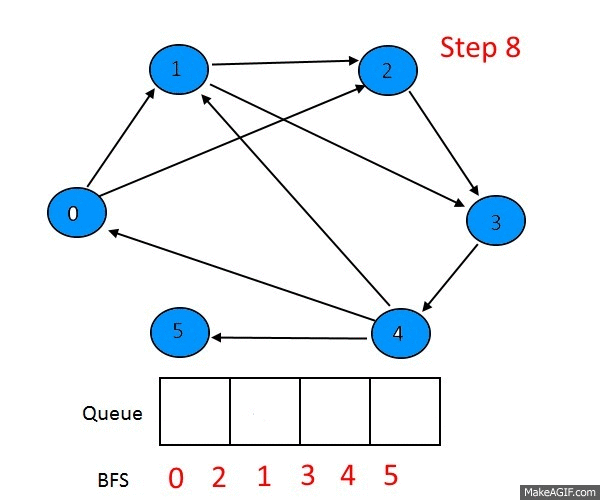
BFS and DFS
Lots of graph problems can be solved using just these traversals:
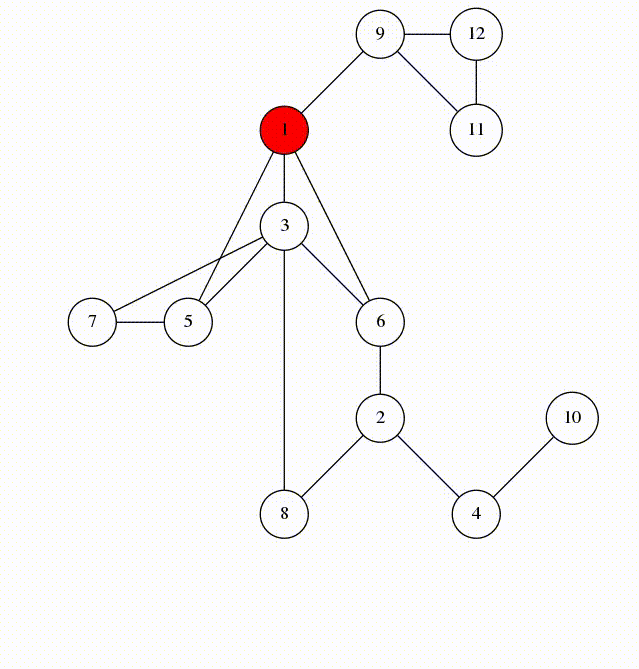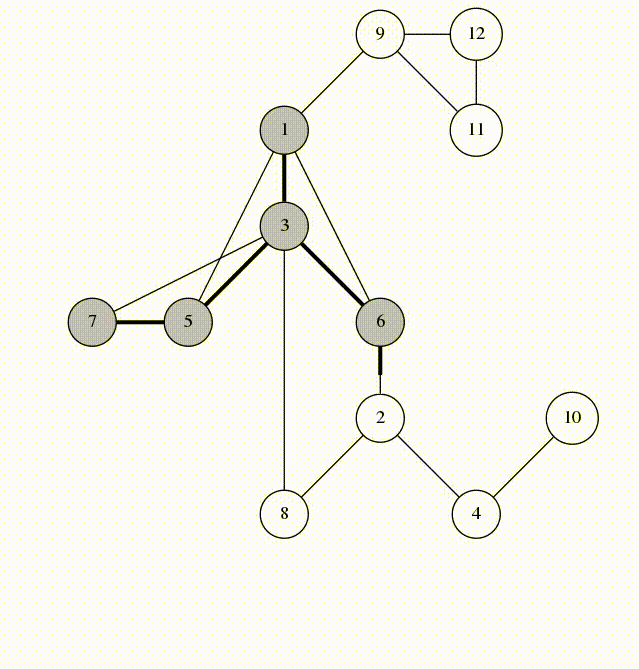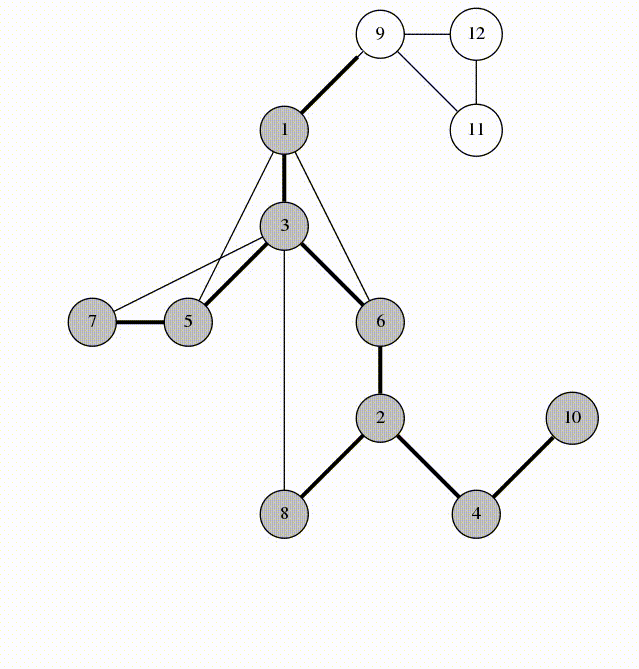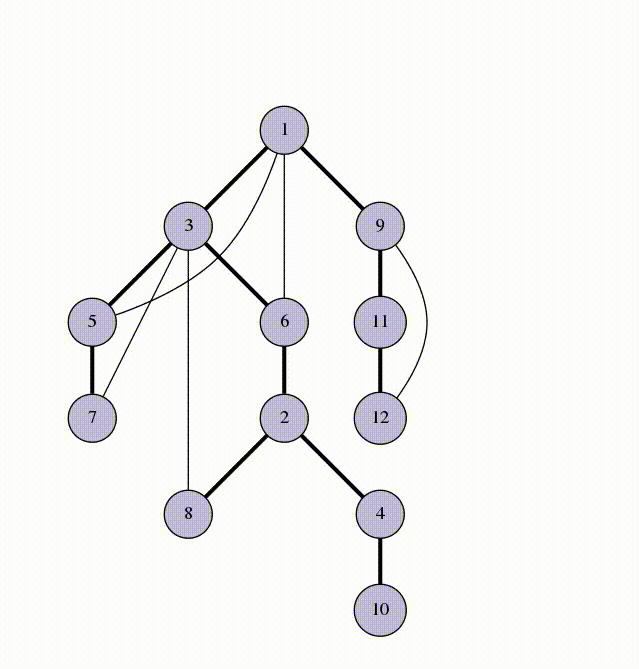
Advanced graph algorithms
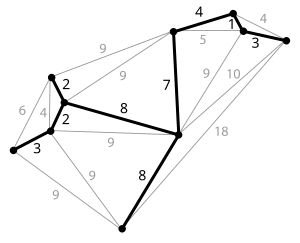
- Dijkstra's Algorithm: Finds the shortest path from one node to all other nodes in a weighted graph.
- Topological Sort: Arranges the nodes in a directed, acyclic graph in a special order based on incoming edges.
- Minimum Spanning Tree: Finds the cheapest set of edges needed to reach all nodes in a weighted graph.
Is there a path between two nodes in this undirected graph?
Run DFS or BFS from one node and see if you reach the other one.
What's the shortest path between two nodes in this undirected, unweighted graph?
Run BFS from one node and backtrack once you reach the second. Note: BFS always finds the shortest path, assuming the graph is undirected and unweighted. DFS does not always find the shortest path.
Does this undirected graph have a cycle?
Run BFS, keeping track of the number of times we're visiting each node. If we ever visit a node twice, then we have a cycle.
How to represent a graph in code ?
2 main approaches
Adjacency list
Adjacency matrix
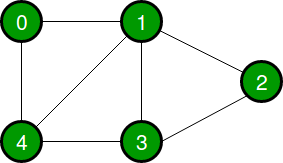
Adjacency Matrix

Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j

Adjacency List
An array of lists is used. Size of the array is equal to the number of vertices. Let the array be array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. Following is adjacency list representation of the above graph.
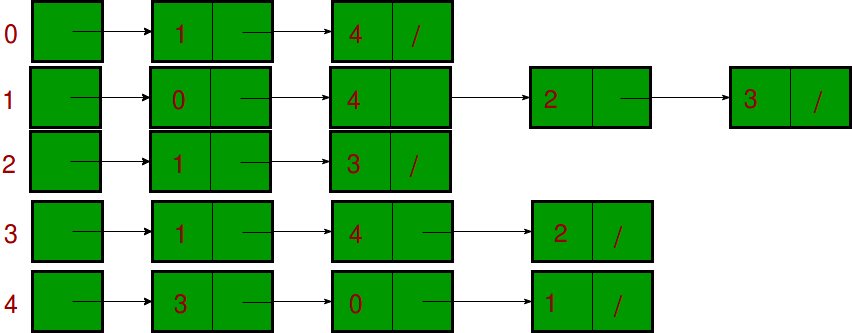
Which is better
Adjacency Matrix
- Uses O(n^2) memory
- It is fast to lookup and check for presence or absence of a specific edge
- between any two nodes O(1)
- It is slow to iterate over all edges
- It is slow to add/delete a node; a complex operation O(n^2)
- It is fast to add a new edge O(1)
Adjacency List
- Memory usage depends on the number of edges (not number of nodes),
- which might save a lot of memory if the adjacency matrix is sparse
- Finding the presence or absence of specific edge between any two nodes
- is slightly slower than with the matrix O(k); where k is the number of neighbors nodes
- It is fast to iterate over all edges because you can access any node neighbors directly
- It is fast to add/delete a node; easier than the matrix representation
- It fast to add a new edge O(1)
Lets try to implement our own Graph (Adjacency list)
class Graph {
constructor() {
// implement this
}
addVertex(name) {
// implement this
}
addEdge(v1, v2) {
// implement this
}
removeEdge(v1, v2) {
// implement this
}
removeVertex(v) {
// implement this
}
DFS(from = '') {
// implement this
}
hasPath(from, to) {
// implement this
}
}
const g = new Graph();
g
.addVertex('A')
.addVertex('B')
.addVertex('C')
.addVertex('D')
.addVertex('F')
.addEdge('A', 'B')
.addEdge('A', 'C')
.addEdge('B', 'C')
.addEdge('C', 'D')
.addEdge('D', 'A')
.addEdge('D', 'F');
// g.removeVertex('C');
// console.log(g.DFS('A'));
// console.log(g.hasPath('A', 'C'));
// console.log(g.hasPath('A', 'F'));
Thank you!

But first
let us recap previous topics
The complexity
What complexity is worse here:
1
1. O(2^n)
2. O(n^2)
What complexity is worse here:
2
1. O(2^n)
2. O(n!)
log(n) vs n ?
3
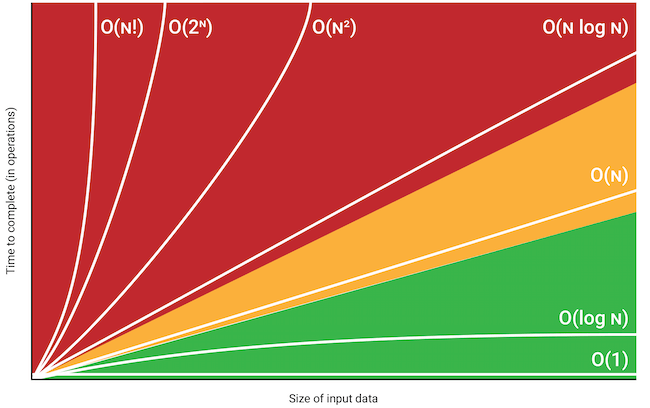
O(10n^2 + 1000) = ?
4
Simplify this:
O(n^2 + n!) = ?
5
Simplify this:
O(n*(10 + n*log(n))) = ?
6
Simplify this:
7
Represents the fastest possible running time:
Big Ω , Big θ, Big O ?
9
Represents the worst possible running time:
Big Ω , Big θ, Big O ?
10
Find the time complexity
function log(n) {
for (var i = 1; i <= Math.min(n, 100); i++) {
console.log(i);
}
}
11
Find the space complexity
function evenElementsArray(array) {
const newArray = Array(Math.ceil(array.length / 2));
for (var i = 0; i < array.length; i++) {
if (i % 2 === 0) {
newArray[i / 2] = array[i];
}
for (var j = 0; j < i; j++) { console.log(“hello”); }
}
return newArray;
}
12
Given an array of integers of size ‘n’. Our aim is to calculate the maximum sum of ‘k’ consecutive elements in the array.
Input : arr = [100, 200, 300, 400]
k = 2
Output : 700Window Sliding
13
Binary search time complexity
1. O(n)
2. O(n log(n))
3. O(log(n))
14
More uneversal algorithm
1. Linear search
2. Binary search
15
More fast algorithm
1. Linear search
2. Binary search
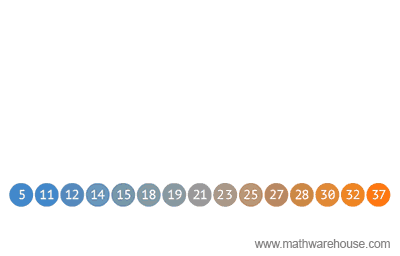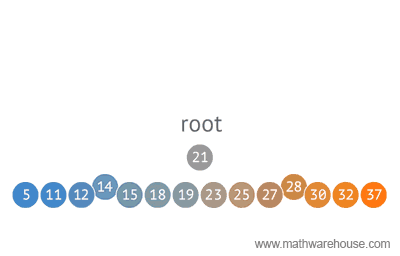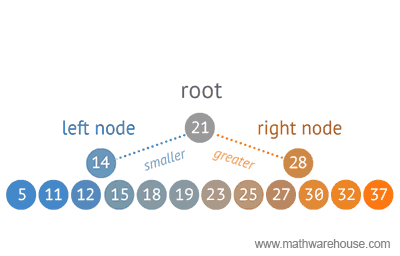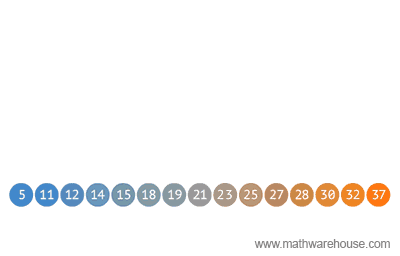
16
Big O (worst case) of quick sort
1. O(n^2)
2. O(n log(n))
17
Big O (worst case) of bubble sort
1. O(n^2)
2. O(n log(n))
18
QuickSort or Bubble sort ?
19
Stable sorting ?
20
Ok google what is it:


20
Ok google what is it:


21
Can we sort faster then O(n log n) ?
Recap
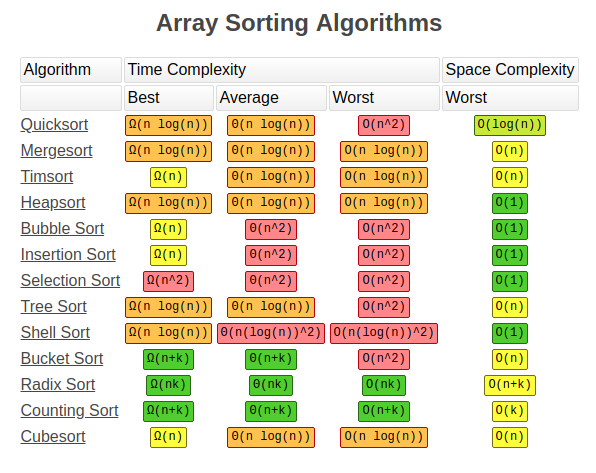
22
Linked list .push(data) complexity
1. O(n)
2. O(1)
3. O(log(n))
23
Is this a good idea to use binary search on a linked list ?
24
How to check that linked list has a loop ?
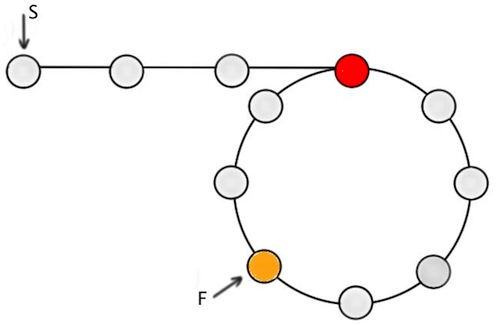

25
LIFO

1. Stack
2. Queue
26
Examples of using stacks ?

27
Stack vs Queue ?
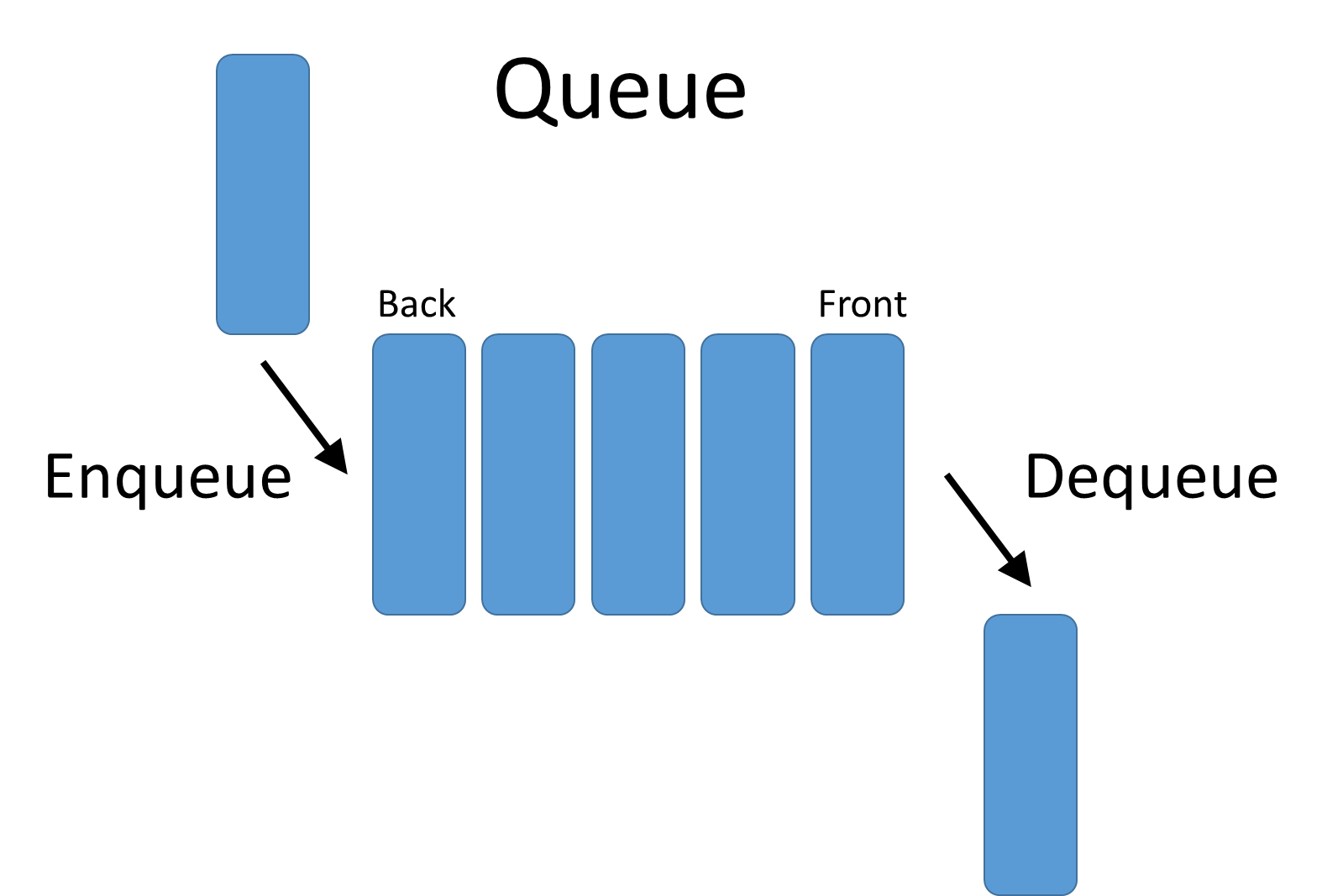
28
What is a map ?


29
Time complexity of .put(data)


1. O(n)
2. O(1)
30
new Map() vs {} ???


31
BST - what is it ?
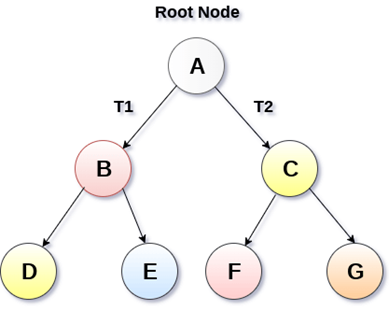
32
How to iterate over a tree ?

33
Recursive or iterative traversing ?


OK we are good
Algorithms #11
By Vladimir Vyshko
Algorithms #11
BFT, DFT, Graphs overview
- 873



