Weighted graphs

Algorithms #12
Lets solve few simple problems first
Problem #1
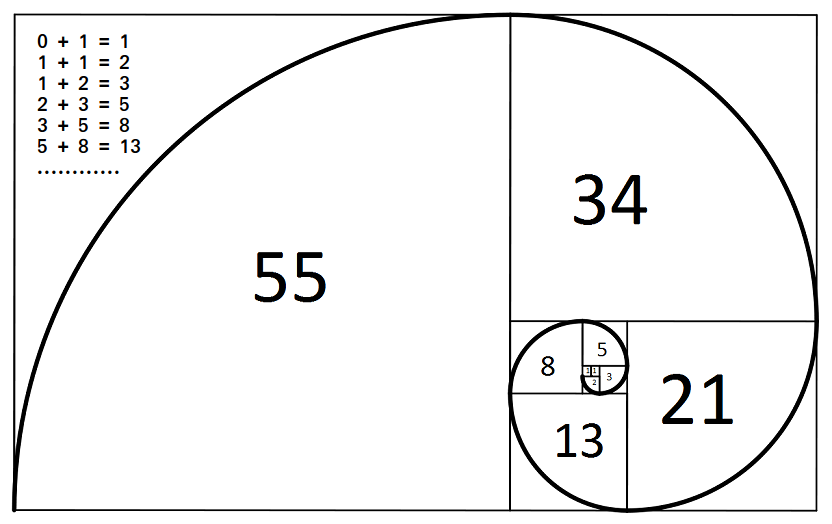
Print n-th fibonacci number
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ……..
n = 6
Problem #2
Stairs problem
You can climb 1 or 2 stairs with one sep. How many different ways can you climb n stairs ?
function stairs(n) {
// implement this
}Problem #3
Find max path if you can move down and right
(0, 0)
(x, y)
2
3
1
1
5
3
1
1
3
1
1
4
1
1
1
1
1
1
1
2
1
1
1
1
1
8
1
1
1
4
1
1
1
2
1
1
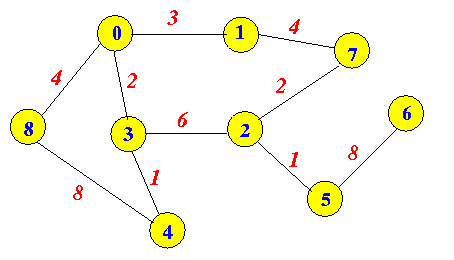
A weighted graph is a graph in which each branch is given a numerical weight. A weighted graph is therefore a special type of labeled graph in which the labels are numbers (which are usually taken to be positive)
But first lets refresh what is a Heap
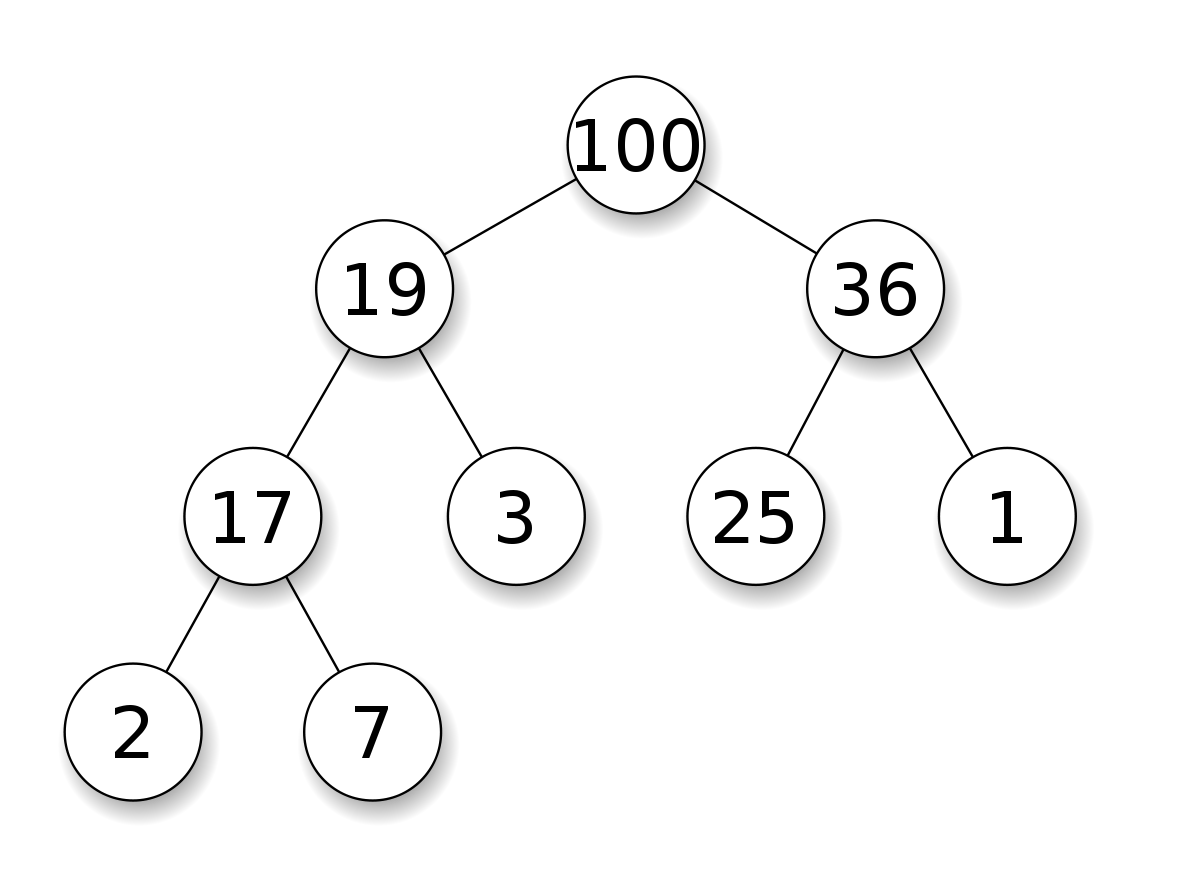
Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly.
What is a Heap ?
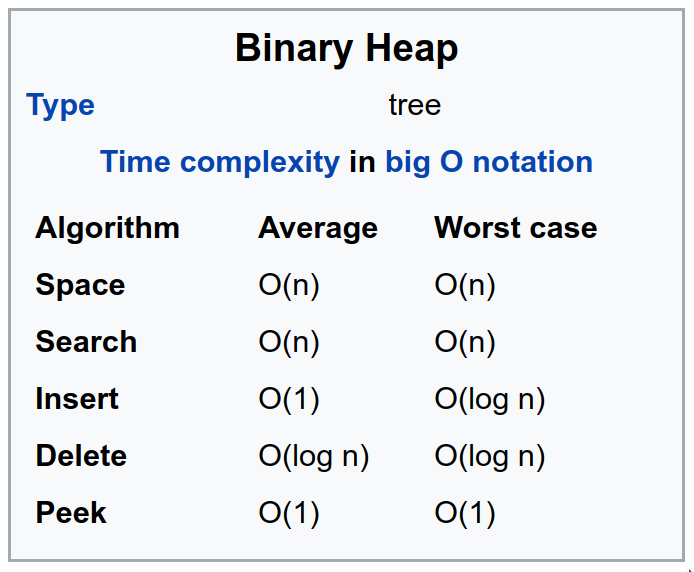
The complexity
function swap(arr, i, j) {
const temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
class Heap {
constructor() {
this.data = [];
this.size = 0;
}
bubbleUp(index = this.size - 1) {
const parentIndex = Math.floor((index - 1) / 2);
if (this.data[index] > this.data[parentIndex]) {
swap(this.data, index, parentIndex);
this.bubbleUp(parentIndex);
}
}
push(val) { // instead of val we will have { label, prio } object
this.data.push(val);
this.size++;
this.bubbleUp();
}
maxHeapify(index = 0) {
let leftChildIndex = index * 2 + 1;
let rightChildIndex = index * 2 + 2;
let maxIndex = index;
if (leftChildIndex < this.size && this.data[leftChildIndex] > this.data[maxIndex]) {
maxIndex = leftChildIndex;
}
if (rightChildIndex < this.size && this.data[rightChildIndex] > this.data[maxIndex]) {
maxIndex = rightChildIndex;
}
if(maxIndex !== index){
swap(this.data, maxIndex, index);
this.maxHeapify(maxIndex);
}
return this;
}
pop() {
const res = this.data[0];
const last = this.data.pop();
this.data[0] = last;
this.maxHeapify();
this.size--;
return res;
}
buildMaxHeap(arr = []) {
this.data = arr;
this.size = arr.length;
for(let i = Math.floor(this.size / 2); i >= 0; i--) {
this.maxHeapify(i);
}
return this;
}
print() { console.log(this.data) }
}
Refactor this to be a priority Queue
Dijkstra Algorithm
Example
Who the heck is Dijkstra
Edsger Wybe Dijkstra a Dutch systems scientist, programmer, software engineer, science essayist, and pioneer in computing science
(11 May 1930 – 6 August 2002)

- compiler construction,
- operating systems,
- concurrent programming , distributed programming,
- programming paradigm and methodology, programming language research,
- program design,
- program development,
- program verification,
- software engineering principles,
- algorithm design,
- and philosophical foundations of computer programming and computer science
Dijkstra made numerous seminal contributions to many areas of computing science:
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph
How to find a shortest path A -> C ?
A
B
C
D
100
1
1
1


We need a table with shotest paths
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | Inf |
| C | Inf |
| D | Inf |
Distances from A
Then we start to iterate over adjacency list of A
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | Inf |
| C | Inf |
| D | Inf |
Distances from A
Is it smaller than our table info ?
Yes!
100
Lets also store how did we come to the current node!
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | 100 |
| C | Inf |
| D | Inf |
Distances from A
| A | null |
|---|---|
| B | A |
| C | null |
| D | null |
Previos chain
Continue iterating adjacency list of A
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | 100 |
| C | Inf |
| D | Inf |
Distances from A
| A | null |
|---|---|
| B | A |
| C | null |
| D | null |
Previos chain
Dist to D = weight + dist to A
1 + 0 = 1
Is it smaller then dist from table ?
Yes
1
How did we come to D ?
through A!
A
Continue iterating
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | 100 |
| C | Inf |
| D | 1 |
Distances from A
| A | null |
|---|---|
| B | A |
| C | null |
| D | A |
Previos chain
B
D
We've alread been on
Pull adjacency list of B!
Continue iterating from B
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | 100 |
| C | Inf |
| D | 1 |
Distances from A
| A | null |
|---|---|
| B | A |
| C | null |
| D | A |
Previos chain
Dist = 1 + 100
Replace its in tables !
101
B
Continue iterating from D
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | 100 |
| C | 101 |
| D | 1 |
Distances from A
| A | null |
|---|---|
| B | A |
| C | B |
| D | A |
Previos chain
Dist = 1 + 1
Is 2 < 101 ???
Yes!
Rewrite values in tables !
D
2
Analizing tables
A
B
C
D
100
1
1
1
| A | 0 |
|---|---|
| B | 100 |
| C | 2 |
| D | 1 |
Distances from A
| A | null |
|---|---|
| B | A |
| C | D |
| D | A |
Previos chain
The shortest path from A to C = 2
But how did we get to C ?
Through D!
But how did we get to D ?
Through A!
Dijkstra high level
algorithm steps
-
Define a methed with two arguments: from, to
-
Define variables which will hold: table of distances, table of previous nodes, and priority queue of next nodes
-
Init prev map with null, and distance map with Infinity except start node (shoud have 0). Add all adjacency nodes from node to priority queue
-
Pop items from the queue while length > 0
-
Iterate over current (popped) item adjacency list
-
Calculate distance using table + weight
-
If candidate distance is smaller then table record - override it and enqueue all neighbours of current node
-
After the the queue is empty - calculate the path using table of distances and table of previous nodes


Dijkstra's algorithm. It picks the unvisited vertex with the lowest-distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller. Mark visited (set to red) when done with neighbors.
Lets try
to implement it!
class PriorityQueue {
constructor() {
this.data = []
}
enqueue(value, prio) {
this.data.push({ value, prio });
this.data.sort((v1, v2) => v1.prio - v2.prio);
}
dequeue() {
return this.data.shift();
}
}
class WeightedGraph {
constructor() {
this.adjacencyList = {};
}
addVertex(node) {
this.adjacencyList[node] = [];
return this;
}
addEdge(vrt1, vrt2, weight) {
if(this.adjacencyList[vrt1] && this.adjacencyList[vrt2]) {
this.adjacencyList[vrt1].push({ node: vrt2, weight });
this.adjacencyList[vrt2].push({ node: vrt1, weight });
}
return this;
}
dfs(from = 'A') {
const visited = { [from]: true };
const res = [];
const stack = [ from ];
while(stack.length > 0) {
const curr = stack.pop();
res.push(curr);
this.adjacencyList[curr].forEach(edge => {
if (!visited[edge.node]) {
visited[edge.node] = true;
stack.push(edge.node);
}
})
}
return res;
}
shortestPath(from, to) {
// 1 declare variables
// distance, prev, queue
// 2 init
// for reach node in adjacencyList
// count set it distance to 0 if its a starting node or Infinity in other case
// set dist map
// set prev to null
// enqueue node to PriorityQueue
// 3 iterate over queue
// pop curr item
// iterate over curr adjacencylist
// count dist using table + weight
// if dist < than existing intable - override it
// 4 calc path using prev nodes table
}
}
const weightedGraph = new WeightedGraph();
/*
A -- 100 -- B -- 1 -- C
\ /
1 1
\ /
D
*/
weightedGraph
.addVertex('A')
.addVertex('B')
.addVertex('C')
.addVertex('D')
.addEdge('A', 'B', 100)
.addEdge('B', 'C', 1)
.addEdge('A', 'D', 1)
.addEdge('D', 'B', 1);
console.log(weightedGraph.shortestPath('A', 'C'));

Thank you!
Algorithms #12
By Vladimir Vyshko
Algorithms #12
Dijkstra algorithm
- 705



